6.1 平方根 第3课时 课件 (共19张PPT)
文档属性
| 名称 | 6.1 平方根 第3课时 课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 18:14:34 | ||
图片预览






文档简介
(共19张PPT)
第6.1平方根第3课时
人教版数学七年级下册
学习目标
1.掌握平方根的意义及性质.
2.理解平方根与算术平方根的联系与区别.
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有,请求出它们的算术平方根.
100;1; ; 0;-0.0025;(-3)2 ;-25;
10 1 0 无 3 无
复习引入
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根.
互动新授
思考 如果一个数的平方等于9,这个数是多少?
从前面我们知道,这个数可以是3.
除了3以外,还有没有别的数的平方也等于9呢?
由于(-3)2=9,这个数也可以是-3.
因此,如果一个数的平方等于9,那么这个数是3或-3.
互动新授
根据上面的研究过程填表:
x2 1 16 36 49
x
±1
±4
±6
±7
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.这就是说,使得x2=a,那么x叫做a的平方根.
互动新授
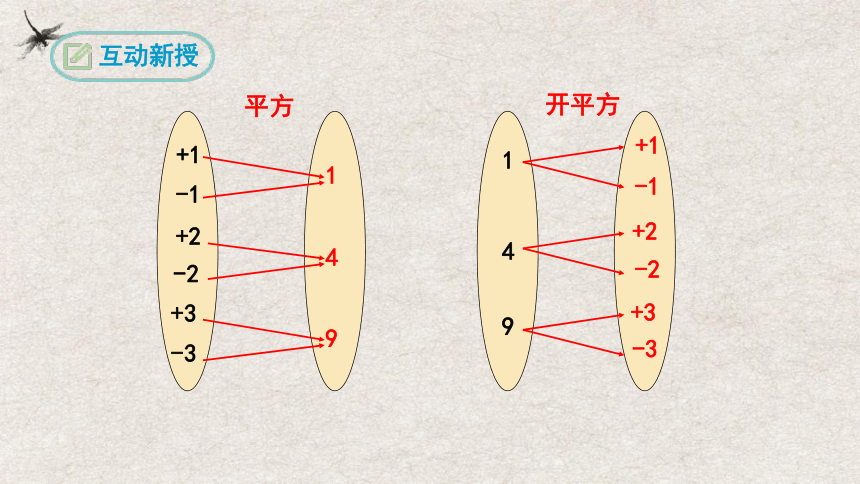
例如,3和-3是9的平方根,简记为±3是9的平方根.
求一个数a的平方根的运算,叫做开平方.
我们看到,±3的平方等于9,9的平方根是±3,所以平方与开平方互为逆运算,根据这种互逆关系,可以求一个数的平方根.
互动新授
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
典例精析
例4 求下列各数的平方根:
(1)100; (2) ; (3)0.25.
解:(1)因为(±10)2=100,所以100的平方根是±10;
(2)因为 ,所以 的平方根是 ;
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
互动新授
思考
正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.
因为02=0,并且任何一个不为0的数的平方都不等于0,所以0的平方根是0.
正数的平方是正数,0的平方是0,负数的平方也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
互动新授
归纳:
正数的平方根有两个,它们互为相反数;
0的平方根是0;
负数没有平方根.
我们知道,正数a的算术平方根可以用 表示;正数a的负的平方根,可以用符号“ ”表示,故正数a的平方根可以用符号“ ”表示,读作“正、负根号a”.
例如, .
典例精析
例5 求下列各式的值:
(1) ; (2) ; (3) .
解:(1)因为62=36,所以 ;
(2)因为0.92=0.81,所以 ;
(3)因为 ,所以 .
1.判断下列说法是否正确.
正确.
(4)(-4)2的平方根是-4.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
正确.
不正确,是 4.
不正确,是 ±4.
小试牛刀
1.若一个正数的平方根为和,则( )
A.7 B.16 C.25 D.49
D
2.已知,且,则的值为( )
A. B.C.或 D.或-2
C
课堂检测
4.下列说法不正确的是______
A.0的平方根是0
B.-22的平方根是2
C.非负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
3.下列说法正确的是_________
①-3是9的平方根;②25的平方根是5;③-36的平方根是-6;④平方根等于0的数是0;⑤64的算术平方根是8.
①④⑤
B
课堂检测
1.如果一个数的两个平方根时a+3,2a-15,那么这个数是多少?
解:因为一个数正数的两个平方根互为相反数,
所以(a+3)+(2a-15)=0,
解得a=4,
当a=4时,a+3=7,2a-15=-7.
即这个数是49.
拓展训练
平方根的性质
平方根的概念
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
开平方及相关运算
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.a﹙a≥0﹚的平方根表示为 .
课堂小结
1.下列各式中,正确的是( )
A. B.
C. D.
B
课后作业
2.判断下列说法是否正确:
(1)9的平方根是-3; ( )
(2)4的平方根是±2;( )
(3)若x2=16,则x=4;( )
(4)5是25的平方根; ( )
(5)25的平方根是5. ( )
×
√
×
×
√
课后作业
谢谢聆听
第6.1平方根第3课时
人教版数学七年级下册
学习目标
1.掌握平方根的意义及性质.
2.理解平方根与算术平方根的联系与区别.
1.什么叫做算术平方根?
2.判断下列各数有没有算术平方根,如果有,请求出它们的算术平方根.
100;1; ; 0;-0.0025;(-3)2 ;-25;
10 1 0 无 3 无
复习引入
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根.
互动新授
思考 如果一个数的平方等于9,这个数是多少?
从前面我们知道,这个数可以是3.
除了3以外,还有没有别的数的平方也等于9呢?
由于(-3)2=9,这个数也可以是-3.
因此,如果一个数的平方等于9,那么这个数是3或-3.
互动新授
根据上面的研究过程填表:
x2 1 16 36 49
x
±1
±4
±6
±7
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.这就是说,使得x2=a,那么x叫做a的平方根.
互动新授
例如,3和-3是9的平方根,简记为±3是9的平方根.
求一个数a的平方根的运算,叫做开平方.
我们看到,±3的平方等于9,9的平方根是±3,所以平方与开平方互为逆运算,根据这种互逆关系,可以求一个数的平方根.
互动新授
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
典例精析
例4 求下列各数的平方根:
(1)100; (2) ; (3)0.25.
解:(1)因为(±10)2=100,所以100的平方根是±10;
(2)因为 ,所以 的平方根是 ;
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
互动新授
思考
正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.
因为02=0,并且任何一个不为0的数的平方都不等于0,所以0的平方根是0.
正数的平方是正数,0的平方是0,负数的平方也是正数,即在我们所认识的数中,任何一个数的平方都不会是负数,所以负数没有平方根.
互动新授
归纳:
正数的平方根有两个,它们互为相反数;
0的平方根是0;
负数没有平方根.
我们知道,正数a的算术平方根可以用 表示;正数a的负的平方根,可以用符号“ ”表示,故正数a的平方根可以用符号“ ”表示,读作“正、负根号a”.
例如, .
典例精析
例5 求下列各式的值:
(1) ; (2) ; (3) .
解:(1)因为62=36,所以 ;
(2)因为0.92=0.81,所以 ;
(3)因为 ,所以 .
1.判断下列说法是否正确.
正确.
(4)(-4)2的平方根是-4.
(1) 是 的一个平方根;
(2) 是6的算术平方根;
(3) 的值是±4;
正确.
不正确,是 4.
不正确,是 ±4.
小试牛刀
1.若一个正数的平方根为和,则( )
A.7 B.16 C.25 D.49
D
2.已知,且,则的值为( )
A. B.C.或 D.或-2
C
课堂检测
4.下列说法不正确的是______
A.0的平方根是0
B.-22的平方根是2
C.非负数的平方根互为相反数
D.一个正数的算术平方根一定大于这个数的相反数
3.下列说法正确的是_________
①-3是9的平方根;②25的平方根是5;③-36的平方根是-6;④平方根等于0的数是0;⑤64的算术平方根是8.
①④⑤
B
课堂检测
1.如果一个数的两个平方根时a+3,2a-15,那么这个数是多少?
解:因为一个数正数的两个平方根互为相反数,
所以(a+3)+(2a-15)=0,
解得a=4,
当a=4时,a+3=7,2a-15=-7.
即这个数是49.
拓展训练
平方根的性质
平方根的概念
正数有两个平方根,两个平方根互为相反数;0的平方根是0;
负数没有平方根.
开平方及相关运算
一般地,如果一个数的平方等于a,那么这个数叫作a的平方根或二次方根.a﹙a≥0﹚的平方根表示为 .
课堂小结
1.下列各式中,正确的是( )
A. B.
C. D.
B
课后作业
2.判断下列说法是否正确:
(1)9的平方根是-3; ( )
(2)4的平方根是±2;( )
(3)若x2=16,则x=4;( )
(4)5是25的平方根; ( )
(5)25的平方根是5. ( )
×
√
×
×
√
课后作业
谢谢聆听
