6.3 实数 课件 (共25张PPT)
图片预览







文档简介
(共25张PPT)
第6.3 实数
人教版数学七年级下册
学习目标
1.理解无理数和实数的概念.
2.对实数进行分类,判断一个数是有理数还是无理数.
3.理解实数和数轴上的点一一对应.
4.掌握实数的运算法则及运算律.
探究
我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
,- .
情境引入
=2.5 ,-
=1.2
= 0.81818181… =0.81
互动新授
我们发现,上面的分数都可以写成有限小数或无限循环小数形式.
事实上,如果把整数看成小数点后是0的小数(例如,将3看成3.0),那么任何一个有理数都可以写成有限小数或无限循环小数的形式.
反过来,任何有限小数和无限循环小数也都是有理数.
互动新授
通过前两节的学习,我们知道,很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫做无理数.
例如 等都是无理数,π=3.14159265…也是无理数.
像有理数一样,无理数也有正负之分.例如, ,π 是正无理数, ,-π是负无理数.
互动新授
有理数和无理数统称为实数.
0
正有理数
正无理数
负有理数
负无理数
实数
有理数
无理数
有限小数或无限循环小数
无限不循环小数
互动新授
实数也有正负之分,所以实数还可以按大小分类如下:
0
正实数
负实数
实数
我们知道,每个有理数都可以用数轴上的点来表示.无理数是否也可以用数轴上的点表示出来呢?
互动新授
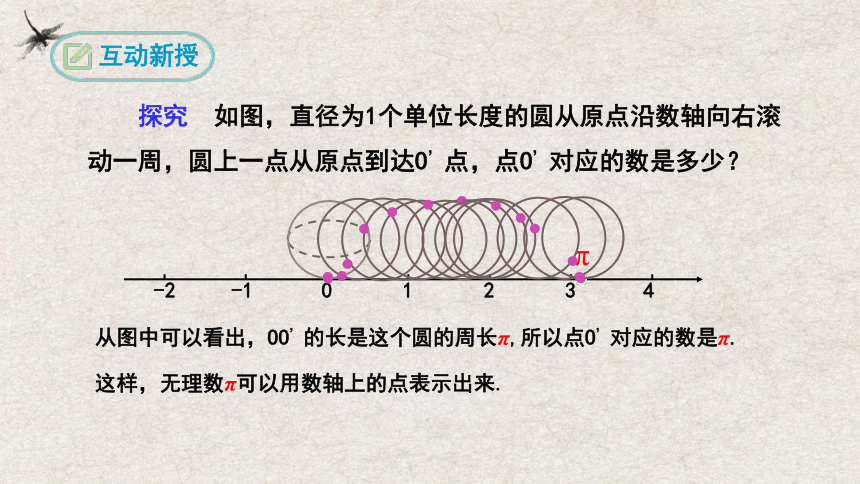
探究 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O’点,点O’对应的数是多少?
●
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
从图中可以看出,OO’的长是这个圆的周长π,所以点O’对应的数是π.
这样,无理数π可以用数轴上的点表示出来.
互动新授
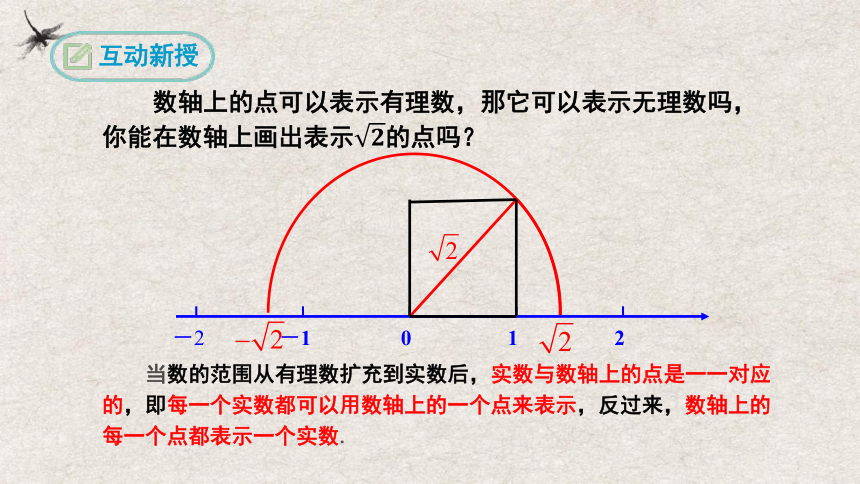
数轴上的点可以表示有理数,那它可以表示无理数吗,你能在数轴上画出表示的点吗?
-2
-1
0
1
2
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数.
互动新授
思考
(1)的相反数为_____,-π的相反数是_____,0的相反数是________;
(2)||=________,|-π|=________,|0|=________.
有理数中的相反数、绝对值、倒数等概念对实数仍然适用.
π
π
0
0
相反数性质:
绝对值性质:
数a的相反数是-a,这里a可取任意实数.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
假设a表示一个实数,即
(a>0)
|a|= (a=0)
(a<0)
a
0
-a
互动新授
典例精析
例1 (1)分别写出π-3.14的相反数;
(2)指出分别是什么数的相反数;
(3)求的绝对值;
(4)已知一个数的绝对值是,求这个数.
解:(1)因为 ,-(π-3.14)=3.14-π,
所以, ,π-3.14的相反数分别为 ,3.14-π.
(2)因为 ,
所以, 分别是 的相反数.
典例精析
(3)因为 ,
所以 .
(4)因为 ,
所以绝对值为 的数是 或 .
典例精析
例2 计算下列各式的值:
典例精析
例3 计算(结果保留小数点后两位):
解:
1.下列说法正确的是( )
A.a一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
小试牛刀
无理数:
有理数:
负实数:
正实数:
2.将下列各数分别填入下列相应的括号内:
小试牛刀
1.判断
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
8.数轴上的任何一点都可以表示实数.( )
×
×
×
课堂检测
1.下列说法正确的是( )
A.a一定是正实数 B.是有理数
C.是有理数 D.数轴上任一点都对应一个有理数
B
2.估计 位于( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
B
课堂检测
1.有一个数值转换器,原理如下,当输x=81时,输出的y是( )
输入x
取算术平方根
是无理数
输出y
是有理数
A.9 B.3 C. D.±3
C
拓展训练
2.如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心、正方形对角线的长为半径画弧,交数轴于点A,则点A表示的数是( )
A.- B.2- C.1- D.1+
B
拓展训练
有理数和无理数统称为实数.
课堂小结
实数的分类:
相反数性质:
绝对值性质:
数a的相反数是-a,这里a可取任意实数.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
假设a表示一个实数,即
(a>0)
|a|= (a=0)
(a<0)
a
0
-a
1.判断:
(1) ( )
(2) 的绝对值是 ; ( )
(3) 的相反数是 . ( )
×
×
课后作业
2.计算
(1)
(2)
(3)
=4
课后作业
谢谢聆听
第6.3 实数
人教版数学七年级下册
学习目标
1.理解无理数和实数的概念.
2.对实数进行分类,判断一个数是有理数还是无理数.
3.理解实数和数轴上的点一一对应.
4.掌握实数的运算法则及运算律.
探究
我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
,- .
情境引入
=2.5 ,-
=1.2
= 0.81818181… =0.81
互动新授
我们发现,上面的分数都可以写成有限小数或无限循环小数形式.
事实上,如果把整数看成小数点后是0的小数(例如,将3看成3.0),那么任何一个有理数都可以写成有限小数或无限循环小数的形式.
反过来,任何有限小数和无限循环小数也都是有理数.
互动新授
通过前两节的学习,我们知道,很多数的平方根和立方根都是无限不循环小数,无限不循环小数又叫做无理数.
例如 等都是无理数,π=3.14159265…也是无理数.
像有理数一样,无理数也有正负之分.例如, ,π 是正无理数, ,-π是负无理数.
互动新授
有理数和无理数统称为实数.
0
正有理数
正无理数
负有理数
负无理数
实数
有理数
无理数
有限小数或无限循环小数
无限不循环小数
互动新授
实数也有正负之分,所以实数还可以按大小分类如下:
0
正实数
负实数
实数
我们知道,每个有理数都可以用数轴上的点来表示.无理数是否也可以用数轴上的点表示出来呢?
互动新授
探究 如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上一点从原点到达O’点,点O’对应的数是多少?
●
0
-2
-1
1
3
2
4
●
●
●
●
●
●
●
●
●
●
●
●
●
从图中可以看出,OO’的长是这个圆的周长π,所以点O’对应的数是π.
这样,无理数π可以用数轴上的点表示出来.
互动新授
数轴上的点可以表示有理数,那它可以表示无理数吗,你能在数轴上画出表示的点吗?
-2
-1
0
1
2
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数.
互动新授
思考
(1)的相反数为_____,-π的相反数是_____,0的相反数是________;
(2)||=________,|-π|=________,|0|=________.
有理数中的相反数、绝对值、倒数等概念对实数仍然适用.
π
π
0
0
相反数性质:
绝对值性质:
数a的相反数是-a,这里a可取任意实数.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
假设a表示一个实数,即
(a>0)
|a|= (a=0)
(a<0)
a
0
-a
互动新授
典例精析
例1 (1)分别写出π-3.14的相反数;
(2)指出分别是什么数的相反数;
(3)求的绝对值;
(4)已知一个数的绝对值是,求这个数.
解:(1)因为 ,-(π-3.14)=3.14-π,
所以, ,π-3.14的相反数分别为 ,3.14-π.
(2)因为 ,
所以, 分别是 的相反数.
典例精析
(3)因为 ,
所以 .
(4)因为 ,
所以绝对值为 的数是 或 .
典例精析
例2 计算下列各式的值:
典例精析
例3 计算(结果保留小数点后两位):
解:
1.下列说法正确的是( )
A.a一定是正实数
B. 是有理数
C. 是有理数
D.数轴上任一点都对应一个有理数
B
小试牛刀
无理数:
有理数:
负实数:
正实数:
2.将下列各数分别填入下列相应的括号内:
小试牛刀
1.判断
1.实数不是有理数就是无理数.( )
2.无理数都是无限不循环小数.( )
3.无理数都是无限小数.( )
4.带根号的数都是无理数.( )
5.无理数一定都带根号.( )
6.两个无理数之积不一定是无理数.( )
7.两个无理数之和一定是无理数.( )
8.数轴上的任何一点都可以表示实数.( )
×
×
×
课堂检测
1.下列说法正确的是( )
A.a一定是正实数 B.是有理数
C.是有理数 D.数轴上任一点都对应一个有理数
B
2.估计 位于( )
A.0~1之间 B.1~2之间
C.2~3之间 D.3~4之间
B
课堂检测
1.有一个数值转换器,原理如下,当输x=81时,输出的y是( )
输入x
取算术平方根
是无理数
输出y
是有理数
A.9 B.3 C. D.±3
C
拓展训练
2.如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心、正方形对角线的长为半径画弧,交数轴于点A,则点A表示的数是( )
A.- B.2- C.1- D.1+
B
拓展训练
有理数和无理数统称为实数.
课堂小结
实数的分类:
相反数性质:
绝对值性质:
数a的相反数是-a,这里a可取任意实数.
正数的绝对值是它本身;
负数的绝对值是它的相反数;
0的绝对值是0.
假设a表示一个实数,即
(a>0)
|a|= (a=0)
(a<0)
a
0
-a
1.判断:
(1) ( )
(2) 的绝对值是 ; ( )
(3) 的相反数是 . ( )
×
×
课后作业
2.计算
(1)
(2)
(3)
=4
课后作业
谢谢聆听
