2022-2023学年山东省青岛市黄岛区、胶州市八年级(上)期末数学试卷(word,解析版)
文档属性
| 名称 | 2022-2023学年山东省青岛市黄岛区、胶州市八年级(上)期末数学试卷(word,解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 657.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 08:07:35 | ||
图片预览




文档简介
2022-2023学年山东省青岛市黄岛区、胶州市八年级(上)期末数学试卷
一、选择题(本大题共8小题,每小题3分,共24分)在每个题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)的绝对值是( )
A. B. C.5 D.﹣5
2.(3分)将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
3.(3分)青岛火车站是一座百年老站,是青岛市的标志性建筑之一.下列能准确表示青岛火车站地理位置的是( )
A.山东省青岛市
B.青岛市市南区泰安路2号
C.栈桥风景区的西北方向
D.胶州湾隧道口大约2千米处
4.(3分)要说明命题“若|a|>5,则a>5”是假命题,可以举的一个反例是( )
A.a=5 B.a=﹣5 C.a=6 D.a=﹣6
5.(3分)小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
6.(3分)如图是一个“数值转换机”的示意图,当输入81时,输出的值是( )
A. B.3 C.3 D.9
7.(3分)已知直线y=3x与y=﹣2x+b的交点的坐标为(1,a),则a+b的值为( )
A.2 B.4 C.8 D.15
8.(3分)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是( )
A.(2022,0) B.(2023,0) C.(2023,2) D.(2023,﹣2)
二、填空题(本大题共8小题,每小题3分,共24分)
9.(3分)写一个大于2且小于3的无理数 .
10.(3分)为参加校运会,小强同学进行立定跳远训练,其中6次的成绩如下(单位:m):2.2,2.6,2.4,2.5,2.4,2.4.这6次成绩的极差是 m.
11.(3分)某校规定:学生的平时测试、期中测试、期末测试三项成绩分别按20%,40%,40%的比例计入学期总评成绩.小明的平时测试、期中测试、期末测试的体育成绩依次为90分,90分,95分,则小明这学期的体育总评成绩为 分.
12.(3分)若是二元一次方程ax+by=﹣2的一个解,则3a﹣2b+2024的值为 .
13.(3分)现规定一种运算:a※b=ab+a﹣b,其中a,b为实数.例如:1※(﹣5)=1×(﹣5)+1﹣(﹣5)=1,则※的值为 .
14.(3分)两个两位数的差是18,在较大的两位数的右边接着写上较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.若这两个四位数的和是6666,这两个两位数分别是多少?设较大的两位数为x,较小的两位数为y,根据题意列出的方程组为 .
15.(3分)请写出一个满足条件①②的一次函数关系式y= .
①图象不经过第一象限,且与y轴交于负半轴;
②当x=﹣3时,y=0.
16.(3分)如图是某滑雪场U型池的示意图,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半圆,其边缘AB=CD=16,点E在CD上,CE=4.一名滑雪爱好者从A点滑到E点时,他滑行的最短路程约为 (π取3).
三、作图题(本题满分4分)
17.(4分)已知:△ABC.
求作:直线AD,使得AD∥BC.
四、解答题(本大题共8小题,共68分)
18.(8分)(1)计算:﹣;
(2)计算:(2+)(2﹣)﹣10.
19.(8分)(1)解方程组:;
(2)解方程组:.
20.(6分)有一张图纸被污染,上面只有如图所示的两个标志点A(﹣2,1),B(﹣3,﹣4)可识别.
请根据以上信息解答下列问题:
(1)在图中画出平面直角坐标系,并标出主要建筑C(3,2)的位置;
(2)标志点A与主要建筑C的图上距离为 .
21.(6分)如图,AB∥CD,直线EF分别与直线AB、直线CD相交于点E,F,点G在CD上,EG平分∠BEF.若∠EGC=58°,求∠EFD的度数.
22.(8分)为提高学生对计算机的兴趣,某校举办计算机汉字输入比赛.甲、乙两组各有10名学生参赛,两组学生每分钟输入汉字的个数如表:
输入汉字(个) 132 133 134 135 136 137
甲组人数(人) 1 0 1 5 2 1
乙组人数(人) 0 1 4 1 2 2
(1)请将表中的相关数据补充完整:
组别 众数(个) 中位数(个) 平均数(个) 方差
甲组 135 135
乙组 134.5 1.8
(2)请根据所学的统计知识,从两个不同角度对甲、乙两组学生的比赛成绩进行分析.
23.(10分)小明和小亮两人各带20元钱同时到一家文具店购买同一型号的中性笔和笔记本,这种中性笔每盒10支,如果整盒买比单支买每支可优惠0.2元.小明要买3支中性笔和4本笔记本,需花费19元;小亮要买7支中性笔和3本笔记本,需花费19元.
(1)求笔记本的单价和单独购买一支中性笔的价格;
(2)小明和小亮都还想再买一件单价为1.5元的小工艺品,他们利用所带的钱,能否做到既买全了想要的文具,又都能买到一件小工艺品?请通过计算说明.
24.(10分)【课本再现】
已知:如图1,P是三角形ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明:如图2,延长BP,交AC于点 D.
∵∠BPC是△PCD的一个外角(外角的定义),
∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角).
∵∠PDC是△ABD的一个外角(外角的定义),
∴∠PDC>∠A(三角形的一个外角大于任何一个和它不相邻的内角).
∴∠BPC>∠A.
【知识迁移】
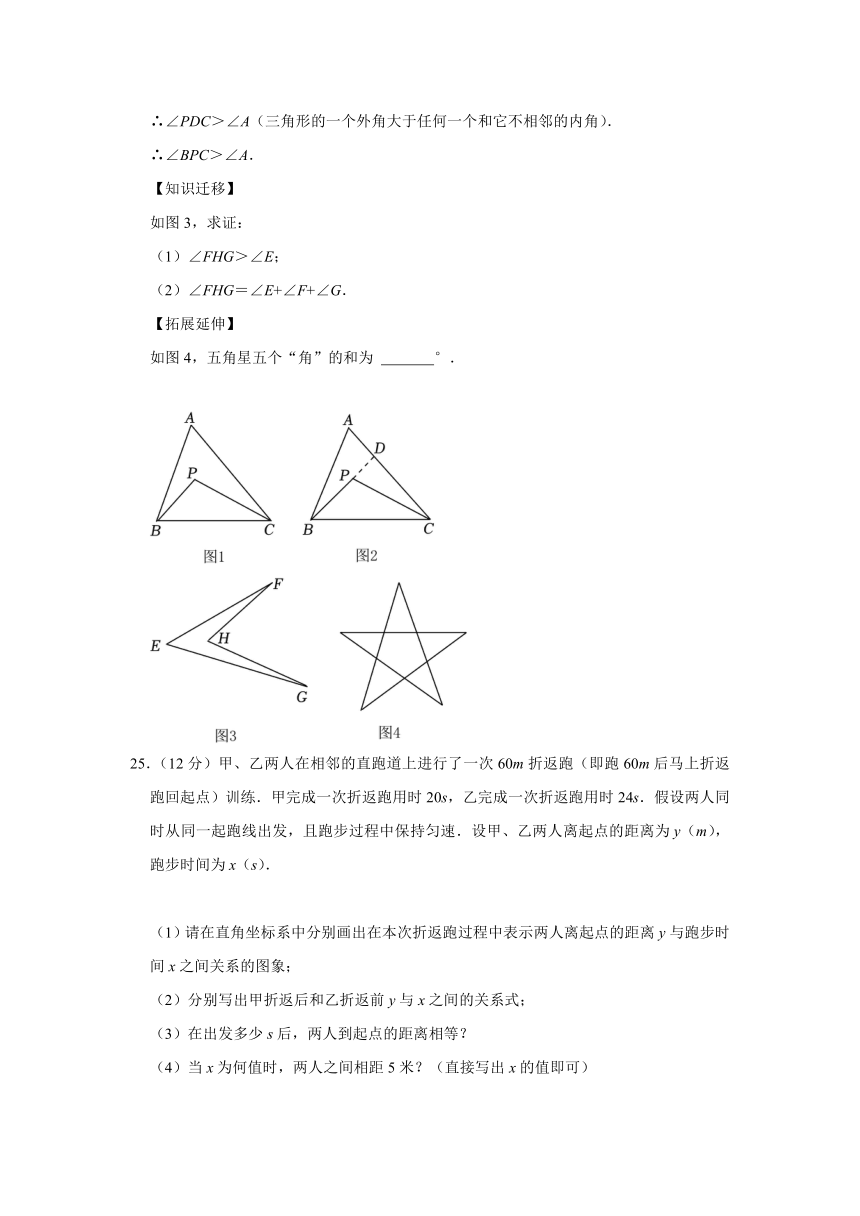
如图3,求证:
(1)∠FHG>∠E;
(2)∠FHG=∠E+∠F+∠G.
【拓展延伸】
如图4,五角星五个“角”的和为 °.
25.(12分)甲、乙两人在相邻的直跑道上进行了一次60m折返跑(即跑60m后马上折返跑回起点)训练.甲完成一次折返跑用时20s,乙完成一次折返跑用时24s.假设两人同时从同一起跑线出发,且跑步过程中保持匀速.设甲、乙两人离起点的距离为y(m),跑步时间为x(s).
(1)请在直角坐标系中分别画出在本次折返跑过程中表示两人离起点的距离y与跑步时间x之间关系的图象;
(2)分别写出甲折返后和乙折返前y与x之间的关系式;
(3)在出发多少s后,两人到起点的距离相等?
(4)当x为何值时,两人之间相距5米?(直接写出x的值即可)
2022-2023学年山东省青岛市黄岛区、胶州市八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题3分,共24分)在每个题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)的绝对值是( )
A. B. C.5 D.﹣5
【分析】根据绝对值的概念得出结论即可.
【解答】解:﹣的绝对值是,
故选:A.
2.(3分)将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
【分析】根据勾股定理得出a2+b2=c2,推出100a2+100b2=100c2,得出(10a)2+(10b)2=(10c)2,根据勾股定理的逆定理得出即可.
【解答】解:如图,设直角三角形ABC的三边的长是a、b、c,则a2+b2=c2,
∴100a2+100b2=100c2,
即(10a)2+(10b)2=(10c)2,
∴将一个直角三角形的三边长同时扩大10倍,得到的三角形是直角三角形,
故选:C.
3.(3分)青岛火车站是一座百年老站,是青岛市的标志性建筑之一.下列能准确表示青岛火车站地理位置的是( )
A.山东省青岛市
B.青岛市市南区泰安路2号
C.栈桥风景区的西北方向
D.胶州湾隧道口大约2千米处
【分析】根据坐标确定位置的方法,结合具体的情景进行判断即可.
【解答】解:根据坐标确定位置的方法可知,
A.山东省青岛市,只是确定了一个范围,不是一个具体的点,因此选项A不符合题意;
B.青岛市市南区泰安路2号,确定了点的位置,因此选项B符合题意;
C.栈桥风景区的西北方向,具体位置不确定,无法确定青岛火车站的位置,因此选项C不符合题意;
D.胶州湾隧道口大约2千米处,只是确定一个范围,不能确定火车站的具体的位置点,因此选项D不符合题意;
故选:B.
4.(3分)要说明命题“若|a|>5,则a>5”是假命题,可以举的一个反例是( )
A.a=5 B.a=﹣5 C.a=6 D.a=﹣6
【分析】举的反例是满足条件,但不能得到结论,据此可得答案.
【解答】解:a=﹣6时,满足|a|>5,但﹣6<5,
故选:D.
5.(3分)小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
【分析】根据中位数定义可得答案.
【解答】解:中位数与计算结果与被涂污数字无关,
故选:D.
6.(3分)如图是一个“数值转换机”的示意图,当输入81时,输出的值是( )
A. B.3 C.3 D.9
【分析】理解“数值转换机”的示意图,代入求值即可.
【解答】解:根据题意有,输出的值为:.
故选:A.
7.(3分)已知直线y=3x与y=﹣2x+b的交点的坐标为(1,a),则a+b的值为( )
A.2 B.4 C.8 D.15
【分析】根据直线y=3x与y=﹣2x+b的交点的坐标为(1,a),先求出a的值,再待定系数法求出b的值,进一步求解即可.
【解答】解:∵直线y=3x与y=﹣2x+b的交点的坐标为(1,a),
∴a=3×1=3,
将点(1,3)代入y=﹣2x+b,
得﹣2+b=3,
解得b=5,
∴a+b=3+5=8,
故选:C.
8.(3分)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是( )
A.(2022,0) B.(2023,0) C.(2023,2) D.(2023,﹣2)
【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,继而求得答案.
【解答】解:观察图形可知,
点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,
2023÷4=505……3,
所以点A2023坐标是(2023,2).
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)
9.(3分)写一个大于2且小于3的无理数 (答案不唯一) .
【分析】根据算术平方根的性质可以把2和3写成带根号的形式,再进一步写出一个被开方数介于两者之间的数即可.
【解答】解:∵2=,3=,
∴写出一个大于2小于3的无理数是、等.
故答案为:(答案不唯一).
10.(3分)为参加校运会,小强同学进行立定跳远训练,其中6次的成绩如下(单位:m):2.2,2.6,2.4,2.5,2.4,2.4.这6次成绩的极差是 0.4 m.
【分析】根据极差的定义求解即可.
【解答】解:这组数据的极差为2.6﹣2.2=0.4m,
故答案为:0.4.
11.(3分)某校规定:学生的平时测试、期中测试、期末测试三项成绩分别按20%,40%,40%的比例计入学期总评成绩.小明的平时测试、期中测试、期末测试的体育成绩依次为90分,90分,95分,则小明这学期的体育总评成绩为 92 分.
【分析】这学期总评成绩是平时测试、期中测试、期末测试的体育成绩与其对应百分比的乘积之和.
【解答】解:小明这学期总评成绩=90×20%+90×40%+95×40%=36+18.4+34=92(分).
故答案为:92.
12.(3分)若是二元一次方程ax+by=﹣2的一个解,则3a﹣2b+2024的值为 2022 .
【分析】把解代入二元一次方程中,把得到的等式和代数式整理变形,整体代入求值.
【解答】解:∵若是二元一次方程ax+by=﹣2的一个解,
∴3a﹣2b=﹣2,
∴3a﹣2b+2024
=﹣2+2024
=2022,
故答案为:2022.
13.(3分)现规定一种运算:a※b=ab+a﹣b,其中a,b为实数.例如:1※(﹣5)=1×(﹣5)+1﹣(﹣5)=1,则※的值为 ﹣1 .
【分析】读懂新定义,利用新定义计算.
【解答】解:※=2※(﹣3)=2×(﹣3)+2﹣(﹣3)=﹣6+2+3=﹣1,
故答案为:﹣1.
14.(3分)两个两位数的差是18,在较大的两位数的右边接着写上较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.若这两个四位数的和是6666,这两个两位数分别是多少?设较大的两位数为x,较小的两位数为y,根据题意列出的方程组为 .
【分析】首先设较大的两位数为x,较小的两位数为y,根据题意可得等量关系:①两个两位数的差是18,②100x+y与100y+x的和是6666,根据等量关系列出方程组即可.
【解答】解:设较大的两位数为x,较小的两位数为y,
根据题意,得.
故答案为:.
15.(3分)请写出一个满足条件①②的一次函数关系式y= ﹣x﹣3(答案不唯一) .
①图象不经过第一象限,且与y轴交于负半轴;
②当x=﹣3时,y=0.
【分析】设一次函数的关系式为y=kx+b(k≠0),由①,利用一次函数图象与系数的关系,可得出k<0,b<0,由②,利用一次函数图象上点的坐标特征,可求出b=3k,代入k=﹣1即可得出结论.
【解答】解:设一次函数的关系式为y=kx+b(k≠0),
∵该函数图象不经过第一象限,且与y轴交于负半轴,
∴k<0,b<0;
∵当x=﹣3时,y=0,
∴﹣3k+b=0,
∴b=3k.
当k=﹣1时,b=3k=3×(﹣1)=﹣3,
∴一次函数关系式可以为y=﹣x﹣3.
故答案为:﹣x﹣3(答案不唯一).
16.(3分)如图是某滑雪场U型池的示意图,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半圆,其边缘AB=CD=16,点E在CD上,CE=4.一名滑雪爱好者从A点滑到E点时,他滑行的最短路程约为 16 (π取3).
【分析】要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.
【解答】解:如图是其侧面展开图:AD=3×3=9,AB=CD=16.DE=CD﹣CE=16﹣4=12,
在Rt△ADE中,AE===16.
故他滑行的最短距离约为16.
故答案为:16.
三、作图题(本题满分4分)
17.(4分)已知:△ABC.
求作:直线AD,使得AD∥BC.
【分析】作∠DAC=∠C,则根据平行线的判定方法可判断AD∥BC.
【解答】解:如图,
四、解答题(本大题共8小题,共68分)
18.(8分)(1)计算:﹣;
(2)计算:(2+)(2﹣)﹣10.
【分析】(1)直接化简二次根式,进而计算得出答案;
(2)直接利用平方差公式化简,进而得出答案.
【解答】解:(1)原式=2﹣
=;
(2)原式=(2)2﹣()2﹣10
=12﹣2﹣10
=0.
19.(8分)(1)解方程组:;
(2)解方程组:.
【分析】(1)利用加减消元法进行求解即可;
(2)利用加减消元法进行求解即可.
【解答】解:(1),
①+②得:4m=12,
解得m=3,
把m=3代入②得:3+2n=5,
解得n=1,
故原方程组的解是:;
(2),
①×4得:4x﹣4y=4③,
②﹣③得:﹣y=﹣1,
解得y=1,
把y=1代入①得:x﹣1=1,
解得x=2,
故原方程组的解是:.
20.(6分)有一张图纸被污染,上面只有如图所示的两个标志点A(﹣2,1),B(﹣3,﹣4)可识别.
请根据以上信息解答下列问题:
(1)在图中画出平面直角坐标系,并标出主要建筑C(3,2)的位置;
(2)标志点A与主要建筑C的图上距离为 .
【分析】(1)根据点A(﹣2,1)确定x轴,y轴的位置,进而确定平面直角坐标系,再由点的坐标的定义确定点C的位置即可;
(2)根据网格构造直角三角形,利用勾股定理求出答案即可.
【解答】解:(1)画出平面直角坐标系,并标出主要建筑C(3,2)的位置如图所示:
(2)由网格构造直角三角形,由勾股定理得,
AC==,
故答案为:.
21.(6分)如图,AB∥CD,直线EF分别与直线AB、直线CD相交于点E,F,点G在CD上,EG平分∠BEF.若∠EGC=58°,求∠EFD的度数.
【分析】根据两直线平行,内错角相等求出∠BEG的度数,再根据角平分线的定义得到∠FEG,然后利用平行线的性质可得解.
【解答】解:∵AB∥CD,∠EGC=58°,
∴∠BEG=∠EGC=58°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=116°,
∵AB∥CD,
∴∠EFD=180°﹣∠BEF=180°﹣116°=64°.
22.(8分)为提高学生对计算机的兴趣,某校举办计算机汉字输入比赛.甲、乙两组各有10名学生参赛,两组学生每分钟输入汉字的个数如表:
输入汉字(个) 132 133 134 135 136 137
甲组人数(人) 1 0 1 5 2 1
乙组人数(人) 0 1 4 1 2 2
(1)请将表中的相关数据补充完整:
组别 众数(个) 中位数(个) 平均数(个) 方差
甲组 135 135 135 1.6
乙组 135 134.5 135 1.8
(2)请根据所学的统计知识,从两个不同角度对甲、乙两组学生的比赛成绩进行分析.
【分析】(1)根据众数、中位数、方差以及平均数的计算公式分别进行解答即可;
(2)从中位数看,甲组每分钟输入135字以上的人数比乙组多;从方差看,S2甲<S2乙;甲组成绩波动小,比较稳定.
【解答】解:(1)甲组的中位数是=135(个),
∵甲组的平均数是:×(132+134+135×5+136×2+137)=135(个),
∴甲的方差是:×[(132﹣135)2+(134﹣135)2+5×(135﹣135)2+2×(136﹣135)2+(137﹣135)2]=1.6,
乙组的众数为134(个),平均数为:×(133+134×4+135+136×2+137×2)=135(个),
补充完整如下:
组别 众数(个) 中位数(个) 平均数(个) 方差
甲组 135 135 135 1.6
乙组 134 134.5 135 1.8
(2)从中位数看,甲组每分钟输入135字以上的人数比乙组多,甲组成绩更好一些;
从方差看,S2甲<S2乙,甲组成绩波动小,比较稳定.
23.(10分)小明和小亮两人各带20元钱同时到一家文具店购买同一型号的中性笔和笔记本,这种中性笔每盒10支,如果整盒买比单支买每支可优惠0.2元.小明要买3支中性笔和4本笔记本,需花费19元;小亮要买7支中性笔和3本笔记本,需花费19元.
(1)求笔记本的单价和单独购买一支中性笔的价格;
(2)小明和小亮都还想再买一件单价为1.5元的小工艺品,他们利用所带的钱,能否做到既买全了想要的文具,又都能买到一件小工艺品?请通过计算说明.
【分析】(1)设单独购买一支中性笔的价格是x元,每本笔记本的单价是y元,依题意:小明要买3支中性笔和4本笔记本,需花费19元;小亮要买7支中性笔和3本笔记本,需花费19元.列出二元一次方程组,解方程组即可;
(2)若两人各自购买,则要买到想买的文具,小亮要花费19元,小明花费19元,则小明和小亮将无法再买一件小工艺品,若两人合在一起买文具,则买文具所需费用为36元,然后由40﹣36=4(元),1.5×2=3(元),即可得出结论.
【解答】解:(1)设单独购买一支中性笔的价格是x元,笔记本的单价是y元,
依题意得:,
解得:,
答:单独购买一支中性笔的价格是1元,笔记本的单价是4元.
(2)若两人各自购买,则要买到想买的文具,小亮要花费19元,小明花费19元,
∵小明和小亮每人有19元,
∴小明和小亮将无法再买一件小工艺品,
若两人合在一起买文具,则买文具所需费用为:(1﹣0.2)×(3+7)+4×(4+3)=36(元),
∵两人共有20+20=40(元),40﹣26=4(元),1.5×2=3(元),4﹣3=1(元),
∴两人应该合在一起买文具,才能既买到要买的文具又都能买到一件小工艺品.
24.(10分)【课本再现】
已知:如图1,P是三角形ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明:如图2,延长BP,交AC于点 D.
∵∠BPC是△PCD的一个外角(外角的定义),
∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角).
∵∠PDC是△ABD的一个外角(外角的定义),
∴∠PDC>∠A(三角形的一个外角大于任何一个和它不相邻的内角).
∴∠BPC>∠A.
【知识迁移】
如图3,求证:
(1)∠FHG>∠E;
(2)∠FHG=∠E+∠F+∠G.
【拓展延伸】
如图4,五角星五个“角”的和为 180 °.
【分析】(1)根据三角形的外角性质进行求解即可;
(2)利用三角形的外角性质进行解答即可;
【拓展延伸】利用三角形的外角性质即可求解.
【解答】(1)证明:延长GH交EF于点A,如图3,
∵∠FAH是△AEG的外角,
∴∠FAH>∠E,
∵∠FHG是△AFH的外角,
∴∠FHG>∠FAH,
∴∠FHG>∠E;
(2)证明∵∠FAH是△AEG的外角,
∴∠FAH=∠E+∠G,
∵∠FHG是△AFH的外角,
∴∠FHG=∠FAH+∠F,
∴∠FHG=∠E+∠F+∠G;
【拓展延伸】解:如图4,
∵∠FEG是△ABE的外角,∠FGE是△CDG的外角,
∴∠EFG=∠A+∠B,∠FGE=∠C+∠D,
∵∠F+∠EFG+∠FGE=180°,
∴∠F+∠A+∠B+∠C+∠D=180°.
故答案为:180.
25.(12分)甲、乙两人在相邻的直跑道上进行了一次60m折返跑(即跑60m后马上折返跑回起点)训练.甲完成一次折返跑用时20s,乙完成一次折返跑用时24s.假设两人同时从同一起跑线出发,且跑步过程中保持匀速.设甲、乙两人离起点的距离为y(m),跑步时间为x(s).
(1)请在直角坐标系中分别画出在本次折返跑过程中表示两人离起点的距离y与跑步时间x之间关系的图象;
(2)分别写出甲折返后和乙折返前y与x之间的关系式;
(3)在出发多少s后,两人到起点的距离相等?
(4)当x为何值时,两人之间相距5米?(直接写出x的值即可)
【分析】(1)根据题意画图即可;
(2)根据(1)中的图象求出其解析式即可;
(3)根据图象,求出直线交点的横坐标即可;
(4)分类讨论,分别求出x的值即可.
【解答】解:(1)如图所示:
(2)根据题意有,
甲折返后:在10<x≤20,甲的图象是直线函数,经过点(10,60)、(20,0),
设函数解析式为y=kx+b,将点(10,60)、(20,0)代入得,
,解得:,解析式为y=﹣6x+120,
∴甲折返后y与x之间的关系式为:y=﹣6x+120,(10<x≤20;
乙折返前:在0≤x<12,乙的图象是正比例函数,经过点(12,60),
设函数解析式为y=kx,将点(12,60)代入得,60=12k,解得:k=5,解析式为y=5x;
∴乙折返前y与x之间的关系式为:y=5x,(0≤x<12);
(3)当120﹣6x=5x时,解得:x=,
∴在出发s后,两人到起点的距离相等;
(4)①当6x﹣5x=5时,解得:x=5;
②120﹣6x﹣5x=5时,解得:x=;
③5x﹣(120﹣6x)=5时,解得:x=;
④当120﹣5x﹣(120﹣6x)=5时,解得:x=5,(不符合题意,舍去);
综上所述,当x=5或x=或x=时,两人之间相距5米.
一、选择题(本大题共8小题,每小题3分,共24分)在每个题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)的绝对值是( )
A. B. C.5 D.﹣5
2.(3分)将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
3.(3分)青岛火车站是一座百年老站,是青岛市的标志性建筑之一.下列能准确表示青岛火车站地理位置的是( )
A.山东省青岛市
B.青岛市市南区泰安路2号
C.栈桥风景区的西北方向
D.胶州湾隧道口大约2千米处
4.(3分)要说明命题“若|a|>5,则a>5”是假命题,可以举的一个反例是( )
A.a=5 B.a=﹣5 C.a=6 D.a=﹣6
5.(3分)小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
6.(3分)如图是一个“数值转换机”的示意图,当输入81时,输出的值是( )
A. B.3 C.3 D.9
7.(3分)已知直线y=3x与y=﹣2x+b的交点的坐标为(1,a),则a+b的值为( )
A.2 B.4 C.8 D.15
8.(3分)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是( )
A.(2022,0) B.(2023,0) C.(2023,2) D.(2023,﹣2)
二、填空题(本大题共8小题,每小题3分,共24分)
9.(3分)写一个大于2且小于3的无理数 .
10.(3分)为参加校运会,小强同学进行立定跳远训练,其中6次的成绩如下(单位:m):2.2,2.6,2.4,2.5,2.4,2.4.这6次成绩的极差是 m.
11.(3分)某校规定:学生的平时测试、期中测试、期末测试三项成绩分别按20%,40%,40%的比例计入学期总评成绩.小明的平时测试、期中测试、期末测试的体育成绩依次为90分,90分,95分,则小明这学期的体育总评成绩为 分.
12.(3分)若是二元一次方程ax+by=﹣2的一个解,则3a﹣2b+2024的值为 .
13.(3分)现规定一种运算:a※b=ab+a﹣b,其中a,b为实数.例如:1※(﹣5)=1×(﹣5)+1﹣(﹣5)=1,则※的值为 .
14.(3分)两个两位数的差是18,在较大的两位数的右边接着写上较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.若这两个四位数的和是6666,这两个两位数分别是多少?设较大的两位数为x,较小的两位数为y,根据题意列出的方程组为 .
15.(3分)请写出一个满足条件①②的一次函数关系式y= .
①图象不经过第一象限,且与y轴交于负半轴;
②当x=﹣3时,y=0.
16.(3分)如图是某滑雪场U型池的示意图,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半圆,其边缘AB=CD=16,点E在CD上,CE=4.一名滑雪爱好者从A点滑到E点时,他滑行的最短路程约为 (π取3).
三、作图题(本题满分4分)
17.(4分)已知:△ABC.
求作:直线AD,使得AD∥BC.
四、解答题(本大题共8小题,共68分)
18.(8分)(1)计算:﹣;
(2)计算:(2+)(2﹣)﹣10.
19.(8分)(1)解方程组:;
(2)解方程组:.
20.(6分)有一张图纸被污染,上面只有如图所示的两个标志点A(﹣2,1),B(﹣3,﹣4)可识别.
请根据以上信息解答下列问题:
(1)在图中画出平面直角坐标系,并标出主要建筑C(3,2)的位置;
(2)标志点A与主要建筑C的图上距离为 .
21.(6分)如图,AB∥CD,直线EF分别与直线AB、直线CD相交于点E,F,点G在CD上,EG平分∠BEF.若∠EGC=58°,求∠EFD的度数.
22.(8分)为提高学生对计算机的兴趣,某校举办计算机汉字输入比赛.甲、乙两组各有10名学生参赛,两组学生每分钟输入汉字的个数如表:
输入汉字(个) 132 133 134 135 136 137
甲组人数(人) 1 0 1 5 2 1
乙组人数(人) 0 1 4 1 2 2
(1)请将表中的相关数据补充完整:
组别 众数(个) 中位数(个) 平均数(个) 方差
甲组 135 135
乙组 134.5 1.8
(2)请根据所学的统计知识,从两个不同角度对甲、乙两组学生的比赛成绩进行分析.
23.(10分)小明和小亮两人各带20元钱同时到一家文具店购买同一型号的中性笔和笔记本,这种中性笔每盒10支,如果整盒买比单支买每支可优惠0.2元.小明要买3支中性笔和4本笔记本,需花费19元;小亮要买7支中性笔和3本笔记本,需花费19元.
(1)求笔记本的单价和单独购买一支中性笔的价格;
(2)小明和小亮都还想再买一件单价为1.5元的小工艺品,他们利用所带的钱,能否做到既买全了想要的文具,又都能买到一件小工艺品?请通过计算说明.
24.(10分)【课本再现】
已知:如图1,P是三角形ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明:如图2,延长BP,交AC于点 D.
∵∠BPC是△PCD的一个外角(外角的定义),
∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角).
∵∠PDC是△ABD的一个外角(外角的定义),
∴∠PDC>∠A(三角形的一个外角大于任何一个和它不相邻的内角).
∴∠BPC>∠A.
【知识迁移】
如图3,求证:
(1)∠FHG>∠E;
(2)∠FHG=∠E+∠F+∠G.
【拓展延伸】
如图4,五角星五个“角”的和为 °.
25.(12分)甲、乙两人在相邻的直跑道上进行了一次60m折返跑(即跑60m后马上折返跑回起点)训练.甲完成一次折返跑用时20s,乙完成一次折返跑用时24s.假设两人同时从同一起跑线出发,且跑步过程中保持匀速.设甲、乙两人离起点的距离为y(m),跑步时间为x(s).
(1)请在直角坐标系中分别画出在本次折返跑过程中表示两人离起点的距离y与跑步时间x之间关系的图象;
(2)分别写出甲折返后和乙折返前y与x之间的关系式;
(3)在出发多少s后,两人到起点的距离相等?
(4)当x为何值时,两人之间相距5米?(直接写出x的值即可)
2022-2023学年山东省青岛市黄岛区、胶州市八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题3分,共24分)在每个题给出的四个选项中,只有一项是符合题目要求的.
1.(3分)的绝对值是( )
A. B. C.5 D.﹣5
【分析】根据绝对值的概念得出结论即可.
【解答】解:﹣的绝对值是,
故选:A.
2.(3分)将一个直角三角形的三边长同时扩大10倍,得到的三角形是( )
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
【分析】根据勾股定理得出a2+b2=c2,推出100a2+100b2=100c2,得出(10a)2+(10b)2=(10c)2,根据勾股定理的逆定理得出即可.
【解答】解:如图,设直角三角形ABC的三边的长是a、b、c,则a2+b2=c2,
∴100a2+100b2=100c2,
即(10a)2+(10b)2=(10c)2,
∴将一个直角三角形的三边长同时扩大10倍,得到的三角形是直角三角形,
故选:C.
3.(3分)青岛火车站是一座百年老站,是青岛市的标志性建筑之一.下列能准确表示青岛火车站地理位置的是( )
A.山东省青岛市
B.青岛市市南区泰安路2号
C.栈桥风景区的西北方向
D.胶州湾隧道口大约2千米处
【分析】根据坐标确定位置的方法,结合具体的情景进行判断即可.
【解答】解:根据坐标确定位置的方法可知,
A.山东省青岛市,只是确定了一个范围,不是一个具体的点,因此选项A不符合题意;
B.青岛市市南区泰安路2号,确定了点的位置,因此选项B符合题意;
C.栈桥风景区的西北方向,具体位置不确定,无法确定青岛火车站的位置,因此选项C不符合题意;
D.胶州湾隧道口大约2千米处,只是确定一个范围,不能确定火车站的具体的位置点,因此选项D不符合题意;
故选:B.
4.(3分)要说明命题“若|a|>5,则a>5”是假命题,可以举的一个反例是( )
A.a=5 B.a=﹣5 C.a=6 D.a=﹣6
【分析】举的反例是满足条件,但不能得到结论,据此可得答案.
【解答】解:a=﹣6时,满足|a|>5,但﹣6<5,
故选:D.
5.(3分)小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
【分析】根据中位数定义可得答案.
【解答】解:中位数与计算结果与被涂污数字无关,
故选:D.
6.(3分)如图是一个“数值转换机”的示意图,当输入81时,输出的值是( )
A. B.3 C.3 D.9
【分析】理解“数值转换机”的示意图,代入求值即可.
【解答】解:根据题意有,输出的值为:.
故选:A.
7.(3分)已知直线y=3x与y=﹣2x+b的交点的坐标为(1,a),则a+b的值为( )
A.2 B.4 C.8 D.15
【分析】根据直线y=3x与y=﹣2x+b的交点的坐标为(1,a),先求出a的值,再待定系数法求出b的值,进一步求解即可.
【解答】解:∵直线y=3x与y=﹣2x+b的交点的坐标为(1,a),
∴a=3×1=3,
将点(1,3)代入y=﹣2x+b,
得﹣2+b=3,
解得b=5,
∴a+b=3+5=8,
故选:C.
8.(3分)如图,在平面直角坐标系中,A1(1,﹣2),A2(2,0),A3(3,2),A4(4,0),…根据这个规律,点A2023的坐标是( )
A.(2022,0) B.(2023,0) C.(2023,2) D.(2023,﹣2)
【分析】由图形得出点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,继而求得答案.
【解答】解:观察图形可知,
点的横坐标依次是1、2、3、4、…、n,纵坐标依次是﹣2、0、2、0、﹣2、0、2、…,四个一循环,
2023÷4=505……3,
所以点A2023坐标是(2023,2).
故选:C.
二、填空题(本大题共8小题,每小题3分,共24分)
9.(3分)写一个大于2且小于3的无理数 (答案不唯一) .
【分析】根据算术平方根的性质可以把2和3写成带根号的形式,再进一步写出一个被开方数介于两者之间的数即可.
【解答】解:∵2=,3=,
∴写出一个大于2小于3的无理数是、等.
故答案为:(答案不唯一).
10.(3分)为参加校运会,小强同学进行立定跳远训练,其中6次的成绩如下(单位:m):2.2,2.6,2.4,2.5,2.4,2.4.这6次成绩的极差是 0.4 m.
【分析】根据极差的定义求解即可.
【解答】解:这组数据的极差为2.6﹣2.2=0.4m,
故答案为:0.4.
11.(3分)某校规定:学生的平时测试、期中测试、期末测试三项成绩分别按20%,40%,40%的比例计入学期总评成绩.小明的平时测试、期中测试、期末测试的体育成绩依次为90分,90分,95分,则小明这学期的体育总评成绩为 92 分.
【分析】这学期总评成绩是平时测试、期中测试、期末测试的体育成绩与其对应百分比的乘积之和.
【解答】解:小明这学期总评成绩=90×20%+90×40%+95×40%=36+18.4+34=92(分).
故答案为:92.
12.(3分)若是二元一次方程ax+by=﹣2的一个解,则3a﹣2b+2024的值为 2022 .
【分析】把解代入二元一次方程中,把得到的等式和代数式整理变形,整体代入求值.
【解答】解:∵若是二元一次方程ax+by=﹣2的一个解,
∴3a﹣2b=﹣2,
∴3a﹣2b+2024
=﹣2+2024
=2022,
故答案为:2022.
13.(3分)现规定一种运算:a※b=ab+a﹣b,其中a,b为实数.例如:1※(﹣5)=1×(﹣5)+1﹣(﹣5)=1,则※的值为 ﹣1 .
【分析】读懂新定义,利用新定义计算.
【解答】解:※=2※(﹣3)=2×(﹣3)+2﹣(﹣3)=﹣6+2+3=﹣1,
故答案为:﹣1.
14.(3分)两个两位数的差是18,在较大的两位数的右边接着写上较小的两位数,得到一个四位数;在较大的两位数的左边写上较小的两位数,也得到一个四位数.若这两个四位数的和是6666,这两个两位数分别是多少?设较大的两位数为x,较小的两位数为y,根据题意列出的方程组为 .
【分析】首先设较大的两位数为x,较小的两位数为y,根据题意可得等量关系:①两个两位数的差是18,②100x+y与100y+x的和是6666,根据等量关系列出方程组即可.
【解答】解:设较大的两位数为x,较小的两位数为y,
根据题意,得.
故答案为:.
15.(3分)请写出一个满足条件①②的一次函数关系式y= ﹣x﹣3(答案不唯一) .
①图象不经过第一象限,且与y轴交于负半轴;
②当x=﹣3时,y=0.
【分析】设一次函数的关系式为y=kx+b(k≠0),由①,利用一次函数图象与系数的关系,可得出k<0,b<0,由②,利用一次函数图象上点的坐标特征,可求出b=3k,代入k=﹣1即可得出结论.
【解答】解:设一次函数的关系式为y=kx+b(k≠0),
∵该函数图象不经过第一象限,且与y轴交于负半轴,
∴k<0,b<0;
∵当x=﹣3时,y=0,
∴﹣3k+b=0,
∴b=3k.
当k=﹣1时,b=3k=3×(﹣1)=﹣3,
∴一次函数关系式可以为y=﹣x﹣3.
故答案为:﹣x﹣3(答案不唯一).
16.(3分)如图是某滑雪场U型池的示意图,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3的半圆,其边缘AB=CD=16,点E在CD上,CE=4.一名滑雪爱好者从A点滑到E点时,他滑行的最短路程约为 16 (π取3).
【分析】要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.
【解答】解:如图是其侧面展开图:AD=3×3=9,AB=CD=16.DE=CD﹣CE=16﹣4=12,
在Rt△ADE中,AE===16.
故他滑行的最短距离约为16.
故答案为:16.
三、作图题(本题满分4分)
17.(4分)已知:△ABC.
求作:直线AD,使得AD∥BC.
【分析】作∠DAC=∠C,则根据平行线的判定方法可判断AD∥BC.
【解答】解:如图,
四、解答题(本大题共8小题,共68分)
18.(8分)(1)计算:﹣;
(2)计算:(2+)(2﹣)﹣10.
【分析】(1)直接化简二次根式,进而计算得出答案;
(2)直接利用平方差公式化简,进而得出答案.
【解答】解:(1)原式=2﹣
=;
(2)原式=(2)2﹣()2﹣10
=12﹣2﹣10
=0.
19.(8分)(1)解方程组:;
(2)解方程组:.
【分析】(1)利用加减消元法进行求解即可;
(2)利用加减消元法进行求解即可.
【解答】解:(1),
①+②得:4m=12,
解得m=3,
把m=3代入②得:3+2n=5,
解得n=1,
故原方程组的解是:;
(2),
①×4得:4x﹣4y=4③,
②﹣③得:﹣y=﹣1,
解得y=1,
把y=1代入①得:x﹣1=1,
解得x=2,
故原方程组的解是:.
20.(6分)有一张图纸被污染,上面只有如图所示的两个标志点A(﹣2,1),B(﹣3,﹣4)可识别.
请根据以上信息解答下列问题:
(1)在图中画出平面直角坐标系,并标出主要建筑C(3,2)的位置;
(2)标志点A与主要建筑C的图上距离为 .
【分析】(1)根据点A(﹣2,1)确定x轴,y轴的位置,进而确定平面直角坐标系,再由点的坐标的定义确定点C的位置即可;
(2)根据网格构造直角三角形,利用勾股定理求出答案即可.
【解答】解:(1)画出平面直角坐标系,并标出主要建筑C(3,2)的位置如图所示:
(2)由网格构造直角三角形,由勾股定理得,
AC==,
故答案为:.
21.(6分)如图,AB∥CD,直线EF分别与直线AB、直线CD相交于点E,F,点G在CD上,EG平分∠BEF.若∠EGC=58°,求∠EFD的度数.
【分析】根据两直线平行,内错角相等求出∠BEG的度数,再根据角平分线的定义得到∠FEG,然后利用平行线的性质可得解.
【解答】解:∵AB∥CD,∠EGC=58°,
∴∠BEG=∠EGC=58°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=116°,
∵AB∥CD,
∴∠EFD=180°﹣∠BEF=180°﹣116°=64°.
22.(8分)为提高学生对计算机的兴趣,某校举办计算机汉字输入比赛.甲、乙两组各有10名学生参赛,两组学生每分钟输入汉字的个数如表:
输入汉字(个) 132 133 134 135 136 137
甲组人数(人) 1 0 1 5 2 1
乙组人数(人) 0 1 4 1 2 2
(1)请将表中的相关数据补充完整:
组别 众数(个) 中位数(个) 平均数(个) 方差
甲组 135 135 135 1.6
乙组 135 134.5 135 1.8
(2)请根据所学的统计知识,从两个不同角度对甲、乙两组学生的比赛成绩进行分析.
【分析】(1)根据众数、中位数、方差以及平均数的计算公式分别进行解答即可;
(2)从中位数看,甲组每分钟输入135字以上的人数比乙组多;从方差看,S2甲<S2乙;甲组成绩波动小,比较稳定.
【解答】解:(1)甲组的中位数是=135(个),
∵甲组的平均数是:×(132+134+135×5+136×2+137)=135(个),
∴甲的方差是:×[(132﹣135)2+(134﹣135)2+5×(135﹣135)2+2×(136﹣135)2+(137﹣135)2]=1.6,
乙组的众数为134(个),平均数为:×(133+134×4+135+136×2+137×2)=135(个),
补充完整如下:
组别 众数(个) 中位数(个) 平均数(个) 方差
甲组 135 135 135 1.6
乙组 134 134.5 135 1.8
(2)从中位数看,甲组每分钟输入135字以上的人数比乙组多,甲组成绩更好一些;
从方差看,S2甲<S2乙,甲组成绩波动小,比较稳定.
23.(10分)小明和小亮两人各带20元钱同时到一家文具店购买同一型号的中性笔和笔记本,这种中性笔每盒10支,如果整盒买比单支买每支可优惠0.2元.小明要买3支中性笔和4本笔记本,需花费19元;小亮要买7支中性笔和3本笔记本,需花费19元.
(1)求笔记本的单价和单独购买一支中性笔的价格;
(2)小明和小亮都还想再买一件单价为1.5元的小工艺品,他们利用所带的钱,能否做到既买全了想要的文具,又都能买到一件小工艺品?请通过计算说明.
【分析】(1)设单独购买一支中性笔的价格是x元,每本笔记本的单价是y元,依题意:小明要买3支中性笔和4本笔记本,需花费19元;小亮要买7支中性笔和3本笔记本,需花费19元.列出二元一次方程组,解方程组即可;
(2)若两人各自购买,则要买到想买的文具,小亮要花费19元,小明花费19元,则小明和小亮将无法再买一件小工艺品,若两人合在一起买文具,则买文具所需费用为36元,然后由40﹣36=4(元),1.5×2=3(元),即可得出结论.
【解答】解:(1)设单独购买一支中性笔的价格是x元,笔记本的单价是y元,
依题意得:,
解得:,
答:单独购买一支中性笔的价格是1元,笔记本的单价是4元.
(2)若两人各自购买,则要买到想买的文具,小亮要花费19元,小明花费19元,
∵小明和小亮每人有19元,
∴小明和小亮将无法再买一件小工艺品,
若两人合在一起买文具,则买文具所需费用为:(1﹣0.2)×(3+7)+4×(4+3)=36(元),
∵两人共有20+20=40(元),40﹣26=4(元),1.5×2=3(元),4﹣3=1(元),
∴两人应该合在一起买文具,才能既买到要买的文具又都能买到一件小工艺品.
24.(10分)【课本再现】
已知:如图1,P是三角形ABC内一点,连接PB,PC.
求证:∠BPC>∠A.
证明:如图2,延长BP,交AC于点 D.
∵∠BPC是△PCD的一个外角(外角的定义),
∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角).
∵∠PDC是△ABD的一个外角(外角的定义),
∴∠PDC>∠A(三角形的一个外角大于任何一个和它不相邻的内角).
∴∠BPC>∠A.
【知识迁移】
如图3,求证:
(1)∠FHG>∠E;
(2)∠FHG=∠E+∠F+∠G.
【拓展延伸】
如图4,五角星五个“角”的和为 180 °.
【分析】(1)根据三角形的外角性质进行求解即可;
(2)利用三角形的外角性质进行解答即可;
【拓展延伸】利用三角形的外角性质即可求解.
【解答】(1)证明:延长GH交EF于点A,如图3,
∵∠FAH是△AEG的外角,
∴∠FAH>∠E,
∵∠FHG是△AFH的外角,
∴∠FHG>∠FAH,
∴∠FHG>∠E;
(2)证明∵∠FAH是△AEG的外角,
∴∠FAH=∠E+∠G,
∵∠FHG是△AFH的外角,
∴∠FHG=∠FAH+∠F,
∴∠FHG=∠E+∠F+∠G;
【拓展延伸】解:如图4,
∵∠FEG是△ABE的外角,∠FGE是△CDG的外角,
∴∠EFG=∠A+∠B,∠FGE=∠C+∠D,
∵∠F+∠EFG+∠FGE=180°,
∴∠F+∠A+∠B+∠C+∠D=180°.
故答案为:180.
25.(12分)甲、乙两人在相邻的直跑道上进行了一次60m折返跑(即跑60m后马上折返跑回起点)训练.甲完成一次折返跑用时20s,乙完成一次折返跑用时24s.假设两人同时从同一起跑线出发,且跑步过程中保持匀速.设甲、乙两人离起点的距离为y(m),跑步时间为x(s).
(1)请在直角坐标系中分别画出在本次折返跑过程中表示两人离起点的距离y与跑步时间x之间关系的图象;
(2)分别写出甲折返后和乙折返前y与x之间的关系式;
(3)在出发多少s后,两人到起点的距离相等?
(4)当x为何值时,两人之间相距5米?(直接写出x的值即可)
【分析】(1)根据题意画图即可;
(2)根据(1)中的图象求出其解析式即可;
(3)根据图象,求出直线交点的横坐标即可;
(4)分类讨论,分别求出x的值即可.
【解答】解:(1)如图所示:
(2)根据题意有,
甲折返后:在10<x≤20,甲的图象是直线函数,经过点(10,60)、(20,0),
设函数解析式为y=kx+b,将点(10,60)、(20,0)代入得,
,解得:,解析式为y=﹣6x+120,
∴甲折返后y与x之间的关系式为:y=﹣6x+120,(10<x≤20;
乙折返前:在0≤x<12,乙的图象是正比例函数,经过点(12,60),
设函数解析式为y=kx,将点(12,60)代入得,60=12k,解得:k=5,解析式为y=5x;
∴乙折返前y与x之间的关系式为:y=5x,(0≤x<12);
(3)当120﹣6x=5x时,解得:x=,
∴在出发s后,两人到起点的距离相等;
(4)①当6x﹣5x=5时,解得:x=5;
②120﹣6x﹣5x=5时,解得:x=;
③5x﹣(120﹣6x)=5时,解得:x=;
④当120﹣5x﹣(120﹣6x)=5时,解得:x=5,(不符合题意,舍去);
综上所述,当x=5或x=或x=时,两人之间相距5米.
同课章节目录
