6.1.1 菱形的性质同步练习(含答案)
文档属性
| 名称 | 6.1.1 菱形的性质同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第1课时 菱形的性质
基础闯关
知识点一:菱形的定义与对称性
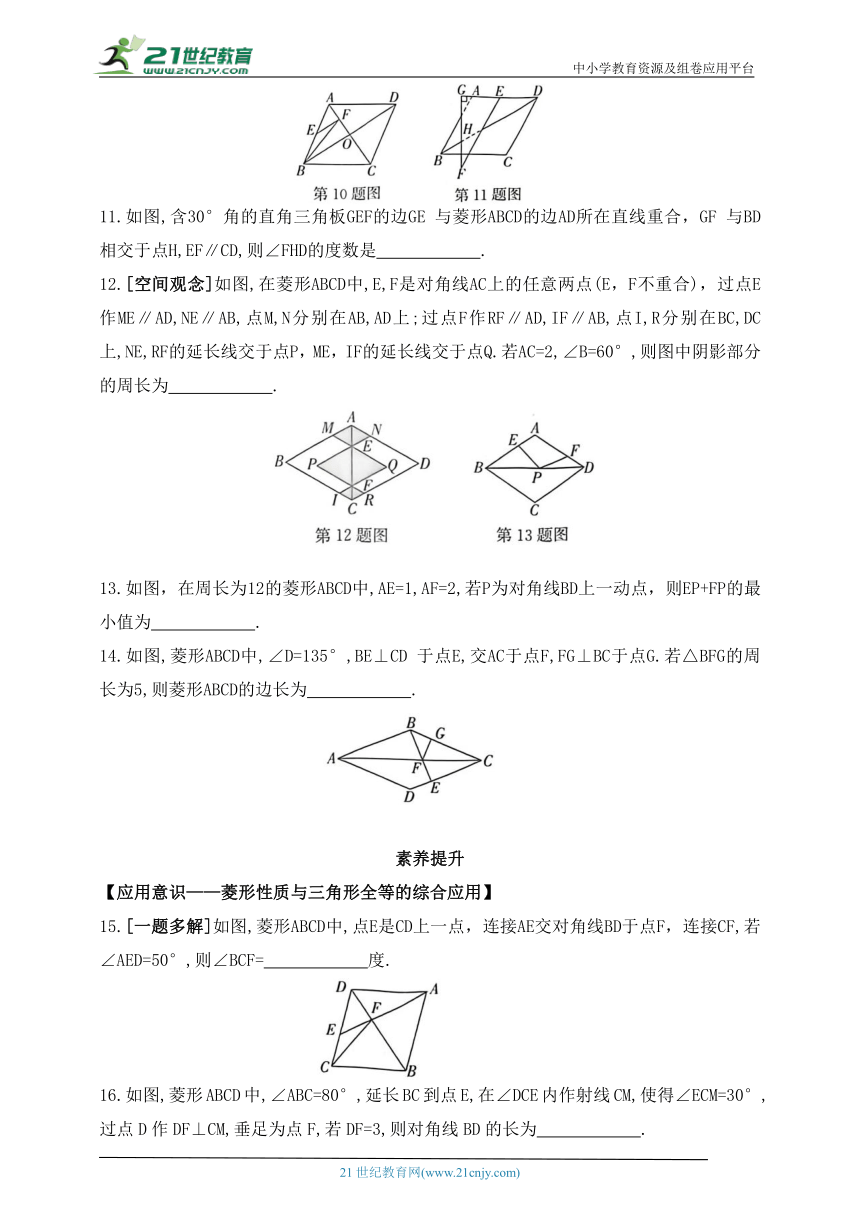
1.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
2.菱形不具备的性质是( )
A.是轴对称图形 B.对称轴有两条
C.对称轴是两条对角线 D.是中心对称图形
3.如图,菱形ABCD的顶点A,B,C的坐标分别(0,2),(2,1),(4,2),则顶点D的坐标是( )
A.( 2,2) B.( 2,4) C.( 3,2) D.( 2,3)
知识点二:菱形的性质
4.在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG的长度为( )
B.3
5.如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状变化的过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
6.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 .
能力提升
7.[空间观念]如图,在边长为的菱形ABCD 中,∠BAD=60°,点E,F分别为折线AB-BC,AD-DC上的点(不含菱形顶点),AE=AF,BF,DE相交于点G,作射线AG.甲、乙二人分别对这个问题进行了研究:
甲:射线AG不一定经过点C;
乙:当DE垂直于菱形的边时,线段AG的长可能为3.
下列判断正确的为( )
A.甲、乙都对 B.甲、乙都错 C.甲对,乙错 D.甲错,乙对
8.如图,在菱形ABCD中,点E在对角线BD 上,AE=BE,∠C=120°,若BD=12cm,则DE=__________cm.
9.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF= .
10.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,BF.若AF=1,AE=2,则FB的长为 .
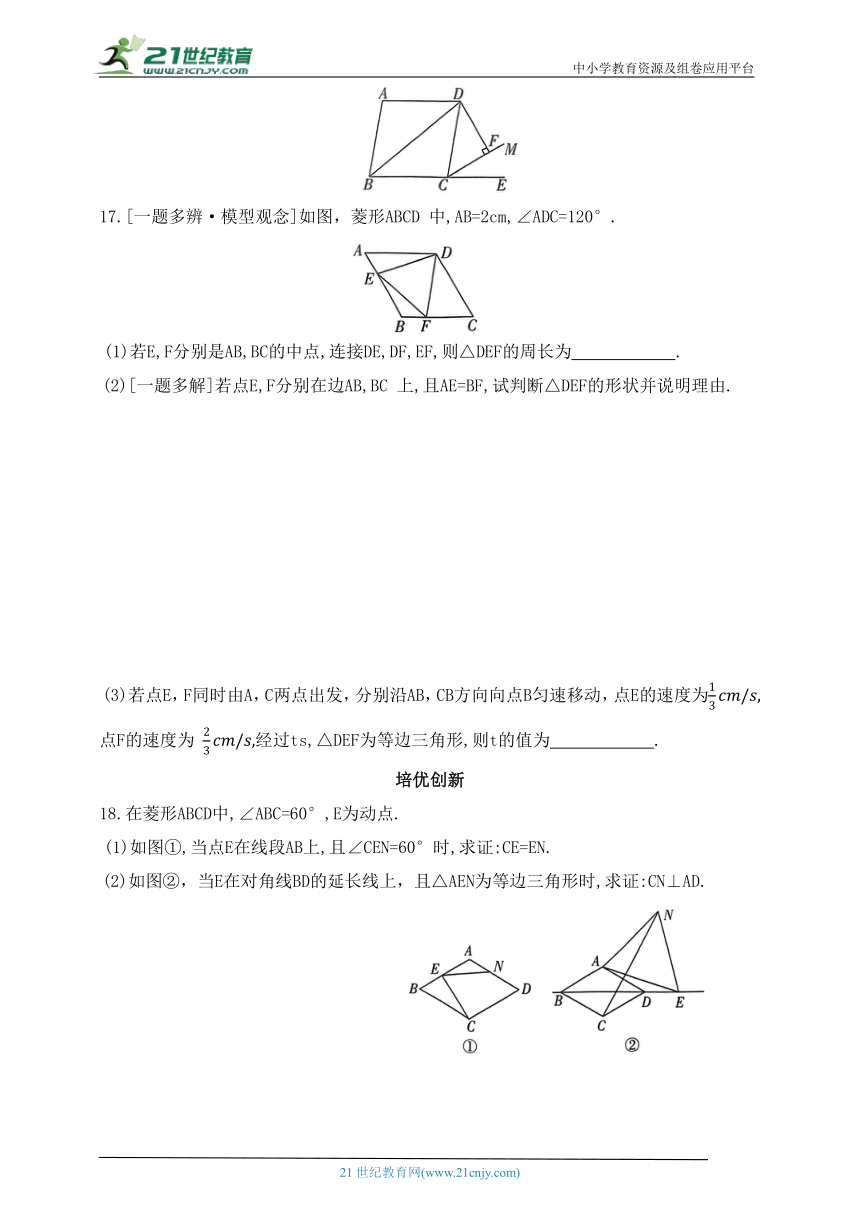
11.如图,含30°角的直角三角板GEF的边GE 与菱形ABCD的边AD所在直线重合,GF 与BD相交于点H,EF∥CD,则∠FHD的度数是 .
12.[空间观念]如图,在菱形ABCD中,E,F是对角线AC上的任意两点(E,F不重合),过点E作ME∥AD,NE∥AB,点M,N分别在AB,AD上;过点F作RF∥AD,IF∥AB,点I,R分别在BC,DC上,NE,RF的延长线交于点P,ME,IF的延长线交于点Q.若AC=2,∠B=60°,则图中阴影部分的周长为 .
13.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 .
14.如图,菱形ABCD中,∠D=135°,BE⊥CD 于点E,交AC于点F,FG⊥BC于点G.若△BFG的周长为5,则菱形ABCD的边长为 .
素养提升
【应用意识——菱形性质与三角形全等的综合应用】
15.[一题多解]如图,菱形ABCD中,点E是CD上一点,连接AE交对角线BD于点F,连接CF,若∠AED=50°,则∠BCF= 度.
16.如图,菱形ABCD中,∠ABC=80°,延长BC到点E,在∠DCE内作射线CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为点F,若DF=3,则对角线BD的长为 .
17.[一题多辨·模型观念]如图,菱形ABCD 中,AB=2cm,∠ADC=120°.
(1)若E,F分别是AB,BC的中点,连接DE,DF,EF,则△DEF的周长为 .
(2)[一题多解]若点E,F分别在边AB,BC 上,且AE=BF,试判断△DEF的形状并说明理由.
(3)若点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动,点E的速度为点F的速度为 经过ts,△DEF为等边三角形,则t的值为 .
培优创新
18.在菱形ABCD中,∠ABC=60°,E为动点.
(1)如图①,当点E在线段AB上,且∠CEN=60°时,求证:CE=EN.
(2)如图②,当E在对角线BD的延长线上,且△AEN为等边三角形时,求证:CN⊥AD.
参考答案
1.D 2.C 3.D 4.A 5.C 6.36° 7.B 8.8 9.60° 11.120° 12.8
13.3 [解析]作点F关于BD的对称点 连接交BD于点P,则 由两点之间线段最短可知,当E,P, 在一条直线上时,EP+FP的值最小,此时 ∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,
四边形 是平行四边形, 的最小值为3.
14.5
15.50 [解析]方法1:∵四边形ABCD是菱形,∴AD=CD,AD∥BC,∠ADF=∠CDF.
在△ADF和△CDF中, =∠DCF.
∵∠AED=50°,∴∠DAE+∠ADE=180°-50°=130° ,∴∠ADE+∠DCF=130°.∵AD∥BC,∴∠ADE+∠BCD=180°,∴∠ADE+∠BCF+∠DCF =180°,∴∠BCF=180°-130°=50°.方法2:∵四边形ABCD是菱形,∴BC=AB,∠CBF=∠ABF,AB∥CD,∴∠BAE=∠AED=50°.
在△CBF和△ABF中, =∠BAF=50°.
16.6 [解析]如图,连接AC交BD于点H.由菱形的性质,得∠ADC=∠ABC=80°,∠DCE=80°,∠DHC=90°.又∵∠ECM=30°,∴∠DCF=50°.∵DF⊥CM,∴∠CFD =90°,∴∠CDF=40°.又∵四边形ABCD是菱形,∴BD 平分∠ADC,∴∠HDC=40°,∴易证△CDH≌△CDF,∴DH=DF=3,∴BD=2DH=6.
(2)解:△DEF是等边三角形,理由:方法1:如图,连接DB.
∵四边形ABCD是菱形,∠ADC=120°,∴AB=BC=CD=DA,∠A=∠DBC=∠ADB=60°,
∴△ADB,△DBC为等边三角形,∴AD=BD.
在△ADE和△BDF 中, △BDF,
∴DE=DF,∠ADE=∠BDF,∴∠BDF+∠EDB=∠ADE+∠EDB=∠ADB=60°,
∴△DEF是等边三角形.
方法2:如图,延长AB至点M,使BM=AE,连接FM,则△BMF是等边三角形,可证△EMF≌△DAE,则DE=EF,∠MEF=∠ADE,∴∠MEF+∠AED=∠ADE+∠AED=120°,∴∠DEF=60°,∴△DEF是等边三角形.
(3)2
18.证明:(1)如图①,在BC上截取BF=BE,连接FE.∵BF =BE,∠B=60°,∴△BFE是等边三角形,∴∠B=∠BFE=∠BEF=60°,∴∠EFC=120°.∵四边形ABCD 是菱形,∠B=60°,∴AB=BC,∠A=120°=∠EFC,∴AE=FC.∵∠CEN=∠B=60°,∠AEC=∠B+∠BCE=∠CEN+∠AEN,∴∠BCE=∠AEN.在△AEN和△FCE中 .△AEN ≌△FCE(ASA),∴CE=EN.
(2)如图②,连接AC,设AD与CN的交点为O.∵四边形ABCD是菱形,∠ABC =60°,∴AB=BC,∠ABD=30°,∴△ABC是等边三角形,∴AB=AC,∠BAC=60°.∵△AEN是等边三角形,∴AN=AE,∠NAE=60° =∠BAC,∴∠BAE=∠CAN.
在△ABE和△ACN中, ∴△ABE≌△ACN(SAS),∴∠ABE=∠ACN=30°.
∵∠BAC=∠CAD=60°,∴∠AOC=90°,∴CN⊥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第1课时 菱形的性质
基础闯关
知识点一:菱形的定义与对称性
1.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是( )
A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC
2.菱形不具备的性质是( )
A.是轴对称图形 B.对称轴有两条
C.对称轴是两条对角线 D.是中心对称图形
3.如图,菱形ABCD的顶点A,B,C的坐标分别(0,2),(2,1),(4,2),则顶点D的坐标是( )
A.( 2,2) B.( 2,4) C.( 3,2) D.( 2,3)
知识点二:菱形的性质
4.在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG的长度为( )
B.3
5.如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状变化的过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
6.如图,五边形ABCDE是正五边形,以AB为边,在五边形ABCDE的内部作菱形ABCF,则∠FAE的度数为 .
能力提升
7.[空间观念]如图,在边长为的菱形ABCD 中,∠BAD=60°,点E,F分别为折线AB-BC,AD-DC上的点(不含菱形顶点),AE=AF,BF,DE相交于点G,作射线AG.甲、乙二人分别对这个问题进行了研究:
甲:射线AG不一定经过点C;
乙:当DE垂直于菱形的边时,线段AG的长可能为3.
下列判断正确的为( )
A.甲、乙都对 B.甲、乙都错 C.甲对,乙错 D.甲错,乙对
8.如图,在菱形ABCD中,点E在对角线BD 上,AE=BE,∠C=120°,若BD=12cm,则DE=__________cm.
9.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF= .
10.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AB,AO的中点,连接EF,BF.若AF=1,AE=2,则FB的长为 .
11.如图,含30°角的直角三角板GEF的边GE 与菱形ABCD的边AD所在直线重合,GF 与BD相交于点H,EF∥CD,则∠FHD的度数是 .
12.[空间观念]如图,在菱形ABCD中,E,F是对角线AC上的任意两点(E,F不重合),过点E作ME∥AD,NE∥AB,点M,N分别在AB,AD上;过点F作RF∥AD,IF∥AB,点I,R分别在BC,DC上,NE,RF的延长线交于点P,ME,IF的延长线交于点Q.若AC=2,∠B=60°,则图中阴影部分的周长为 .
13.如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为 .
14.如图,菱形ABCD中,∠D=135°,BE⊥CD 于点E,交AC于点F,FG⊥BC于点G.若△BFG的周长为5,则菱形ABCD的边长为 .
素养提升
【应用意识——菱形性质与三角形全等的综合应用】
15.[一题多解]如图,菱形ABCD中,点E是CD上一点,连接AE交对角线BD于点F,连接CF,若∠AED=50°,则∠BCF= 度.
16.如图,菱形ABCD中,∠ABC=80°,延长BC到点E,在∠DCE内作射线CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为点F,若DF=3,则对角线BD的长为 .
17.[一题多辨·模型观念]如图,菱形ABCD 中,AB=2cm,∠ADC=120°.
(1)若E,F分别是AB,BC的中点,连接DE,DF,EF,则△DEF的周长为 .
(2)[一题多解]若点E,F分别在边AB,BC 上,且AE=BF,试判断△DEF的形状并说明理由.
(3)若点E,F同时由A,C两点出发,分别沿AB,CB方向向点B匀速移动,点E的速度为点F的速度为 经过ts,△DEF为等边三角形,则t的值为 .
培优创新
18.在菱形ABCD中,∠ABC=60°,E为动点.
(1)如图①,当点E在线段AB上,且∠CEN=60°时,求证:CE=EN.
(2)如图②,当E在对角线BD的延长线上,且△AEN为等边三角形时,求证:CN⊥AD.
参考答案
1.D 2.C 3.D 4.A 5.C 6.36° 7.B 8.8 9.60° 11.120° 12.8
13.3 [解析]作点F关于BD的对称点 连接交BD于点P,则 由两点之间线段最短可知,当E,P, 在一条直线上时,EP+FP的值最小,此时 ∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,
四边形 是平行四边形, 的最小值为3.
14.5
15.50 [解析]方法1:∵四边形ABCD是菱形,∴AD=CD,AD∥BC,∠ADF=∠CDF.
在△ADF和△CDF中, =∠DCF.
∵∠AED=50°,∴∠DAE+∠ADE=180°-50°=130° ,∴∠ADE+∠DCF=130°.∵AD∥BC,∴∠ADE+∠BCD=180°,∴∠ADE+∠BCF+∠DCF =180°,∴∠BCF=180°-130°=50°.方法2:∵四边形ABCD是菱形,∴BC=AB,∠CBF=∠ABF,AB∥CD,∴∠BAE=∠AED=50°.
在△CBF和△ABF中, =∠BAF=50°.
16.6 [解析]如图,连接AC交BD于点H.由菱形的性质,得∠ADC=∠ABC=80°,∠DCE=80°,∠DHC=90°.又∵∠ECM=30°,∴∠DCF=50°.∵DF⊥CM,∴∠CFD =90°,∴∠CDF=40°.又∵四边形ABCD是菱形,∴BD 平分∠ADC,∴∠HDC=40°,∴易证△CDH≌△CDF,∴DH=DF=3,∴BD=2DH=6.
(2)解:△DEF是等边三角形,理由:方法1:如图,连接DB.
∵四边形ABCD是菱形,∠ADC=120°,∴AB=BC=CD=DA,∠A=∠DBC=∠ADB=60°,
∴△ADB,△DBC为等边三角形,∴AD=BD.
在△ADE和△BDF 中, △BDF,
∴DE=DF,∠ADE=∠BDF,∴∠BDF+∠EDB=∠ADE+∠EDB=∠ADB=60°,
∴△DEF是等边三角形.
方法2:如图,延长AB至点M,使BM=AE,连接FM,则△BMF是等边三角形,可证△EMF≌△DAE,则DE=EF,∠MEF=∠ADE,∴∠MEF+∠AED=∠ADE+∠AED=120°,∴∠DEF=60°,∴△DEF是等边三角形.
(3)2
18.证明:(1)如图①,在BC上截取BF=BE,连接FE.∵BF =BE,∠B=60°,∴△BFE是等边三角形,∴∠B=∠BFE=∠BEF=60°,∴∠EFC=120°.∵四边形ABCD 是菱形,∠B=60°,∴AB=BC,∠A=120°=∠EFC,∴AE=FC.∵∠CEN=∠B=60°,∠AEC=∠B+∠BCE=∠CEN+∠AEN,∴∠BCE=∠AEN.在△AEN和△FCE中 .△AEN ≌△FCE(ASA),∴CE=EN.
(2)如图②,连接AC,设AD与CN的交点为O.∵四边形ABCD是菱形,∠ABC =60°,∴AB=BC,∠ABD=30°,∴△ABC是等边三角形,∴AB=AC,∠BAC=60°.∵△AEN是等边三角形,∴AN=AE,∠NAE=60° =∠BAC,∴∠BAE=∠CAN.
在△ABE和△ACN中, ∴△ABE≌△ACN(SAS),∴∠ABE=∠ACN=30°.
∵∠BAC=∠CAD=60°,∴∠AOC=90°,∴CN⊥AD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
