6.1.2 菱形的判定同步练习(含答案)
文档属性
| 名称 | 6.1.2 菱形的判定同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
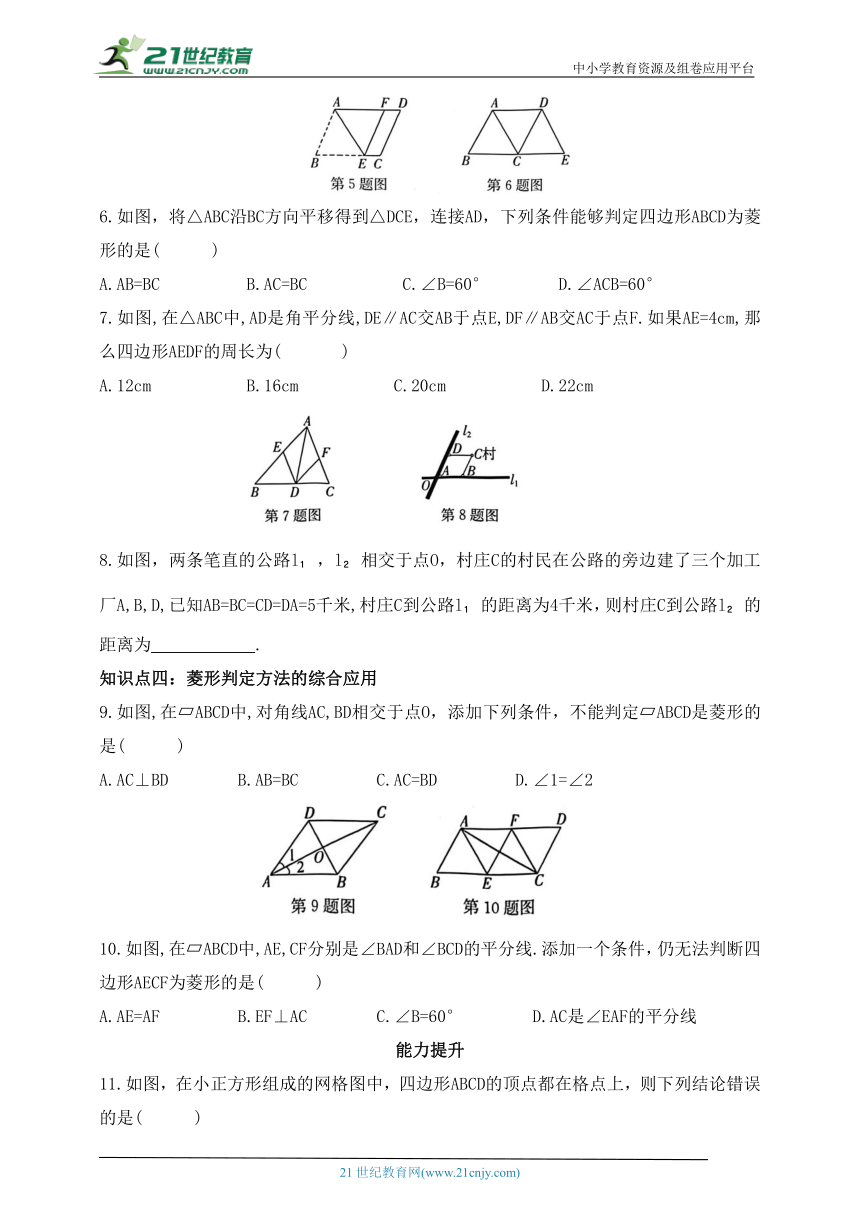
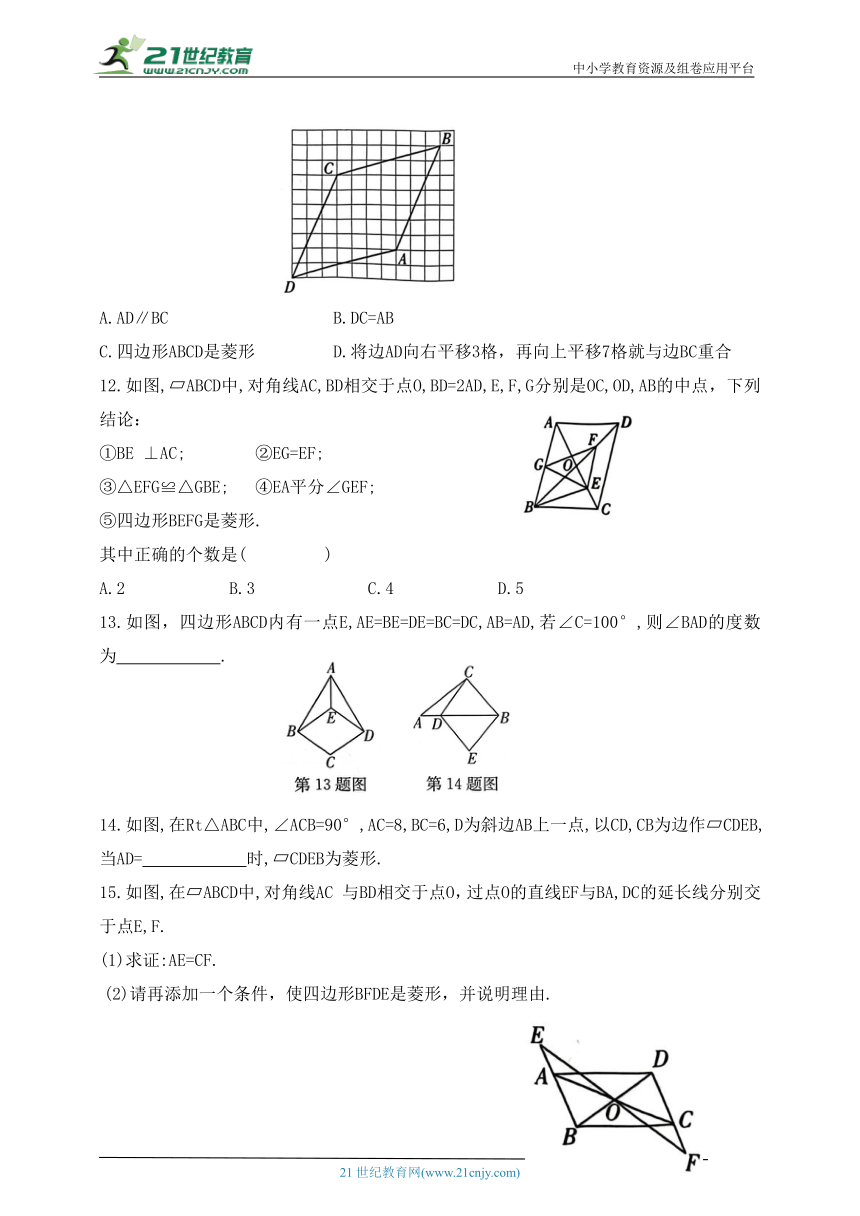
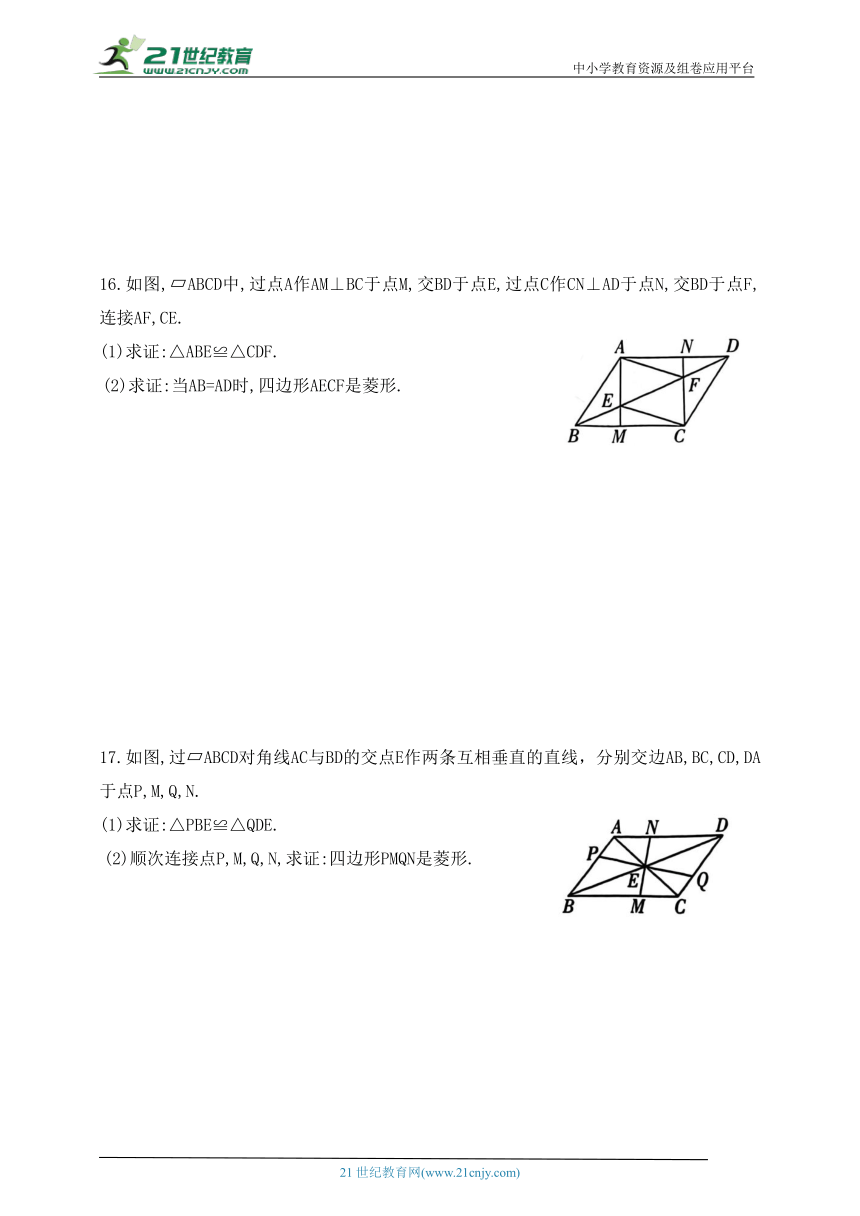
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第2课时 菱形的判定
基础闯关
知识点一:利用定义判定菱形
1.如图,四边形ABCD是平行四边形,延长BA 到点E,使AE=AB,连接ED,EC,AC.添加一个条件,能使四边形ACDE成为菱形的是( )
A.AB=AD B.AB=ED C.CD=AE D.EC=AD
2.如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,要使四边形AFDE为菱形,△ABC应满足的条件是 .(添加一个条件即可)
知识点二:利用对角线的位置关系判定菱形
3.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
4.从下图入口处进入,最后到达的是( )
A.甲 B.乙 C.丙 D.丁
知识点三:利用边的关系判定菱形
5.如图,将平行四边形ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF B.AB=EF C.AE=AF D.AF=BE
6.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
7.如图,在△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.如果AE=4cm,那么四边形AEDF的周长为( )
A.12cm B.16cm C.20cm D.22cm
8.如图,两条笔直的公路l ,l 相交于点O,村庄C的村民在公路的旁边建了三个加工厂A,B,D,已知AB=BC=CD=DA=5千米,村庄C到公路l 的距离为4千米,则村庄C到公路l 的距离为 .
知识点四:菱形判定方法的综合应用
9.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件,不能判定 ABCD是菱形的是( )
A.AC⊥BD B.AB=BC C.AC=BD D.∠1=∠2
10.如图,在 ABCD中,AE,CF分别是∠BAD和∠BCD的平分线.添加一个条件,仍无法判断四边形AECF为菱形的是( )
A.AE=AF B.EF⊥AC C.∠B=60° D.AC是∠EAF的平分线
能力提升
11.如图,在小正方形组成的网格图中,四边形ABCD的顶点都在格点上,则下列结论错误的是( )
A.AD∥BC B.DC=AB
C.四边形ABCD是菱形 D.将边AD向右平移3格,再向上平移7格就与边BC重合
12.如图, ABCD中,对角线AC,BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:
①BE ⊥AC; ②EG=EF;
③△EFG≌△GBE; ④EA平分∠GEF;
⑤四边形BEFG是菱形.
其中正确的个数是( )
A.2 B.3 C.4 D.5
13.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠BAD的度数为 .
14.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD,CB为边作 CDEB,当AD= 时, CDEB为菱形.
15.如图,在 ABCD中,对角线AC 与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:AE=CF.
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
16.如图, ABCD中,过点A作AM⊥BC于点M,交BD于点E,过点C作CN⊥AD于点N,交BD于点F,连接AF,CE.
(1)求证:△ABE≌△CDF.
(2)求证:当AB=AD时,四边形AECF是菱形.
17.如图,过 ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB,BC,CD,DA于点P,M,Q,N.
(1)求证:△PBE≌△QDE.
(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.
培优创新
【求解中点四边形的关键——中位线】
18.如图,在四边形ABCD 中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.四边形ABCD是梯形
B.四边形ABCD是菱形
C.对角线AC=BD
D.AD=BC
19.如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P,Q,M,N分别为AB,BC,CD,DA的中点,求证:四边形MNPQ是菱形.
参考答案
1.B 2.示例:AB=AC 3.C 4.D 5.C 6.A 7.B 8.4千米 9.C 10.C 11.C 12.C 13.50° 14.2.8
15.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,BE∥DF,∴∠E=∠F.
在△AOE和△COF中, CF.
(2)解:示例:当EF⊥BD时,四边形BFDE是菱形.理由:如图,连接BF,DE.∵四边形ABCD是平行四边形,∴OB=OD.∵△AOE≌△COF,∴OE=OF,∴四边形BFDE是平行四边形.∵EF⊥BD,∴四边形BFDE 是菱形.
16.证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∠ABM=∠CDN,
∴∠ABE=∠CDF.
∵AM⊥BC,CN⊥AD,∴∠AMB=∠CND=90°,∴∠BAM=∠DCN,
在△ABE和△CDF中, ∴△ABE≌△CDF(ASA).
(2)如图,连接AC.当AB=AD时,四边形ABCD为菱形,则AC⊥BD,AD∥BC.∵△ABE≌△CDF,∴AE=CF.∵AM⊥BC,CN⊥AD,AD∥BC,∴AM∥CN,∴四边形AECF为平行四边形.∵AC⊥EF,∴四边形AECF为菱形.
17.证明:(1)∵四边形ABCD是平行四边形,∴EB=ED,AB∥CD,∴∠EBP=∠EDQ.
在△PBE和△QDE中,
(2)如图所示,∵△PBE≌△QDE,∴EP=EQ.同理,△BME≌△DNE(ASA),∴EM=EN,∴四边形PMQN 是平行四边形.∵PQ⊥MN,∴四边形PMQN是菱形.
18.D
19.证明:如图,连接BD,AC.∵△ADE和△BCE都是等边三角形,∴AE=DE,EC=BE,∠AED=∠BEC=60°,∴∠AEC=∠DEB=120°,∴△AEC≌△DEB(SAS),∴AC=BD.∵M,N是CD,DA的中点,∴MN是△ACD的中位线,即 同理可得NP= QM,∴四边形MNPQ是菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第2课时 菱形的判定
基础闯关
知识点一:利用定义判定菱形
1.如图,四边形ABCD是平行四边形,延长BA 到点E,使AE=AB,连接ED,EC,AC.添加一个条件,能使四边形ACDE成为菱形的是( )
A.AB=AD B.AB=ED C.CD=AE D.EC=AD
2.如图,在△ABC中,点D,E,F分别是边BC,CA,AB的中点,要使四边形AFDE为菱形,△ABC应满足的条件是 .(添加一个条件即可)
知识点二:利用对角线的位置关系判定菱形
3.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,DE=DF.在下列条件中,使四边形BECF是菱形的是( )
A.EB⊥EC B.AB⊥AC C.AB=AC D.BF∥CE
4.从下图入口处进入,最后到达的是( )
A.甲 B.乙 C.丙 D.丁
知识点三:利用边的关系判定菱形
5.如图,将平行四边形ABCD沿AE翻折,使点B恰好落在AD上的点F处,则下列结论不一定成立的是( )
A.AF=EF B.AB=EF C.AE=AF D.AF=BE
6.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ABCD为菱形的是( )
A.AB=BC B.AC=BC C.∠B=60° D.∠ACB=60°
7.如图,在△ABC中,AD是角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F.如果AE=4cm,那么四边形AEDF的周长为( )
A.12cm B.16cm C.20cm D.22cm
8.如图,两条笔直的公路l ,l 相交于点O,村庄C的村民在公路的旁边建了三个加工厂A,B,D,已知AB=BC=CD=DA=5千米,村庄C到公路l 的距离为4千米,则村庄C到公路l 的距离为 .
知识点四:菱形判定方法的综合应用
9.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件,不能判定 ABCD是菱形的是( )
A.AC⊥BD B.AB=BC C.AC=BD D.∠1=∠2
10.如图,在 ABCD中,AE,CF分别是∠BAD和∠BCD的平分线.添加一个条件,仍无法判断四边形AECF为菱形的是( )
A.AE=AF B.EF⊥AC C.∠B=60° D.AC是∠EAF的平分线
能力提升
11.如图,在小正方形组成的网格图中,四边形ABCD的顶点都在格点上,则下列结论错误的是( )
A.AD∥BC B.DC=AB
C.四边形ABCD是菱形 D.将边AD向右平移3格,再向上平移7格就与边BC重合
12.如图, ABCD中,对角线AC,BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点,下列结论:
①BE ⊥AC; ②EG=EF;
③△EFG≌△GBE; ④EA平分∠GEF;
⑤四边形BEFG是菱形.
其中正确的个数是( )
A.2 B.3 C.4 D.5
13.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠BAD的度数为 .
14.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,D为斜边AB上一点,以CD,CB为边作 CDEB,当AD= 时, CDEB为菱形.
15.如图,在 ABCD中,对角线AC 与BD相交于点O,过点O的直线EF与BA,DC的延长线分别交于点E,F.
(1)求证:AE=CF.
(2)请再添加一个条件,使四边形BFDE是菱形,并说明理由.
16.如图, ABCD中,过点A作AM⊥BC于点M,交BD于点E,过点C作CN⊥AD于点N,交BD于点F,连接AF,CE.
(1)求证:△ABE≌△CDF.
(2)求证:当AB=AD时,四边形AECF是菱形.
17.如图,过 ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB,BC,CD,DA于点P,M,Q,N.
(1)求证:△PBE≌△QDE.
(2)顺次连接点P,M,Q,N,求证:四边形PMQN是菱形.
培优创新
【求解中点四边形的关键——中位线】
18.如图,在四边形ABCD 中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
A.四边形ABCD是梯形
B.四边形ABCD是菱形
C.对角线AC=BD
D.AD=BC
19.如图,在四边形ABCD中,E是AB上的一点,△ADE和△BCE都是等边三角形,点P,Q,M,N分别为AB,BC,CD,DA的中点,求证:四边形MNPQ是菱形.
参考答案
1.B 2.示例:AB=AC 3.C 4.D 5.C 6.A 7.B 8.4千米 9.C 10.C 11.C 12.C 13.50° 14.2.8
15.(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,BE∥DF,∴∠E=∠F.
在△AOE和△COF中, CF.
(2)解:示例:当EF⊥BD时,四边形BFDE是菱形.理由:如图,连接BF,DE.∵四边形ABCD是平行四边形,∴OB=OD.∵△AOE≌△COF,∴OE=OF,∴四边形BFDE是平行四边形.∵EF⊥BD,∴四边形BFDE 是菱形.
16.证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∠ABM=∠CDN,
∴∠ABE=∠CDF.
∵AM⊥BC,CN⊥AD,∴∠AMB=∠CND=90°,∴∠BAM=∠DCN,
在△ABE和△CDF中, ∴△ABE≌△CDF(ASA).
(2)如图,连接AC.当AB=AD时,四边形ABCD为菱形,则AC⊥BD,AD∥BC.∵△ABE≌△CDF,∴AE=CF.∵AM⊥BC,CN⊥AD,AD∥BC,∴AM∥CN,∴四边形AECF为平行四边形.∵AC⊥EF,∴四边形AECF为菱形.
17.证明:(1)∵四边形ABCD是平行四边形,∴EB=ED,AB∥CD,∴∠EBP=∠EDQ.
在△PBE和△QDE中,
(2)如图所示,∵△PBE≌△QDE,∴EP=EQ.同理,△BME≌△DNE(ASA),∴EM=EN,∴四边形PMQN 是平行四边形.∵PQ⊥MN,∴四边形PMQN是菱形.
18.D
19.证明:如图,连接BD,AC.∵△ADE和△BCE都是等边三角形,∴AE=DE,EC=BE,∠AED=∠BEC=60°,∴∠AEC=∠DEB=120°,∴△AEC≌△DEB(SAS),∴AC=BD.∵M,N是CD,DA的中点,∴MN是△ACD的中位线,即 同理可得NP= QM,∴四边形MNPQ是菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
