6.1.3 菱形的性质与判定的综合应用同步练习(含答案)
文档属性
| 名称 | 6.1.3 菱形的性质与判定的综合应用同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第3课时 菱形的性质与判定的综合应用
基础闯关
知识点一:利用对角线计算菱形的面积
1.若菱形两条对角线的长分别是6cm和8cm,则其面积为 cm .
2.已知一个菱形的边长为2,较长的对角线长为,则这个菱形的面积是 .
3.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH=_______________.
4.如图,在∠MON的两边上分别截取OA,OB,使OA=OB,分别以点A,B为圆心,OA长为半径作弧,两弧交于点C,连接AC,BC,AB,OC.若AB=2cm,四边形OACB的面积为4cm ,则OC的长为__________cm.
知识点二:菱形性质与判定的综合应用
5.如图,两张等宽的纸条交叉重叠在一起,重叠部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D 之间的距离为8cm ,则线段AB的长为( )
A.5cm B.4.8cm C.4.6 cm D.4cm
6.如图,AC,BD是菱形ABCD的对角线,E,F 分别是边AB,AD的中点,连接EF,EO,FO,则下列结论错误的是( )
A.EF=DO B.EF⊥AO C.四边形EOFA是菱形 D.四边形EBOF是菱形
7.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为 .
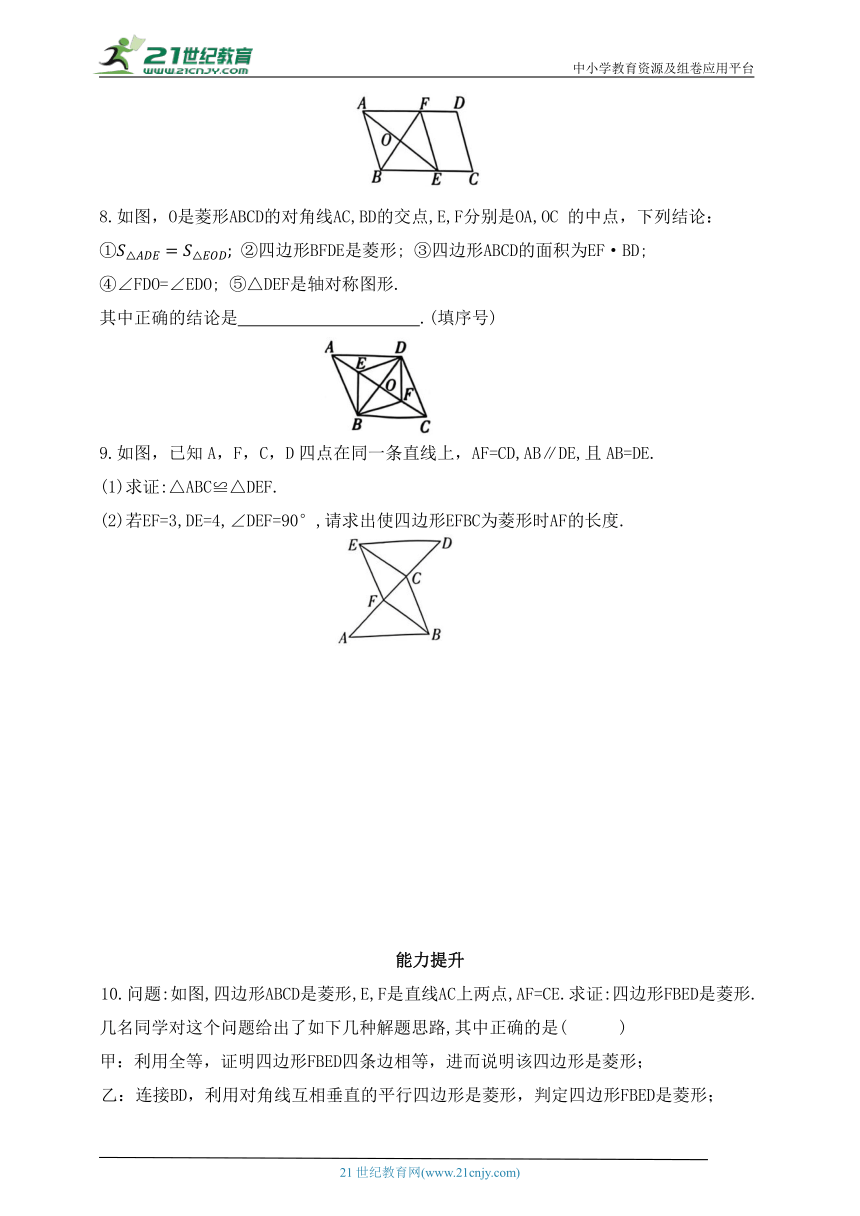
8.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC 的中点,下列结论:
① ②四边形BFDE是菱形; ③四边形ABCD的面积为EF·BD;
④∠FDO=∠EDO; ⑤△DEF是轴对称图形.
其中正确的结论是 .(填序号)
9.如图,已知A,F,C,D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF.
(2)若EF=3,DE=4,∠DEF=90°,请求出使四边形EFBC为菱形时AF的长度.
能力提升
10.问题:如图,四边形ABCD是菱形,E,F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
几名同学对这个问题给出了如下几种解题思路,其中正确的是( )
甲:利用全等,证明四边形FBED四条边相等,进而说明该四边形是菱形;
乙:连接BD,利用对角线互相垂直的平行四边形是菱形,判定四边形FBED是菱形;
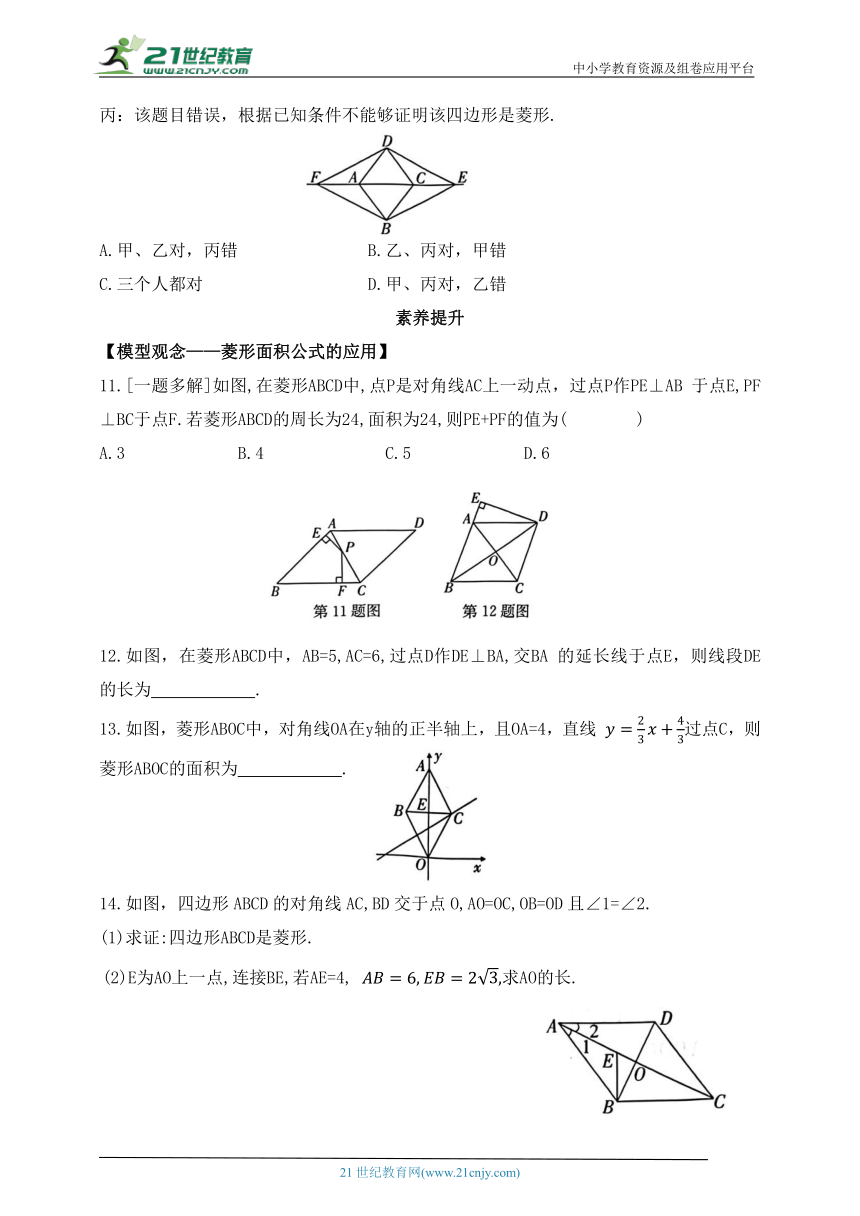
丙:该题目错误,根据已知条件不能够证明该四边形是菱形.
A.甲、乙对,丙错 B.乙、丙对,甲错
C.三个人都对 D.甲、丙对,乙错
素养提升
【模型观念——菱形面积公式的应用】
11.[一题多解]如图,在菱形ABCD中,点P是对角线AC上一动点,过点P作PE⊥AB 于点E,PF⊥BC于点F.若菱形ABCD的周长为24,面积为24,则PE+PF的值为( )
A.3 B.4 C.5 D.6
12.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA 的延长线于点E,则线段DE的长为 .
13.如图,菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线 过点C,则菱形ABOC的面积为 .
14.如图,四边形ABCD的对角线AC,BD交于点O,AO=OC,OB=OD且∠1=∠2.
(1)求证:四边形ABCD是菱形.
(2)E为AO上一点,连接BE,若AE=4, 求AO的长.
15.如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂足为点E,点F在AD的延长线上,CF⊥AD,垂足为点F.
(1)若∠BAD=60°,求证:四边形CEHF是菱形.
(2)若CE=8,△ACE的面积为64,求菱形ABCD的面积.
培优创新
16.已知:BD是△ABC的角平分线,点E在AB边上,BE=BC,过点E作EF∥AC,交BD于点F,连接CF,DE.
(1)如图①,求证:四边形CDEF是菱形.
(2)如图②,当∠DEF=90°,AC=BC时,在不添加任何辅助线的情况下,请直接写出图
②中度数为∠ABD度数2倍的角.
参考答案
1.24 4.4 5.A 6.D
7.16 8.①②③④⑤
9.(1)证明:∵AB∥DE,∴∠A=∠D.∵AF=CD,∴AF+FC=CD+FC,即AC=DF.∵AB=DE,∴△ABC≌△DEF(SAS).(2)解:如图,连接EB交AD于点O.在Rt△EFD中,∵∠DEF=90°,EF=3,DE=4,∴DF=5.∵四边形EFBC是菱形,
10.A
11.B [解析]方法1:如图,延长FP交AD于点G,易证GP =EP.∵菱形ABCD的周长为24,∴BC=6.∵菱形ABCD的面积为24,∴FG=24÷6=4,∴PE+PF=GF =4.方法2:如图,连接BP,则 =12,∴AB·PE+BC·PF=24,即6(PE+PF)=24,∴PE+PF=4.
[解析]∵四边形ABCD是菱形,AC=6,∴AC⊥
·
13.4
14.(1)证明:∵AO=OC,OB=OD,∴四边形ABCD是平行四边形,∴AD∥BC,∴∠2=∠ACB.∵∠1=∠2,∴∠1=∠ACB,∴AB=CB,∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,∴AC⊥BD.在Rt△ABO和Rt△EBO中,根据勾股定理得 OB =AB -AO =BE -OE . 设OE=x.∵AE=4,AB=6,EB= 解得x=1,∴AO=AE+OE=4+1=5.
15.(1)证明:∵CE⊥AB,CF⊥AD,∴∠AEC=∠AFC=90°.
∵四边形ABCD是菱形,∴∠CAE=∠CAF=
∵点H为对角线AC的中点,易证=FH=CF,
∴四边形CEHF是菱形.
(2)解:∵四边形ABCD是菱形,∴AB=CB.∵CE⊥AB,△ACE的面积为64,
即 16.
设AB=CB=x,则BE=16-x.在Rt△BCE中,由勾股定理,得8 +(16-x) =x ,解得x=10,
∴AB=10
16.(1)证明:在△BDE和△BDC中, ∴△BDE≌△BDC(SAS),
∴DE=DC,∠BDE=∠BDC.同理,△BFE≌△BFC,∴EF=CF.
∵EF∥AC,∴∠EFD=∠BDC,∴∠EFD=∠BDE,∴DE=EF,
∴DE=EF=CF=DC,∴四边形CDEF是菱形.
(2)度数为∠ABD度数2倍的角是∠A,∠ABC,∠FEB,∠FCB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第3课时 菱形的性质与判定的综合应用
基础闯关
知识点一:利用对角线计算菱形的面积
1.若菱形两条对角线的长分别是6cm和8cm,则其面积为 cm .
2.已知一个菱形的边长为2,较长的对角线长为,则这个菱形的面积是 .
3.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AH⊥BC于点H,已知BO=4,S菱形ABCD=24,则AH=_______________.
4.如图,在∠MON的两边上分别截取OA,OB,使OA=OB,分别以点A,B为圆心,OA长为半径作弧,两弧交于点C,连接AC,BC,AB,OC.若AB=2cm,四边形OACB的面积为4cm ,则OC的长为__________cm.
知识点二:菱形性质与判定的综合应用
5.如图,两张等宽的纸条交叉重叠在一起,重叠部分为四边形ABCD,若测得点A,C之间的距离为6cm,点B,D 之间的距离为8cm ,则线段AB的长为( )
A.5cm B.4.8cm C.4.6 cm D.4cm
6.如图,AC,BD是菱形ABCD的对角线,E,F 分别是边AB,AD的中点,连接EF,EO,FO,则下列结论错误的是( )
A.EF=DO B.EF⊥AO C.四边形EOFA是菱形 D.四边形EBOF是菱形
7.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为 .
8.如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC 的中点,下列结论:
① ②四边形BFDE是菱形; ③四边形ABCD的面积为EF·BD;
④∠FDO=∠EDO; ⑤△DEF是轴对称图形.
其中正确的结论是 .(填序号)
9.如图,已知A,F,C,D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF.
(2)若EF=3,DE=4,∠DEF=90°,请求出使四边形EFBC为菱形时AF的长度.
能力提升
10.问题:如图,四边形ABCD是菱形,E,F是直线AC上两点,AF=CE.求证:四边形FBED是菱形.
几名同学对这个问题给出了如下几种解题思路,其中正确的是( )
甲:利用全等,证明四边形FBED四条边相等,进而说明该四边形是菱形;
乙:连接BD,利用对角线互相垂直的平行四边形是菱形,判定四边形FBED是菱形;
丙:该题目错误,根据已知条件不能够证明该四边形是菱形.
A.甲、乙对,丙错 B.乙、丙对,甲错
C.三个人都对 D.甲、丙对,乙错
素养提升
【模型观念——菱形面积公式的应用】
11.[一题多解]如图,在菱形ABCD中,点P是对角线AC上一动点,过点P作PE⊥AB 于点E,PF⊥BC于点F.若菱形ABCD的周长为24,面积为24,则PE+PF的值为( )
A.3 B.4 C.5 D.6
12.如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA 的延长线于点E,则线段DE的长为 .
13.如图,菱形ABOC中,对角线OA在y轴的正半轴上,且OA=4,直线 过点C,则菱形ABOC的面积为 .
14.如图,四边形ABCD的对角线AC,BD交于点O,AO=OC,OB=OD且∠1=∠2.
(1)求证:四边形ABCD是菱形.
(2)E为AO上一点,连接BE,若AE=4, 求AO的长.
15.如图,四边形ABCD是菱形,点H为对角线AC的中点,点E在AB的延长线上,CE⊥AB,垂足为点E,点F在AD的延长线上,CF⊥AD,垂足为点F.
(1)若∠BAD=60°,求证:四边形CEHF是菱形.
(2)若CE=8,△ACE的面积为64,求菱形ABCD的面积.
培优创新
16.已知:BD是△ABC的角平分线,点E在AB边上,BE=BC,过点E作EF∥AC,交BD于点F,连接CF,DE.
(1)如图①,求证:四边形CDEF是菱形.
(2)如图②,当∠DEF=90°,AC=BC时,在不添加任何辅助线的情况下,请直接写出图
②中度数为∠ABD度数2倍的角.
参考答案
1.24 4.4 5.A 6.D
7.16 8.①②③④⑤
9.(1)证明:∵AB∥DE,∴∠A=∠D.∵AF=CD,∴AF+FC=CD+FC,即AC=DF.∵AB=DE,∴△ABC≌△DEF(SAS).(2)解:如图,连接EB交AD于点O.在Rt△EFD中,∵∠DEF=90°,EF=3,DE=4,∴DF=5.∵四边形EFBC是菱形,
10.A
11.B [解析]方法1:如图,延长FP交AD于点G,易证GP =EP.∵菱形ABCD的周长为24,∴BC=6.∵菱形ABCD的面积为24,∴FG=24÷6=4,∴PE+PF=GF =4.方法2:如图,连接BP,则 =12,∴AB·PE+BC·PF=24,即6(PE+PF)=24,∴PE+PF=4.
[解析]∵四边形ABCD是菱形,AC=6,∴AC⊥
·
13.4
14.(1)证明:∵AO=OC,OB=OD,∴四边形ABCD是平行四边形,∴AD∥BC,∴∠2=∠ACB.∵∠1=∠2,∴∠1=∠ACB,∴AB=CB,∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,∴AC⊥BD.在Rt△ABO和Rt△EBO中,根据勾股定理得 OB =AB -AO =BE -OE . 设OE=x.∵AE=4,AB=6,EB= 解得x=1,∴AO=AE+OE=4+1=5.
15.(1)证明:∵CE⊥AB,CF⊥AD,∴∠AEC=∠AFC=90°.
∵四边形ABCD是菱形,∴∠CAE=∠CAF=
∵点H为对角线AC的中点,易证=FH=CF,
∴四边形CEHF是菱形.
(2)解:∵四边形ABCD是菱形,∴AB=CB.∵CE⊥AB,△ACE的面积为64,
即 16.
设AB=CB=x,则BE=16-x.在Rt△BCE中,由勾股定理,得8 +(16-x) =x ,解得x=10,
∴AB=10
16.(1)证明:在△BDE和△BDC中, ∴△BDE≌△BDC(SAS),
∴DE=DC,∠BDE=∠BDC.同理,△BFE≌△BFC,∴EF=CF.
∵EF∥AC,∴∠EFD=∠BDC,∴∠EFD=∠BDE,∴DE=EF,
∴DE=EF=CF=DC,∴四边形CDEF是菱形.
(2)度数为∠ABD度数2倍的角是∠A,∠ABC,∠FEB,∠FCB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
