6.2矩形的性质与判定 第1课时 矩形的性质 同步练习(含答案)
文档属性
| 名称 | 6.2矩形的性质与判定 第1课时 矩形的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 12:23:49 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
2 矩形的性质与判定
第1课时 矩形的性质
基础闯关
知识点一:矩形的定义
1.下列说法不正确的是( )
A.矩形是平行四边形 B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形 D.平行四边形具有的性质矩形都有
2.在平行四边形ABCD中,AB=3,BC=4,当□ABCD的面积最大时,下列结论正确的有( )
①AC=5; ②∠A+∠C=180°; ③AC⊥BD; ④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
知识点二:矩形边、角的性质
3.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
4.如图所示,把矩形纸片ABCD沿EF折叠后,点D,C分别落在 的位置.若∠EFB=65°,则 等于( )
A.70° B.65° C.50° D.25°
知识点三:矩形对角线的性质
5.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分
C.对角线相等 D.对角线互相垂直
6.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
A.4 B.8 C.10 D.12
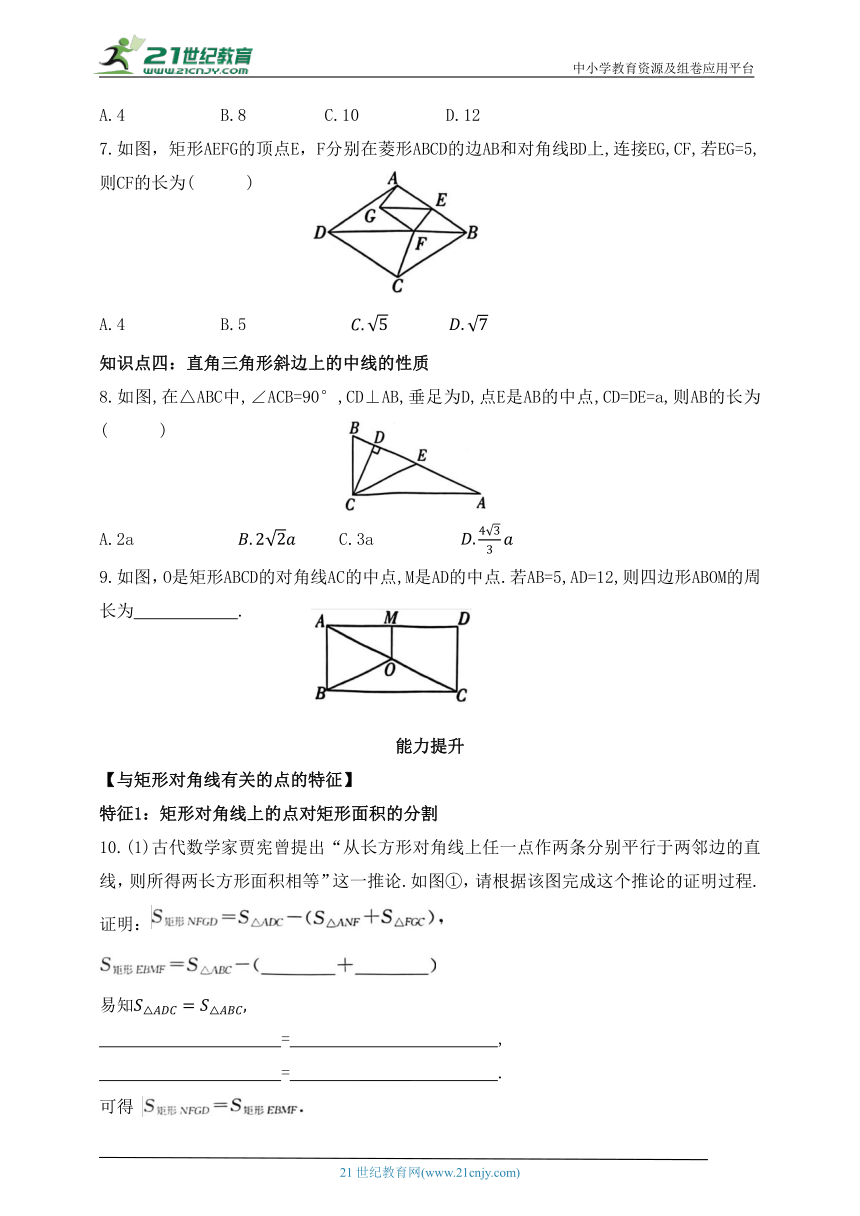
7.如图,矩形AEFG的顶点E,F分别在菱形ABCD的边AB和对角线BD上,连接EG,CF,若EG=5,则CF的长为( )
A.4 B.5
知识点四:直角三角形斜边上的中线的性质
8.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
A.2a C.3a
9.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
能力提升
【与矩形对角线有关的点的特征】
特征1:矩形对角线上的点对矩形面积的分割
10.(1)古代数学家贾宪曾提出“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等”这一推论.如图①,请根据该图完成这个推论的证明过程.
证明:
易知
= ,
= ______ .
可得
(2)如图②,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8,则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
特征2:两条对角线对矩形面积的分割
11.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
特征3:过对角线交点的直线对矩形的分割
12.如图,矩形ABCD 中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC 的长为( )
C.10 D.8
13.如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF.
(1)求证:△ABE≌△CDF.
(2)当AC⊥EF时,四边形AECF是菱形吗 请说明理由.
培优创新
14.)如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=2,求菱形ABCD 的周长.
参考答案
1.B 2.B 3.C 4.C 5.C 6.B 7.B 8.B 9.20
(2)C
11.A [解析]如图,连接OP,作PE⊥AC于点E,PF⊥BD
于点F.∵矩形的两条边AB,BC的长分别为6和8,
12.A [解析]如图,连接AE,设AC与EF交于点O.∵EF是AC的垂直平分线,∴OA=OC,AE=CE.∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠OAF=∠OCE.
在△AOF和△COE中, ∴△AOF≌△COE(ASA),
∴AF=CE=5,∴AE=CE=
13.(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,AD∥BC.
在Rt△ABE和Rt△CDF 中,
(2)解:当AC⊥EF时,四边形AECF是菱形.理由如下:
∵△ABE≌△CDF,∴BE=DF.∵BC=AD,∴CE=AF.
∵CE∥AF,∴四边形AECF是平行四边形.
又∵AC⊥EF,∴四边形AECF是菱形.
14.(1)证明:∵四边形EFGH是矩形,∴EH=FG,EH∥FG,∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,∴∠BFG=∠DHE.
∵四边形ABCD是菱形,∴AD∥BC,∴∠GBF=∠EDH,∴△BGF≌△DEH(AAS),∴BG=DE.
(2)解:如图,连接EG.∵四边形ABCD是菱形,∴AD=BC,AD∥BC.
∵E为AD中点,∴AE=ED.∵BG=DE,∴AE=BG.
∵AE∥BG,∴四边形ABGE是平行四边形,∴AB=EG.
∵四边形EFGH是矩形,∴EG=FH=2,∴AB=2,
∴菱形ABCD的周长=2×4=8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
2 矩形的性质与判定
第1课时 矩形的性质
基础闯关
知识点一:矩形的定义
1.下列说法不正确的是( )
A.矩形是平行四边形 B.矩形不一定是平行四边形
C.有一个角是直角的平行四边形是矩形 D.平行四边形具有的性质矩形都有
2.在平行四边形ABCD中,AB=3,BC=4,当□ABCD的面积最大时,下列结论正确的有( )
①AC=5; ②∠A+∠C=180°; ③AC⊥BD; ④AC=BD.
A.①②③ B.①②④ C.②③④ D.①③④
知识点二:矩形边、角的性质
3.如图,矩形ABCD的顶点A,C分别在直线a,b上,且a∥b,∠1=60°,则∠2的度数为( )
A.30° B.45° C.60° D.75°
4.如图所示,把矩形纸片ABCD沿EF折叠后,点D,C分别落在 的位置.若∠EFB=65°,则 等于( )
A.70° B.65° C.50° D.25°
知识点三:矩形对角线的性质
5.下列结论中,矩形具有而菱形不一定具有的性质是( )
A.内角和为360° B.对角线互相平分
C.对角线相等 D.对角线互相垂直
6.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为( )
A.4 B.8 C.10 D.12
7.如图,矩形AEFG的顶点E,F分别在菱形ABCD的边AB和对角线BD上,连接EG,CF,若EG=5,则CF的长为( )
A.4 B.5
知识点四:直角三角形斜边上的中线的性质
8.如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
A.2a C.3a
9.如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若AB=5,AD=12,则四边形ABOM的周长为 .
能力提升
【与矩形对角线有关的点的特征】
特征1:矩形对角线上的点对矩形面积的分割
10.(1)古代数学家贾宪曾提出“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等”这一推论.如图①,请根据该图完成这个推论的证明过程.
证明:
易知
= ,
= ______ .
可得
(2)如图②,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8,则图中阴影部分的面积为( )
A.10 B.12 C.16 D.18
特征2:两条对角线对矩形面积的分割
11.如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线AC和BD的距离之和是( )
A.4.8 B.5 C.6 D.7.2
特征3:过对角线交点的直线对矩形的分割
12.如图,矩形ABCD 中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC 的长为( )
C.10 D.8
13.如图,在矩形ABCD中,E,F分别是BC,AD边上的点,且AE=CF.
(1)求证:△ABE≌△CDF.
(2)当AC⊥EF时,四边形AECF是菱形吗 请说明理由.
培优创新
14.)如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)求证:BG=DE.
(2)若E为AD中点,FH=2,求菱形ABCD 的周长.
参考答案
1.B 2.B 3.C 4.C 5.C 6.B 7.B 8.B 9.20
(2)C
11.A [解析]如图,连接OP,作PE⊥AC于点E,PF⊥BD
于点F.∵矩形的两条边AB,BC的长分别为6和8,
12.A [解析]如图,连接AE,设AC与EF交于点O.∵EF是AC的垂直平分线,∴OA=OC,AE=CE.∵四边形ABCD是矩形,∴∠B=90°,AD∥BC,∴∠OAF=∠OCE.
在△AOF和△COE中, ∴△AOF≌△COE(ASA),
∴AF=CE=5,∴AE=CE=
13.(1)证明:∵四边形ABCD是矩形,∴∠B=∠D=90°,AB=CD,AD=BC,AD∥BC.
在Rt△ABE和Rt△CDF 中,
(2)解:当AC⊥EF时,四边形AECF是菱形.理由如下:
∵△ABE≌△CDF,∴BE=DF.∵BC=AD,∴CE=AF.
∵CE∥AF,∴四边形AECF是平行四边形.
又∵AC⊥EF,∴四边形AECF是菱形.
14.(1)证明:∵四边形EFGH是矩形,∴EH=FG,EH∥FG,∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,∴∠BFG=∠DHE.
∵四边形ABCD是菱形,∴AD∥BC,∴∠GBF=∠EDH,∴△BGF≌△DEH(AAS),∴BG=DE.
(2)解:如图,连接EG.∵四边形ABCD是菱形,∴AD=BC,AD∥BC.
∵E为AD中点,∴AE=ED.∵BG=DE,∴AE=BG.
∵AE∥BG,∴四边形ABGE是平行四边形,∴AB=EG.
∵四边形EFGH是矩形,∴EG=FH=2,∴AB=2,
∴菱形ABCD的周长=2×4=8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
