6.2矩形的性质与判定 第2课时 矩形的判定 同步练习(含答案)
文档属性
| 名称 | 6.2矩形的性质与判定 第2课时 矩形的判定 同步练习(含答案) | 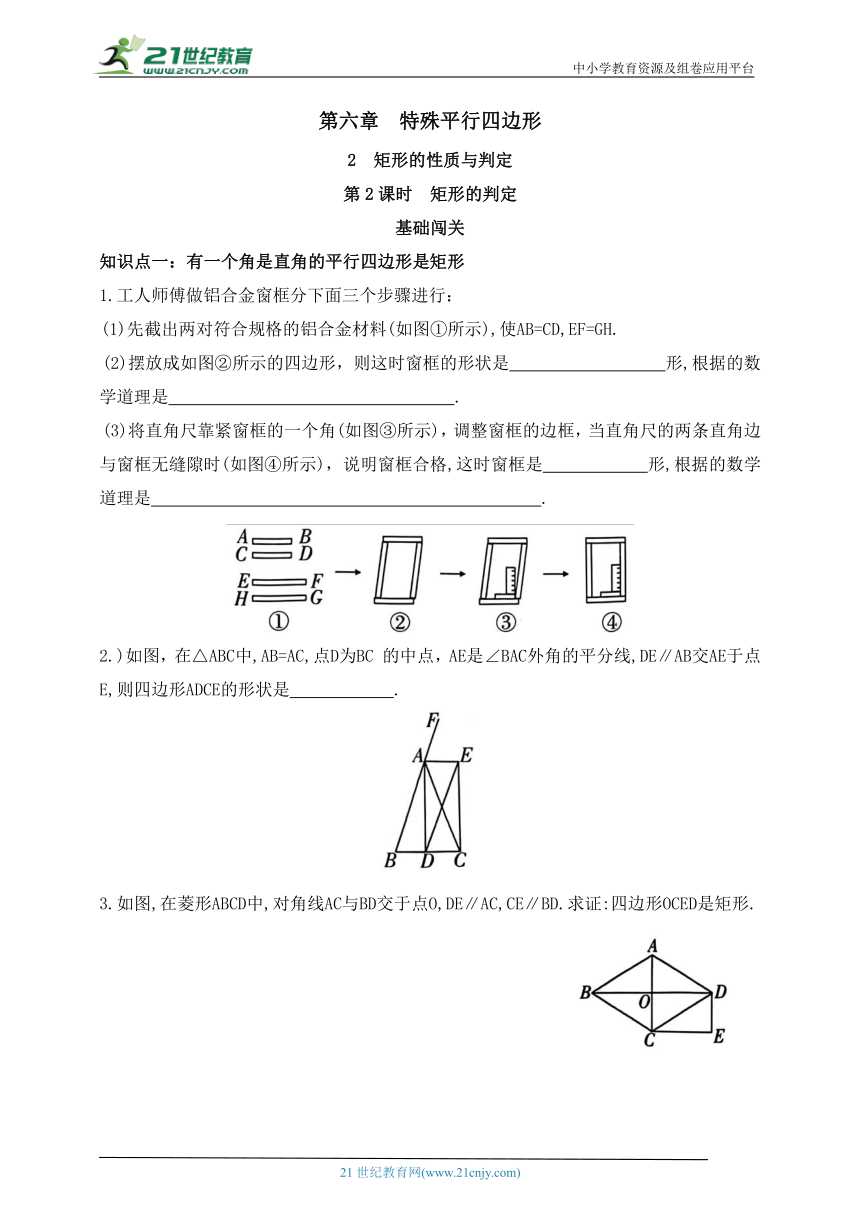 | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 12:16:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
2 矩形的性质与判定
第2课时 矩形的判定
基础闯关
知识点一:有一个角是直角的平行四边形是矩形
1.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金材料(如图①所示),使AB=CD,EF=GH.
(2)摆放成如图②所示的四边形,则这时窗框的形状是 形,根据的数学道理是 .
(3)将直角尺靠紧窗框的一个角(如图③所示),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④所示),说明窗框合格,这时窗框是 形,根据的数学道理是 .
2.)如图,在△ABC中,AB=AC,点D为BC 的中点,AE是∠BAC外角的平分线,DE∥AB交AE于点E,则四边形ADCE的形状是 .
3.如图,在菱形ABCD中,对角线AC与BD交于点O,DE∥AC,CE∥BD.求证:四边形OCED是矩形.
知识点二:对角线相等的平行四边形是矩形
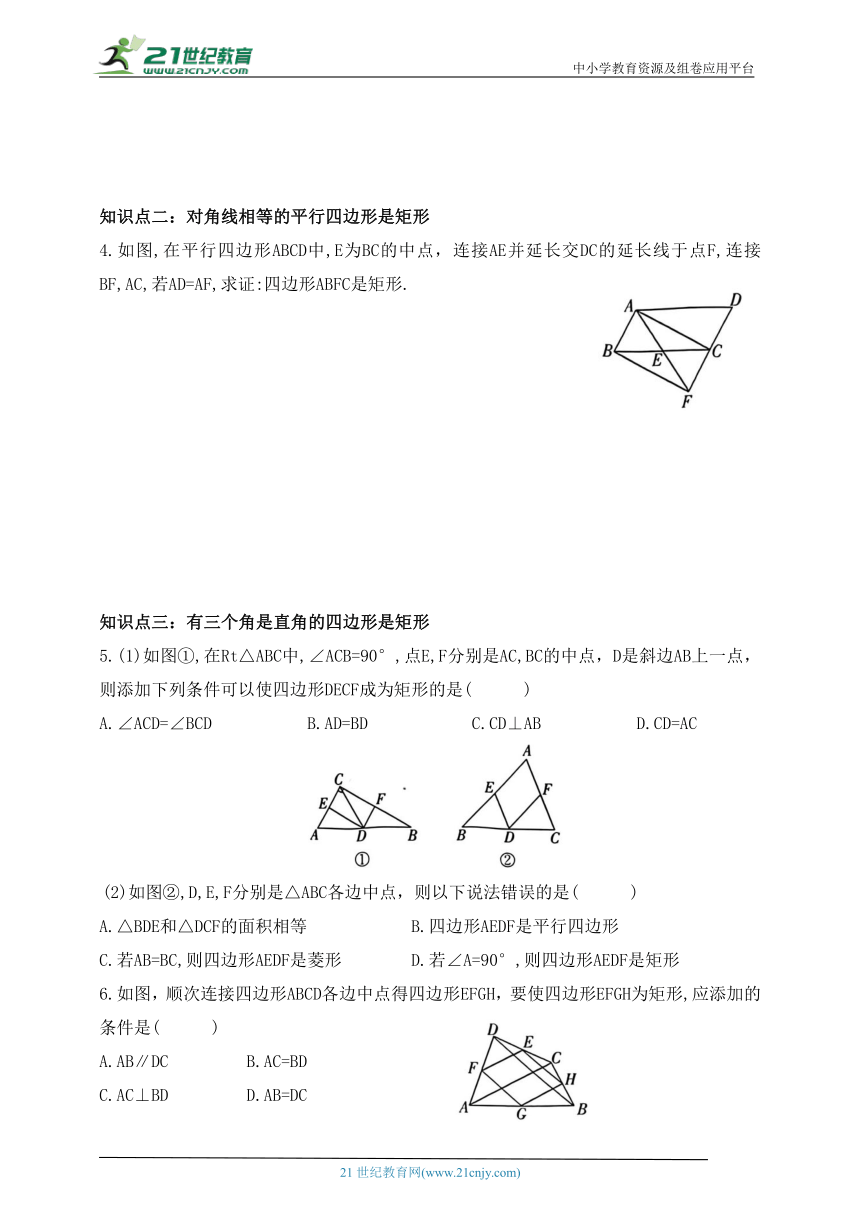
4.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
知识点三:有三个角是直角的四边形是矩形
5.(1)如图①,在Rt△ABC中,∠ACB=90°,点E,F分别是AC,BC的中点,D是斜边AB上一点,则添加下列条件可以使四边形DECF成为矩形的是( )
A.∠ACD=∠BCD B.AD=BD C.CD⊥AB D.CD=AC
(2)如图②,D,E,F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等 B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形 D.若∠A=90°,则四边形AEDF是矩形
6.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.AB=DC
能力提升
7.如图,在△ABC中,分别取AB,AC的中点D,E,连接DE,过点A作AF⊥DE,垂足为点F,将△ADF,△AEF分别绕点D,E旋转180°,拼接成四边形BCHG,连接BH.若DE=4,AF=6,则BH的长度为 .
8.如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且FG=5cm,EF=3cm,则菱形ABCD的面积是 cm .
9.如图,AB∥CD,点E,F分别在AB,CD上,连接EF.∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.求证:四边形EGFH是矩形.
10.如图①,在 ABCD中,连接对角线BD,过点A,C分别作AE⊥BD,CF⊥BD,垂足为点E,F.
(1)求证:AE=CF.
(2)如图②,延长AE至点G,使得AE=GE,连接CG,求证:四边形EGCF是矩形.
培优创新
11.如图,在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰△ADE,且∠ADE=∠ABC,连接CE,过点E作EF∥BC交CA的延长线于点F,连接BF.
(1)求证:∠ECA=∠ABC.
(2)如果AF=AB,求证:四边形FBDE是矩形.
参考答案
1.(2)平行四边 两组对边分别相等的四边形是平行四边形(3)矩 有一个角是直角的平行四边形是矩形
2.矩形
3.证明:∵CE∥BD,DE∥AC,∴四边形OCED是平行四边形.
∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°,∴四边形OCED是矩形.
4.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC,∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.
∵AB∥CF,∴四边形ABFC是平行四边形.
∵AD=BC,AD=AF,∴BC=AF,∴四边形ABFC是矩形.
5.( 1)B ( 2)C 6.C 7.10
8.24 如图,连接AC,BD,交点为O,EF与AC交于点M,EG与BD交于点N.
∵四边形ABCD是菱形,∴AC⊥BD.
∵E,F,G分别是AD,AB,CD的中点,∴EF∥∥
∴四边形OMEN是矩形,∴∠FEG=90°.
∵FG=5cm,EF=3cm,∴EG=∴
∴菱形ABCD的面积 24(cm ).
9.证明:∵EH平分
平分
∥ ∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH =
∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°.
同理可得∠EGF=90°.
∵EG平分
∵EH平分
∵点A,E,B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,
90°,即∠GEH=90°,
∴四边形EGFH是矩形.
10.证明:(1)∵四边形ABCD为平行四边形,∴AB∥CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD = 90°.
在△ABE和△CDF中, CF.
(2)由(1)得AE=CF.∵AE=GE,∴GE=CF.
∵AE⊥BD,CF⊥BD,∴AE∥CF,即EG∥CF,∴四边形EGCF是平行四边形.
∵AE⊥DB,∴∠DEG=90°,∴四边形EGCF是矩形.
11.证明:(1)∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°-2∠ABC.
同理,∠DAE=180°-2∠ADE.
∵∠ABC=∠ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,∴△ABD≌△ACE (SAS),∴∠ECA=∠ABC.
(2)∵∠ECA=∠ABC,∠ABC=∠ACB,∴∠ECF=∠ACB.
∵EF∥BC,∴∠EFC=∠ACB,∴∠EFC=∠ECF,∴EF=EC.
∵△ABD≌△ACE,∴BD=EC,∴BD=EF,∴四边形FBDE是平行四边形.
∵AF=AB=AC,∴∠AFB=∠ABF,∠ABC=∠ACB.
∵∠AFB+∠ABF+∠ABC +∠ACB=180°,∴∠ABF+∠ABC=90°,即∠CBF=90°,
∴四边形FBDE是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
2 矩形的性质与判定
第2课时 矩形的判定
基础闯关
知识点一:有一个角是直角的平行四边形是矩形
1.工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金材料(如图①所示),使AB=CD,EF=GH.
(2)摆放成如图②所示的四边形,则这时窗框的形状是 形,根据的数学道理是 .
(3)将直角尺靠紧窗框的一个角(如图③所示),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④所示),说明窗框合格,这时窗框是 形,根据的数学道理是 .
2.)如图,在△ABC中,AB=AC,点D为BC 的中点,AE是∠BAC外角的平分线,DE∥AB交AE于点E,则四边形ADCE的形状是 .
3.如图,在菱形ABCD中,对角线AC与BD交于点O,DE∥AC,CE∥BD.求证:四边形OCED是矩形.
知识点二:对角线相等的平行四边形是矩形
4.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC是矩形.
知识点三:有三个角是直角的四边形是矩形
5.(1)如图①,在Rt△ABC中,∠ACB=90°,点E,F分别是AC,BC的中点,D是斜边AB上一点,则添加下列条件可以使四边形DECF成为矩形的是( )
A.∠ACD=∠BCD B.AD=BD C.CD⊥AB D.CD=AC
(2)如图②,D,E,F分别是△ABC各边中点,则以下说法错误的是( )
A.△BDE和△DCF的面积相等 B.四边形AEDF是平行四边形
C.若AB=BC,则四边形AEDF是菱形 D.若∠A=90°,则四边形AEDF是矩形
6.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB∥DC B.AC=BD
C.AC⊥BD D.AB=DC
能力提升
7.如图,在△ABC中,分别取AB,AC的中点D,E,连接DE,过点A作AF⊥DE,垂足为点F,将△ADF,△AEF分别绕点D,E旋转180°,拼接成四边形BCHG,连接BH.若DE=4,AF=6,则BH的长度为 .
8.如图,在菱形ABCD中,E,F,G分别是AD,AB,CD的中点,且FG=5cm,EF=3cm,则菱形ABCD的面积是 cm .
9.如图,AB∥CD,点E,F分别在AB,CD上,连接EF.∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.求证:四边形EGFH是矩形.
10.如图①,在 ABCD中,连接对角线BD,过点A,C分别作AE⊥BD,CF⊥BD,垂足为点E,F.
(1)求证:AE=CF.
(2)如图②,延长AE至点G,使得AE=GE,连接CG,求证:四边形EGCF是矩形.
培优创新
11.如图,在△ABC中,AB=AC,点D在BC上,以AD,AE为腰作等腰△ADE,且∠ADE=∠ABC,连接CE,过点E作EF∥BC交CA的延长线于点F,连接BF.
(1)求证:∠ECA=∠ABC.
(2)如果AF=AB,求证:四边形FBDE是矩形.
参考答案
1.(2)平行四边 两组对边分别相等的四边形是平行四边形(3)矩 有一个角是直角的平行四边形是矩形
2.矩形
3.证明:∵CE∥BD,DE∥AC,∴四边形OCED是平行四边形.
∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°,∴四边形OCED是矩形.
4.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AD=BC,∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,∴EB=EC,∴△ABE≌△FCE(AAS),∴AB=CF.
∵AB∥CF,∴四边形ABFC是平行四边形.
∵AD=BC,AD=AF,∴BC=AF,∴四边形ABFC是矩形.
5.( 1)B ( 2)C 6.C 7.10
8.24 如图,连接AC,BD,交点为O,EF与AC交于点M,EG与BD交于点N.
∵四边形ABCD是菱形,∴AC⊥BD.
∵E,F,G分别是AD,AB,CD的中点,∴EF∥∥
∴四边形OMEN是矩形,∴∠FEG=90°.
∵FG=5cm,EF=3cm,∴EG=∴
∴菱形ABCD的面积 24(cm ).
9.证明:∵EH平分
平分
∥ ∴∠BEF+∠DFE=180°,∴∠FEH+∠EFH =
∵∠FEH+∠EFH+∠EHF=180°,∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°.
同理可得∠EGF=90°.
∵EG平分
∵EH平分
∵点A,E,B在同一条直线上,∴∠AEB=180°,即∠AEF+∠BEF=180°,
90°,即∠GEH=90°,
∴四边形EGFH是矩形.
10.证明:(1)∵四边形ABCD为平行四边形,∴AB∥CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD = 90°.
在△ABE和△CDF中, CF.
(2)由(1)得AE=CF.∵AE=GE,∴GE=CF.
∵AE⊥BD,CF⊥BD,∴AE∥CF,即EG∥CF,∴四边形EGCF是平行四边形.
∵AE⊥DB,∴∠DEG=90°,∴四边形EGCF是矩形.
11.证明:(1)∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°-2∠ABC.
同理,∠DAE=180°-2∠ADE.
∵∠ABC=∠ADE,∴∠BAC=∠DAE,∴∠BAD=∠CAE.
又∵AB=AC,AD=AE,∴△ABD≌△ACE (SAS),∴∠ECA=∠ABC.
(2)∵∠ECA=∠ABC,∠ABC=∠ACB,∴∠ECF=∠ACB.
∵EF∥BC,∴∠EFC=∠ACB,∴∠EFC=∠ECF,∴EF=EC.
∵△ABD≌△ACE,∴BD=EC,∴BD=EF,∴四边形FBDE是平行四边形.
∵AF=AB=AC,∴∠AFB=∠ABF,∠ABC=∠ACB.
∵∠AFB+∠ABF+∠ABC +∠ACB=180°,∴∠ABF+∠ABC=90°,即∠CBF=90°,
∴四边形FBDE是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
