6.2矩形的性质与判定 第3课时 矩形的性质与判定的综合应用 同步练习(含答案)
文档属性
| 名称 | 6.2矩形的性质与判定 第3课时 矩形的性质与判定的综合应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 12:30:32 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
2 矩形的性质与判定
第3课时 矩形的性质与判定的综合应用
基础闯关
知识点一:矩形性质与判定的综合应用
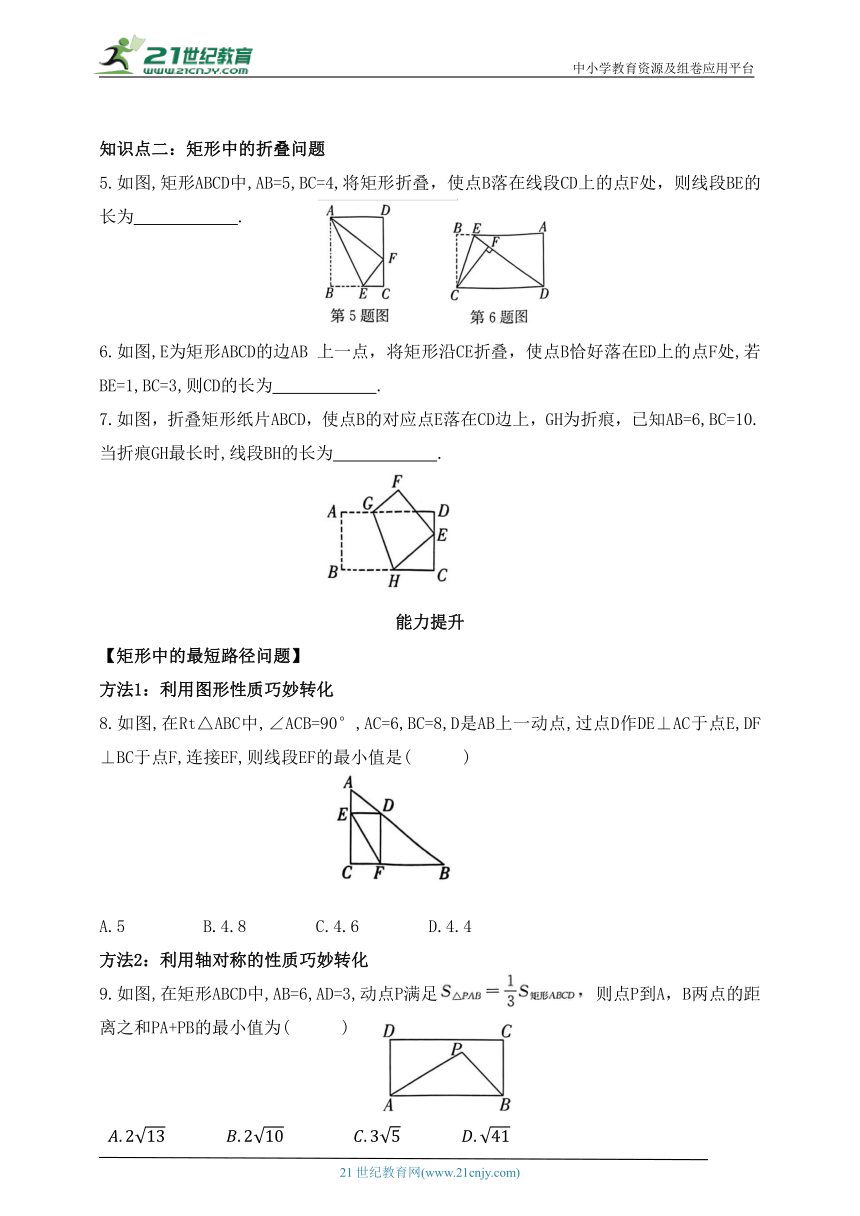
1.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE 的长为( )
A.10 B.8 C.6 D.4
2.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD,交BC于点E,若∠CAE=15°,则∠OBE的度数为 .
3.(株洲中考)如图所示,线段BC为等腰△ABC的底边,矩形ADBE 的对角线AB与DE交于点O,若OD=2,则AC= .
4.如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,AC=2,BC=3.点E是BC延长线上一点,且CE=3,连接DE.
(1)求证:四边形ACED为矩形.
(2)连接OE,求OE的长.
知识点二:矩形中的折叠问题
5.如图,矩形ABCD中,AB=5,BC=4,将矩形折叠,使点B落在线段CD上的点F处,则线段BE的长为 .
6.如图,E为矩形ABCD的边AB 上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为 .
7.如图,折叠矩形纸片ABCD,使点B的对应点E落在CD边上,GH为折痕,已知AB=6,BC=10.当折痕GH最长时,线段BH的长为 .
能力提升
【矩形中的最短路径问题】
方法1:利用图形性质巧妙转化
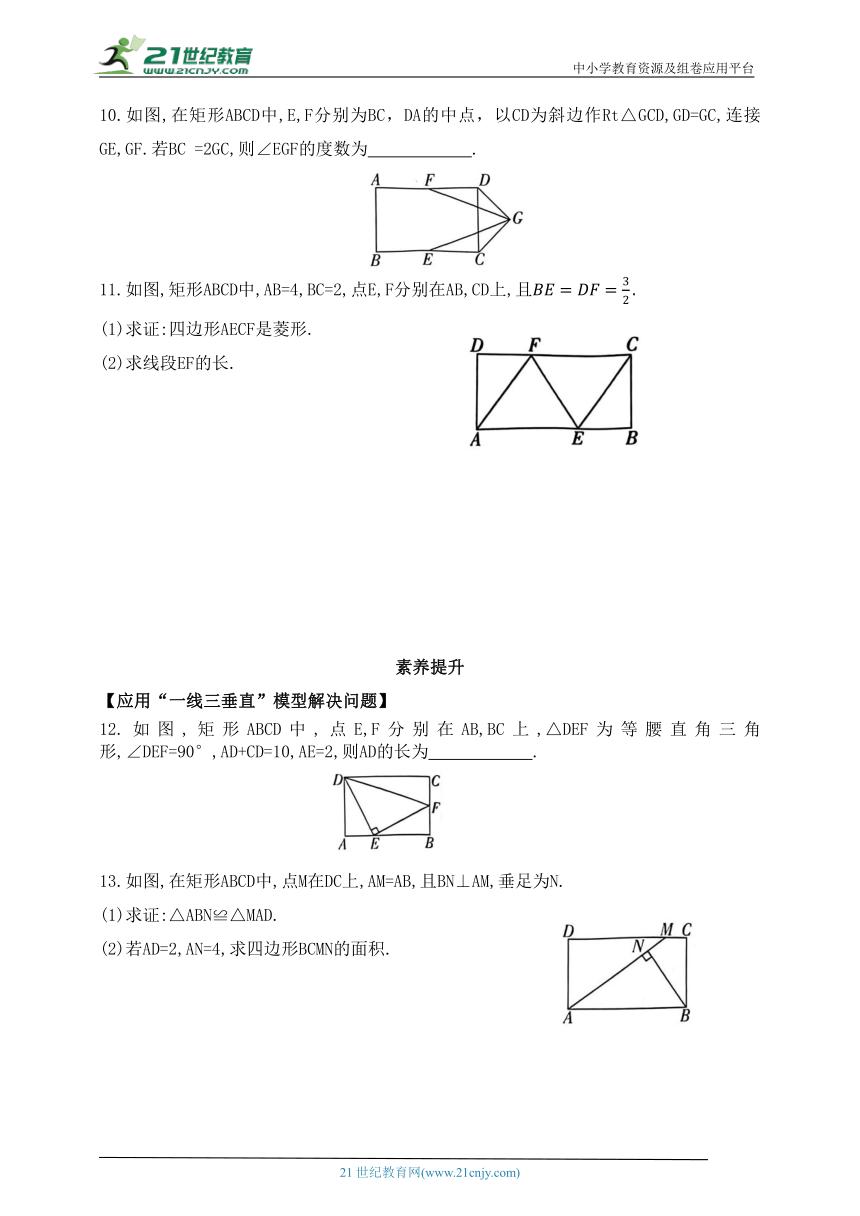
8.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
A.5 B.4.8 C.4.6 D.4.4
方法2:利用轴对称的性质巧妙转化
9.如图,在矩形ABCD中,AB=6,AD=3,动点P满足 则点P到A,B两点的距离之和PA+PB的最小值为( )
10.如图,在矩形ABCD中,E,F分别为BC,DA的中点,以CD为斜边作Rt△GCD,GD=GC,连接GE,GF.若BC =2GC,则∠EGF的度数为 .
11.如图,矩形ABCD中,AB=4,BC=2,点E,F分别在AB,CD上,且
(1)求证:四边形AECF是菱形.
(2)求线段EF的长.
素养提升
【应用“一线三垂直”模型解决问题】
12.如图,矩形ABCD中,点E,F分别在AB,BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,则AD的长为 .
13.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD.
(2)若AD=2,AN=4,求四边形BCMN的面积.
培优创新
14.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作BC的垂线,垂足为点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形.
(2)连接OE,若AB=13,OE=5,求AE 的长.
参考答案
1.B 2.30° 3.4
4.(1)证明:在□ABCD中,AD=BC=3,AD∥BC.∵CE=3,∴AD=CE,∴四边形ACED是平行四边形.∵AC⊥BC,∴∠ACE=90°,∴四边形ACED为矩形.
(2)解:
5.2.5 6.5
7.6.8 [解析]由题知,当E点与D点重合时,GH最长.设BH=x,则CH=10-x,HE=BH=x.由勾股定理得HC +CE =HE ,即( 10-x) +6 =x , 解得x=6.8.
8.B
9.A [解析]设△ABP中AB边上的高是h.
∴动点P在与AB平行且与AB的距离是2的直线l上.
如图,作点A关于直线l的对称点E,连接BE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=6,AE=2+2
即PA+PB的最小值为
10.45° [解析]∵以CD为斜边作Rt△GCD,GD=GC,∴∠GDC=∠GCD=45°,∠DGC=90°,
∴∠FDG=∠FDC+∠GDC=90°+45°=135°.
∵E,F分别为BC,DA的中点,BC=2GC,∴DF=DG,CE=CG,
∴∠DGF
同理可得∠CEG=∠CGE=22.5°,
∴∠EGF=∠DGC-∠DGF-∠CGE=90°-22.5°-22.5°=45°.
11.(1)证明:∵在矩形ABCD中,AB=4,BC=2,∴CD=AB=4,AD=BC=2,CD∥AB,∠D=∠B=90°.
∵BE=
∴四边形AECF是菱形.
(2)解:如图,过点F作FH⊥AB于点H,则四边形AHFD是矩形,
12.4
13.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,∴∠BAN=∠AMD.
∵BN⊥AM,∴∠BNA=90°.
在△ABN和△MAD中, ≌△MAD(AAS).
(2)解:∵△ABN≌△MAD,∴BN=AD.
∵AD=2,∴BN=2.在Rt△ABN中,∵AN=4,
14.(1)证明:∵四边形ABCD是菱形,∴AD∥BC且AD=BC.
∵BE=CF,∴BC=EF,∴AD=EF.
∵AD∥EF,∴四边形AEFD是平行四边形.
∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形.
(2)解:∵四边形ABCD 是菱形,∴AC⊥BD,AO=CO,BC=AB=13.
∵AE⊥BC,∴∠AEB=∠AEC=90°,∴AC=2OE=10.
∵AB -BE =AC -CE =AE ∴13 -BE =10 -(13-
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
2 矩形的性质与判定
第3课时 矩形的性质与判定的综合应用
基础闯关
知识点一:矩形性质与判定的综合应用
1.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE 的长为( )
A.10 B.8 C.6 D.4
2.如图,在矩形ABCD中,AC,BD相交于点O,AE平分∠BAD,交BC于点E,若∠CAE=15°,则∠OBE的度数为 .
3.(株洲中考)如图所示,线段BC为等腰△ABC的底边,矩形ADBE 的对角线AB与DE交于点O,若OD=2,则AC= .
4.如图,在 ABCD中,对角线AC,BD交于点O,AC⊥BC,AC=2,BC=3.点E是BC延长线上一点,且CE=3,连接DE.
(1)求证:四边形ACED为矩形.
(2)连接OE,求OE的长.
知识点二:矩形中的折叠问题
5.如图,矩形ABCD中,AB=5,BC=4,将矩形折叠,使点B落在线段CD上的点F处,则线段BE的长为 .
6.如图,E为矩形ABCD的边AB 上一点,将矩形沿CE折叠,使点B恰好落在ED上的点F处,若BE=1,BC=3,则CD的长为 .
7.如图,折叠矩形纸片ABCD,使点B的对应点E落在CD边上,GH为折痕,已知AB=6,BC=10.当折痕GH最长时,线段BH的长为 .
能力提升
【矩形中的最短路径问题】
方法1:利用图形性质巧妙转化
8.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
A.5 B.4.8 C.4.6 D.4.4
方法2:利用轴对称的性质巧妙转化
9.如图,在矩形ABCD中,AB=6,AD=3,动点P满足 则点P到A,B两点的距离之和PA+PB的最小值为( )
10.如图,在矩形ABCD中,E,F分别为BC,DA的中点,以CD为斜边作Rt△GCD,GD=GC,连接GE,GF.若BC =2GC,则∠EGF的度数为 .
11.如图,矩形ABCD中,AB=4,BC=2,点E,F分别在AB,CD上,且
(1)求证:四边形AECF是菱形.
(2)求线段EF的长.
素养提升
【应用“一线三垂直”模型解决问题】
12.如图,矩形ABCD中,点E,F分别在AB,BC上,△DEF为等腰直角三角形,∠DEF=90°,AD+CD=10,AE=2,则AD的长为 .
13.如图,在矩形ABCD中,点M在DC上,AM=AB,且BN⊥AM,垂足为N.
(1)求证:△ABN≌△MAD.
(2)若AD=2,AN=4,求四边形BCMN的面积.
培优创新
14.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作BC的垂线,垂足为点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形.
(2)连接OE,若AB=13,OE=5,求AE 的长.
参考答案
1.B 2.30° 3.4
4.(1)证明:在□ABCD中,AD=BC=3,AD∥BC.∵CE=3,∴AD=CE,∴四边形ACED是平行四边形.∵AC⊥BC,∴∠ACE=90°,∴四边形ACED为矩形.
(2)解:
5.2.5 6.5
7.6.8 [解析]由题知,当E点与D点重合时,GH最长.设BH=x,则CH=10-x,HE=BH=x.由勾股定理得HC +CE =HE ,即( 10-x) +6 =x , 解得x=6.8.
8.B
9.A [解析]设△ABP中AB边上的高是h.
∴动点P在与AB平行且与AB的距离是2的直线l上.
如图,作点A关于直线l的对称点E,连接BE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=6,AE=2+2
即PA+PB的最小值为
10.45° [解析]∵以CD为斜边作Rt△GCD,GD=GC,∴∠GDC=∠GCD=45°,∠DGC=90°,
∴∠FDG=∠FDC+∠GDC=90°+45°=135°.
∵E,F分别为BC,DA的中点,BC=2GC,∴DF=DG,CE=CG,
∴∠DGF
同理可得∠CEG=∠CGE=22.5°,
∴∠EGF=∠DGC-∠DGF-∠CGE=90°-22.5°-22.5°=45°.
11.(1)证明:∵在矩形ABCD中,AB=4,BC=2,∴CD=AB=4,AD=BC=2,CD∥AB,∠D=∠B=90°.
∵BE=
∴四边形AECF是菱形.
(2)解:如图,过点F作FH⊥AB于点H,则四边形AHFD是矩形,
12.4
13.(1)证明:在矩形ABCD中,∠D=90°,DC∥AB,∴∠BAN=∠AMD.
∵BN⊥AM,∴∠BNA=90°.
在△ABN和△MAD中, ≌△MAD(AAS).
(2)解:∵△ABN≌△MAD,∴BN=AD.
∵AD=2,∴BN=2.在Rt△ABN中,∵AN=4,
14.(1)证明:∵四边形ABCD是菱形,∴AD∥BC且AD=BC.
∵BE=CF,∴BC=EF,∴AD=EF.
∵AD∥EF,∴四边形AEFD是平行四边形.
∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形.
(2)解:∵四边形ABCD 是菱形,∴AC⊥BD,AO=CO,BC=AB=13.
∵AE⊥BC,∴∠AEB=∠AEC=90°,∴AC=2OE=10.
∵AB -BE =AC -CE =AE ∴13 -BE =10 -(13-
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
