北师大版九年级上册数学 4.9图形的相似 回顾与思考 课件 (共17张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 4.9图形的相似 回顾与思考 课件 (共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 869.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 15:48:16 | ||
图片预览



文档简介
(共17张PPT)
相似三角形复习
[课前预习题]
(1)△ABC∽△A’B’C’
(2)△ABC∽△A’C’B’
(3)△ABC∽△C’ A’ B’
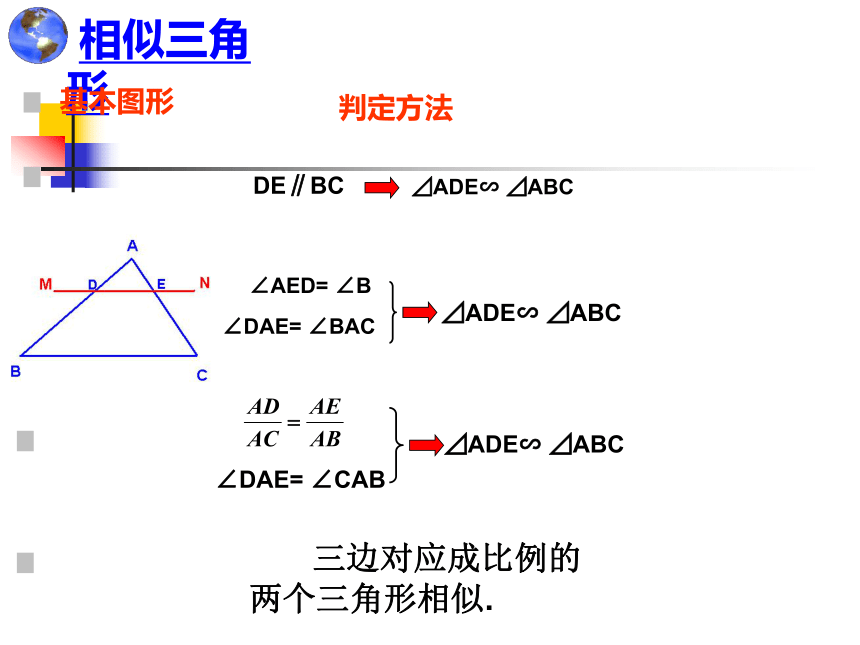
相似三角形
DE∥BC
⊿ADE∽ ⊿ABC
∠DAE= ∠CAB
⊿ADE∽ ⊿ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
⊿ADE∽ ⊿ABC
三边对应成比例的
两个三角形相似.
相似三角形
DE∥BC
⊿ADE∽ ⊿ABC
∠DAE= ∠CAB
⊿ADE∽ ⊿ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
⊿ADE∽ ⊿ABC
对应角相等;
性质定理
对应边成比例;
周长的比
等于相似比;
面积的比等于
相似比的平方;
三边对应成比例的
两个三角形相似.
A
E
D
C
B
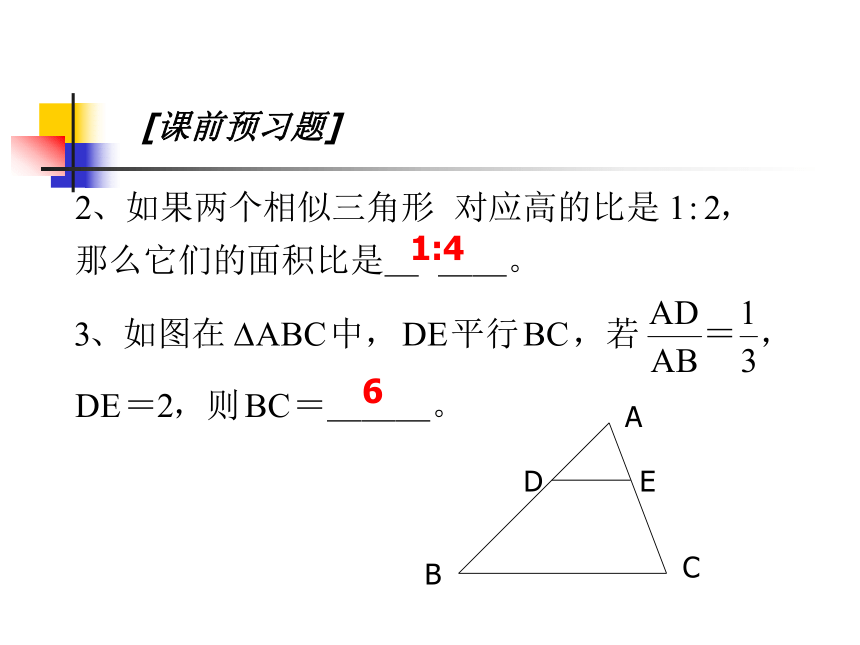
[课前预习题]
1:4
6
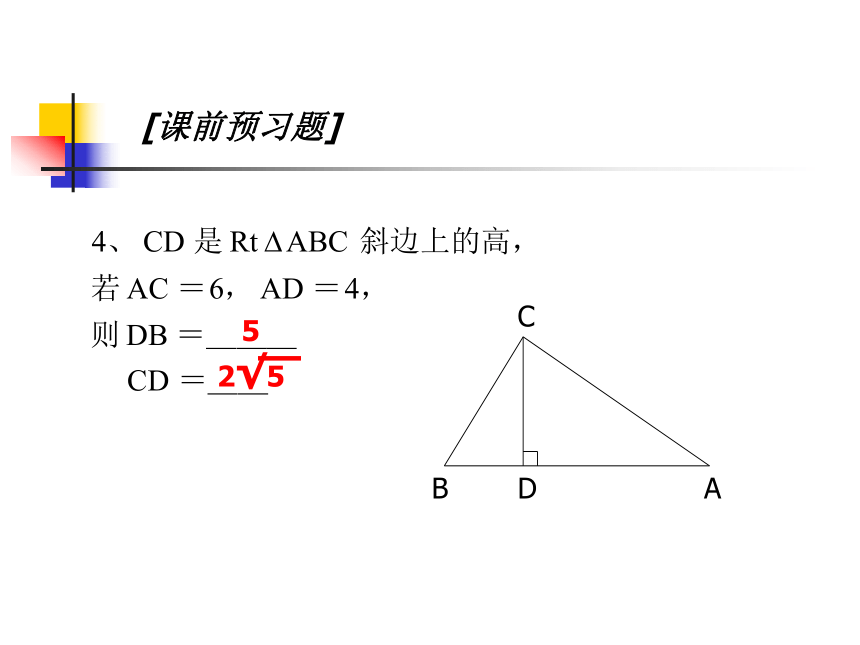
[课前预习题]
A
B
C
D
2√5
5
[课前预习题]
A
B
C
D
O
2:3
[动手操作一下]
(1)△DAE∽△DCA
(2)△DAE∽△ABE
(3)△DCA∽△ABE
[例题解析]
A
B
C
D
P
[做一做,你能行]
A
B
C
D
P
相似三角形
B
C
F
A
.
O
BC是圆O的切线,切点为C.
(1) ⊿BCF与⊿BAC相似吗
(2) 若BC=6,AF=5,你能求出BF的长吗
(3) 移动点A,使AC成为⊙O的直径,你还能
得到哪些结论
E
F
B
C
A
.
O
F
B
C
A
若∠ACB=90°,CF⊥AB,
则⊿ACF∽ ⊿ABC∽ ⊿CBF
⊿BCF∽ ⊿BAC
当∠BCF= ∠A 时,
⊿BCF∽ ⊿BAC.
F
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
(1)请在x轴上找一点D,使得⊿BDA与⊿BAC相似
(不包含全等),并求出点D的坐标;
(2)在(1)的条件下,如果P、Q分别是BA、BD上
的动点,连结PQ,设BP=DQ=m,
问:是否存在这样的m,使得⊿BPQ与⊿BDA相似?
如存在,请求出m的值;若不存在,请说明理由。
用一用
O
D
(1)∵⊿BDA∽⊿BAC
∴∠CAD=∠ABC
∴tan∠CAD=∠ABC=
∵BC=4
∴AC=BC·tan ∠ABC=3
∴CD=AC·tan ∠CAD=3× =
∴OD=OC+CD=1+ =
∴D( ,0)
用一用
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
O
D
用一用
P
Q
P
Q
(1)当PQ∥AD时,⊿BPQ∽ ⊿BAD
则
即:
解得:
(2)当PQ⊥BD时,⊿BPQ∽ ⊿BDA
则
即:
解得:
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
O
D
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
O
D
[探索与思考]
D
A
B
C
E
F
再见
相似三角形复习
[课前预习题]
(1)△ABC∽△A’B’C’
(2)△ABC∽△A’C’B’
(3)△ABC∽△C’ A’ B’
相似三角形
DE∥BC
⊿ADE∽ ⊿ABC
∠DAE= ∠CAB
⊿ADE∽ ⊿ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
⊿ADE∽ ⊿ABC
三边对应成比例的
两个三角形相似.
相似三角形
DE∥BC
⊿ADE∽ ⊿ABC
∠DAE= ∠CAB
⊿ADE∽ ⊿ABC
基本图形
判定方法
∠AED= ∠B
∠DAE= ∠BAC
⊿ADE∽ ⊿ABC
对应角相等;
性质定理
对应边成比例;
周长的比
等于相似比;
面积的比等于
相似比的平方;
三边对应成比例的
两个三角形相似.
A
E
D
C
B
[课前预习题]
1:4
6
[课前预习题]
A
B
C
D
2√5
5
[课前预习题]
A
B
C
D
O
2:3
[动手操作一下]
(1)△DAE∽△DCA
(2)△DAE∽△ABE
(3)△DCA∽△ABE
[例题解析]
A
B
C
D
P
[做一做,你能行]
A
B
C
D
P
相似三角形
B
C
F
A
.
O
BC是圆O的切线,切点为C.
(1) ⊿BCF与⊿BAC相似吗
(2) 若BC=6,AF=5,你能求出BF的长吗
(3) 移动点A,使AC成为⊙O的直径,你还能
得到哪些结论
E
F
B
C
A
.
O
F
B
C
A
若∠ACB=90°,CF⊥AB,
则⊿ACF∽ ⊿ABC∽ ⊿CBF
⊿BCF∽ ⊿BAC
当∠BCF= ∠A 时,
⊿BCF∽ ⊿BAC.
F
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
(1)请在x轴上找一点D,使得⊿BDA与⊿BAC相似
(不包含全等),并求出点D的坐标;
(2)在(1)的条件下,如果P、Q分别是BA、BD上
的动点,连结PQ,设BP=DQ=m,
问:是否存在这样的m,使得⊿BPQ与⊿BDA相似?
如存在,请求出m的值;若不存在,请说明理由。
用一用
O
D
(1)∵⊿BDA∽⊿BAC
∴∠CAD=∠ABC
∴tan∠CAD=∠ABC=
∵BC=4
∴AC=BC·tan ∠ABC=3
∴CD=AC·tan ∠CAD=3× =
∴OD=OC+CD=1+ =
∴D( ,0)
用一用
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
O
D
用一用
P
Q
P
Q
(1)当PQ∥AD时,⊿BPQ∽ ⊿BAD
则
即:
解得:
(2)当PQ⊥BD时,⊿BPQ∽ ⊿BDA
则
即:
解得:
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
O
D
B
C
A
x
y
(-3,0)
(1,0)
tan∠ABC=
O
D
[探索与思考]
D
A
B
C
E
F
再见
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
