【班海精品】北师大版(新)八年级下-1.3线段的垂直平分线 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-1.3线段的垂直平分线 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 15:34:56 | ||
图片预览








文档简介
(共44张PPT)
3.线段的垂直平分线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
线段的垂直平分线的性质与判定的内容是什么?
复
习
回
顾
新课精讲
探索新知
1
知识点
三角形三边垂直平分线的性质
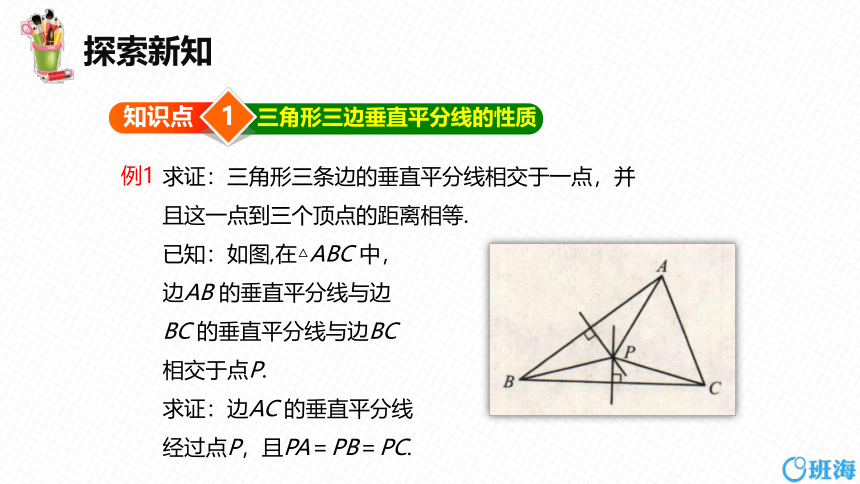
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC 中,
边AB 的垂直平分线与边
BC 的垂直平分线与边BC
相交于点P.
求证:边AC 的垂直平分线
经过点P,且PA=PB=PC.
例1
探索新知
∵点P 在线段AB 的垂直平分线上,
∴ PA = PB (线段垂直平分线上的点到这条线段
两个端点的距离相等).
同理,PB =PC.
∴点P 在线段AC 的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
即边AC 的垂直平分线经过点P.
证明:
探索新知
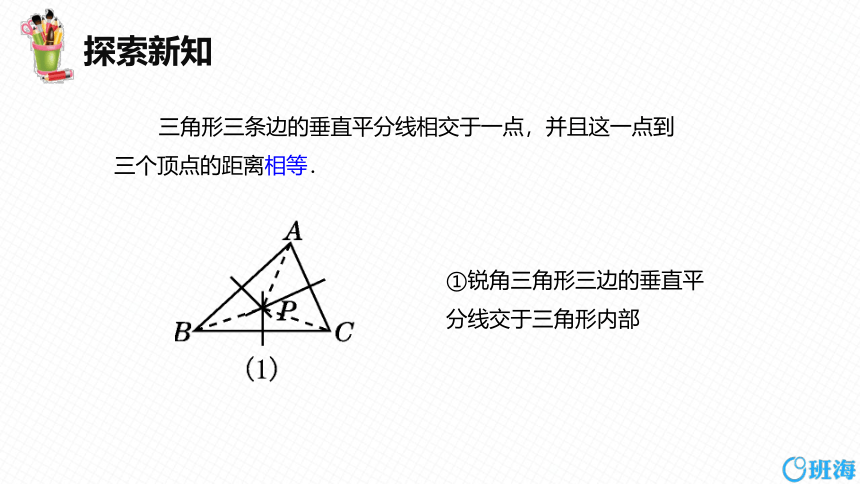
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
①锐角三角形三边的垂直平分线交于三角形内部
探索新知
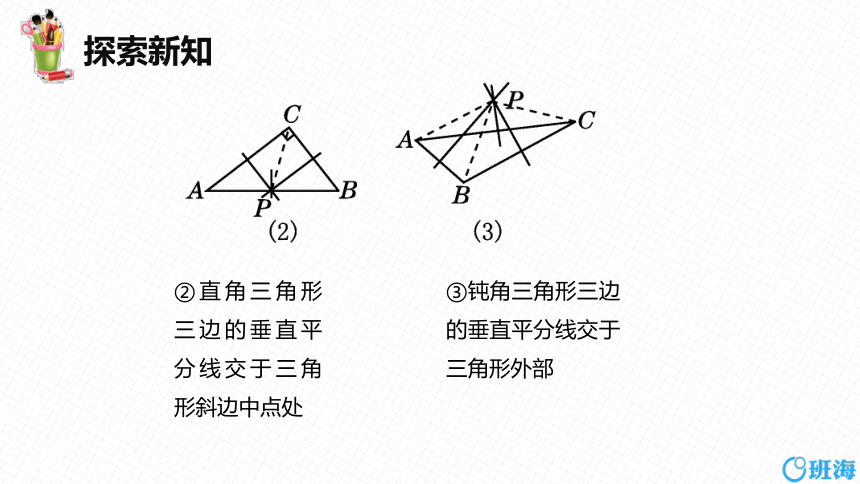
③钝角三角形三边的垂直平分线交于三角形外部
②直角三角形三边的垂直平分线交于三角形斜边中点处
探索新知
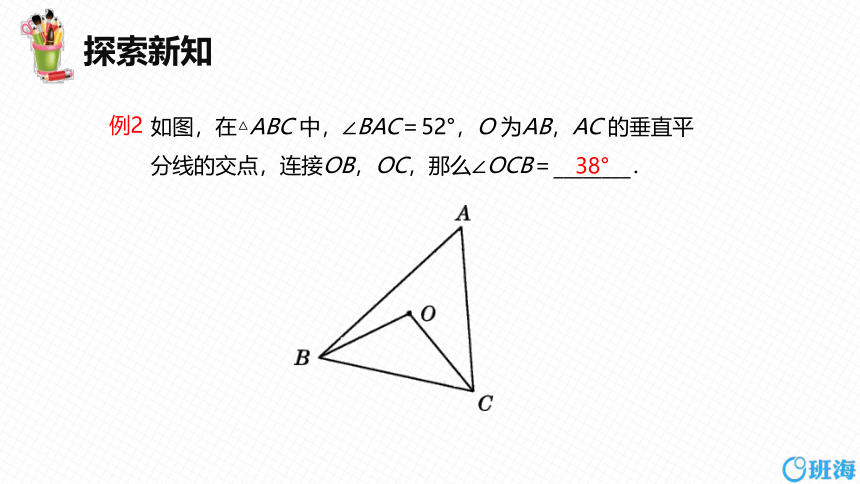
如图,在△ABC 中,∠BAC=52°,O 为AB,AC 的垂直平分线的交点,连接OB,OC,那么∠OCB=________.
例2
38°
探索新知
导引:
如图,连接OA,
∵O 为AB,AC 的垂直平分线的交点,
∴ OA=OB=OC.
∴∠1=∠2,∠3=∠4,∠5=∠6.
∴∠1+∠4=∠2+∠3=∠BAC=52°.
∴∠5+∠6=180°-(∠1+∠2+∠3+
∠4)=180°-2×52°=76°.
∴∠6= ×76°=38°,
即∠OCB=38°.
探索新知
总 结
此类题的一般规律是:若O 为△ABC (锐角三角形)三边垂直平分线的交点,则有∠BOC=2∠A,∠OCB=∠OBC=∠90°-∠A.
典题精讲
1
如图,在△ABC 中,BC=2,∠BAC >90°,AB 的垂直平分线交BC 于点E,AC 的垂直平分线交BC 于点F,请找出图中相等的线段,并求△AEF 的周长.
BE=AE,AF=CF.
△AEF 的周长为AE+EF+AF
=BE+EF+FC=BC=2.
解:
典题精讲
2
三角形三边的垂直平分线的交点( )
A.到三角形三边的距离相等
B.到三角形三个顶点的距离相等
C.到三角形三个顶点与三条边的距离相等
D.不能确定
B
典题精讲
3
在联欢晚会上,三名同学站在一个非等边三角形的三个顶点A,B,C 位置上,他们在玩抢凳子游戏,要求在他们中间放一个凳子,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最适当的位置是△ABC 的( )
A.三边上的中线的交点
B.三条角平分线的交点
C.三边上的高线的交点
D.三边垂直平分线的交点
D
典题精讲
4
如图,D 是线段AC,AB 的垂直平分线的交点,若∠ACD=30°,∠BAD=50°,则∠BCD 的大小是( )
A.10°
B.20°
C.30°
D.40°
A
探索新知
2
知识点
与线段垂直平分线相关的作图
议一议
(1)已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能画出几个?所画出的三角形都全等吗?
(2)已知等腰三角形的底边及底边上的高,你能用尺规作出满足条件的一个等腰三角形吗?
探索新知
用尺规作已知线段的垂直平分线的方法:
已知:线段AB (如图).
求作:线段AB 的垂直平分线.
作法:①分别以点A 和点B 为圆心,
以大于 AB 的长为半径画弧,
两弧相交于点C 和点D.
②作直线CD,直线CD 就是线段
AB 的垂直平分线(如图).
探索新知
已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.
已知:如图 (1),线段a,h.
求做:△ABC,使AB=AC,且BC=a,高 AD=h.
例3
a
h
(1)
探索新知
作法:
(1)作线段BC=a (如图(2)).
(2)作线段BC 的垂直平分线l,
交BC 于点D.
(3) 在l 上作线段DA 使DA=h.
(4)连接AB,AC.
△ABC 为所求的等腰三角形.
A
B
C
D
l
×
×
探索新知
如图,河流AB 的一旁有一村庄P,现要在河流上修建供水站向村庄P 供水,要使供水路径最短,求作供水站M 的位置.
例4
探索新知
解:
如图,作法:①以P 为圆心,以适当的长度为半
径画弧,交直线AB 于C,D 两点.
②作线段CD 的垂直平分线MN,交CD 于M,M点
就是所求作的点.
探索新知
总 结
直线外一点到直线上各点所连的所有线段中,垂线段最短.
典题精讲
1
如图,已知钝角三角形ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C 为圆心,CA 为半径画弧①;
步骤2:以B 为圆心,BA 为半径画弧②,
交弧①于点D;
步骤3:连接AD,交BC 的延长线于点H.
下列叙述正确的是( )
A.BH 垂直平分线段AD B.AC 平分∠BAD
C.S△ABC=BC · AH D.AB=AD
A
典题精讲
2
已知△ABC,AB<BC,用尺规作图的方法在BC 上取一点P,使得PA+PC=BC,则下列选项正确的是( )
D
典题精讲
3
如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h. 张红的作法是:
(1)作线段BC=a;
(2)作线段BC 的垂直平分线MN,
MN 与BC 相交于点D;
(3)在直线MN 上截取线段h;
(4)连接AB,AC. △ABC 为所求
作的等腰三角形.
上述作法的四个步骤中,有错误的一步你认为是( )
A.(1) B.(2) C.(3) D.(4)
C
易错提醒
等腰三角形的顶角为100°,其中两边的垂直平分线交于点P,则点P 在( )
A.三角形底边上
B.三角形内
C.三角形外
D.点P 的位置与三角形边长有关
易错点:三角形三边垂直平分线交点不一定在三角形内部
C
学以致用
小试牛刀
1
如图,在△ABC 中,分别以点A 和点B 为圆心,大于 AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC 于点D,连接AD. 若△ADC 的周长为10,AB=7,则△ABC 的周长为( )
A.7
B.14
C.17
D.20
C
小试牛刀
2
如图,在△ABC 中,AB=AC,D 是BC 的中点,AC 的垂直平分线分别交AC,AD,AB 于点E,O,F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
D
小试牛刀
3 如图,在△ABC 中,边AB,BC 的垂直平分线交于点P.
(1)求证:PA=PB=PC.
(2)点P 在边AC 的垂直平分线上吗?请说明理由.
小试牛刀
∵点P 是边AB,BC 的垂直平分线的交点,∴PA=PB,PB=PC.
∴PA=PB=PC.
点P 在边AC 的垂直平分线上.
理由:∵PA=PC,
∴点P 在边AC 的垂直平分线上.
(1)证明:
(2)解:
小试牛刀
4 如图,在△ABC 中,∠C=60°,∠A=40°.
(1)用尺规作图:作AB 的垂直平分线,交AC 于点D,交AB 于点E (保留作图痕迹,不要求写作法和证明);
(2)求证:BD 平分∠CBA.
小试牛刀
如图①.
(1)解:
小试牛刀
连接BD,如图②所示,
∵∠C=60°,∠A=40°,
∴∠CBA=80°.
∵DE 是AB 的垂直平分线,
∴AD=BD.
∴∠A=∠DBA=40°.
∴∠DBA= ∠CBA.
∴BD 平分∠CBA.
(2)证明:
小试牛刀
5 如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)
小试牛刀
如图,直线AD 即为所求.
解:
小试牛刀
6 如图,一机器人在点A 处发现一个小球自点B 处沿x 轴向原点O 方向匀速滚去,机器人立即从A 处匀速直线前进,去截小球,若小球滚动速度与机器人行走速度相等.试在图中标出机器人恰好能截住小球的位置C. (保留作图痕迹)
小试牛刀
如图,连接AB,作线段AB 的垂直平分线,交x 轴于点C,C 点就是所求作的位置.
解:
小试牛刀
7 如图,在△ABC 中,D 为BC 的中点,E,F 分别是AB,AC 上的点,且DE⊥DF.
求证:BE+CF>EF.
小试牛刀
如图,延长ED 至点M,使DM=ED,
连接MC,MF,则EF=FM.
∵BD=CD,DE=DM,∠BDE=∠CDM,
∴△BDE ≌ △CDM (SAS).
∴BE=CM.
∵CF+CM>MF,
∴BE+CF>EF.
证明:
课堂小结
课堂小结
1.三角形三条边的垂直平分线交于同一点,这一点叫
做三角形的外心(三角形外接圆的圆心,以后即可学到).
2.几种三角形三条边的垂直平分线交点的位置情况:
(1)锐角三角形三边垂直平分线交于三角形内部;
(2)直角三角形三边垂直平分线交于三角形斜边中点;
(3)钝角三角形三边垂直平分线交于三角形外部.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.线段的垂直平分线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
线段的垂直平分线的性质与判定的内容是什么?
复
习
回
顾
新课精讲
探索新知
1
知识点
三角形三边垂直平分线的性质
求证:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
已知:如图,在△ABC 中,
边AB 的垂直平分线与边
BC 的垂直平分线与边BC
相交于点P.
求证:边AC 的垂直平分线
经过点P,且PA=PB=PC.
例1
探索新知
∵点P 在线段AB 的垂直平分线上,
∴ PA = PB (线段垂直平分线上的点到这条线段
两个端点的距离相等).
同理,PB =PC.
∴点P 在线段AC 的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),
即边AC 的垂直平分线经过点P.
证明:
探索新知
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
①锐角三角形三边的垂直平分线交于三角形内部
探索新知
③钝角三角形三边的垂直平分线交于三角形外部
②直角三角形三边的垂直平分线交于三角形斜边中点处
探索新知
如图,在△ABC 中,∠BAC=52°,O 为AB,AC 的垂直平分线的交点,连接OB,OC,那么∠OCB=________.
例2
38°
探索新知
导引:
如图,连接OA,
∵O 为AB,AC 的垂直平分线的交点,
∴ OA=OB=OC.
∴∠1=∠2,∠3=∠4,∠5=∠6.
∴∠1+∠4=∠2+∠3=∠BAC=52°.
∴∠5+∠6=180°-(∠1+∠2+∠3+
∠4)=180°-2×52°=76°.
∴∠6= ×76°=38°,
即∠OCB=38°.
探索新知
总 结
此类题的一般规律是:若O 为△ABC (锐角三角形)三边垂直平分线的交点,则有∠BOC=2∠A,∠OCB=∠OBC=∠90°-∠A.
典题精讲
1
如图,在△ABC 中,BC=2,∠BAC >90°,AB 的垂直平分线交BC 于点E,AC 的垂直平分线交BC 于点F,请找出图中相等的线段,并求△AEF 的周长.
BE=AE,AF=CF.
△AEF 的周长为AE+EF+AF
=BE+EF+FC=BC=2.
解:
典题精讲
2
三角形三边的垂直平分线的交点( )
A.到三角形三边的距离相等
B.到三角形三个顶点的距离相等
C.到三角形三个顶点与三条边的距离相等
D.不能确定
B
典题精讲
3
在联欢晚会上,三名同学站在一个非等边三角形的三个顶点A,B,C 位置上,他们在玩抢凳子游戏,要求在他们中间放一个凳子,谁先抢到凳子谁获胜,为使游戏公平,凳子应放的最适当的位置是△ABC 的( )
A.三边上的中线的交点
B.三条角平分线的交点
C.三边上的高线的交点
D.三边垂直平分线的交点
D
典题精讲
4
如图,D 是线段AC,AB 的垂直平分线的交点,若∠ACD=30°,∠BAD=50°,则∠BCD 的大小是( )
A.10°
B.20°
C.30°
D.40°
A
探索新知
2
知识点
与线段垂直平分线相关的作图
议一议
(1)已知三角形的一条边及这条边上的高,你能画出满足条件的三角形吗?如果能,能画出几个?所画出的三角形都全等吗?
(2)已知等腰三角形的底边及底边上的高,你能用尺规作出满足条件的一个等腰三角形吗?
探索新知
用尺规作已知线段的垂直平分线的方法:
已知:线段AB (如图).
求作:线段AB 的垂直平分线.
作法:①分别以点A 和点B 为圆心,
以大于 AB 的长为半径画弧,
两弧相交于点C 和点D.
②作直线CD,直线CD 就是线段
AB 的垂直平分线(如图).
探索新知
已知一个等腰三角形的底边及底边上的高,求作这个等腰三角形.
已知:如图 (1),线段a,h.
求做:△ABC,使AB=AC,且BC=a,高 AD=h.
例3
a
h
(1)
探索新知
作法:
(1)作线段BC=a (如图(2)).
(2)作线段BC 的垂直平分线l,
交BC 于点D.
(3) 在l 上作线段DA 使DA=h.
(4)连接AB,AC.
△ABC 为所求的等腰三角形.
A
B
C
D
l
×
×
探索新知
如图,河流AB 的一旁有一村庄P,现要在河流上修建供水站向村庄P 供水,要使供水路径最短,求作供水站M 的位置.
例4
探索新知
解:
如图,作法:①以P 为圆心,以适当的长度为半
径画弧,交直线AB 于C,D 两点.
②作线段CD 的垂直平分线MN,交CD 于M,M点
就是所求作的点.
探索新知
总 结
直线外一点到直线上各点所连的所有线段中,垂线段最短.
典题精讲
1
如图,已知钝角三角形ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C 为圆心,CA 为半径画弧①;
步骤2:以B 为圆心,BA 为半径画弧②,
交弧①于点D;
步骤3:连接AD,交BC 的延长线于点H.
下列叙述正确的是( )
A.BH 垂直平分线段AD B.AC 平分∠BAD
C.S△ABC=BC · AH D.AB=AD
A
典题精讲
2
已知△ABC,AB<BC,用尺规作图的方法在BC 上取一点P,使得PA+PC=BC,则下列选项正确的是( )
D
典题精讲
3
如图,已知线段a,h,作等腰三角形ABC,使AB=AC,且BC=a,BC边上的高AD=h. 张红的作法是:
(1)作线段BC=a;
(2)作线段BC 的垂直平分线MN,
MN 与BC 相交于点D;
(3)在直线MN 上截取线段h;
(4)连接AB,AC. △ABC 为所求
作的等腰三角形.
上述作法的四个步骤中,有错误的一步你认为是( )
A.(1) B.(2) C.(3) D.(4)
C
易错提醒
等腰三角形的顶角为100°,其中两边的垂直平分线交于点P,则点P 在( )
A.三角形底边上
B.三角形内
C.三角形外
D.点P 的位置与三角形边长有关
易错点:三角形三边垂直平分线交点不一定在三角形内部
C
学以致用
小试牛刀
1
如图,在△ABC 中,分别以点A 和点B 为圆心,大于 AB 的长为半径画弧,两弧相交于点M,N,作直线MN,交BC 于点D,连接AD. 若△ADC 的周长为10,AB=7,则△ABC 的周长为( )
A.7
B.14
C.17
D.20
C
小试牛刀
2
如图,在△ABC 中,AB=AC,D 是BC 的中点,AC 的垂直平分线分别交AC,AD,AB 于点E,O,F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
D
小试牛刀
3 如图,在△ABC 中,边AB,BC 的垂直平分线交于点P.
(1)求证:PA=PB=PC.
(2)点P 在边AC 的垂直平分线上吗?请说明理由.
小试牛刀
∵点P 是边AB,BC 的垂直平分线的交点,∴PA=PB,PB=PC.
∴PA=PB=PC.
点P 在边AC 的垂直平分线上.
理由:∵PA=PC,
∴点P 在边AC 的垂直平分线上.
(1)证明:
(2)解:
小试牛刀
4 如图,在△ABC 中,∠C=60°,∠A=40°.
(1)用尺规作图:作AB 的垂直平分线,交AC 于点D,交AB 于点E (保留作图痕迹,不要求写作法和证明);
(2)求证:BD 平分∠CBA.
小试牛刀
如图①.
(1)解:
小试牛刀
连接BD,如图②所示,
∵∠C=60°,∠A=40°,
∴∠CBA=80°.
∵DE 是AB 的垂直平分线,
∴AD=BD.
∴∠A=∠DBA=40°.
∴∠DBA= ∠CBA.
∴BD 平分∠CBA.
(2)证明:
小试牛刀
5 如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)
小试牛刀
如图,直线AD 即为所求.
解:
小试牛刀
6 如图,一机器人在点A 处发现一个小球自点B 处沿x 轴向原点O 方向匀速滚去,机器人立即从A 处匀速直线前进,去截小球,若小球滚动速度与机器人行走速度相等.试在图中标出机器人恰好能截住小球的位置C. (保留作图痕迹)
小试牛刀
如图,连接AB,作线段AB 的垂直平分线,交x 轴于点C,C 点就是所求作的位置.
解:
小试牛刀
7 如图,在△ABC 中,D 为BC 的中点,E,F 分别是AB,AC 上的点,且DE⊥DF.
求证:BE+CF>EF.
小试牛刀
如图,延长ED 至点M,使DM=ED,
连接MC,MF,则EF=FM.
∵BD=CD,DE=DM,∠BDE=∠CDM,
∴△BDE ≌ △CDM (SAS).
∴BE=CM.
∵CF+CM>MF,
∴BE+CF>EF.
证明:
课堂小结
课堂小结
1.三角形三条边的垂直平分线交于同一点,这一点叫
做三角形的外心(三角形外接圆的圆心,以后即可学到).
2.几种三角形三条边的垂直平分线交点的位置情况:
(1)锐角三角形三边垂直平分线交于三角形内部;
(2)直角三角形三边垂直平分线交于三角形斜边中点;
(3)钝角三角形三边垂直平分线交于三角形外部.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
