【班海精品】北师大版(新)八年级下-1.4角平分线 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-1.4角平分线 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览







文档简介
(共50张PPT)
4.角平分线
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
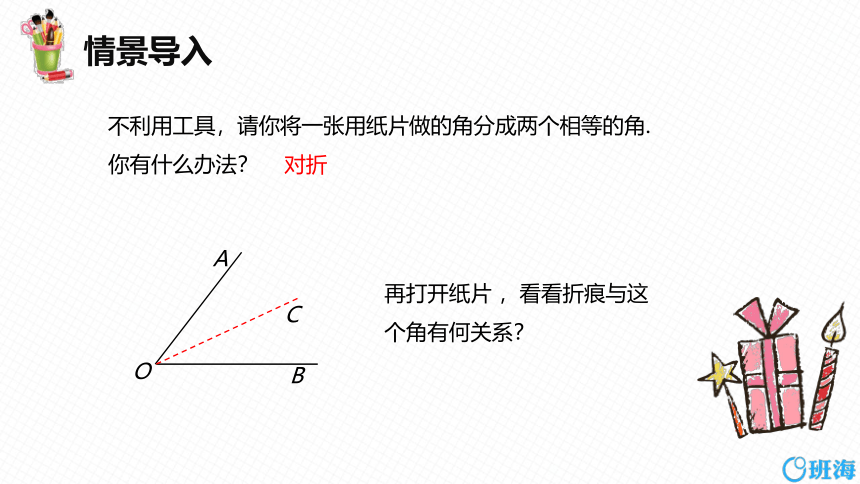
不利用工具,请你将一张用纸片做的角分成两个相等的角. 你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
新课精讲
探索新知
1
知识点
角平分线的性质
还记得角平分线上的点有什么性质吗?你是怎样得到的?请你尝试证明这性质,并与同伴交流.
A
B
O
P
C
D
E
探索新知
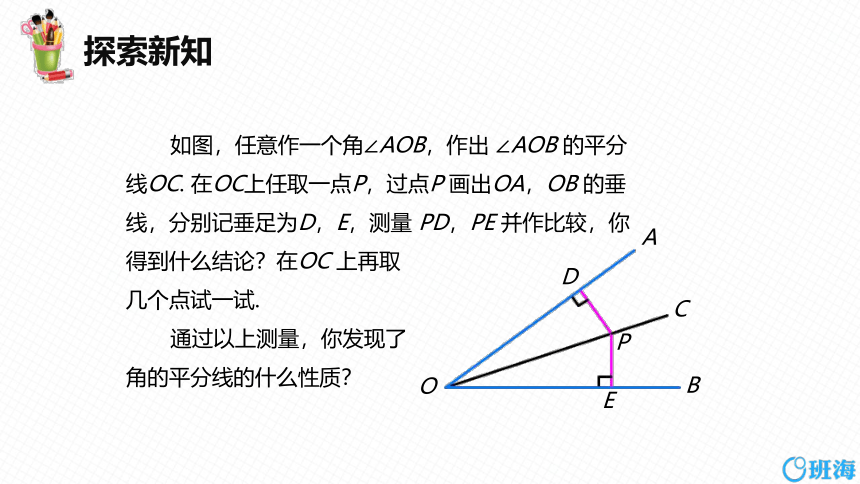
如图,任意作一个角∠AOB,作出 ∠AOB 的平分
线OC. 在OC上任取一点P,过点P 画出OA,OB 的垂
线,分别记垂足为D,E,测量 PD,PE 并作比较,你
得到什么结论?在OC 上再取
几个点试一试.
通过以上测量,你发现了
角的平分线的什么性质?
探索新知
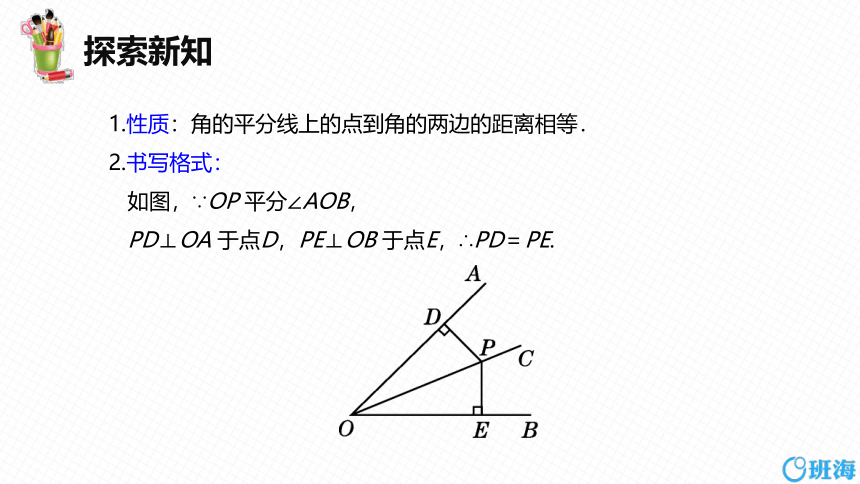
1.性质:角的平分线上的点到角的两边的距离相等.
2.书写格式:
如图,∵OP 平分∠AOB,
PD⊥OA 于点D,PE⊥OB 于点E,∴PD=PE.
探索新知
B
A
D
O
P
E
C
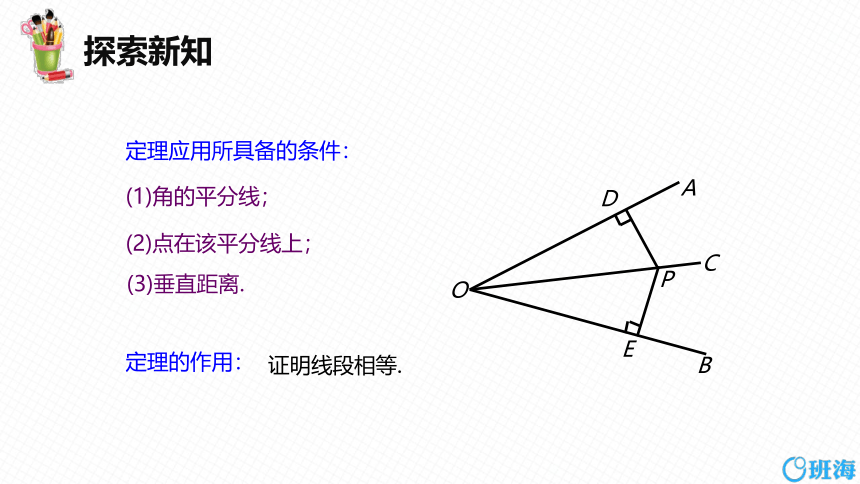
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
探索新知
归 纳
定理 角平分线上的点到这个角的两边的距离相等.
探索新知
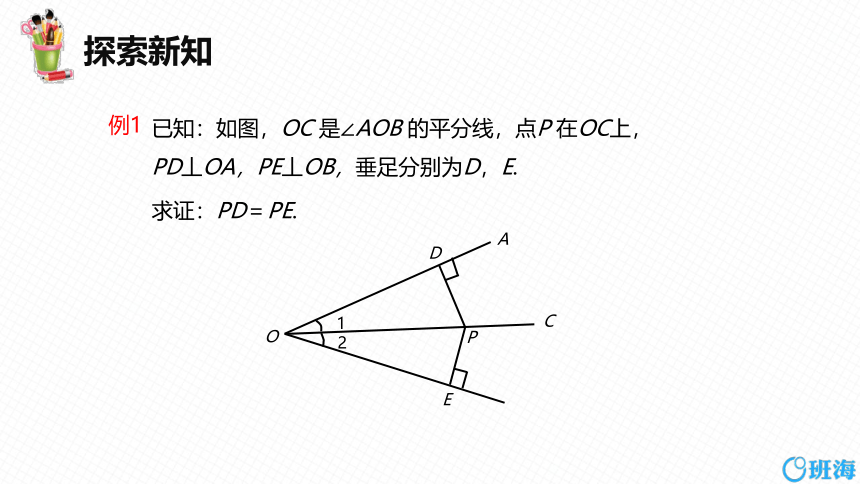
已知:如图,OC 是∠AOB 的平分线,点P 在OC上,PD丄OA,PE丄OB,垂足分别为D,E.
求证:PD=PE.
例1
O
D
A
C
E
P
1
2
探索新知
∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠PDO=∠PEO=90°.
∵∠1=∠2,OP=OP
∴△PDO ≌ △PEO ( AAS ).
∴PD=PE (全等三角形的对应边相等).
证明:
探索新知
例2
如图,在△ABC 中,∠BAC=60°,点D 在BC 上, AD=10,DE 丄AB, DF丄AC ,垂足分别为E,F,DE=DF,求DE 的长.
A
B
C
E
F
D
探索新知
解:
∵DE丄AB,DF丄AC,垂足分分别为E,F,
且DE=DF,
∴AD 平分∠BAC (在一个角的内部,到角的两边
距离相等的点在这个角的平分线上).
又∵∠BAC=60°,
∴∠BAD=30°.
在 Rt△ADE 中,∠AED=90°,AD=10,
∴DE= AD= ×10=5 (在直角三角形中,如果一个锐角等于30°. 那么它所对的直角边等于斜边的一半).
典题精讲
1
如图,AD,AE 分别是△ABC 中∠A 的内角平分线和外角平分线,它们有什么关系?
解:AD⊥AE.
C
D
B
A
E
F
典题精讲
2
如图,OP 是∠AOB 的平分线,点C,D 分别在角的两边OA,OB 上,添加下列条件,不能判定△POC ≌ △POD 的选项是( )
A.PC⊥OA,PD⊥OB
B.OC=OD
C.∠OPC=∠OPD
D.PC=PD
D
典题精讲
如图,OP 平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO 平分∠APB
C.OA=OB
D.AB 垂直平分OP
D
典题精讲
4
如图,点P 是∠AOB 平分线OC 上一点,PD⊥OB,垂足为D,若PD=2,则点P 到边OA 的距离是( )
A.2
B.3
C.
D.4
A
典题精讲
5
如图,在△ABC 中,∠C=90°,AC=BC,AD 平分∠CAB 交BC 于D,DE⊥AB 于E,若AB=6 cm,则△DBE 的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
探索新知
2
知识点
角平分线的判定
角平分线的性质:角的平分线上的点到角的两边的距离相等.
O
D
E
P
P 到OA 的距离
P 到OB 的距离
角平分线上的点
A
C
B
探索新知
如图,由 于点 D ,
于点E,PD = PE ,可
以得到什么结论 ?
OB
PE
⊥
PD
⊥
OA
B
A
D
O
P
E
到一个角的两边的距离相等的点, 在这个角的平分线上.
探索新知
证明过程:
已知:如图,点P 为∠AOB 内一点,PD丄OA,PE丄OB,垂足分别为D,E,且PD=PE.
求证:OP 平分∠AOB.
O
D
A
C
E
P
1
2
B
探索新知
∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠ODP=∠OEP=90°,
∵PD=PE,OP=OP,
∴Rt△DOP ≌ Rt△EOP ( HL ).
∴∠1=∠2 (全等三角形的对应角相等).
∴OP 平分∠AOB.
证明:
探索新知
判定方法:角的内部到角的两边的距离相等的点在角
的平分线上.
书写格式:如图,∵PD⊥OA,PE⊥OB,PD=PE, ∴点P 在∠AOB 的平分线上(或∠AOC=∠BOC ).
探索新知
如图,已知BE=CF,DF⊥AC 于点F,DE⊥AB 于点E,BF 和CE 相交于点D.
求证:AD 平分∠BAC.
例3
导引:
要证AD 平分∠BAC,已知条件
中有两个垂直,即有点到角的
两边的距离,再证这两个距离
相等即可证明结论,证这两条
垂线段相等,可通过证明
△BDE 和△CDF 全等来完成.
探索新知
∵DF⊥AC 于点F,DE⊥AB 于点E,
∴∠DEB=∠DFC=90°.
在△BDE 和△CDF 中,
∴△BDE ≌ △CDF (AAS).
∴DE=DF.
又∵DF⊥AC 于点F,DE⊥AB 于点E,
∴AD 平分∠BAC.
证明:
探索新知
总 结
判定角平分线有两步:
(1)找出与角的两边都垂直的垂线段;
(2)证明两条垂线段相等.
典题精讲
1
如图,一目标在A 区,到公路、铁路距离相等,离公路与铁路交叉处500 m,在图上标出它的位置(比例尺1:20 000).
如图,设公路、铁路的交点为O. 在A 区内作角的平分线OB,在OB上截取OC=2.5 cm,则点C即为所求.
解:
典题精讲
2
如图,在CD上求一点P,使它到边OA,OB 的距离相等,则点P 是( )
A.线段CD 的中点
B.CD 与过点O 作CD 的垂线的交点
C.CD 与∠AOB 的平分线的交点
D.以上均不对
C
典题精讲
3
如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD 与BC 相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法确定
A
典题精讲
4
如图,在△ABC 中,与∠ABC,∠ACB 相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF 平分BC
B.AF 平分∠BAC
C.AF⊥BC
D.以上结论都正确
B
易错提醒
如图,在△ABC 中,BD 平分∠ABC,交AC 于点D,BC 边上有一点E,连接DE,则AD 与DE 的数量关系为( )
A.AD>DE
B.AD=DE
C.ADD.不确定
易错点:运用角的平分线的性质时,常因忽略“到角两边的距离”而导致错误
D
学以致用
小试牛刀
1
如图,AB∥CD,BP 和CP 分别平分∠ABC 和∠DCB,AD 过点P,且与AB 垂直.若AD=8,则点P 到BC 的距离是( )
A.8
B.6
C.4
D.2
C
小试牛刀
2
如图,在Rt△ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点M,N,再分别以点M,N 为圆心,大于 MN 的长为半径画弧,两弧交于点P,作射线AP交边BC 于点D,若CD=4,AB=15,则△ABD 的面积是( )
A.15 B.30
C.45 D.60
B
小试牛刀
3
如图,在△ABC 中,AB=AC,D 为BC上一点,连接AD,E 为AD 上一点,EM⊥AB 于点M,EN⊥AC 于点N,则下面四个结论:①若AD⊥BC,则EM=EN;②若EM=EN,则∠BAD=∠CAD;③若EM=EN,则AM=AN;④若EM=EN,则∠AEM=∠AEN. 其中正确的有( )
A.1个 B.2个
C.3个 D.4个
D
小试牛刀
4 如图,AD 平分∠BAC,且BD=CD,DE⊥AB 于点E,DF⊥AC 于点F.
(1)求证:AB=AC;
(2)若AD=2 ,∠DAC=30°,求AC 的长.
小试牛刀
∵AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
又∵BD=CD,
∴Rt△BDE ≌ Rt△CDF (HL).
∴∠B=∠C.
∴AB=AC.
(1)证明:
小试牛刀
∵AB=AC,BD=CD,
∴AD⊥BC.
在Rt△ADC 中,∵∠DAC=30°,
∴DC= AC.
由AD 2+DC 2=AC 2,得(2 )2+ AC 2=AC 2,∴AC=4.
(2)解:
小试牛刀
5 如图,DE⊥AB 交AB 的延长线于E,DF⊥AC 于F,若BD=CD,BE=CF.
(1)求证:AD 平分∠BAC;
(2)直接写出AB+AC 与AE 之间的等量关系.
小试牛刀
在Rt△BDE 和Rt△CDF 中,
BD=CD,
BE=CF,
∴Rt△BDE ≌ Rt△CDF (HL).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴D 在∠BAC 的平分线上.
∴AD 平分∠BAC.
AB+AC=2AE.
(1)证明:
(2)解:
小试牛刀
6 (1)如图①,在Rt△ABC 中,∠C=90°,∠B=45°,AD 是△ABC 的角平分线,过点D 作DE⊥AB 于点E,则可以得到AC,CD,AB三条线段之间的数量关系为_________________.
(2)若将(1)中的条件“在Rt△ABC 中,∠C=90°,∠B=45°”改为“在△ABC 中,∠C=2∠B ”,如图②所示,则(1)中的结论是否仍然成立?证明你的猜想.
AB=AC+CD
小试牛刀
(2)(1)中的结论仍然成立.
证明如下:∵AD 是∠CAB 的平分线,
∴将△CAD 沿AD 折叠,点C 恰好落在AB 边上(设为点C ′).
∴△ACD ≌ △AC′D.
∴AC=AC ′,CD=C′D,
∠AC′D=∠C=2∠B.
又∵∠AC′D=∠C′DB+∠B,
∴∠C′DB=∠B.
∴C′D=C′B.
∴AB=AC ′+C′B=AC+C′D,即AB=AC+CD.
解:
小试牛刀
7 如图,在四边形ABDC 中,∠D=∠B=90°,O 为BD 的中点,且AO 平分∠BAC. 求证:
(1)CO 平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
小试牛刀
(1)如图,过点O 作OE⊥AC 于点E,
∵∠B=90°,AO 平分∠BAC,
∴OB=OE.
∵点O 为BD 的中点,
∴OB=OD.
∴OE=OD.
又∵∠D=90°,∠OEC=90°,
∴CO 平分∠ACD.
证明:
小试牛刀
(2)在Rt△ABO 和Rt△AEO 中,
AO=AO,
OE=OB,
∴Rt△ABO ≌ Rt△AEO (HL).
∴∠AOB=∠AOE= ∠BOE.
同理,∠COD=∠COE= ∠DOE.
∵∠AOC=∠AOE+∠COE,
∴∠AOC= ∠BOE+ ∠DOE= ×180°=90°.
∴OA⊥OC.
小试牛刀
(3)∵Rt△ABO ≌ Rt△AEO,
∴AB=AE.
同理可得CD=CE.
∵AC=AE+CE,
∴AB+CD=AC.
课堂小结
课堂小结
角的平分线的性质与判定定理的关系:
(1)都与距离有关,即垂直的条件都应具备.
(2)点在角的平分线上 点到这个角两边的距离相等.
(3)性质反映只要是角的平分线上的点,到角两边的距
离就一定相等;判定定理反映只要是到角两边距离
相等的点,都应在角的平分线上.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.角平分线
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
不利用工具,请你将一张用纸片做的角分成两个相等的角. 你有什么办法?
A
O
B
C
再打开纸片 ,看看折痕与这个角有何关系?
对折
新课精讲
探索新知
1
知识点
角平分线的性质
还记得角平分线上的点有什么性质吗?你是怎样得到的?请你尝试证明这性质,并与同伴交流.
A
B
O
P
C
D
E
探索新知
如图,任意作一个角∠AOB,作出 ∠AOB 的平分
线OC. 在OC上任取一点P,过点P 画出OA,OB 的垂
线,分别记垂足为D,E,测量 PD,PE 并作比较,你
得到什么结论?在OC 上再取
几个点试一试.
通过以上测量,你发现了
角的平分线的什么性质?
探索新知
1.性质:角的平分线上的点到角的两边的距离相等.
2.书写格式:
如图,∵OP 平分∠AOB,
PD⊥OA 于点D,PE⊥OB 于点E,∴PD=PE.
探索新知
B
A
D
O
P
E
C
定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
定理的作用:
证明线段相等.
探索新知
归 纳
定理 角平分线上的点到这个角的两边的距离相等.
探索新知
已知:如图,OC 是∠AOB 的平分线,点P 在OC上,PD丄OA,PE丄OB,垂足分别为D,E.
求证:PD=PE.
例1
O
D
A
C
E
P
1
2
探索新知
∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠PDO=∠PEO=90°.
∵∠1=∠2,OP=OP
∴△PDO ≌ △PEO ( AAS ).
∴PD=PE (全等三角形的对应边相等).
证明:
探索新知
例2
如图,在△ABC 中,∠BAC=60°,点D 在BC 上, AD=10,DE 丄AB, DF丄AC ,垂足分别为E,F,DE=DF,求DE 的长.
A
B
C
E
F
D
探索新知
解:
∵DE丄AB,DF丄AC,垂足分分别为E,F,
且DE=DF,
∴AD 平分∠BAC (在一个角的内部,到角的两边
距离相等的点在这个角的平分线上).
又∵∠BAC=60°,
∴∠BAD=30°.
在 Rt△ADE 中,∠AED=90°,AD=10,
∴DE= AD= ×10=5 (在直角三角形中,如果一个锐角等于30°. 那么它所对的直角边等于斜边的一半).
典题精讲
1
如图,AD,AE 分别是△ABC 中∠A 的内角平分线和外角平分线,它们有什么关系?
解:AD⊥AE.
C
D
B
A
E
F
典题精讲
2
如图,OP 是∠AOB 的平分线,点C,D 分别在角的两边OA,OB 上,添加下列条件,不能判定△POC ≌ △POD 的选项是( )
A.PC⊥OA,PD⊥OB
B.OC=OD
C.∠OPC=∠OPD
D.PC=PD
D
典题精讲
如图,OP 平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO 平分∠APB
C.OA=OB
D.AB 垂直平分OP
D
典题精讲
4
如图,点P 是∠AOB 平分线OC 上一点,PD⊥OB,垂足为D,若PD=2,则点P 到边OA 的距离是( )
A.2
B.3
C.
D.4
A
典题精讲
5
如图,在△ABC 中,∠C=90°,AC=BC,AD 平分∠CAB 交BC 于D,DE⊥AB 于E,若AB=6 cm,则△DBE 的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
探索新知
2
知识点
角平分线的判定
角平分线的性质:角的平分线上的点到角的两边的距离相等.
O
D
E
P
P 到OA 的距离
P 到OB 的距离
角平分线上的点
A
C
B
探索新知
如图,由 于点 D ,
于点E,PD = PE ,可
以得到什么结论 ?
OB
PE
⊥
PD
⊥
OA
B
A
D
O
P
E
到一个角的两边的距离相等的点, 在这个角的平分线上.
探索新知
证明过程:
已知:如图,点P 为∠AOB 内一点,PD丄OA,PE丄OB,垂足分别为D,E,且PD=PE.
求证:OP 平分∠AOB.
O
D
A
C
E
P
1
2
B
探索新知
∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠ODP=∠OEP=90°,
∵PD=PE,OP=OP,
∴Rt△DOP ≌ Rt△EOP ( HL ).
∴∠1=∠2 (全等三角形的对应角相等).
∴OP 平分∠AOB.
证明:
探索新知
判定方法:角的内部到角的两边的距离相等的点在角
的平分线上.
书写格式:如图,∵PD⊥OA,PE⊥OB,PD=PE, ∴点P 在∠AOB 的平分线上(或∠AOC=∠BOC ).
探索新知
如图,已知BE=CF,DF⊥AC 于点F,DE⊥AB 于点E,BF 和CE 相交于点D.
求证:AD 平分∠BAC.
例3
导引:
要证AD 平分∠BAC,已知条件
中有两个垂直,即有点到角的
两边的距离,再证这两个距离
相等即可证明结论,证这两条
垂线段相等,可通过证明
△BDE 和△CDF 全等来完成.
探索新知
∵DF⊥AC 于点F,DE⊥AB 于点E,
∴∠DEB=∠DFC=90°.
在△BDE 和△CDF 中,
∴△BDE ≌ △CDF (AAS).
∴DE=DF.
又∵DF⊥AC 于点F,DE⊥AB 于点E,
∴AD 平分∠BAC.
证明:
探索新知
总 结
判定角平分线有两步:
(1)找出与角的两边都垂直的垂线段;
(2)证明两条垂线段相等.
典题精讲
1
如图,一目标在A 区,到公路、铁路距离相等,离公路与铁路交叉处500 m,在图上标出它的位置(比例尺1:20 000).
如图,设公路、铁路的交点为O. 在A 区内作角的平分线OB,在OB上截取OC=2.5 cm,则点C即为所求.
解:
典题精讲
2
如图,在CD上求一点P,使它到边OA,OB 的距离相等,则点P 是( )
A.线段CD 的中点
B.CD 与过点O 作CD 的垂线的交点
C.CD 与∠AOB 的平分线的交点
D.以上均不对
C
典题精讲
3
如图,AD⊥OB,BC⊥OA,垂足分别为D,C,AD 与BC 相交于点P,若PA=PB,则∠1与∠2的大小关系是( )
A.∠1=∠2
B.∠1>∠2
C.∠1<∠2
D.无法确定
A
典题精讲
4
如图,在△ABC 中,与∠ABC,∠ACB 相邻的外角的平分线相交于点F,连接AF,则下列结论正确的是( )
A.AF 平分BC
B.AF 平分∠BAC
C.AF⊥BC
D.以上结论都正确
B
易错提醒
如图,在△ABC 中,BD 平分∠ABC,交AC 于点D,BC 边上有一点E,连接DE,则AD 与DE 的数量关系为( )
A.AD>DE
B.AD=DE
C.AD
易错点:运用角的平分线的性质时,常因忽略“到角两边的距离”而导致错误
D
学以致用
小试牛刀
1
如图,AB∥CD,BP 和CP 分别平分∠ABC 和∠DCB,AD 过点P,且与AB 垂直.若AD=8,则点P 到BC 的距离是( )
A.8
B.6
C.4
D.2
C
小试牛刀
2
如图,在Rt△ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点M,N,再分别以点M,N 为圆心,大于 MN 的长为半径画弧,两弧交于点P,作射线AP交边BC 于点D,若CD=4,AB=15,则△ABD 的面积是( )
A.15 B.30
C.45 D.60
B
小试牛刀
3
如图,在△ABC 中,AB=AC,D 为BC上一点,连接AD,E 为AD 上一点,EM⊥AB 于点M,EN⊥AC 于点N,则下面四个结论:①若AD⊥BC,则EM=EN;②若EM=EN,则∠BAD=∠CAD;③若EM=EN,则AM=AN;④若EM=EN,则∠AEM=∠AEN. 其中正确的有( )
A.1个 B.2个
C.3个 D.4个
D
小试牛刀
4 如图,AD 平分∠BAC,且BD=CD,DE⊥AB 于点E,DF⊥AC 于点F.
(1)求证:AB=AC;
(2)若AD=2 ,∠DAC=30°,求AC 的长.
小试牛刀
∵AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
又∵BD=CD,
∴Rt△BDE ≌ Rt△CDF (HL).
∴∠B=∠C.
∴AB=AC.
(1)证明:
小试牛刀
∵AB=AC,BD=CD,
∴AD⊥BC.
在Rt△ADC 中,∵∠DAC=30°,
∴DC= AC.
由AD 2+DC 2=AC 2,得(2 )2+ AC 2=AC 2,∴AC=4.
(2)解:
小试牛刀
5 如图,DE⊥AB 交AB 的延长线于E,DF⊥AC 于F,若BD=CD,BE=CF.
(1)求证:AD 平分∠BAC;
(2)直接写出AB+AC 与AE 之间的等量关系.
小试牛刀
在Rt△BDE 和Rt△CDF 中,
BD=CD,
BE=CF,
∴Rt△BDE ≌ Rt△CDF (HL).
∴DE=DF.
又∵DE⊥AB,DF⊥AC,
∴D 在∠BAC 的平分线上.
∴AD 平分∠BAC.
AB+AC=2AE.
(1)证明:
(2)解:
小试牛刀
6 (1)如图①,在Rt△ABC 中,∠C=90°,∠B=45°,AD 是△ABC 的角平分线,过点D 作DE⊥AB 于点E,则可以得到AC,CD,AB三条线段之间的数量关系为_________________.
(2)若将(1)中的条件“在Rt△ABC 中,∠C=90°,∠B=45°”改为“在△ABC 中,∠C=2∠B ”,如图②所示,则(1)中的结论是否仍然成立?证明你的猜想.
AB=AC+CD
小试牛刀
(2)(1)中的结论仍然成立.
证明如下:∵AD 是∠CAB 的平分线,
∴将△CAD 沿AD 折叠,点C 恰好落在AB 边上(设为点C ′).
∴△ACD ≌ △AC′D.
∴AC=AC ′,CD=C′D,
∠AC′D=∠C=2∠B.
又∵∠AC′D=∠C′DB+∠B,
∴∠C′DB=∠B.
∴C′D=C′B.
∴AB=AC ′+C′B=AC+C′D,即AB=AC+CD.
解:
小试牛刀
7 如图,在四边形ABDC 中,∠D=∠B=90°,O 为BD 的中点,且AO 平分∠BAC. 求证:
(1)CO 平分∠ACD;
(2)OA⊥OC;
(3)AB+CD=AC.
小试牛刀
(1)如图,过点O 作OE⊥AC 于点E,
∵∠B=90°,AO 平分∠BAC,
∴OB=OE.
∵点O 为BD 的中点,
∴OB=OD.
∴OE=OD.
又∵∠D=90°,∠OEC=90°,
∴CO 平分∠ACD.
证明:
小试牛刀
(2)在Rt△ABO 和Rt△AEO 中,
AO=AO,
OE=OB,
∴Rt△ABO ≌ Rt△AEO (HL).
∴∠AOB=∠AOE= ∠BOE.
同理,∠COD=∠COE= ∠DOE.
∵∠AOC=∠AOE+∠COE,
∴∠AOC= ∠BOE+ ∠DOE= ×180°=90°.
∴OA⊥OC.
小试牛刀
(3)∵Rt△ABO ≌ Rt△AEO,
∴AB=AE.
同理可得CD=CE.
∵AC=AE+CE,
∴AB+CD=AC.
课堂小结
课堂小结
角的平分线的性质与判定定理的关系:
(1)都与距离有关,即垂直的条件都应具备.
(2)点在角的平分线上 点到这个角两边的距离相等.
(3)性质反映只要是角的平分线上的点,到角两边的距
离就一定相等;判定定理反映只要是到角两边距离
相等的点,都应在角的平分线上.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
