【班海精品】北师大版(新)八年级下-1.4角平分线 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-1.4角平分线 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 15:34:56 | ||
图片预览










文档简介
(共35张PPT)
4.角平分线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
角平分线的性质与判定的内容是什么?
复
习
回
顾
情景导入
归 纳
定理 角平分线上的点到这个角的两边的距离相等.
定理 在一个角的内部,到角的两边距离相等的点
在这个角的平分线上.
新课精讲
探索新知
1
知识点
三角形的角平分线
求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
例1
探索新知
已知:如图,在△ABC 中,角平分线BM 与角平分线CN 相交于点P,过点P 分别作AB,BC,AC,的垂线,垂足分别为D,E,F.
求证:∠A 的平分线经过点P,且PD=PE=PF.
探索新知
∵BM 是△ABC 的角平分线,点P 在BM上,且PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P 在∠A 的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),即∠A 的平分线经过点P.
证明:
探索新知
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等.
探索新知
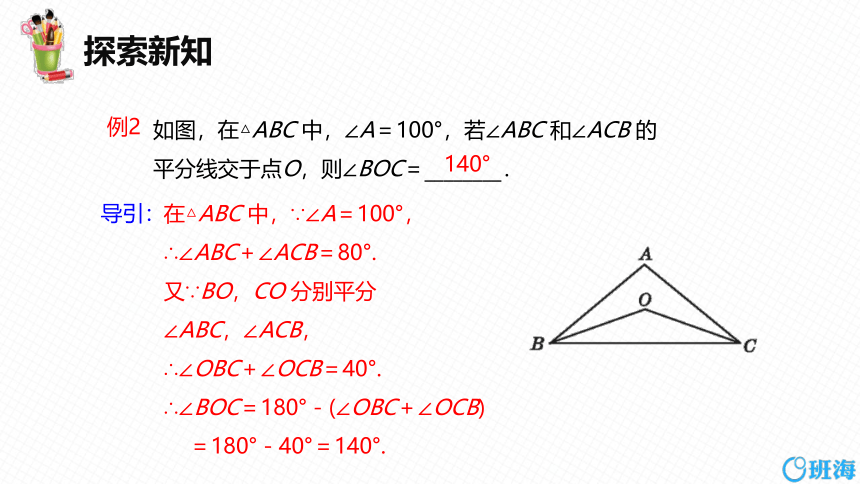
如图,在△ABC 中,∠A=100°,若∠ABC 和∠ACB 的平分线交于点O,则∠BOC=________.
例2
导引:
在△ABC 中,∵∠A=100°,
∴∠ABC+∠ACB=80°.
又∵BO,CO 分别平分
∠ABC,∠ACB,
∴∠OBC+∠OCB=40°.
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-40°=140°.
140°
探索新知
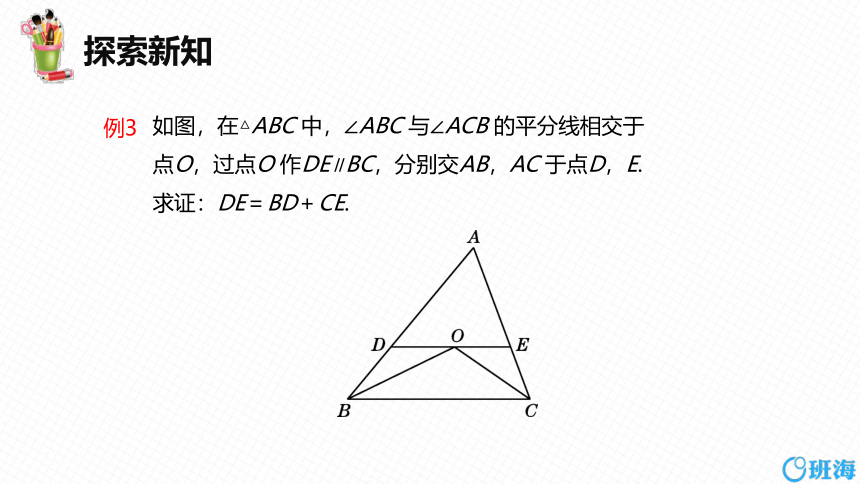
如图,在△ABC 中,∠ABC 与∠ACB 的平分线相交于点O,过点O 作DE∥BC,分别交AB,AC 于点D,E.
求证:DE=BD+CE.
例3
探索新知
证明:
∵BO 平分∠ABC,
∴∠ABO=∠CBO.
∵DE∥BC,∴∠CBO=∠DOB.
∴∠ABO=∠DOB. ∴BD=OD.
同理可证OE=CE,
∴DE=OD+OE=BD+CE.
探索新知
角平分线和平行线都可以得出角相等,由角相等可以得出线段相等,进而可以进行线段之间的转化,达到证明线段之间和差倍分关系的目的.
总 结
典题精讲
1
已知:如图,在Rt△ABC 中,∠ACB=90°, ∠B=60°,AD,CE 是角平分线,AD与CE 相交于点F,FM⊥AB,FN⊥BC,垂足分别为 M,N. 求证:FE=FD.
连接BF,由题意易知BF 即
为∠ABC 的平分线,则FM=FN,
在Rt△ABC 中,∵∠B=60°,
∴∠BAC=30°. ∴∠DAB= ∠BAC=15°.
解:
典题精讲
∴∠FDN=∠DAB+∠B=75°,
∠FEM=∠BAC+∠ACE
=30°+ ∠ACB=30°+45°=75°.
∴∠FEM=∠FDN.
在△FEM 与△FDN 中,
∴△FEM ≌ △FDN.
∴FE=FD.
典题精讲
2
在△ABC 内到三条边距离相等的点是△ABC 的( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.以上均不对
B
3
到三角形三边距离相等的点的个数是( )
A.1 B.2
C.3 D.4
D
探索新知
2
知识点
角平分线性质的应用
角平分线的性质是证明边相等的重要依据,常与直角三角形的性质、勾股定理其逆定理等综合应用,在应用中常用到“构造法”和“转化思想”.
探索新知
如图,在△ABC 中,AC=BC,∠C=90°,AD 是△ABC 的角平分线,DE丄AB 垂足为E,
(1) 已知CD=4 cm,求AC 的长;
(2) 求证:AB=AC+CD.
例4
A
B
C
D
E
探索新知
∵AD 是△ABC 的角平分线,DC丄AC,DE丄AB 垂足为E,
∴ DE=CD=4 cm (角平分线上的点到这个角的两边的距离相等).
∵AC=BC,∴ ∠B=∠BAC, (等边对等角).
∵ ∠C=90°,
∴∠BDE=90°-45°=45° .
∴ BE=DE (等角对等边).
在等腰直角三角形BDE 中,
∴ AC=BC=CD+BD=
(1) 解:
探索新知
由(1)的求解过程易知,
Rt △ACD ≌ Rt△AED (HL).
∴ AC=AE (全等三角形的对应边相等)
∵ BE=DE=CD,
∴ AB=AE+BE=AC+CD.
(2) 证明:
典题精讲
已知△ABC,求作一点P,使P 到∠A 的两边的距离相等,且PA=PB.下列确定P 点的方法正确的是( )
A.P 为∠A 与∠B 的平分线的交点
B.P 为∠A 的平分线与AB 的垂直平分线的交点
C.P 为AC,AB 两边上的高的交点
D.P 为AC,AB 两边的垂直平分线的交点
B
典题精讲
2 如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:(1)使其到两公路的距离相等;(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
如图,连接EF,作∠ACB 的平分线交EF 于点O,则点O就是所要建超市的位置.
解:
学以致用
小试牛刀
如图,在△ABC 中,∠ABC,∠ACB 的平分线相交于点O,
下面结论正确的是( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.不能确定
B
小试牛刀
2 如图,△ABC 的三边AB,BC,CA 的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶S△CAO=____________.
4:5:6
小试牛刀
3 如图,某公园角落里有一块三角形的绿草地,工作人员想在草地上安装一个自动喷水头进行浇灌.现有两种方案:
小试牛刀
(1)作∠A,∠B 的平分线,交点为P,建在点P 处;
(2)作AB,AC 的垂直平分线,交点为Q,建在点Q 处.
请你在如图①②所示的两幅图中分别作出点P,Q,结合实际情况,说明哪种方案更合理.
小试牛刀
如图①②.
方案(2)更合理.要使三角形的绿草地都能被浇到水,水就必须要洒到三角形的各个顶点处,所以自动喷水头必须安装在三角形的三边垂直平分线的交点处.
解:
小试牛刀
4 如图,OE,OF 分别是△ABC 中AB,AC 边的中垂线(即垂直平分线),∠OBC,∠OCB 的平分线相交于点I,试判断OI 与BC 的位置关系,并给出证明.
小试牛刀
OI⊥BC.
证明:如图,连接AO,延长OI 交BC 于点M.
∵OE,OF 分别为AB,AC 的中垂线,
∴OA=OB,OA=OC.
∴OB=OC.
又∵BI,CI 分别为∠OBC,∠OCB 的平分线,
∴点I 必在∠BOC 的平分线上.
∴∠BOI=∠COI.
解:
小试牛刀
在△BOM 和△COM 中,
OB=OC,
∠BOM=∠COM,
OM=OM,
∴△BOM ≌ △COM (SAS).
∴∠BMO=∠CMO.
又∵∠BMO+∠CMO=180°,
∴∠BMO=∠CMO=90°.
即OI ⊥BC.
课堂小结
课堂小结
三角形三条内角平分线的交点到三边的距离相等是三角形的一个重要特征,该交点与三角形三个顶点的连线形成三个等高的小三角形,利用三个小三角形的面积之和等于原三角形的面积,求角平分线交点到三边距离或者求三角形的面积,体现等面积法的运用.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.角平分线
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
角平分线的性质与判定的内容是什么?
复
习
回
顾
情景导入
归 纳
定理 角平分线上的点到这个角的两边的距离相等.
定理 在一个角的内部,到角的两边距离相等的点
在这个角的平分线上.
新课精讲
探索新知
1
知识点
三角形的角平分线
求证:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.
例1
探索新知
已知:如图,在△ABC 中,角平分线BM 与角平分线CN 相交于点P,过点P 分别作AB,BC,AC,的垂线,垂足分别为D,E,F.
求证:∠A 的平分线经过点P,且PD=PE=PF.
探索新知
∵BM 是△ABC 的角平分线,点P 在BM上,且PD丄AB,PE丄BC,垂足分别为D,E,
∴PD=PE (角平分线上的点到这个角的两边的距离相等).
同理,PE=PF.
∴PD=PE=PF.
∴点P 在∠A 的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上),即∠A 的平分线经过点P.
证明:
探索新知
三角形的三条角平分线相交于一点,并且这一点到三角形三条边的距离相等.
探索新知
如图,在△ABC 中,∠A=100°,若∠ABC 和∠ACB 的平分线交于点O,则∠BOC=________.
例2
导引:
在△ABC 中,∵∠A=100°,
∴∠ABC+∠ACB=80°.
又∵BO,CO 分别平分
∠ABC,∠ACB,
∴∠OBC+∠OCB=40°.
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-40°=140°.
140°
探索新知
如图,在△ABC 中,∠ABC 与∠ACB 的平分线相交于点O,过点O 作DE∥BC,分别交AB,AC 于点D,E.
求证:DE=BD+CE.
例3
探索新知
证明:
∵BO 平分∠ABC,
∴∠ABO=∠CBO.
∵DE∥BC,∴∠CBO=∠DOB.
∴∠ABO=∠DOB. ∴BD=OD.
同理可证OE=CE,
∴DE=OD+OE=BD+CE.
探索新知
角平分线和平行线都可以得出角相等,由角相等可以得出线段相等,进而可以进行线段之间的转化,达到证明线段之间和差倍分关系的目的.
总 结
典题精讲
1
已知:如图,在Rt△ABC 中,∠ACB=90°, ∠B=60°,AD,CE 是角平分线,AD与CE 相交于点F,FM⊥AB,FN⊥BC,垂足分别为 M,N. 求证:FE=FD.
连接BF,由题意易知BF 即
为∠ABC 的平分线,则FM=FN,
在Rt△ABC 中,∵∠B=60°,
∴∠BAC=30°. ∴∠DAB= ∠BAC=15°.
解:
典题精讲
∴∠FDN=∠DAB+∠B=75°,
∠FEM=∠BAC+∠ACE
=30°+ ∠ACB=30°+45°=75°.
∴∠FEM=∠FDN.
在△FEM 与△FDN 中,
∴△FEM ≌ △FDN.
∴FE=FD.
典题精讲
2
在△ABC 内到三条边距离相等的点是△ABC 的( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.以上均不对
B
3
到三角形三边距离相等的点的个数是( )
A.1 B.2
C.3 D.4
D
探索新知
2
知识点
角平分线性质的应用
角平分线的性质是证明边相等的重要依据,常与直角三角形的性质、勾股定理其逆定理等综合应用,在应用中常用到“构造法”和“转化思想”.
探索新知
如图,在△ABC 中,AC=BC,∠C=90°,AD 是△ABC 的角平分线,DE丄AB 垂足为E,
(1) 已知CD=4 cm,求AC 的长;
(2) 求证:AB=AC+CD.
例4
A
B
C
D
E
探索新知
∵AD 是△ABC 的角平分线,DC丄AC,DE丄AB 垂足为E,
∴ DE=CD=4 cm (角平分线上的点到这个角的两边的距离相等).
∵AC=BC,∴ ∠B=∠BAC, (等边对等角).
∵ ∠C=90°,
∴∠BDE=90°-45°=45° .
∴ BE=DE (等角对等边).
在等腰直角三角形BDE 中,
∴ AC=BC=CD+BD=
(1) 解:
探索新知
由(1)的求解过程易知,
Rt △ACD ≌ Rt△AED (HL).
∴ AC=AE (全等三角形的对应边相等)
∵ BE=DE=CD,
∴ AB=AE+BE=AC+CD.
(2) 证明:
典题精讲
已知△ABC,求作一点P,使P 到∠A 的两边的距离相等,且PA=PB.下列确定P 点的方法正确的是( )
A.P 为∠A 与∠B 的平分线的交点
B.P 为∠A 的平分线与AB 的垂直平分线的交点
C.P 为AC,AB 两边上的高的交点
D.P 为AC,AB 两边的垂直平分线的交点
B
典题精讲
2 如图,李明计划在张村、李村之间建一家超市.张、李两村坐落在两相交公路内.超市的位置应满足下列条件:(1)使其到两公路的距离相等;(2)为了方便群众,超市到两村的距离之和最短,请你通过作图确定要建超市的位置.
如图,连接EF,作∠ACB 的平分线交EF 于点O,则点O就是所要建超市的位置.
解:
学以致用
小试牛刀
如图,在△ABC 中,∠ABC,∠ACB 的平分线相交于点O,
下面结论正确的是( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.不能确定
B
小试牛刀
2 如图,△ABC 的三边AB,BC,CA 的长分别为40,50,60,其三条角平分线交于点O,则S△ABO∶S△BCO∶S△CAO=____________.
4:5:6
小试牛刀
3 如图,某公园角落里有一块三角形的绿草地,工作人员想在草地上安装一个自动喷水头进行浇灌.现有两种方案:
小试牛刀
(1)作∠A,∠B 的平分线,交点为P,建在点P 处;
(2)作AB,AC 的垂直平分线,交点为Q,建在点Q 处.
请你在如图①②所示的两幅图中分别作出点P,Q,结合实际情况,说明哪种方案更合理.
小试牛刀
如图①②.
方案(2)更合理.要使三角形的绿草地都能被浇到水,水就必须要洒到三角形的各个顶点处,所以自动喷水头必须安装在三角形的三边垂直平分线的交点处.
解:
小试牛刀
4 如图,OE,OF 分别是△ABC 中AB,AC 边的中垂线(即垂直平分线),∠OBC,∠OCB 的平分线相交于点I,试判断OI 与BC 的位置关系,并给出证明.
小试牛刀
OI⊥BC.
证明:如图,连接AO,延长OI 交BC 于点M.
∵OE,OF 分别为AB,AC 的中垂线,
∴OA=OB,OA=OC.
∴OB=OC.
又∵BI,CI 分别为∠OBC,∠OCB 的平分线,
∴点I 必在∠BOC 的平分线上.
∴∠BOI=∠COI.
解:
小试牛刀
在△BOM 和△COM 中,
OB=OC,
∠BOM=∠COM,
OM=OM,
∴△BOM ≌ △COM (SAS).
∴∠BMO=∠CMO.
又∵∠BMO+∠CMO=180°,
∴∠BMO=∠CMO=90°.
即OI ⊥BC.
课堂小结
课堂小结
三角形三条内角平分线的交点到三边的距离相等是三角形的一个重要特征,该交点与三角形三个顶点的连线形成三个等高的小三角形,利用三个小三角形的面积之和等于原三角形的面积,求角平分线交点到三边距离或者求三角形的面积,体现等面积法的运用.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
