【班海精品】北师大版(新)八年级下-1.2直角三角形 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-1.2直角三角形 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览











文档简介
(共47张PPT)
2.直角三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. 你能帮工作人员想个办法吗?
新课精讲
探索新知
1
知识点
判定两直角三角形全等的方法:斜边、直角边
问题 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C ′,使∠C ′=90°,B′C ′=BC,A′B ′=AB,然后把画好的Rt△A′B′C ′剪下来放到Rt△ABC 上,你发现了什么?
探索新知
A
B
C
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C ′=BC;
(3)以B ′为圆心,AB 为半径画弧,
交射线C′ N 于点A′;
(4)连接A′B ′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A′
N
M
C′
B′
探索新知
由上面可以得到判定两个直角三角形全等的一个方法:
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、 直角边”或“HL”).
归 纳
探索新知
定理 斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在 △ABC 与△A′B′C′ 中,∠C=∠C′=90°,AB=A′B′,
求证: △ABC ≌ △A′B′C′
A
B
C
A’
B’
C’
探索新知
在△ABC 中,
∵∠C= 90°,
∴BC 2= AB 2-AC 2 (勾股定理).
同理, B′C′ 2=A′B′ 2-A′C′ 2.
∵AB=A′B′, AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′ (SSS).
证明:
探索新知
1.斜边和一条直角边分别相等的两个直角三角形全等(简
写成“斜边、直角边”或“HL”).
2.(1)书写格式:如图,在Rt△ABC 和Rt△A′B ′C ′中,
∴Rt△ABC ≌ Rt△A′B ′C ′.
(2)注意点:书写时必须强调直
角三角形.
探索新知
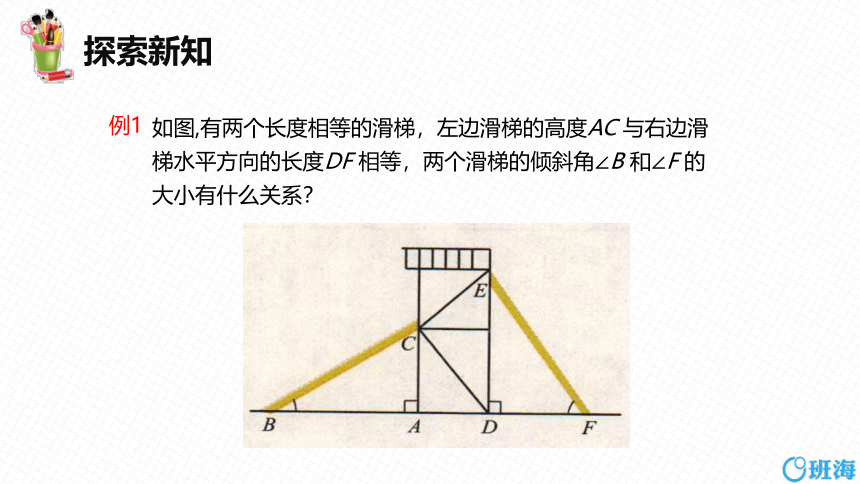
如图,有两个长度相等的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠B 和∠F 的大小有什么关系?
例1
探索新知
根据题意,可知
∠BAC=∠EDF=90°,BC=EF,AC=DF,
∴Rt△BAC ≌ Rt△EDF (HL).
∴∠B=∠DEF (全等三角形的对应角相等).
∵∠DEF+∠F=90°,(直角三角形的两锐角互余),
∴∠B+∠F=90°
解:
探索新知
如图,在△ABC 中,AB=CB,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.
求证: Rt△ABE ≌ Rt△CBF.
导引:
根据AB=CB,∠ABE=
∠CBF=90°,AE=CF,
可利用“HL”证明
Rt△ABE ≌ Rt△CBF.
例2
探索新知
证明:
∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE 和Rt△CBF 中,
∵AE=CF,AB=CB,
∴Rt△ABE ≌ Rt△CBF (HL).
探索新知
应用“HL”判定两个直角三角形全等,书写时,
两个三角形符号前要加上“Rt”.
总 结
典题精讲
1
如图,两根长度均为12 m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木粧上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
两个木桩离旗杆底部的距离相等.
理由如下:在Rt△ABO 和Rt△ACO 中,
所以Rt△ABO ≌ Rt△ACO (HL).
所以BO=CO.
故两个木桩离旗杆底部的距离相等.
解:
典题精讲
2
如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD 全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
典题精讲
3
下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
典题精讲
4
如图,OD⊥AB 于D,OP⊥AC 于P,且OD=OP,则△AOD 与△AOP 全等的理由是( )
A.SSS
B.ASA
C.SSA
D.HL
D
探索新知
2
知识点
直角三角形全等的综合判定
直角三角形全等的判定既可以用“SSS” “SAS” “ASA”和“AAS”, 有可以用 “HL”.
探索新知
如图,已知∠B=∠C,添加一个条件使△ABD ≌ △ACE (不标注新的字母,不添加新的线段),你添加的条件是_________________________________
_________________________.
导引:
本题给出∠B=∠C,再加上公共角
∠A,有两个条件满足全等,根据全
等三角形的判定方法,有两个角全等
的判定方法有AAS,ASA,只要添加
其中任意一个角的对边相等即可,即AB=AC 或AD=
AE 或BD=CE;如果从已知给定的全等条件中,通过添
加另外一个条件能够得到AB=AC 或AD=AE 或BD=CE 中任意一个条件也可以,即BE=CD.
例3
AB=AC 或AD=AE 或BD=CE 或
BE=CD (写出一个即可)
探索新知
证明两个三角形全等,一般情况下是已知两个条件去找第三个全等条件,有以下几种情况:
总 结
(4)已知一边及其对角,只能找任意一角.
典题精讲
1
判断下列命题的真假,并说明理由:
(1)两个锐角分别相等的两个直角三角形全等;
(2)两条直角边分别相等的两个直角三角形全等;
(3)一条直角边相等且另一条直角边上的中线相
等的两个直角三角形全等.
典题精讲
(1)假.理由:如图,
在Rt△ABC 和Rt△AB′C ′中,
∠A=∠A,∠AB′C ′=∠ABC,
但Rt△ABC 与Rt△AB′C ′不全等.
(2)真.理由:因为该命题满足“AAS”公理的条件.
(3)真.理由:因为该命题满足“SAS”公理的条件.
(4)真.先利用“HL”定理得到另一条直角边的一半
相等,也即该直角边相等,再根据“SAS”公理可
判定两个三角形全等.
解:
典题精讲
下列条件中,利用基本尺规作图,不能作出唯一直角三角形的是( )
A.已知斜边和一锐角
B.已知一锐角和它所对的直角边
C.已知斜边和一直角边
D.已知两个锐角
D
2
典题精讲
如图,在△ABC 中,AD⊥BC,D 为BC 的中点,以下结论:①△ABD ≌ △ACD;②AB=AC;③∠B=∠C;④AD 是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
3
典题精讲
如图,P,Q 分别是BC,AC上的点,过点P 作PR⊥AB 于R 点,作PS⊥AC 于S 点,若AQ=PQ,PR=PS,下面三个结论:①AS=AR;②QP∥AR;③△BRP ≌ △CSP. 正确的是( )
A.①③
B.②③
C.①②
D.①②③
C
4
易错提醒
如图,AD,BC 相交于点O,AD=BC,∠C=∠D=90°,
(1)求证:△ACB ≌ △BDA;
(2)若∠ABC=35°,
则∠CAO=________.
易错点:用“斜边、直角边”证明全等时不指出是直角三角形导致出错
20°
易错提醒
∵∠C=∠D=90°,
∴△ACB 和△BDA 都是直角三角形.
在Rt△ACB 和Rt△BDA 中,
BC=AD,
AB=BA,
∴Rt△ACB ≌ Rt△BDA.
(1)证明:
学以致用
小试牛刀
1
如图,在△ABC 中,∠C=90°,ED⊥AB 于点D,BD=BC,若AC=6 cm,则AE+DE 等于( )
A.4 cm
B.5 cm
C.6 cm
D.7 cm
C
小试牛刀
2
如图,在Rt△ABC 中,∠C=90°,∠B=30°,AB=4,则下列各图中的直角三角形与Rt△ABC 全等的是( )
A
小试牛刀
3 如图,在△ABC 中,AB=CB,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.
(1)求证:Rt△ABE ≌ Rt△CBF;
(2)若∠CAE=30°,求∠ACF 的度数.
小试牛刀
∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE 和Rt△CBF 中,
∵AE=CF,AB=CB,
∴Rt△ABE ≌ Rt△CBF (HL).
(1)证明:
小试牛刀
∵AB=CB,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∴∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE ≌ Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
(2)解:
小试牛刀
4 如图,在△ABC 中,∠ACB=90°,AC=BC,直线MN 经过点C,且AD⊥MN 于D,BE⊥MN 于E.
求证:DE=AD+BE.
小试牛刀
∵∠ACB=90°,∴∠ACD+∠BCE=90°.
又∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°.
∴∠ACD+∠DAC=90°.∴∠BCE=∠CAD.
在△ADC 和△CEB 中,
∵∠CAD=∠BCE,∠ADC=∠CEB,AC=CB,
∴△ADC ≌ △CEB (AAS).
∴AD=CE,DC=EB.
又∵DE=CE+DC,∴DE=AD+BE.
证明:
小试牛刀
5 如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.
求证:F 是CD 的中点.
小试牛刀
如图,连接AC,AD.在△ABC 和△AED 中,
AB=AE,
∠B=∠E,
BC=ED,
∴△ABC ≌ △AED (SAS).
∴AC=AD.
又∵AF⊥CD,
∴CF=DF.
即F 为CD 的中点.
证明:
小试牛刀
6 感知:如图①,AD 平分∠BAC. ∠B+∠C=180°,∠B=90°,易知DB=DC.
探究:如图②,AD 平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图③,在四边形ABDC 中,∠B=45°,∠C=135°,DB=DC=a,则AB-AC=________(用含a 的代数式表示)
小试牛刀
如图,过点D 作DE⊥AB 于E,
DF⊥AC 交AC 的延长线于F.
∵AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴∠DAC=∠DAB,∠F=∠AED=90°.
又∵AD=AD,
∴△AFD ≌ △AED.
∴DE=DF.
∵∠B+∠ACD=180°,
∠ACD+∠FCD=180°,
∴∠B=∠FCD.
证明:
小试牛刀
在△DFC 和△DEB 中,
∠F=∠DEB=90°,
∠FCD=∠B,
DF=DE,
∴△DFC ≌ △DEB.
∴DC=DB.
课堂小结
课堂小结
1.直角三角形的判定方法:
边边边、边角边、角边角、角角边、
斜边、直角边.
课堂小结
2. 判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,
用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边是锐
角的对边,用“AAS”判定;②直角边是锐角的邻边,
用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.直角三角形
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. 你能帮工作人员想个办法吗?
新课精讲
探索新知
1
知识点
判定两直角三角形全等的方法:斜边、直角边
问题 任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C ′,使∠C ′=90°,B′C ′=BC,A′B ′=AB,然后把画好的Rt△A′B′C ′剪下来放到Rt△ABC 上,你发现了什么?
探索新知
A
B
C
(1)画∠MC′N =90°;
(2)在射线C′M上取B′C ′=BC;
(3)以B ′为圆心,AB 为半径画弧,
交射线C′ N 于点A′;
(4)连接A′B ′.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A′
N
M
C′
B′
探索新知
由上面可以得到判定两个直角三角形全等的一个方法:
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、 直角边”或“HL”).
归 纳
探索新知
定理 斜边和一条直角边分别相等的两个直角三角形全等.
已知:如图,在 △ABC 与△A′B′C′ 中,∠C=∠C′=90°,AB=A′B′,
求证: △ABC ≌ △A′B′C′
A
B
C
A’
B’
C’
探索新知
在△ABC 中,
∵∠C= 90°,
∴BC 2= AB 2-AC 2 (勾股定理).
同理, B′C′ 2=A′B′ 2-A′C′ 2.
∵AB=A′B′, AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′ (SSS).
证明:
探索新知
1.斜边和一条直角边分别相等的两个直角三角形全等(简
写成“斜边、直角边”或“HL”).
2.(1)书写格式:如图,在Rt△ABC 和Rt△A′B ′C ′中,
∴Rt△ABC ≌ Rt△A′B ′C ′.
(2)注意点:书写时必须强调直
角三角形.
探索新知
如图,有两个长度相等的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等,两个滑梯的倾斜角∠B 和∠F 的大小有什么关系?
例1
探索新知
根据题意,可知
∠BAC=∠EDF=90°,BC=EF,AC=DF,
∴Rt△BAC ≌ Rt△EDF (HL).
∴∠B=∠DEF (全等三角形的对应角相等).
∵∠DEF+∠F=90°,(直角三角形的两锐角互余),
∴∠B+∠F=90°
解:
探索新知
如图,在△ABC 中,AB=CB,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.
求证: Rt△ABE ≌ Rt△CBF.
导引:
根据AB=CB,∠ABE=
∠CBF=90°,AE=CF,
可利用“HL”证明
Rt△ABE ≌ Rt△CBF.
例2
探索新知
证明:
∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE 和Rt△CBF 中,
∵AE=CF,AB=CB,
∴Rt△ABE ≌ Rt△CBF (HL).
探索新知
应用“HL”判定两个直角三角形全等,书写时,
两个三角形符号前要加上“Rt”.
总 结
典题精讲
1
如图,两根长度均为12 m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木粧上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.
两个木桩离旗杆底部的距离相等.
理由如下:在Rt△ABO 和Rt△ACO 中,
所以Rt△ABO ≌ Rt△ACO (HL).
所以BO=CO.
故两个木桩离旗杆底部的距离相等.
解:
典题精讲
2
如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD 全等.以下给出的条件适合的是( )
A.AC=AD
B.AB=AB
C.∠ABC=∠ABD
D.∠BAC=∠BAD
A
典题精讲
3
下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
典题精讲
4
如图,OD⊥AB 于D,OP⊥AC 于P,且OD=OP,则△AOD 与△AOP 全等的理由是( )
A.SSS
B.ASA
C.SSA
D.HL
D
探索新知
2
知识点
直角三角形全等的综合判定
直角三角形全等的判定既可以用“SSS” “SAS” “ASA”和“AAS”, 有可以用 “HL”.
探索新知
如图,已知∠B=∠C,添加一个条件使△ABD ≌ △ACE (不标注新的字母,不添加新的线段),你添加的条件是_________________________________
_________________________.
导引:
本题给出∠B=∠C,再加上公共角
∠A,有两个条件满足全等,根据全
等三角形的判定方法,有两个角全等
的判定方法有AAS,ASA,只要添加
其中任意一个角的对边相等即可,即AB=AC 或AD=
AE 或BD=CE;如果从已知给定的全等条件中,通过添
加另外一个条件能够得到AB=AC 或AD=AE 或BD=CE 中任意一个条件也可以,即BE=CD.
例3
AB=AC 或AD=AE 或BD=CE 或
BE=CD (写出一个即可)
探索新知
证明两个三角形全等,一般情况下是已知两个条件去找第三个全等条件,有以下几种情况:
总 结
(4)已知一边及其对角,只能找任意一角.
典题精讲
1
判断下列命题的真假,并说明理由:
(1)两个锐角分别相等的两个直角三角形全等;
(2)两条直角边分别相等的两个直角三角形全等;
(3)一条直角边相等且另一条直角边上的中线相
等的两个直角三角形全等.
典题精讲
(1)假.理由:如图,
在Rt△ABC 和Rt△AB′C ′中,
∠A=∠A,∠AB′C ′=∠ABC,
但Rt△ABC 与Rt△AB′C ′不全等.
(2)真.理由:因为该命题满足“AAS”公理的条件.
(3)真.理由:因为该命题满足“SAS”公理的条件.
(4)真.先利用“HL”定理得到另一条直角边的一半
相等,也即该直角边相等,再根据“SAS”公理可
判定两个三角形全等.
解:
典题精讲
下列条件中,利用基本尺规作图,不能作出唯一直角三角形的是( )
A.已知斜边和一锐角
B.已知一锐角和它所对的直角边
C.已知斜边和一直角边
D.已知两个锐角
D
2
典题精讲
如图,在△ABC 中,AD⊥BC,D 为BC 的中点,以下结论:①△ABD ≌ △ACD;②AB=AC;③∠B=∠C;④AD 是△ABC的角平分线.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
D
3
典题精讲
如图,P,Q 分别是BC,AC上的点,过点P 作PR⊥AB 于R 点,作PS⊥AC 于S 点,若AQ=PQ,PR=PS,下面三个结论:①AS=AR;②QP∥AR;③△BRP ≌ △CSP. 正确的是( )
A.①③
B.②③
C.①②
D.①②③
C
4
易错提醒
如图,AD,BC 相交于点O,AD=BC,∠C=∠D=90°,
(1)求证:△ACB ≌ △BDA;
(2)若∠ABC=35°,
则∠CAO=________.
易错点:用“斜边、直角边”证明全等时不指出是直角三角形导致出错
20°
易错提醒
∵∠C=∠D=90°,
∴△ACB 和△BDA 都是直角三角形.
在Rt△ACB 和Rt△BDA 中,
BC=AD,
AB=BA,
∴Rt△ACB ≌ Rt△BDA.
(1)证明:
学以致用
小试牛刀
1
如图,在△ABC 中,∠C=90°,ED⊥AB 于点D,BD=BC,若AC=6 cm,则AE+DE 等于( )
A.4 cm
B.5 cm
C.6 cm
D.7 cm
C
小试牛刀
2
如图,在Rt△ABC 中,∠C=90°,∠B=30°,AB=4,则下列各图中的直角三角形与Rt△ABC 全等的是( )
A
小试牛刀
3 如图,在△ABC 中,AB=CB,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF.
(1)求证:Rt△ABE ≌ Rt△CBF;
(2)若∠CAE=30°,求∠ACF 的度数.
小试牛刀
∵∠ABC=90°,
∴∠CBF=∠ABE=90°.
在Rt△ABE 和Rt△CBF 中,
∵AE=CF,AB=CB,
∴Rt△ABE ≌ Rt△CBF (HL).
(1)证明:
小试牛刀
∵AB=CB,∠ABC=90°,
∴∠CAB=∠ACB=45°.
∴∠BAE=∠CAB-∠CAE=45°-30°=15°.
由(1)知Rt△ABE ≌ Rt△CBF,
∴∠BCF=∠BAE=15°.
∴∠ACF=∠BCF+∠ACB=15°+45°=60°.
(2)解:
小试牛刀
4 如图,在△ABC 中,∠ACB=90°,AC=BC,直线MN 经过点C,且AD⊥MN 于D,BE⊥MN 于E.
求证:DE=AD+BE.
小试牛刀
∵∠ACB=90°,∴∠ACD+∠BCE=90°.
又∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°.
∴∠ACD+∠DAC=90°.∴∠BCE=∠CAD.
在△ADC 和△CEB 中,
∵∠CAD=∠BCE,∠ADC=∠CEB,AC=CB,
∴△ADC ≌ △CEB (AAS).
∴AD=CE,DC=EB.
又∵DE=CE+DC,∴DE=AD+BE.
证明:
小试牛刀
5 如图,已知AB=AE,∠B=∠E,BC=ED,AF⊥CD.
求证:F 是CD 的中点.
小试牛刀
如图,连接AC,AD.在△ABC 和△AED 中,
AB=AE,
∠B=∠E,
BC=ED,
∴△ABC ≌ △AED (SAS).
∴AC=AD.
又∵AF⊥CD,
∴CF=DF.
即F 为CD 的中点.
证明:
小试牛刀
6 感知:如图①,AD 平分∠BAC. ∠B+∠C=180°,∠B=90°,易知DB=DC.
探究:如图②,AD 平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图③,在四边形ABDC 中,∠B=45°,∠C=135°,DB=DC=a,则AB-AC=________(用含a 的代数式表示)
小试牛刀
如图,过点D 作DE⊥AB 于E,
DF⊥AC 交AC 的延长线于F.
∵AD 平分∠BAC,DE⊥AB,DF⊥AC,
∴∠DAC=∠DAB,∠F=∠AED=90°.
又∵AD=AD,
∴△AFD ≌ △AED.
∴DE=DF.
∵∠B+∠ACD=180°,
∠ACD+∠FCD=180°,
∴∠B=∠FCD.
证明:
小试牛刀
在△DFC 和△DEB 中,
∠F=∠DEB=90°,
∠FCD=∠B,
DF=DE,
∴△DFC ≌ △DEB.
∴DC=DB.
课堂小结
课堂小结
1.直角三角形的判定方法:
边边边、边角边、角边角、角角边、
斜边、直角边.
课堂小结
2. 判定直角三角形全等的“四种思路”:
(1)若已知条件中有一组直角边和一组斜边分别相等,
用“HL”判定.
(2)若有一组锐角和斜边分别相等,用“AAS”判定.
(3)若有一组锐角和一组直角边分别相等,①直角边是锐
角的对边,用“AAS”判定;②直角边是锐角的邻边,
用“ASA”判定.
(4)若有两组直角边分别相等,用“SAS”判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
