【班海精品】北师大版(新)八年级下-6.4多边形的内角和与外角和【优质教案】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-6.4多边形的内角和与外角和【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:42 | ||
图片预览

文档简介
班海数学精批——一本可精细批改的教辅
多边形的内角和
[教学目标]
〔知识与技能〕
1、了解多边形的内角、外角等概念;
2、能通过不同方法探索多边形的内角公式,并会应用它们进行有关计算.
〔过程与方法〕
在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯
〔情感、态度与价值观〕
体会数学与现实生活的联系,增强克服困难的勇气和信心
[重点难点]多边形的内角和与多边形的外角和公式是重点;多边形的内角和定理的推导是难点。
[教学过程]
一、复习导入
我们已经证明了三角形的内角和为180°,在小学我们用量角器量过四边形的内角的度数,知道四边形内角的和为360°,现在你能利用三角形的内角和定理证明吗?
二、多边形的内角和
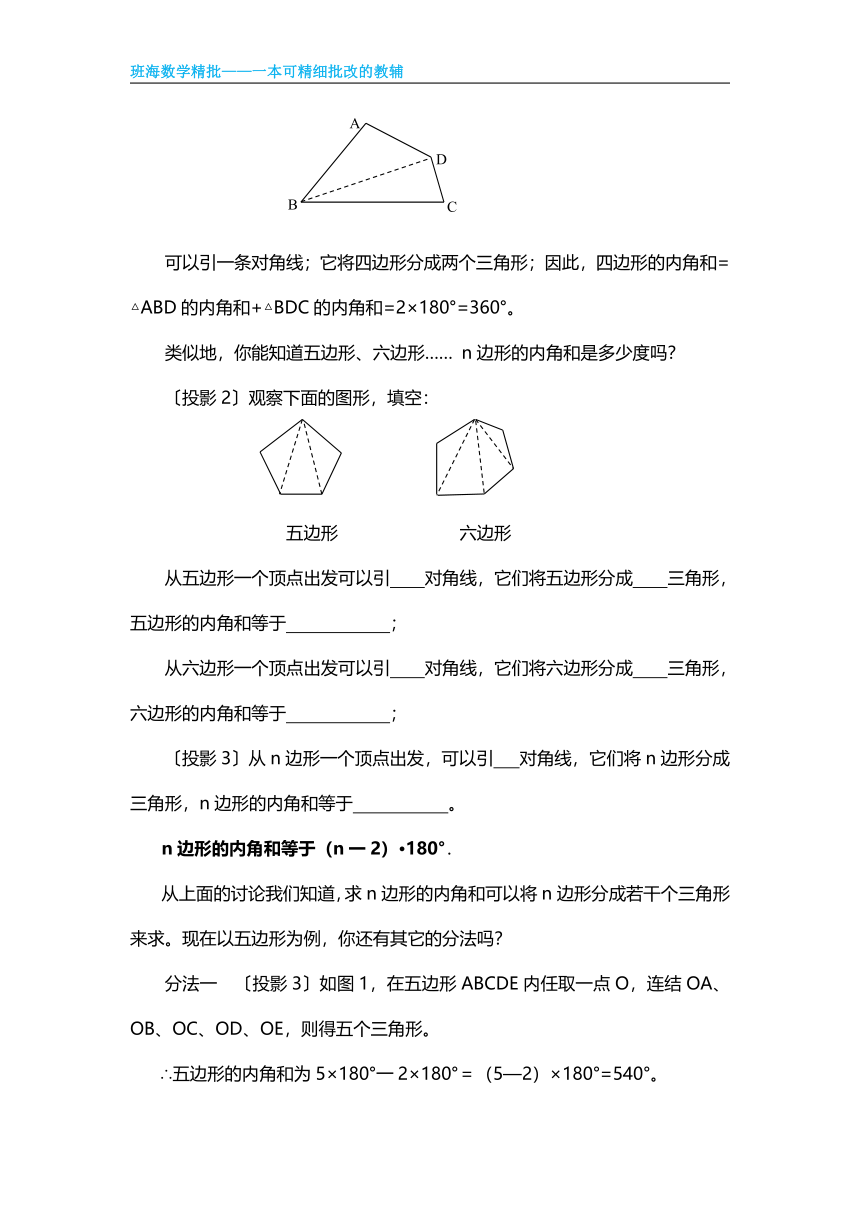
〔投影1〕如图,从四边形的一个顶点出发可以引几条对角线?它们将四边形分成几个三角形?那么四边形的内角和等于多少度?
可以引一条对角线;它将四边形分成两个三角形;因此,四边形的内角和=△ABD的内角和+△BDC的内角和=2×180°=360°。
类似地,你能知道五边形、六边形…… n边形的内角和是多少度吗?
〔投影2〕观察下面的图形,填空:
五边形 六边形
从五边形一个顶点出发可以引 对角线,它们将五边形分成 三角形,五边形的内角和等于 ;
从六边形一个顶点出发可以引 对角线,它们将六边形分成 三角形,六边形的内角和等于 ;
〔投影3〕从n边形一个顶点出发,可以引 对角线,它们将n边形分成 三角形,n边形的内角和等于 。
n边形的内角和等于(n一2)·180°.
从上面的讨论我们知道,求n边形的内角和可以将n边形分成若干个三角形来求。现在以五边形为例,你还有其它的分法吗?
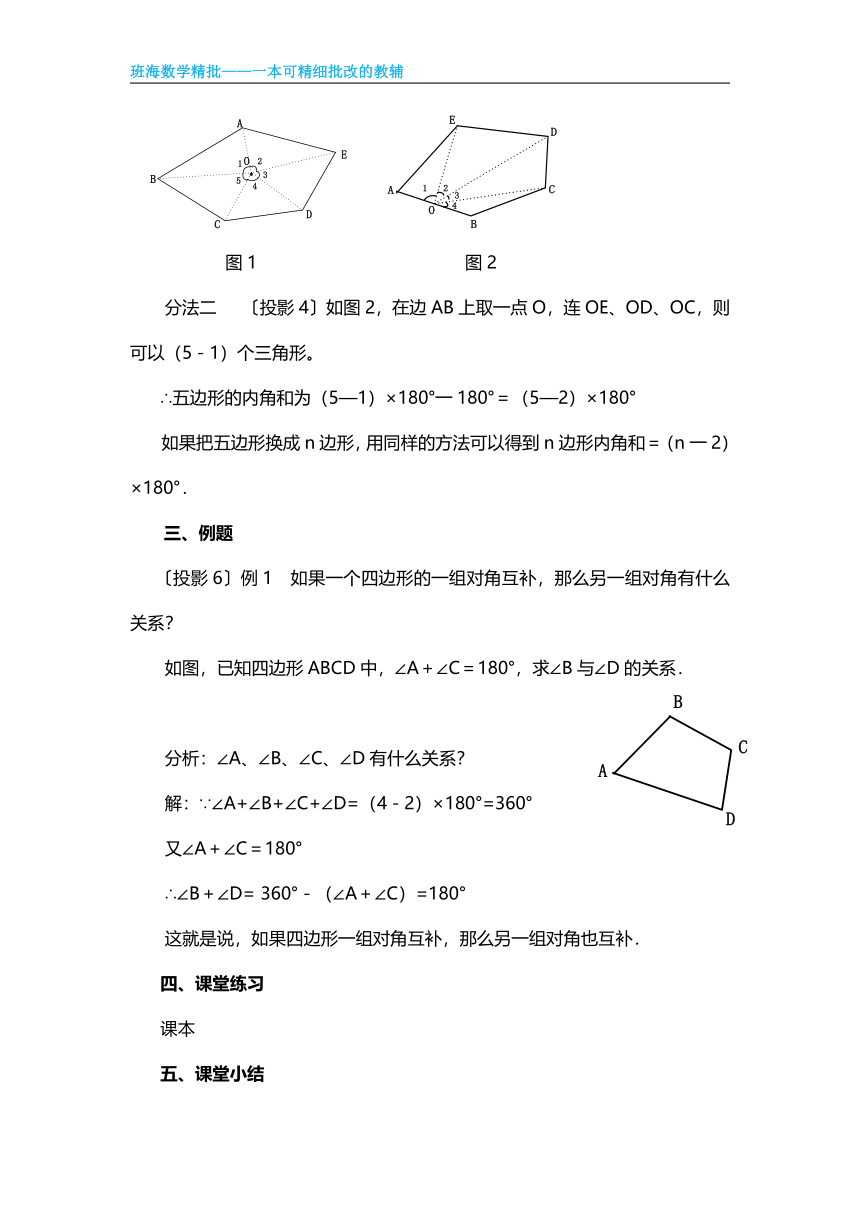
分法一 〔投影3〕如图1,在五边形ABCDE内任取一点O,连结OA、OB、OC、OD、OE,则得五个三角形。
∴五边形的内角和为5×180°一2×180°=(5—2)×180°=540°。
图1 图2
分法二 〔投影4〕如图2,在边AB上取一点O,连OE、OD、OC,则可以(5-1)个三角形。
∴五边形的内角和为(5—1)×180°一180°=(5—2)×180°
如果把五边形换成n边形,用同样的方法可以得到n边形内角和=(n一2)×180°.
三、例题
〔投影6〕例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
如图,已知四边形ABCD中,∠A+∠C=180°,求∠B与∠D的关系.
分析:∠A、∠B、∠C、∠D有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°=360°
又∠A+∠C=180°
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说,如果四边形一组对角互补,那么另一组对角也互补.
四、课堂练习
课本
五、课堂小结
n边形的内角和是多少度?
六、作业:
七、教后记
三角形的外角和
【教学目标】
1. 掌握多边形的外角和;
1. 掌握多边形外角和的推导方法;
1. 结合实践与应用,体会多边形内角和、外角和相互关系及转化。
【教学重点】
多边形外角和的定理
【教学难点】
结合实践与应用,体会多边形内角和、外角和相互关系及转化。
【教学过程】
1、 情境创设
1. 复习:三角形的外角的定义。
结论:三角形的一个外角等于与它不相邻的两个内角的和。
如图:谁来计算
∠DAE+∠ECF+∠ABF的度数之和。
方法一:根据三角形一个外角等于和它不相邻的两个内角之和,可以知道:
∠DEA=∠2+∠3, ∠ECF=∠2+∠1, ∠ABF=∠1+∠3
∴∠DAE+∠ECF+∠ABF=2(∠1+∠2+∠3)=3600.
于是有:三角形的三个外角之和是3600。
1、 探究新知
1.根据三角形外角的定义,类似地:多边形的一边与另
一边的延长线所组成的角,叫做多边形的外角。
那么谁来说说四边形ABCD的外角∠1+∠2+∠3+∠4的和是多少呢?
不妨来看看三角形的外角和的另一种算法:
如图:∠1+∠α=1800 ∠2+∠β=1800
∠3+∠γ=1800
于是∠1+∠α+∠2+∠β+∠3+∠γ=1800×3
又∠1+∠2+∠3=1800,
∴∠α+∠β+∠γ=3600.
2.同样,类似地有:
学生板演,得出四边形的外角和为3600.
引申为:n边形中,每个内角与相邻的外角都是互补关系,共有n组,于是内外角总和为n×1800,其内角和为(n-2)×1800,那么外角和为3600.
3.得出结论:任意多边形的外角和为3600.
三、例题讲解
解答题:
1. 一个多边形的内角和是外角和的3倍,求这个多边形的边数。
1. 一个多边形的每一个外角都是600,求这个多边形的内角和。
1. 一个多边形所有内角与它的一个外角的和等于20000,求这个外角的度数。
注重方程思想的渗透和分析问题解决问题的能力训练。
四、课堂练习
P31. 10
五、课堂小结
1).外角和的推导过程
2).外角和定理的应用
3).猜想:多边形的外角中,最多能有几个角是钝角?
六、课后作业
《补充习题》P11-12。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
A
B
C
D
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
多边形的内角和
[教学目标]
〔知识与技能〕
1、了解多边形的内角、外角等概念;
2、能通过不同方法探索多边形的内角公式,并会应用它们进行有关计算.
〔过程与方法〕
在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,逐步养成数学推理的习惯
〔情感、态度与价值观〕
体会数学与现实生活的联系,增强克服困难的勇气和信心
[重点难点]多边形的内角和与多边形的外角和公式是重点;多边形的内角和定理的推导是难点。
[教学过程]
一、复习导入
我们已经证明了三角形的内角和为180°,在小学我们用量角器量过四边形的内角的度数,知道四边形内角的和为360°,现在你能利用三角形的内角和定理证明吗?
二、多边形的内角和
〔投影1〕如图,从四边形的一个顶点出发可以引几条对角线?它们将四边形分成几个三角形?那么四边形的内角和等于多少度?
可以引一条对角线;它将四边形分成两个三角形;因此,四边形的内角和=△ABD的内角和+△BDC的内角和=2×180°=360°。
类似地,你能知道五边形、六边形…… n边形的内角和是多少度吗?
〔投影2〕观察下面的图形,填空:
五边形 六边形
从五边形一个顶点出发可以引 对角线,它们将五边形分成 三角形,五边形的内角和等于 ;
从六边形一个顶点出发可以引 对角线,它们将六边形分成 三角形,六边形的内角和等于 ;
〔投影3〕从n边形一个顶点出发,可以引 对角线,它们将n边形分成 三角形,n边形的内角和等于 。
n边形的内角和等于(n一2)·180°.
从上面的讨论我们知道,求n边形的内角和可以将n边形分成若干个三角形来求。现在以五边形为例,你还有其它的分法吗?
分法一 〔投影3〕如图1,在五边形ABCDE内任取一点O,连结OA、OB、OC、OD、OE,则得五个三角形。
∴五边形的内角和为5×180°一2×180°=(5—2)×180°=540°。
图1 图2
分法二 〔投影4〕如图2,在边AB上取一点O,连OE、OD、OC,则可以(5-1)个三角形。
∴五边形的内角和为(5—1)×180°一180°=(5—2)×180°
如果把五边形换成n边形,用同样的方法可以得到n边形内角和=(n一2)×180°.
三、例题
〔投影6〕例1 如果一个四边形的一组对角互补,那么另一组对角有什么关系?
如图,已知四边形ABCD中,∠A+∠C=180°,求∠B与∠D的关系.
分析:∠A、∠B、∠C、∠D有什么关系?
解:∵∠A+∠B+∠C+∠D=(4-2)×180°=360°
又∠A+∠C=180°
∴∠B+∠D= 360°-(∠A+∠C)=180°
这就是说,如果四边形一组对角互补,那么另一组对角也互补.
四、课堂练习
课本
五、课堂小结
n边形的内角和是多少度?
六、作业:
七、教后记
三角形的外角和
【教学目标】
1. 掌握多边形的外角和;
1. 掌握多边形外角和的推导方法;
1. 结合实践与应用,体会多边形内角和、外角和相互关系及转化。
【教学重点】
多边形外角和的定理
【教学难点】
结合实践与应用,体会多边形内角和、外角和相互关系及转化。
【教学过程】
1、 情境创设
1. 复习:三角形的外角的定义。
结论:三角形的一个外角等于与它不相邻的两个内角的和。
如图:谁来计算
∠DAE+∠ECF+∠ABF的度数之和。
方法一:根据三角形一个外角等于和它不相邻的两个内角之和,可以知道:
∠DEA=∠2+∠3, ∠ECF=∠2+∠1, ∠ABF=∠1+∠3
∴∠DAE+∠ECF+∠ABF=2(∠1+∠2+∠3)=3600.
于是有:三角形的三个外角之和是3600。
1、 探究新知
1.根据三角形外角的定义,类似地:多边形的一边与另
一边的延长线所组成的角,叫做多边形的外角。
那么谁来说说四边形ABCD的外角∠1+∠2+∠3+∠4的和是多少呢?
不妨来看看三角形的外角和的另一种算法:
如图:∠1+∠α=1800 ∠2+∠β=1800
∠3+∠γ=1800
于是∠1+∠α+∠2+∠β+∠3+∠γ=1800×3
又∠1+∠2+∠3=1800,
∴∠α+∠β+∠γ=3600.
2.同样,类似地有:
学生板演,得出四边形的外角和为3600.
引申为:n边形中,每个内角与相邻的外角都是互补关系,共有n组,于是内外角总和为n×1800,其内角和为(n-2)×1800,那么外角和为3600.
3.得出结论:任意多边形的外角和为3600.
三、例题讲解
解答题:
1. 一个多边形的内角和是外角和的3倍,求这个多边形的边数。
1. 一个多边形的每一个外角都是600,求这个多边形的内角和。
1. 一个多边形所有内角与它的一个外角的和等于20000,求这个外角的度数。
注重方程思想的渗透和分析问题解决问题的能力训练。
四、课堂练习
P31. 10
五、课堂小结
1).外角和的推导过程
2).外角和定理的应用
3).猜想:多边形的外角中,最多能有几个角是钝角?
六、课后作业
《补充习题》P11-12。
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
A
B
C
D
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
