【班海精品】北师大版(新)八年级下-6.2平行四边形的判定 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-6.2平行四边形的判定 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:42 | ||
图片预览








文档简介
(共42张PPT)
2.平行四边形的判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平行四边形的判定方法有哪些?
复
习
回
顾
新课精讲
探索新知
1
知识点
由对角线互相平分判定平行四边形
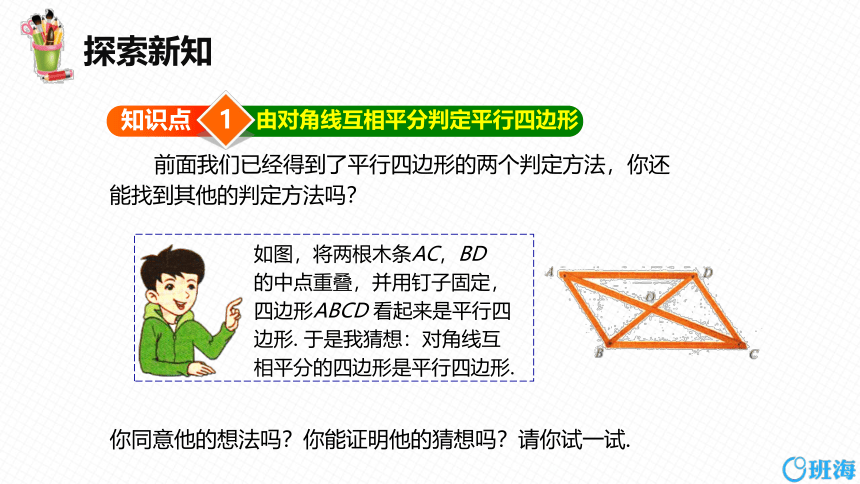
前面我们已经得到了平行四边形的两个判定方法,你还
能找到其他的判定方法吗?
你同意他的想法吗?你能证明他的猜想吗?请你试一试.
如图,将两根木条AC,BD
的中点重叠,并用钉子固定,
四边形ABCD 看起来是平行四
边形. 于是我猜想:对角线互
相平分的四边形是平行四边形.
探索新知
定理 对角线互相平分的四边形是平行四边形.
归 纳
探索新知
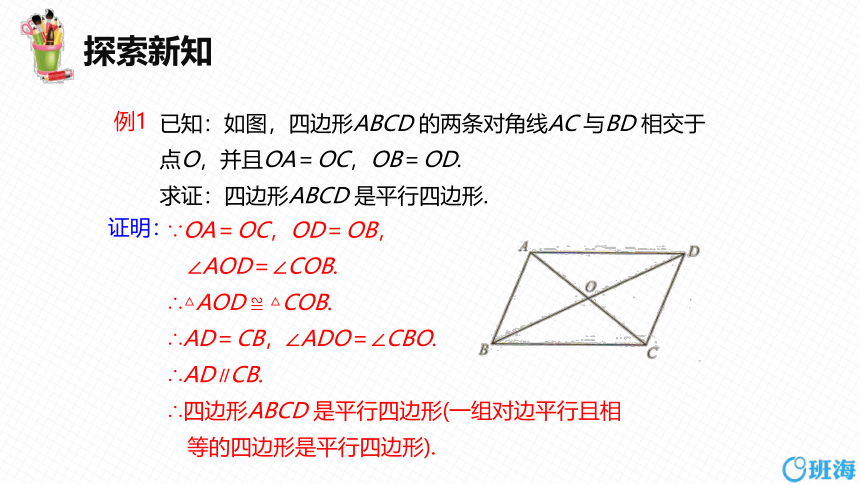
例1
已知:如图,四边形ABCD 的两条对角线AC 与BD 相交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD 是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB.
∴△AOD ≌ △COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD 是平行四边形(一组对边平行且相
等的四边形是平行四边形).
证明:
探索新知
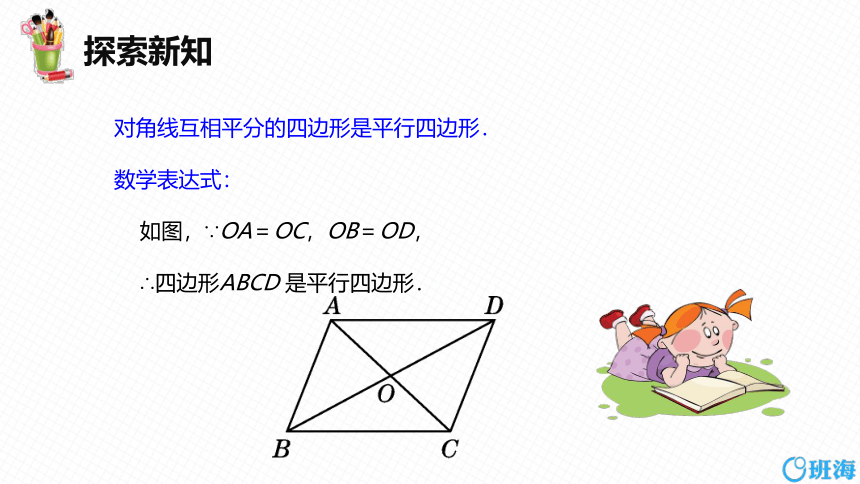
对角线互相平分的四边形是平行四边形.
数学表达式:
如图,∵OA=OC,OB=OD,
∴四边形ABCD 是平行四边形.
探索新知
例2
已知:如图(1),E,F 是 ABCD 对角线AC 上的两点,且AE=CF.
求证:四边形BFDE 是平行四边形.
探索新知
证明:
如图(2),连接BD,交AC 于点O.
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD (平行
四边形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE 是平行四边形(对角线互相平分的
四边形是平行四边形).
典题精讲
如图,在 ABCD 中,对角线AC 与BD 相交于点O,点E,F 分别是OA 和OC 的中点,四边形BFDE 是平行四边形吗?
请说明理由.
1
四边形BFDE 是平行四边形,
理由:∵四边形ABCD 是平行四边形,
∴OB=OD,OA=OC.
又∵E,F 分别是OA 和OC 的中点,
∴OE=OF. ∴四边形BFDE 是平行四边形.
解:
B
C
D
典题精讲
如图,四边形ABCD 的对角线相交于点O,AO=CO,请添加一个条件_______________________(只添一个即可),使四边形ABCD 是平行四边形.
2
BO=DO (答案不唯一)
典题精讲
如图,在四边形ABCD 中,对角线AC,BD 相交于点O,下列条件不能判定四边形ABCD 为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
3
C
探索新知
2
知识点
平行四边形判定方法的综合应用
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
探索新知
例3
如图,四边形ABCD 是平行四边形,E,F 为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
导引:
欲证明∠1=∠2,只需证得
四边形EDFB 是平行四边形
或△ABF ≌ △CDE 即可.
探索新知
(1)补充条件①BE∥DF.
证明:∵BE∥DF,
∴∠BEC=∠DFA. ∴∠BEA=∠DFC.
∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD. ∴∠BAE=∠DCF.
在△ABE 与△CDF 中,
∴△ABE ≌ △CDF (AAS).
∴BE=DF. ∴四边形BFDE 是平行四边形.
∴ED∥BF. ∴∠1=∠2.
解:
探索新知
(2)补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF 与△CDE 中,
∴△ABF ≌ △CDE (SAS).
∴∠1=∠2.
典题精讲
如图,在 ABCD 中,∠ABC=70°,∠ABC 的平分线交AD 于点E,过点D 作BE 的平行线交BC 于点F,求∠CDF 的度数.
1
A
B
C
D
E
F
典题精讲
∵四边形ABCD 是平行四边形,
∴AD∥BC,∠ABC=∠ADC.
∴ED∥BF. 又∵BE∥DF,
∴四边形BEDF 是平行四边形.
∴∠EBF=∠FDE.
∵∠ABC=70°,BE 平分∠ABC,
∴∠EBF= ∠ABC=35°.∴∠FDE=35°.
∵∠ABC=∠ADC,
∴∠CDF=∠ADC-∠FDE=35°.
解:
典题精讲
2 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
典题精讲
3 在四边形ABCD 中,AC 交BD 于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD ”,那么四边形ABCD 一定是平行四边形;②如果再加上条件“∠BAD=∠BCD ”,那么四边形ABCD 一定是平行四边形;③如果再加上条件“AO=OC ”,那么四边形ABCD 一定是平行四边形; ④如果再加上条件“∠DBA=∠CAB ”,那么四边形ABCD 一定是平行四边形.
其中正确的说法是( )
A.①② B.①③④ C.②③ D.②③④
C
典题精讲
4 在四边形ABCD 中,对角线AC,BD 相交于点O,给出下列4组条件:
①AB∥CD,AD∥BC; ②AB=CD,AD=BC;
③AO=CO,BO=DO;④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
C
易错提醒
如图,在 ABCD 中,对角线AC,BD 相交于O,E,F 是对角线AC 上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF. 其中不能判定四边形DEBF 是平行四边形的有( )
A.0个 B.1个
C.2个 D.3个
易错点:混淆平行四边形的判定方法致判断错误
B
易错提醒
给出条件①OE=OF,
由四边形ABCD 是平行四边形,可得OD=OB.
又∵OE=OF,∴四边形DEBF 为平行四边形.
故③正确.故①正确.故③正确.
给出条件③∠ADE=∠CBF,
∵四边形ABCD 是平行四边形,
∴AD=CB,AD∥CB.∴∠DAE=∠BCF.
又∵∠ADE=∠CBF,∴△ADE ≌ △CBF.
∴DE=BF,∠AED=∠CFB.
易错提醒
∴∠DEO=∠BFO.∴DE∥BF.
∴四边形DEBF 为平行四边形.故③正确.
给出条件④∠ABE=∠CDF,理由同③,亦可判定四边形DEBF 为平行四边形.故④正确.只有给出条件②无法判定四边形DEBF 为平行四边形.故选B.本题易错选A.将DE=BF 作为条件判定三角形全等,从而推出四边形DEBF 为平行四边形.
学以致用
小试牛刀
如图,在 ABCD 中,对角线AC,BD 相交于点O,E,F 是对角线AC 上的两点,当点E,F 满足下列哪个条件时,四边形DEBF 不一定是平行四边形( )
A.OE=OF
B.DF=BE
C.AE=CF
D.∠AEB=∠CFD
1
B
小试牛刀
如图,在四边形ABCD 中,对角线AC,BD 相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD 的面积为( )
A.6
B.12
C.20
D.24
2
D
小试牛刀
3 如图,在四边形ABCD 中,AB∥CD,E 是BC 的中点,AE 交DC 的延长线于点F. 试判断四边形ABFC 的形状,并说明理由.
小试牛刀
四边形ABFC 是平行四边形.理由如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E 是BC 的中点,∴BE=CE.
在△ABE 和△FCE 中,
∠BAE=∠CFE,
∠AEB=∠FEC,
BE=CE,
∴△ABE ≌ △FCE (AAS).∴AE=FE.
又∵BE=CE,∴四边形ABFC 是平行四边形.
解:
小试牛刀
4 如图,在 ABCD 中,点E,F 在对角线AC 上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF 是平行四边形.
小试牛刀
(1)∵四边形ABCD 是平行四边形,
∴AD∥CB,AD=CB. ∴∠DAE=∠BCF.
在△ADE 和△CBF 中,
AD=CB,
∠DAE=∠BCF,
AE=CF,
∴△ADE ≌ △CBF.
∴DE=BF.
证明:
小试牛刀
(2)如图,连接BD,交AC 于点O.
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,
∴OE=OF.
∴四边形DEBF 是平行四边形.
小试牛刀
5 如图,将 ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D ′ 处,直线l 交CD 边于点E,连接BE.
(1)求证:四边形BCED ′是平行四边形;
(2)若BE 平分∠ABC,求证:AB 2=AE 2+BE 2.
小试牛刀
(1)由折叠性质知∠DAE=∠D′AE,
∠D=∠AD′E.
∴∠AD′E=∠CBA.
∵四边形ABCD 为平行四边形,
∴AB∥CD,∠D=∠CBA.
∴ED ′∥CB.
∵EC∥D′B,
∴四边形BCED ′是平行四边形.
证明:
小试牛刀
(2)∵BE 平分∠ABC,
∴∠CBE=∠EBA.
又∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠DAB+∠CBA=180°.
∵∠DAE=∠BAE,
∴∠BAE+∠EBA=90°.
∴∠AEB=90°. ∴AB 2=AE 2+BE 2.
小试牛刀
6 如图,四边形ABCD 中,对角线AC,BD 相交于点O,点E,F 分别在OA,OC 上.
(1)给出以下条件:①OB=OD;②∠1=∠2;③OE=OF. 请你从中选取两个条件证明△BEO ≌ △DFO;
(2)在(1)中你所选条件的前提下,添加AE=CF,求证:四边形ABCD 是平行四边形.
小试牛刀
(1)选取①②.
在△BEO 和△DFO 中
∠1=∠2,
BO=DO,
∠EOB=∠FOD,
∴△BEO ≌ △DFO (ASA).
证明:
(2)由(1)得△BEO ≌ △DFO,
∴EO=FO.
∵AE=CF,
∴AO=CO.
又∵BO=DO,
∴四边形ABCD 是平行四边形.
课堂小结
课堂小结
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.平行四边形的判定
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平行四边形的判定方法有哪些?
复
习
回
顾
新课精讲
探索新知
1
知识点
由对角线互相平分判定平行四边形
前面我们已经得到了平行四边形的两个判定方法,你还
能找到其他的判定方法吗?
你同意他的想法吗?你能证明他的猜想吗?请你试一试.
如图,将两根木条AC,BD
的中点重叠,并用钉子固定,
四边形ABCD 看起来是平行四
边形. 于是我猜想:对角线互
相平分的四边形是平行四边形.
探索新知
定理 对角线互相平分的四边形是平行四边形.
归 纳
探索新知
例1
已知:如图,四边形ABCD 的两条对角线AC 与BD 相交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD 是平行四边形.
∵OA=OC,OD=OB,
∠AOD=∠COB.
∴△AOD ≌ △COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD 是平行四边形(一组对边平行且相
等的四边形是平行四边形).
证明:
探索新知
对角线互相平分的四边形是平行四边形.
数学表达式:
如图,∵OA=OC,OB=OD,
∴四边形ABCD 是平行四边形.
探索新知
例2
已知:如图(1),E,F 是 ABCD 对角线AC 上的两点,且AE=CF.
求证:四边形BFDE 是平行四边形.
探索新知
证明:
如图(2),连接BD,交AC 于点O.
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD (平行
四边形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE 是平行四边形(对角线互相平分的
四边形是平行四边形).
典题精讲
如图,在 ABCD 中,对角线AC 与BD 相交于点O,点E,F 分别是OA 和OC 的中点,四边形BFDE 是平行四边形吗?
请说明理由.
1
四边形BFDE 是平行四边形,
理由:∵四边形ABCD 是平行四边形,
∴OB=OD,OA=OC.
又∵E,F 分别是OA 和OC 的中点,
∴OE=OF. ∴四边形BFDE 是平行四边形.
解:
B
C
D
典题精讲
如图,四边形ABCD 的对角线相交于点O,AO=CO,请添加一个条件_______________________(只添一个即可),使四边形ABCD 是平行四边形.
2
BO=DO (答案不唯一)
典题精讲
如图,在四边形ABCD 中,对角线AC,BD 相交于点O,下列条件不能判定四边形ABCD 为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
3
C
探索新知
2
知识点
平行四边形判定方法的综合应用
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
探索新知
例3
如图,四边形ABCD 是平行四边形,E,F 为对角线AC上两点,连接ED,EB,FD,FB.给出以下结论:①BE∥DF;②BE=DF;③AE=CF.请你从中选取一个条件,使∠1=∠2成立,并给出证明.
导引:
欲证明∠1=∠2,只需证得
四边形EDFB 是平行四边形
或△ABF ≌ △CDE 即可.
探索新知
(1)补充条件①BE∥DF.
证明:∵BE∥DF,
∴∠BEC=∠DFA. ∴∠BEA=∠DFC.
∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD. ∴∠BAE=∠DCF.
在△ABE 与△CDF 中,
∴△ABE ≌ △CDF (AAS).
∴BE=DF. ∴四边形BFDE 是平行四边形.
∴ED∥BF. ∴∠1=∠2.
解:
探索新知
(2)补充条件③AE=CF.
证明:∵AE=CF,∴AF=CE.
∵四边形ABCD 是平行四边形,
∴AB=CD,AB∥CD.
∴∠BAF=∠DCE.
在△ABF 与△CDE 中,
∴△ABF ≌ △CDE (SAS).
∴∠1=∠2.
典题精讲
如图,在 ABCD 中,∠ABC=70°,∠ABC 的平分线交AD 于点E,过点D 作BE 的平行线交BC 于点F,求∠CDF 的度数.
1
A
B
C
D
E
F
典题精讲
∵四边形ABCD 是平行四边形,
∴AD∥BC,∠ABC=∠ADC.
∴ED∥BF. 又∵BE∥DF,
∴四边形BEDF 是平行四边形.
∴∠EBF=∠FDE.
∵∠ABC=70°,BE 平分∠ABC,
∴∠EBF= ∠ABC=35°.∴∠FDE=35°.
∵∠ABC=∠ADC,
∴∠CDF=∠ADC-∠FDE=35°.
解:
典题精讲
2 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
典题精讲
3 在四边形ABCD 中,AC 交BD 于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD ”,那么四边形ABCD 一定是平行四边形;②如果再加上条件“∠BAD=∠BCD ”,那么四边形ABCD 一定是平行四边形;③如果再加上条件“AO=OC ”,那么四边形ABCD 一定是平行四边形; ④如果再加上条件“∠DBA=∠CAB ”,那么四边形ABCD 一定是平行四边形.
其中正确的说法是( )
A.①② B.①③④ C.②③ D.②③④
C
典题精讲
4 在四边形ABCD 中,对角线AC,BD 相交于点O,给出下列4组条件:
①AB∥CD,AD∥BC; ②AB=CD,AD=BC;
③AO=CO,BO=DO;④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组 B.2组 C.3组 D.4组
C
易错提醒
如图,在 ABCD 中,对角线AC,BD 相交于O,E,F 是对角线AC 上的两点,给出下列4个条件:①OE=OF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF. 其中不能判定四边形DEBF 是平行四边形的有( )
A.0个 B.1个
C.2个 D.3个
易错点:混淆平行四边形的判定方法致判断错误
B
易错提醒
给出条件①OE=OF,
由四边形ABCD 是平行四边形,可得OD=OB.
又∵OE=OF,∴四边形DEBF 为平行四边形.
故③正确.故①正确.故③正确.
给出条件③∠ADE=∠CBF,
∵四边形ABCD 是平行四边形,
∴AD=CB,AD∥CB.∴∠DAE=∠BCF.
又∵∠ADE=∠CBF,∴△ADE ≌ △CBF.
∴DE=BF,∠AED=∠CFB.
易错提醒
∴∠DEO=∠BFO.∴DE∥BF.
∴四边形DEBF 为平行四边形.故③正确.
给出条件④∠ABE=∠CDF,理由同③,亦可判定四边形DEBF 为平行四边形.故④正确.只有给出条件②无法判定四边形DEBF 为平行四边形.故选B.本题易错选A.将DE=BF 作为条件判定三角形全等,从而推出四边形DEBF 为平行四边形.
学以致用
小试牛刀
如图,在 ABCD 中,对角线AC,BD 相交于点O,E,F 是对角线AC 上的两点,当点E,F 满足下列哪个条件时,四边形DEBF 不一定是平行四边形( )
A.OE=OF
B.DF=BE
C.AE=CF
D.∠AEB=∠CFD
1
B
小试牛刀
如图,在四边形ABCD 中,对角线AC,BD 相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD 的面积为( )
A.6
B.12
C.20
D.24
2
D
小试牛刀
3 如图,在四边形ABCD 中,AB∥CD,E 是BC 的中点,AE 交DC 的延长线于点F. 试判断四边形ABFC 的形状,并说明理由.
小试牛刀
四边形ABFC 是平行四边形.理由如下:
∵AB∥CD,∴∠BAE=∠CFE.
∵E 是BC 的中点,∴BE=CE.
在△ABE 和△FCE 中,
∠BAE=∠CFE,
∠AEB=∠FEC,
BE=CE,
∴△ABE ≌ △FCE (AAS).∴AE=FE.
又∵BE=CE,∴四边形ABFC 是平行四边形.
解:
小试牛刀
4 如图,在 ABCD 中,点E,F 在对角线AC 上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF 是平行四边形.
小试牛刀
(1)∵四边形ABCD 是平行四边形,
∴AD∥CB,AD=CB. ∴∠DAE=∠BCF.
在△ADE 和△CBF 中,
AD=CB,
∠DAE=∠BCF,
AE=CF,
∴△ADE ≌ △CBF.
∴DE=BF.
证明:
小试牛刀
(2)如图,连接BD,交AC 于点O.
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,
∴OE=OF.
∴四边形DEBF 是平行四边形.
小试牛刀
5 如图,将 ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D ′ 处,直线l 交CD 边于点E,连接BE.
(1)求证:四边形BCED ′是平行四边形;
(2)若BE 平分∠ABC,求证:AB 2=AE 2+BE 2.
小试牛刀
(1)由折叠性质知∠DAE=∠D′AE,
∠D=∠AD′E.
∴∠AD′E=∠CBA.
∵四边形ABCD 为平行四边形,
∴AB∥CD,∠D=∠CBA.
∴ED ′∥CB.
∵EC∥D′B,
∴四边形BCED ′是平行四边形.
证明:
小试牛刀
(2)∵BE 平分∠ABC,
∴∠CBE=∠EBA.
又∵四边形ABCD 是平行四边形,
∴AD∥BC.
∴∠DAB+∠CBA=180°.
∵∠DAE=∠BAE,
∴∠BAE+∠EBA=90°.
∴∠AEB=90°. ∴AB 2=AE 2+BE 2.
小试牛刀
6 如图,四边形ABCD 中,对角线AC,BD 相交于点O,点E,F 分别在OA,OC 上.
(1)给出以下条件:①OB=OD;②∠1=∠2;③OE=OF. 请你从中选取两个条件证明△BEO ≌ △DFO;
(2)在(1)中你所选条件的前提下,添加AE=CF,求证:四边形ABCD 是平行四边形.
小试牛刀
(1)选取①②.
在△BEO 和△DFO 中
∠1=∠2,
BO=DO,
∠EOB=∠FOD,
∴△BEO ≌ △DFO (ASA).
证明:
(2)由(1)得△BEO ≌ △DFO,
∴EO=FO.
∵AE=CF,
∴AO=CO.
又∵BO=DO,
∴四边形ABCD 是平行四边形.
课堂小结
课堂小结
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)对角线互相平分的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)一组对边平行且相等的四边形是平行四边形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
