【班海精品】北师大版(新)八年级下-6.3三角形的中位线【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-6.3三角形的中位线【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览









文档简介
(共44张PPT)
3.三角形的中位线
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
温故知新
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
新课精讲
探索新知
1
知识点
三角形中位线的性质
探究思考
请同学们按要求画图:
画任意△ABC 中,画AB、AC边中点D、E,连接DE.
D
E
定义:像DE 这样,连接三角形两边中点的线段叫做三角形的中位线.
探索新知
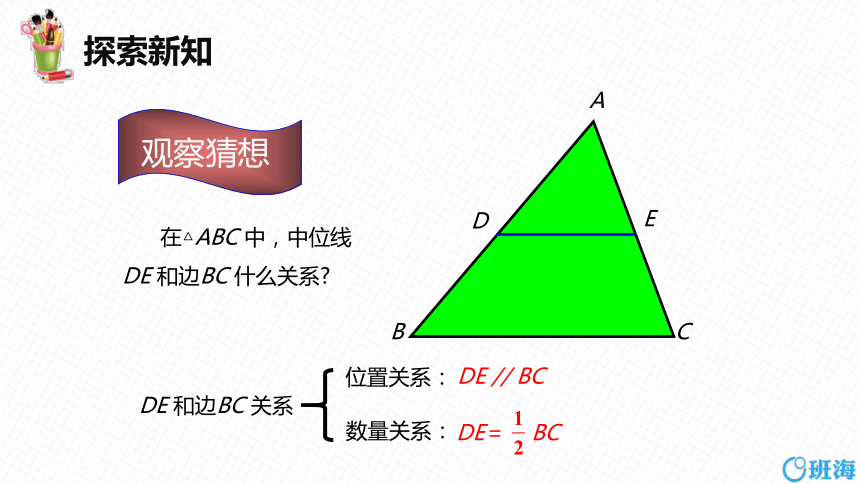
观察猜想
在△ABC 中,中位线DE 和边BC 什么关系
DE 和边BC 关系
数量关系:
位置关系:
A
B
C
D
E
DE // BC
DE= BC
探索新知
例1
如图(2),延长DE 到F,使FE=DE,连接CF.
在△ADE 和△CFE 中,
∵AE=CE,∠1=∠2,DE=FE,
∴△ADE ≌ △CFE.
∴∠A=∠ECF,AD=CF.
证明:
已知:如图(1),DE 是 △ABC 的中位线.
求证:DE∥BC,DE= BC.
探索新知
∴CF∥AB.
∵BD=AD,
∴CF=BD.
∴四边形DBCF 是平行四边形(一组对边平行且相等的四边形是平行四边形).
∴ DF∥BC (平行四边形的定义),
DF=BC (平行四边形的对边相等).
∴DE∥BC,DE= BC.
探索新知
利用三角形中位线定理可以证明小明分割的四个小三角形全等.
总 结
探索新知
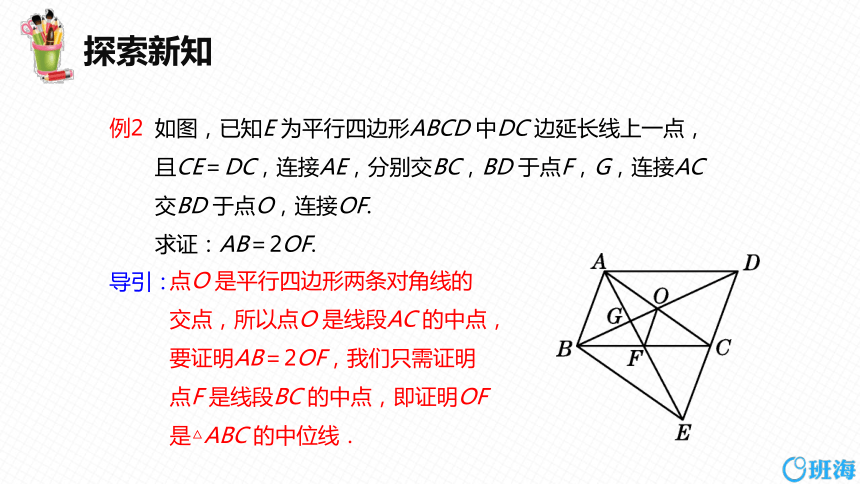
例2
如图,已知E 为平行四边形ABCD 中DC 边延长线上一点,且CE=DC,连接AE,分别交BC,BD 于点F,G,连接AC 交BD 于点O,连接OF.
求证:AB=2OF.
导引:
点O 是平行四边形两条对角线的
交点,所以点O 是线段AC 的中点,
要证明AB=2OF,我们只需证明
点F 是线段BC 的中点,即证明OF
是△ABC 的中位线.
探索新知
证明:
∵四边形ABCD 为平行四边形,
∴AB∥CD,AB=CD.
∵E 为平行四边形ABCD 中DC 边延长线上一点,
且CE=DC,
∴AB∥CE,AB=CE.
∴四边形ABEC 是平行四边形.
∴点F 是BC 的中点.
又∵点O 是AC 的中点,∴OF 是△ABC 的中位线.
∴AB=2OF.
探索新知
证明线段倍分关系的方法:
由于三角形的中位线等于三角形第三边的一半,因此当需要证明某一线段是另一线段的一半或两倍,且题中出现中点时,常考虑三角形中位线定理.
总 结
典题精讲
1
已知三角形的各边长分别为8 cm,10 cm和12 cm,
求以各边中点为顶点的三角形的周长.
解:
以各边中点为顶点的三角形的周长为
(8+10+12)=15(cm).
典题精讲
2
如图,A,B 两地被池塘隔开,小明通过下面的方法估
测出了A,B 间的距离:先在AB 外选一点C,然后步测
出AC,BC 的中点M,N,并步测出MN
的长,由此他就知道了A,B 间
的距离. 你能说说其中的道理吗?
解:
由题意可知,MN 是△ABC 的中位线,
所以AB=2MN.
所以测出MN 的长,就可知道A,B 间的距离.
A
典题精讲
3
如图,要测定被池塘隔开的A,B 两点的距离,可以在AB 外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m,DE=24 m,则AB=( )
A.50 m
B.48 m
C.45 m
D.35 m
B
典题精讲
4
如图,在△ABC 中,AB=3,BC=4,AC=2,D,E,F 分别为AB,BC,AC 的中点,连接DF,FE,则四边形DBEF 的周长是( )
A.5
B.7
C.9
D.11
B
探索新知
2
知识点
三角形中位线在四边形中的应用
议一议
如图,任意画一个四边形,以
四边的中点为顶点组成一个新
四边形,这个新四边形的形状
有什么特征?请证明你的结论,
并与同伴交流.
探索新知
中点四边形的定义:
依次连接任意四边形各边中点所得到的四边形称为中点四边形.
拓展:
不管四边形的形状怎样改变,中点四边形始终是平行四边形.
探索新知
例3
如图,在四边形ABCD 中,点E,F,G,H 分别是边AB,BC,CD,DA 的中点,连接EF,FG,GH,HE,得到四边形EFGH,求证:四边形EFGH 是平行四边形.
探索新知
如图,连接BD.
∵点E,H 分别是边AB,
DA 的中点,
∴EH 为△ABD 的中位线.
∴EH∥BD,EH= BD.
同理可得:FG∥BD,FG= BD.
∴EH∥FG,EH=FG.
∴四边形EFGH 是平行四边形.
证明:
探索新知
此题主要考查了平行四边形的判定及三角形中位线定理等知识,熟练掌握三角形中位线定理是解题的关键.
总 结
典题精讲
1
如图,已知E,F,G,H 分别为四边形ABCD 各边的中点,若AC=10 cm,BD=12 cm,则四边形EFGH 的周长为( )
A.10 cm
B.11 cm
C.12 cm
D.22 cm
D
典题精讲
2
如图,已知长方形ABCD 中,R,P 分别是DC,BC 上的点,E,F 分别是AP,RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,下列结论成立的是( )
A.线段EF 的长逐渐增大
B.线段EF 的长逐渐减小
C.线段EF 的长不改变
D.线段EF 的长先增大后减小
C
典题精讲
3
如图,在 ABCD 中,对角线AC,BD 相交于点O,点E 是AB 的中点,OE=5 cm,则AD 的长为______cm.
10
典题精讲
4
如图,四边形ABCD 中,∠A=90°,AB=3 ,AD=3,点M,N 分别为线段BC,AB 上的动点(含端点,但点M 不与点B 重合),点E,F 分别为DM,
MN 的中点,则EF 长度
的最大值为________.
3
易错提醒
如图, ABCD 的对角线AC,BD 相交于点O,点E,F 分别是线段AO,BO 的中点,若AC+BD=24 cm,△OAB 的周长是18 cm,则EF=________cm.
易错点:忽视整体思想的应用而求不出中位线的长
3
易错提醒
∵AC+BD=24 cm,
∴OA+OB=12 cm,
又∵△OAB 的周长是18 cm,
∴OA+OB+AB=18 cm,∴AB=6 cm.
又∵点E,F 分别是线段AO,BO 的中点,
∴EF= AB=3 cm.
此题易错之处在于忽视运用整体思想求OA,OB的长度和,从而导致求不出中位线长.
学以致用
小试牛刀
1
如图,△ABC 的面积是12,点D,E,F,G 分别是BC,AD,BE,CE 的中点,则△AFG 的面积是( )
A.4.5
B.5
C.5.5
D.6
A
小试牛刀
2
如图,在△ABC 中,AB=AC,E,F 分别是BC,AC 的中点,以AC 为斜边作 Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5°
B.DE 平分∠FDC
C.∠DEC=30°
D.AB= CD
C
小试牛刀
3 如图,在四边形ABCD 中,AB=DC,P 是对角线AC 的中点,M 是AD 的中点,N 是BC 的中点.
(1)若AB=6,求PM 的长;
(2)若∠PMN=20°,求∠MPN 的度数.
小试牛刀
(1)∵AB=DC,AB=6,∴DC=6.
∵点P 是AC 的中点,点M 是AD 的中点,
∴PM 是△ADC 的中位线.
∴PM= DC= ×6=3.
解:
小试牛刀
(2)∵点P 是AC 的中点,点N 是BC 的中点,
∴PN 是△ABC 的中位线.
∴PN= AB.
∵AB=DC,∴PM=PN.
∴∠PNM=∠PMN=20°.
∴∠MPN=180°-∠PMN-∠PNM=140°.
小试牛刀
4 如图,E 为 ABCD 中DC 边的延长线上一点,且CE=DC,连接AE,分别交BC,BD 于点F,G,连接AC 交BD 于O,连接OF,判断AB 与OF 的位置关系和数量关系,并证明你的结论.
小试牛刀
AB∥OF,OF= AB,
理由:如图,连接BE,
∵四边形ABCD 是平行四边形,
∴OA=OC,AB=DC,AB∥DE,
又∵CE=DC,∴AB=CE.
∴四边形ABEC 是平行四边形.
∴BF=CF.
∴OF 是△ABC 的中位线.
∴AB∥OF,OF= AB.
解:
小试牛刀
5 如图,四边形ABCD 中,AB=CD,G,H 分别是BC,AD 的中点,BA,CD 的延长线分别交GH 的延长线于点E,F. 求证:∠AEH=∠F.
小试牛刀
如图,连接AC,取AC 的中点M,连接HM,GM.
∵H 是AD 的中点,M 是AC 的中点,
∴HM 是△ADC 的中位线.
∴HM∥CD,HM= CD.
∴∠MHG=∠F.
同理,GM∥AB,GM= AB.
∴∠MGH=∠AEH.
又∵AB=CD,∴GM=HM.
∴∠MGH=∠MHG.∴∠AEH=∠F.
证明:
小试牛刀
当几个中点不是一个三角形的各边中点时,可设法再取一个中点,使它与已知中点能构成三角形的中位线.此题中H,G 分别是四边形ABCD 两条对边的中点,这时需连接对角线,将四边形转化为两个三角形,再取对角线中点,与已知中点相连,就会产生三角形的中位线,问题便迎刃而解.
小试牛刀
6 已知:如图,在 ABCD 中,E 是CD 的中点,F 是AE 的中点,FC 与BE 交于G. 求证:GF=GC.
小试牛刀
如图,取BE 的中点H,连接FH,CH.
∵F 是AE 的中点,H 是BE 的中点,
∴FH 是△ABE 的中位线.
∴FH∥AB 且FH= AB.
在 ABCD 中,AB∥DC,AB=DC.
又∵点E 是DC 的中点,
∴EC= DC= AB,∴FH=EC.
又∵AB∥DC,FH∥AB,∴FH∥EC,
∴四边形EFHC 是平行四边形.∴GF=GC.
证明:
课堂小结
课堂小结
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
几何语言(如图):
∵DE 是△ABC 的中位线,
∴DE∥BC.DE= BC.
A
B
C
D
E
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.三角形的中位线
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
温故知新
平行四边形的判定
边
角
对角线
两组对边分别平行的四边形是平行四边形
一组对边平行且相等的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
新课精讲
探索新知
1
知识点
三角形中位线的性质
探究思考
请同学们按要求画图:
画任意△ABC 中,画AB、AC边中点D、E,连接DE.
D
E
定义:像DE 这样,连接三角形两边中点的线段叫做三角形的中位线.
探索新知
观察猜想
在△ABC 中,中位线DE 和边BC 什么关系
DE 和边BC 关系
数量关系:
位置关系:
A
B
C
D
E
DE // BC
DE= BC
探索新知
例1
如图(2),延长DE 到F,使FE=DE,连接CF.
在△ADE 和△CFE 中,
∵AE=CE,∠1=∠2,DE=FE,
∴△ADE ≌ △CFE.
∴∠A=∠ECF,AD=CF.
证明:
已知:如图(1),DE 是 △ABC 的中位线.
求证:DE∥BC,DE= BC.
探索新知
∴CF∥AB.
∵BD=AD,
∴CF=BD.
∴四边形DBCF 是平行四边形(一组对边平行且相等的四边形是平行四边形).
∴ DF∥BC (平行四边形的定义),
DF=BC (平行四边形的对边相等).
∴DE∥BC,DE= BC.
探索新知
利用三角形中位线定理可以证明小明分割的四个小三角形全等.
总 结
探索新知
例2
如图,已知E 为平行四边形ABCD 中DC 边延长线上一点,且CE=DC,连接AE,分别交BC,BD 于点F,G,连接AC 交BD 于点O,连接OF.
求证:AB=2OF.
导引:
点O 是平行四边形两条对角线的
交点,所以点O 是线段AC 的中点,
要证明AB=2OF,我们只需证明
点F 是线段BC 的中点,即证明OF
是△ABC 的中位线.
探索新知
证明:
∵四边形ABCD 为平行四边形,
∴AB∥CD,AB=CD.
∵E 为平行四边形ABCD 中DC 边延长线上一点,
且CE=DC,
∴AB∥CE,AB=CE.
∴四边形ABEC 是平行四边形.
∴点F 是BC 的中点.
又∵点O 是AC 的中点,∴OF 是△ABC 的中位线.
∴AB=2OF.
探索新知
证明线段倍分关系的方法:
由于三角形的中位线等于三角形第三边的一半,因此当需要证明某一线段是另一线段的一半或两倍,且题中出现中点时,常考虑三角形中位线定理.
总 结
典题精讲
1
已知三角形的各边长分别为8 cm,10 cm和12 cm,
求以各边中点为顶点的三角形的周长.
解:
以各边中点为顶点的三角形的周长为
(8+10+12)=15(cm).
典题精讲
2
如图,A,B 两地被池塘隔开,小明通过下面的方法估
测出了A,B 间的距离:先在AB 外选一点C,然后步测
出AC,BC 的中点M,N,并步测出MN
的长,由此他就知道了A,B 间
的距离. 你能说说其中的道理吗?
解:
由题意可知,MN 是△ABC 的中位线,
所以AB=2MN.
所以测出MN 的长,就可知道A,B 间的距离.
A
典题精讲
3
如图,要测定被池塘隔开的A,B 两点的距离,可以在AB 外选一点C,连接AC,BC,并分别找出它们的中点D,E,连接ED. 现测得AC=30 m,BC=40 m,DE=24 m,则AB=( )
A.50 m
B.48 m
C.45 m
D.35 m
B
典题精讲
4
如图,在△ABC 中,AB=3,BC=4,AC=2,D,E,F 分别为AB,BC,AC 的中点,连接DF,FE,则四边形DBEF 的周长是( )
A.5
B.7
C.9
D.11
B
探索新知
2
知识点
三角形中位线在四边形中的应用
议一议
如图,任意画一个四边形,以
四边的中点为顶点组成一个新
四边形,这个新四边形的形状
有什么特征?请证明你的结论,
并与同伴交流.
探索新知
中点四边形的定义:
依次连接任意四边形各边中点所得到的四边形称为中点四边形.
拓展:
不管四边形的形状怎样改变,中点四边形始终是平行四边形.
探索新知
例3
如图,在四边形ABCD 中,点E,F,G,H 分别是边AB,BC,CD,DA 的中点,连接EF,FG,GH,HE,得到四边形EFGH,求证:四边形EFGH 是平行四边形.
探索新知
如图,连接BD.
∵点E,H 分别是边AB,
DA 的中点,
∴EH 为△ABD 的中位线.
∴EH∥BD,EH= BD.
同理可得:FG∥BD,FG= BD.
∴EH∥FG,EH=FG.
∴四边形EFGH 是平行四边形.
证明:
探索新知
此题主要考查了平行四边形的判定及三角形中位线定理等知识,熟练掌握三角形中位线定理是解题的关键.
总 结
典题精讲
1
如图,已知E,F,G,H 分别为四边形ABCD 各边的中点,若AC=10 cm,BD=12 cm,则四边形EFGH 的周长为( )
A.10 cm
B.11 cm
C.12 cm
D.22 cm
D
典题精讲
2
如图,已知长方形ABCD 中,R,P 分别是DC,BC 上的点,E,F 分别是AP,RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,下列结论成立的是( )
A.线段EF 的长逐渐增大
B.线段EF 的长逐渐减小
C.线段EF 的长不改变
D.线段EF 的长先增大后减小
C
典题精讲
3
如图,在 ABCD 中,对角线AC,BD 相交于点O,点E 是AB 的中点,OE=5 cm,则AD 的长为______cm.
10
典题精讲
4
如图,四边形ABCD 中,∠A=90°,AB=3 ,AD=3,点M,N 分别为线段BC,AB 上的动点(含端点,但点M 不与点B 重合),点E,F 分别为DM,
MN 的中点,则EF 长度
的最大值为________.
3
易错提醒
如图, ABCD 的对角线AC,BD 相交于点O,点E,F 分别是线段AO,BO 的中点,若AC+BD=24 cm,△OAB 的周长是18 cm,则EF=________cm.
易错点:忽视整体思想的应用而求不出中位线的长
3
易错提醒
∵AC+BD=24 cm,
∴OA+OB=12 cm,
又∵△OAB 的周长是18 cm,
∴OA+OB+AB=18 cm,∴AB=6 cm.
又∵点E,F 分别是线段AO,BO 的中点,
∴EF= AB=3 cm.
此题易错之处在于忽视运用整体思想求OA,OB的长度和,从而导致求不出中位线长.
学以致用
小试牛刀
1
如图,△ABC 的面积是12,点D,E,F,G 分别是BC,AD,BE,CE 的中点,则△AFG 的面积是( )
A.4.5
B.5
C.5.5
D.6
A
小试牛刀
2
如图,在△ABC 中,AB=AC,E,F 分别是BC,AC 的中点,以AC 为斜边作 Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是( )
A.∠ECD=112.5°
B.DE 平分∠FDC
C.∠DEC=30°
D.AB= CD
C
小试牛刀
3 如图,在四边形ABCD 中,AB=DC,P 是对角线AC 的中点,M 是AD 的中点,N 是BC 的中点.
(1)若AB=6,求PM 的长;
(2)若∠PMN=20°,求∠MPN 的度数.
小试牛刀
(1)∵AB=DC,AB=6,∴DC=6.
∵点P 是AC 的中点,点M 是AD 的中点,
∴PM 是△ADC 的中位线.
∴PM= DC= ×6=3.
解:
小试牛刀
(2)∵点P 是AC 的中点,点N 是BC 的中点,
∴PN 是△ABC 的中位线.
∴PN= AB.
∵AB=DC,∴PM=PN.
∴∠PNM=∠PMN=20°.
∴∠MPN=180°-∠PMN-∠PNM=140°.
小试牛刀
4 如图,E 为 ABCD 中DC 边的延长线上一点,且CE=DC,连接AE,分别交BC,BD 于点F,G,连接AC 交BD 于O,连接OF,判断AB 与OF 的位置关系和数量关系,并证明你的结论.
小试牛刀
AB∥OF,OF= AB,
理由:如图,连接BE,
∵四边形ABCD 是平行四边形,
∴OA=OC,AB=DC,AB∥DE,
又∵CE=DC,∴AB=CE.
∴四边形ABEC 是平行四边形.
∴BF=CF.
∴OF 是△ABC 的中位线.
∴AB∥OF,OF= AB.
解:
小试牛刀
5 如图,四边形ABCD 中,AB=CD,G,H 分别是BC,AD 的中点,BA,CD 的延长线分别交GH 的延长线于点E,F. 求证:∠AEH=∠F.
小试牛刀
如图,连接AC,取AC 的中点M,连接HM,GM.
∵H 是AD 的中点,M 是AC 的中点,
∴HM 是△ADC 的中位线.
∴HM∥CD,HM= CD.
∴∠MHG=∠F.
同理,GM∥AB,GM= AB.
∴∠MGH=∠AEH.
又∵AB=CD,∴GM=HM.
∴∠MGH=∠MHG.∴∠AEH=∠F.
证明:
小试牛刀
当几个中点不是一个三角形的各边中点时,可设法再取一个中点,使它与已知中点能构成三角形的中位线.此题中H,G 分别是四边形ABCD 两条对边的中点,这时需连接对角线,将四边形转化为两个三角形,再取对角线中点,与已知中点相连,就会产生三角形的中位线,问题便迎刃而解.
小试牛刀
6 已知:如图,在 ABCD 中,E 是CD 的中点,F 是AE 的中点,FC 与BE 交于G. 求证:GF=GC.
小试牛刀
如图,取BE 的中点H,连接FH,CH.
∵F 是AE 的中点,H 是BE 的中点,
∴FH 是△ABE 的中位线.
∴FH∥AB 且FH= AB.
在 ABCD 中,AB∥DC,AB=DC.
又∵点E 是DC 的中点,
∴EC= DC= AB,∴FH=EC.
又∵AB∥DC,FH∥AB,∴FH∥EC,
∴四边形EFHC 是平行四边形.∴GF=GC.
证明:
课堂小结
课堂小结
三角形的中位线平行于三角形的第三边,且等于第三边的一半.
几何语言(如图):
∵DE 是△ABC 的中位线,
∴DE∥BC.DE= BC.
A
B
C
D
E
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
