【班海精品】北师大版(新)八年级下-3.1图形的平移 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-3.1图形的平移 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:42 | ||
图片预览









文档简介
(共45张PPT)
1.图形的平移
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾反思
(2)经过平移后,对应点所连的线段 平行且相等;
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
1、平移的定义
2、平移的性质
(1)平移不改变图形的形状和大小,只改变形图形的位置
新课精讲
探索新知
1
知识点
左右平移的点的坐标变化规律
议一议
在平面直角坐标系中,一个点沿x 轴方向平移a
(a>0)个单位长度后的坐标是什么?
探索新知
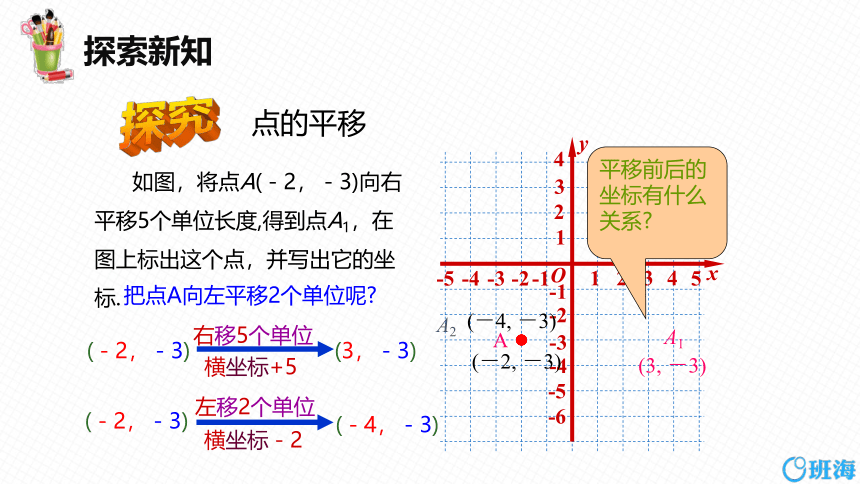
探究
如图,将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢
点的平移
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3, -3)
A
(-2, -3)
A2
(-4, -3)
(-2,-3)
右移5个单位
(3,-3)
横坐标+5
(-2,-3)
左移2个单位
(-4,-3)
横坐标-2
平移前后的坐标有什么关系
探索新知
(1)点(x,y )向左平移a (a>0)个单位 平移后的坐标为( x-a, y );
(2)点(x,y )向右平移a (a>0)个单位 平移后的坐标为( x+a,y );
探索新知
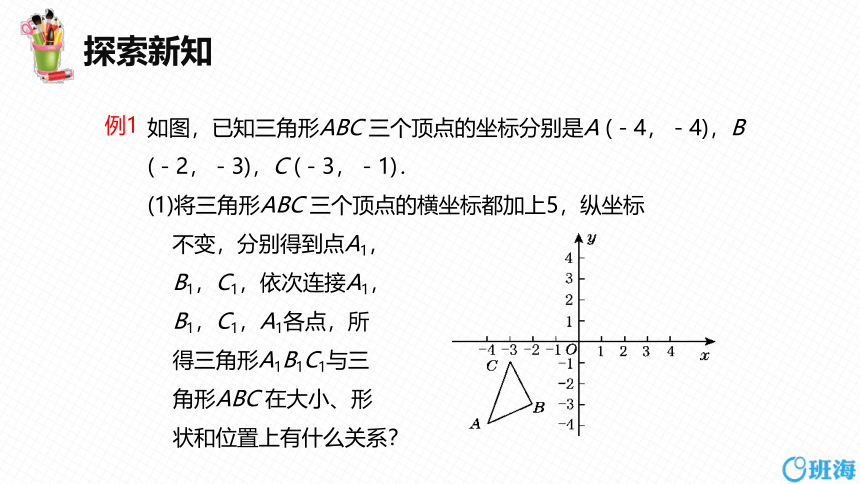
如图,已知三角形ABC 三个顶点的坐标分别是A (-4,-4),B (-2,-3),C (-3,-1).
(1)将三角形ABC 三个顶点的横坐标都加上5,纵坐标
不变,分别得到点A1,
B1,C1,依次连接A1,
B1,C1,A1各点,所
得三角形A1B1C1与三
角形ABC 在大小、形
状和位置上有什么关系?
例1
探索新知
(2)将三角形ABC 三个顶点的纵坐标都加上4,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2,A2各点,所得三角形A2B2C2与三角形ABC 在大小、形状和位置上有什么关系?
(1)纵坐标不变,横坐标加上5,就是将三角形ABC 向右平移5个单位长度;
(2)中的横坐标不变,纵坐标都加上4,就是将三角形ABC 向上平移4个单位长度.
导引:
探索新知
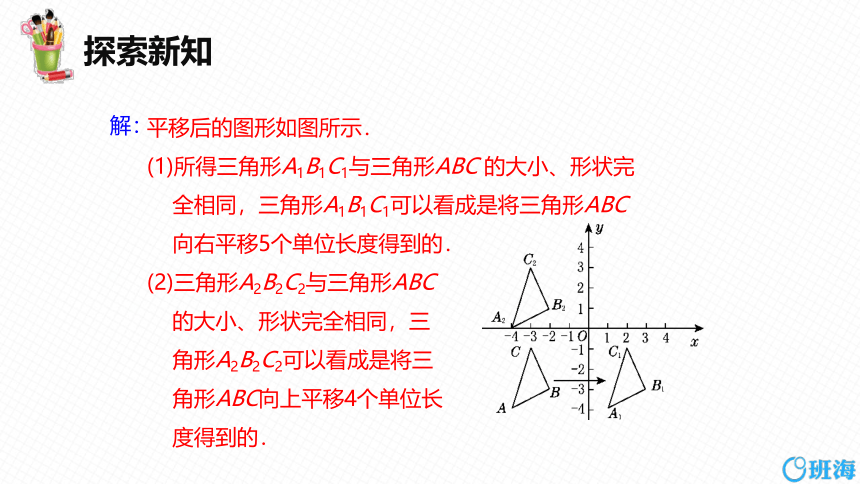
平移后的图形如图所示.
(1)所得三角形A1B1C1与三角形ABC 的大小、形状完
全相同,三角形A1B1C1可以看成是将三角形ABC
向右平移5个单位长度得到的.
(2)三角形A2B2C2与三角形ABC
的大小、形状完全相同,三
角形A2B2C2可以看成是将三
角形ABC向上平移4个单位长
度得到的.
解:
探索新知
总 结
从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移;横坐标的变化决定图形左右平移,纵坐标的变化决定图形上下平移.
典题精讲
四边形ABCD 的顶点坐标分别是A (0,3),B (-3,0),C (0,-3),D (3,0).
将四边形ABCD 向右平移6个单位长度,得到四边形A1B1C1D1,写出四边形A1B1C1D1各顶点的坐标;
1
解:A1(6,3),B1(3,0),C1(6,-3),D1(9,0).
典题精讲
在平面直角坐标系中,点P (-1,2)向右平移3个单位长度得到的点的坐标是________.
在平面直角坐标系xOy 中,线段AB 的两个端点分别为A (-1,-1),B (1,2),平移线段AB,得到线段A′B ′,已知A′的坐标为(3,-1),则点B ′的坐标为( )
A.(4,2) B.(5,2)
C.(6,2) D.(5,3)
2
3
(2,2)
B
典题精讲
如图,在平面直角坐标系中,平移△ABC 后,点A 的对应点A′的坐标为(-3,-2),则点B 的对应点B ′的坐标为( )
A.(2,1)
B.(2,2)
C.(1,0)
D.(1,3)
4
C
探索新知
2
知识点
上下平移的点的坐标变化规律
议一议
在平面直角坐标系中,一个点沿 y 轴方向平移a (a>0)个单位长度后的点的坐标是什么?
探索新知
探究
如图,将点A(-2, -3)向上平移6个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
点的平移
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A
(-2, -3)
把点A向下平移4个单位呢
A1
(-2, 3)
A2
(-2, -7)
(-2,-3)
上移6个单位
(-2,3)
纵坐标+6
(-2,-3)
下移4个单位
(-2,-7)
纵坐标-4
平移前后的坐标有什么关系?
探索新知
(1)点(x, y )向上平移a (a>0)个单位 平移后的坐标为(x,y+a );
(2)点(x,y )向下平移a (a>0)个单位 平移后的坐标为(x,y-a ).
典题精讲
1
解:A2(6,9),B2(3,6),C2(6,3),D2(9,6).
四边形ABCD 的顶点坐标分别是A (0,3),B (-3,0),C (0,-3),D (3,0).
将四边形A1B1C1D1向上平移6个单位长度,得到四边形A2B2C2D2,写出四边形A2B2C2D2各顶点的坐标.
典题精讲
将第1题中的四边形A2B2C2D2各顶点的纵坐标不变,横坐标分别减4,得到四边形為A3B3C3D3 ,它与四边形A2B2C2D2相比有什么变化?
2
解:将四边形A2B2C2D2向左平移4个单位长度,得到四边形
A3B3C3D3 ,形状、大小未发生变化.
典题精讲
将四边形A3B3C3D3各顶点的横坐标不变,纵坐标分别减4,得到四边形A4B4C4D4,它与四边形A3B3C3D3相比有什么变化?
3
解:将四边形A3B3C3D3向下平移4个单位长度,得到四
边形A4B4C4D4 ,形状、大小未发生变化.
典题精讲
在平面直角坐标系中,将三角形各点的纵坐标都减4,横坐标保持不变,所得图形与原图形相比,( )
A.向右平移了4个单位长度
B.向左平移了4个单位长度
C.向上平移了4个单位长度
D.向下平移了4个单位长度
4
D
典题精讲
如图,在平面直角坐标系中,将点M (2,1)向下平移2个单位长度得到点N,则点N 的坐标为( )
A.(2,-1)
B.(2,3)
C.(0,1)
D.(4,1)
5
A
典题精讲
6
若一个四边形上的其中一点P 在平移的过程中,坐标变化为P (x,y ) →P ′(x+3,y ),则该四边形的平移情况是( )
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
C
典题精讲
7
如图,与图①中的三角形相比,图②中的三角形发生的变化是( )
A.向左平移了3个单位长度
B.向右平移了1个单位长度
C.向上平移了3个单位长度
D.向下平移了1个单位长度
A
典题精讲
8
如图,△ABO 的顶点B 的坐标是(-2,0),将△ABO 沿 y 轴向上平移3个单位长度后,点B 的对应点的坐标是_____________.
(-2,3)
易错提醒
如图,△OAB 的顶点A 的坐标为(3,5),点B (4,0),把△OAB 沿x 轴向右平移得到
△CDE,如果CB=1,那么点
D 的坐标为________.
易错点:忽视平移性质中所有对应点的平移方向、
距离的关系而致错
(6,5)
易错提醒
∵点B (4,0),CB=1,∴OC=3.
∴△OAB 平移的距离为3.
∴点D 是由点A 向右平移3个单位长度得到的.
∴D 的坐标为(6,5).
本题易错之处在于忽视图形平移过程中所有对应点的平移方向、平移距离是一致的.
学以致用
小试牛刀
已知点A (-2,-1),将点A 沿x 轴方向平移2个单位长度得到点B,则点B 的坐标为( )
A.(-4,-1)
B.(0,-1)
C.(-4,-1)或(0,-1)
D.以上都不对
1
C
小试牛刀
如图,在平面直角坐标系中,△ABC 位于第二象限,点A 的坐标是(-2,3),先把△ABC 向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x 轴对称的△A2B2C2,则点A 的对应点A2的坐标是( )
A.(-3,2)
B.(2,-3)
C.(1,-2)
D.(-1,2)
2
B
小试牛刀
3
如图,将直线 y=-x 沿y 轴向下平移后的直线恰好经过点A (2,-4),且与y 轴交于点B,在x 轴上存在一点P
使得PA+PB 的值最小,则点
P 的坐标为________.
小试牛刀
4 如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P1.
(1)画出⊙P1;
(2)设⊙P1与x 轴正半轴,y 轴正半轴
的交点分别为A,B,求劣弧AB 与
弦AB 围成的图形的面积(结果保留π).
小试牛刀
(1)如图,⊙P1即为所求.
(2)如图,劣弧AB 与弦AB 围成的图形的面积为
解:
小试牛刀
5 在如图所示的直角坐标系中,解答下列问题:
(1)已知A (2,0),B (-1,-4),C (3,-3)三点,分别在坐标系中找出它们,并连接得到三角形ABC;
(2)将三角形ABC 向上平移4个单位长度,得到三角形A1B1C1;
(3)求三角形A1B1C1的面积.
小试牛刀
(1)如图.
(2)如图.
(3)三角形A1B1C1的面积为
4×4- ×4×1- ×1×3- ×3×4=6.5.
解:
小试牛刀
6 如图,点P (2a-12,1-a )位于第三象限,点Q (x,y )位于第二象限且是由点P 向上平移一定单位长度得到的.
(1)若点P 的纵坐标为-3,试求出a 的值;
(2)在(1)的条件下,试求出符合条件的一个Q 的坐标;
(3)若点P 的横、纵坐标都是整数,试求出a 的值以及线段PQ 长度的取值范围.
小试牛刀
(1)1-a=-3,a=4.
(2)由a=4得2a-12=2×4-12=-4.
又点Q (x,y )位于第二象限,所以y>0.
取y=1,得点Q 的坐标为(-4,1)
(答案不唯一,其他符合题意也可).
(3)因为点P (2a-12,1-a )位于第三象限,
所以
解得1<a<6.
解:
小试牛刀
因为点P 的横、纵坐标都是整数,
所以a=2 或 3或 4 或 5.
当a=2时,1-a=-1,
所以PQ>1;
当a=3时,1-a=-2,所以PQ>2;
当a=4时,1-a=-3,所以PQ>3;
当a=5时,1-a=-4,所以PQ>4.
小试牛刀
如图,在平面直角坐标系中,点A,B 在x 轴上,且A (-10,0),
AB=4,△ABC 的面积为14.将△ABC 沿x 轴向右平移得到△DEF,
当点D 为AB 中点时,点F 恰好在 y 轴上.求:
(1)点F 的坐标;
(2)△EOF 的面积.
小试牛刀
(1)∵A (-10,0),AB=4,
∴B (-6,0).
∵S△ABC= AB | yc |=14,
∴| yc |=7.
∵点C 在第二象限,∴yc=7.
∵△ABC 沿x 轴向右平移得到△DEF,点F 在 y 轴上,
∴F (0,7).
解:
小试牛刀
(2)∵A (-10,0),B (-6,0),D 为AB 中点,
∴D (-8,0).
∵DE=AB=4,
∴E (-4,0).∴OE=4.
∴S△EOF= OE OF= ×4×7=14.
课堂小结
课堂小结
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.图形的平移
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾反思
(2)经过平移后,对应点所连的线段 平行且相等;
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.
1、平移的定义
2、平移的性质
(1)平移不改变图形的形状和大小,只改变形图形的位置
新课精讲
探索新知
1
知识点
左右平移的点的坐标变化规律
议一议
在平面直角坐标系中,一个点沿x 轴方向平移a
(a>0)个单位长度后的坐标是什么?
探索新知
探究
如图,将点A(-2,-3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢
点的平移
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A1
(3, -3)
A
(-2, -3)
A2
(-4, -3)
(-2,-3)
右移5个单位
(3,-3)
横坐标+5
(-2,-3)
左移2个单位
(-4,-3)
横坐标-2
平移前后的坐标有什么关系
探索新知
(1)点(x,y )向左平移a (a>0)个单位 平移后的坐标为( x-a, y );
(2)点(x,y )向右平移a (a>0)个单位 平移后的坐标为( x+a,y );
探索新知
如图,已知三角形ABC 三个顶点的坐标分别是A (-4,-4),B (-2,-3),C (-3,-1).
(1)将三角形ABC 三个顶点的横坐标都加上5,纵坐标
不变,分别得到点A1,
B1,C1,依次连接A1,
B1,C1,A1各点,所
得三角形A1B1C1与三
角形ABC 在大小、形
状和位置上有什么关系?
例1
探索新知
(2)将三角形ABC 三个顶点的纵坐标都加上4,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2,A2各点,所得三角形A2B2C2与三角形ABC 在大小、形状和位置上有什么关系?
(1)纵坐标不变,横坐标加上5,就是将三角形ABC 向右平移5个单位长度;
(2)中的横坐标不变,纵坐标都加上4,就是将三角形ABC 向上平移4个单位长度.
导引:
探索新知
平移后的图形如图所示.
(1)所得三角形A1B1C1与三角形ABC 的大小、形状完
全相同,三角形A1B1C1可以看成是将三角形ABC
向右平移5个单位长度得到的.
(2)三角形A2B2C2与三角形ABC
的大小、形状完全相同,三
角形A2B2C2可以看成是将三
角形ABC向上平移4个单位长
度得到的.
解:
探索新知
总 结
从图形上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移;横坐标的变化决定图形左右平移,纵坐标的变化决定图形上下平移.
典题精讲
四边形ABCD 的顶点坐标分别是A (0,3),B (-3,0),C (0,-3),D (3,0).
将四边形ABCD 向右平移6个单位长度,得到四边形A1B1C1D1,写出四边形A1B1C1D1各顶点的坐标;
1
解:A1(6,3),B1(3,0),C1(6,-3),D1(9,0).
典题精讲
在平面直角坐标系中,点P (-1,2)向右平移3个单位长度得到的点的坐标是________.
在平面直角坐标系xOy 中,线段AB 的两个端点分别为A (-1,-1),B (1,2),平移线段AB,得到线段A′B ′,已知A′的坐标为(3,-1),则点B ′的坐标为( )
A.(4,2) B.(5,2)
C.(6,2) D.(5,3)
2
3
(2,2)
B
典题精讲
如图,在平面直角坐标系中,平移△ABC 后,点A 的对应点A′的坐标为(-3,-2),则点B 的对应点B ′的坐标为( )
A.(2,1)
B.(2,2)
C.(1,0)
D.(1,3)
4
C
探索新知
2
知识点
上下平移的点的坐标变化规律
议一议
在平面直角坐标系中,一个点沿 y 轴方向平移a (a>0)个单位长度后的点的坐标是什么?
探索新知
探究
如图,将点A(-2, -3)向上平移6个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
点的平移
x
y
O
1
2
3
4
2
4
1
3
-1
-2
-3
-4
-5
-1
-2
-3
-4
-5
5
-6
A
(-2, -3)
把点A向下平移4个单位呢
A1
(-2, 3)
A2
(-2, -7)
(-2,-3)
上移6个单位
(-2,3)
纵坐标+6
(-2,-3)
下移4个单位
(-2,-7)
纵坐标-4
平移前后的坐标有什么关系?
探索新知
(1)点(x, y )向上平移a (a>0)个单位 平移后的坐标为(x,y+a );
(2)点(x,y )向下平移a (a>0)个单位 平移后的坐标为(x,y-a ).
典题精讲
1
解:A2(6,9),B2(3,6),C2(6,3),D2(9,6).
四边形ABCD 的顶点坐标分别是A (0,3),B (-3,0),C (0,-3),D (3,0).
将四边形A1B1C1D1向上平移6个单位长度,得到四边形A2B2C2D2,写出四边形A2B2C2D2各顶点的坐标.
典题精讲
将第1题中的四边形A2B2C2D2各顶点的纵坐标不变,横坐标分别减4,得到四边形為A3B3C3D3 ,它与四边形A2B2C2D2相比有什么变化?
2
解:将四边形A2B2C2D2向左平移4个单位长度,得到四边形
A3B3C3D3 ,形状、大小未发生变化.
典题精讲
将四边形A3B3C3D3各顶点的横坐标不变,纵坐标分别减4,得到四边形A4B4C4D4,它与四边形A3B3C3D3相比有什么变化?
3
解:将四边形A3B3C3D3向下平移4个单位长度,得到四
边形A4B4C4D4 ,形状、大小未发生变化.
典题精讲
在平面直角坐标系中,将三角形各点的纵坐标都减4,横坐标保持不变,所得图形与原图形相比,( )
A.向右平移了4个单位长度
B.向左平移了4个单位长度
C.向上平移了4个单位长度
D.向下平移了4个单位长度
4
D
典题精讲
如图,在平面直角坐标系中,将点M (2,1)向下平移2个单位长度得到点N,则点N 的坐标为( )
A.(2,-1)
B.(2,3)
C.(0,1)
D.(4,1)
5
A
典题精讲
6
若一个四边形上的其中一点P 在平移的过程中,坐标变化为P (x,y ) →P ′(x+3,y ),则该四边形的平移情况是( )
A.向左平移3个单位长度
B.向右平移3个单位长度
C.向上平移3个单位长度
D.向下平移3个单位长度
C
典题精讲
7
如图,与图①中的三角形相比,图②中的三角形发生的变化是( )
A.向左平移了3个单位长度
B.向右平移了1个单位长度
C.向上平移了3个单位长度
D.向下平移了1个单位长度
A
典题精讲
8
如图,△ABO 的顶点B 的坐标是(-2,0),将△ABO 沿 y 轴向上平移3个单位长度后,点B 的对应点的坐标是_____________.
(-2,3)
易错提醒
如图,△OAB 的顶点A 的坐标为(3,5),点B (4,0),把△OAB 沿x 轴向右平移得到
△CDE,如果CB=1,那么点
D 的坐标为________.
易错点:忽视平移性质中所有对应点的平移方向、
距离的关系而致错
(6,5)
易错提醒
∵点B (4,0),CB=1,∴OC=3.
∴△OAB 平移的距离为3.
∴点D 是由点A 向右平移3个单位长度得到的.
∴D 的坐标为(6,5).
本题易错之处在于忽视图形平移过程中所有对应点的平移方向、平移距离是一致的.
学以致用
小试牛刀
已知点A (-2,-1),将点A 沿x 轴方向平移2个单位长度得到点B,则点B 的坐标为( )
A.(-4,-1)
B.(0,-1)
C.(-4,-1)或(0,-1)
D.以上都不对
1
C
小试牛刀
如图,在平面直角坐标系中,△ABC 位于第二象限,点A 的坐标是(-2,3),先把△ABC 向右平移4个单位长度得到△A1B1C1,再作与△A1B1C1关于x 轴对称的△A2B2C2,则点A 的对应点A2的坐标是( )
A.(-3,2)
B.(2,-3)
C.(1,-2)
D.(-1,2)
2
B
小试牛刀
3
如图,将直线 y=-x 沿y 轴向下平移后的直线恰好经过点A (2,-4),且与y 轴交于点B,在x 轴上存在一点P
使得PA+PB 的值最小,则点
P 的坐标为________.
小试牛刀
4 如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P1.
(1)画出⊙P1;
(2)设⊙P1与x 轴正半轴,y 轴正半轴
的交点分别为A,B,求劣弧AB 与
弦AB 围成的图形的面积(结果保留π).
小试牛刀
(1)如图,⊙P1即为所求.
(2)如图,劣弧AB 与弦AB 围成的图形的面积为
解:
小试牛刀
5 在如图所示的直角坐标系中,解答下列问题:
(1)已知A (2,0),B (-1,-4),C (3,-3)三点,分别在坐标系中找出它们,并连接得到三角形ABC;
(2)将三角形ABC 向上平移4个单位长度,得到三角形A1B1C1;
(3)求三角形A1B1C1的面积.
小试牛刀
(1)如图.
(2)如图.
(3)三角形A1B1C1的面积为
4×4- ×4×1- ×1×3- ×3×4=6.5.
解:
小试牛刀
6 如图,点P (2a-12,1-a )位于第三象限,点Q (x,y )位于第二象限且是由点P 向上平移一定单位长度得到的.
(1)若点P 的纵坐标为-3,试求出a 的值;
(2)在(1)的条件下,试求出符合条件的一个Q 的坐标;
(3)若点P 的横、纵坐标都是整数,试求出a 的值以及线段PQ 长度的取值范围.
小试牛刀
(1)1-a=-3,a=4.
(2)由a=4得2a-12=2×4-12=-4.
又点Q (x,y )位于第二象限,所以y>0.
取y=1,得点Q 的坐标为(-4,1)
(答案不唯一,其他符合题意也可).
(3)因为点P (2a-12,1-a )位于第三象限,
所以
解得1<a<6.
解:
小试牛刀
因为点P 的横、纵坐标都是整数,
所以a=2 或 3或 4 或 5.
当a=2时,1-a=-1,
所以PQ>1;
当a=3时,1-a=-2,所以PQ>2;
当a=4时,1-a=-3,所以PQ>3;
当a=5时,1-a=-4,所以PQ>4.
小试牛刀
如图,在平面直角坐标系中,点A,B 在x 轴上,且A (-10,0),
AB=4,△ABC 的面积为14.将△ABC 沿x 轴向右平移得到△DEF,
当点D 为AB 中点时,点F 恰好在 y 轴上.求:
(1)点F 的坐标;
(2)△EOF 的面积.
小试牛刀
(1)∵A (-10,0),AB=4,
∴B (-6,0).
∵S△ABC= AB | yc |=14,
∴| yc |=7.
∵点C 在第二象限,∴yc=7.
∵△ABC 沿x 轴向右平移得到△DEF,点F 在 y 轴上,
∴F (0,7).
解:
小试牛刀
(2)∵A (-10,0),B (-6,0),D 为AB 中点,
∴D (-8,0).
∵DE=AB=4,
∴E (-4,0).∴OE=4.
∴S△EOF= OE OF= ×4×7=14.
课堂小结
课堂小结
点的平移与点的坐标变化规律:
左、右平移,横变纵不变,“右加左减”;
上、下平移,纵变横不变,“上加下减”.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
