【班海精品】北师大版(新)八年级下-3.2图形的旋转 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-3.2图形的旋转 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览








文档简介
(共40张PPT)
2.图形的旋转
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
◆旋转前、后的图形 .
◆对应点到旋转中心的距离 .
◆对应点与旋转中心所连线段的夹角等于 .
◆图形的旋转是由 和旋转的决定.
相等
旋转角
全等
旋转中心
复习回顾
旋转的基本性质:
新课精讲
探索新知
1
知识点
旋转作图
作图工具:尺、规、笔.
基本作图技能:
作一条直线平行于已知直线;
作一线段等于已知线段;
作一角等于已知角.
回顾已经学过的尺规作图
探索新知
简单的旋转作图:
旋转中心,用点表示;旋转方向分为顺时针方向和逆时针方向.
角度,用量角器度量,或通过画角度等于已知角.
简单旋转作图的一般步骤:
(1)找出图形的关键点;
(2)确定旋转中心、旋转方向和旋转角;
(3)将关键点与旋转中心连接起来,然后按旋转方向分别将它们旋转一个角度,得到关键点的对应点;
(4)按照原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
探索新知
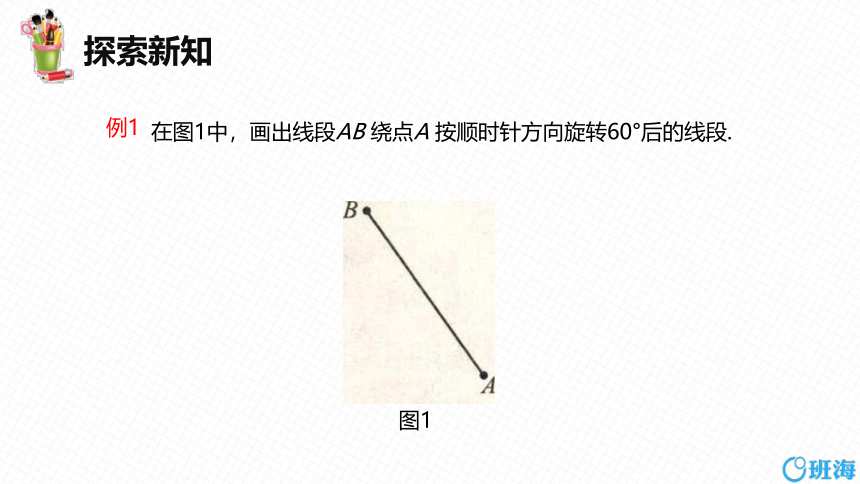
在图1中,画出线段AB 绕点A 按顺时针方向旋转60°后的线段.
例1
图1
探索新知
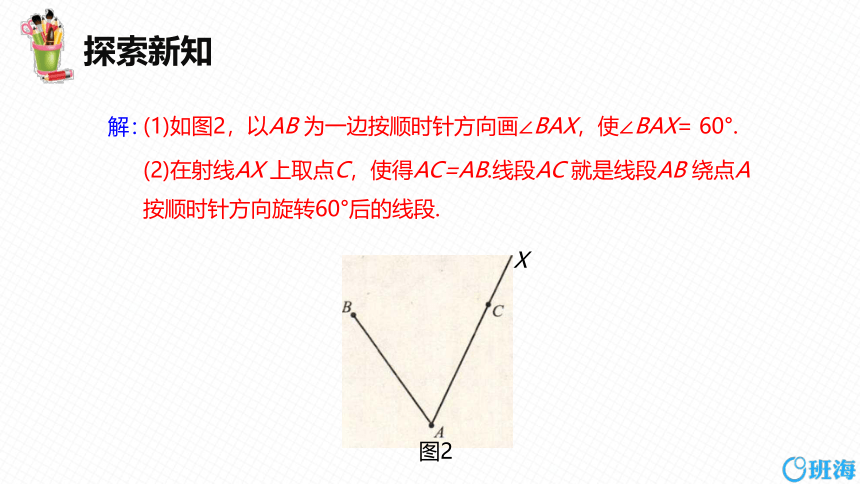
解:
(1)如图2,以AB 为一边按顺时针方向画∠BAX,使∠BAX= 60°.
(2)在射线AX 上取点C,使得AC=AB.线段AC 就是线段AB 绕点A 按顺时针方向旋转60°后的线段.
图2
X
探索新知
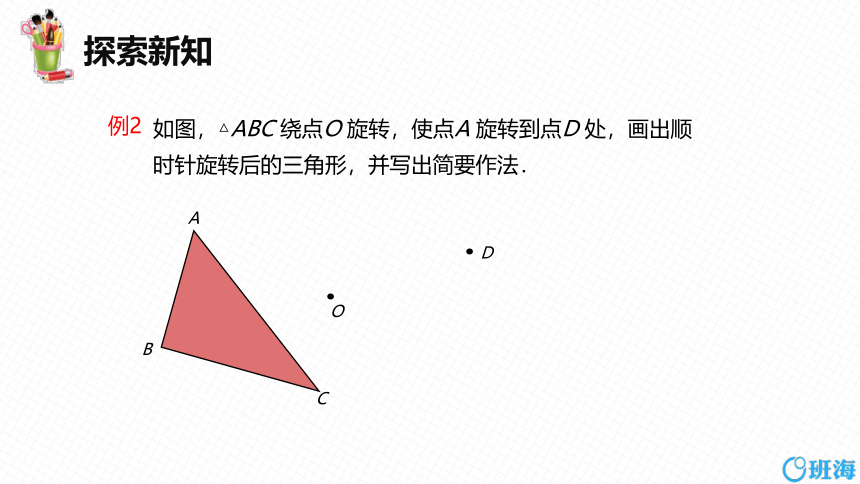
如图,△ABC 绕点O 旋转,使点A 旋转到点D 处,画出顺时针旋转后的三角形,并写出简要作法.
例2
A
B
C
.
.
O
D
探索新知
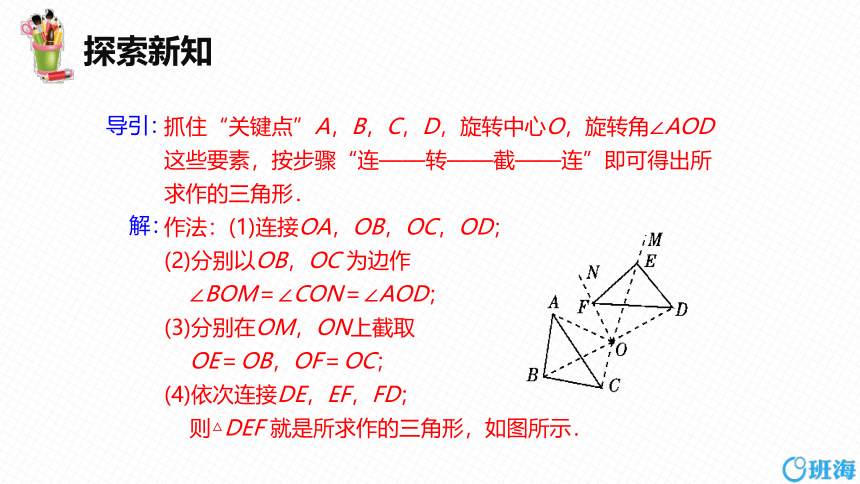
抓住“关键点”A,B,C,D,旋转中心O,旋转角∠AOD这些要素,按步骤“连——转——截——连”即可得出所求作的三角形.
作法:(1)连接OA,OB,OC,OD;
(2)分别以OB,OC 为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF 就是所求作的三角形,如图所示.
导引:
解:
探索新知
总 结
在旋转作图时,要紧扣以下三点:
(1)对应点到旋转中心的距离相等;
(2)旋转的角度相等;
(3)旋转的方向相同.
探索新知
如图,在方格纸上,△DEF 是由△ABC 绕定点P 顺时针旋转得到的,如果用(2,1)表示方格纸上A 点的位置,(1,2)表示B 点的位置,那么点P 的位置为( )
A.(5,2)
B.(2,5)
C.(2,1)
D.(1,2)
例3
A
探索新知
如图,分别连接AD,CF,然后作它们的垂直平分线,相交于P 点,则旋转中心为P,易得点P 的坐标为(5,2).
导引:
探索新知
总 结
确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若不在图形上,对应点连线的垂直平分线的交点就是旋转中心,旋转角等于对应点与旋转中心所连线段的夹角.
典题精讲
在图中画出线段AB 绕点O 按顺时针方向旋转50°后的线段.
如图,过O 在AB 右侧作∠AOF=50°,在OF上截取OC=OA,延长FO,在FO 的延长线上截取OD=OB,线段CD 就是线段AB 绕点O 按顺时针方向旋转50°后的线段.
解:
典题精讲
将如图所示的五边形绕点O按顺时针方向旋转90°,画出旋转后的图形.
过点O 分别作各个顶点与点O 连线的垂线,并在每条垂线上截取与相应线段相等的线段,得到各个顶点绕O 点按顺时针方向旋转90°后的对应点,然后按原来的方式连接相应的顶点即可得到旋转后的图形(如图).
解:
典题精讲
如图,将线段AB 绕点O 顺时针旋转90°得到线段A′B ′,
那么点A(-2,5)的对应点A′的坐标是________.
(5,2)
探索新知
2
知识点
用旋转变换设计图案
问 题
让我们一起来欣赏一下美丽的图案,体会一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
探索新知
O
O
β
α
(1)旋转中心不变,改变旋转角(如图).
探索新知
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
探索新知
(3)美丽的图案是这样形成的.
探索新知
归 纳
我们可以利用旋转中心不变,改变旋转角;旋转角不变,改变旋转中心设计许多美丽的图案.
探索新知
例4 如图(1)是某一种花的花瓣和中心,现以 O 为旋转中心画出
分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的
这种花的图形.
解:如图(2).
O
O
图(1)
图(2)
探索新知
总 结
本题是将基本图形按旋转图形的作法,分别按七个角度作旋转图形.作旋转图形时注意旋转三要素:旋转中心、旋转方向、旋转角.
探索新知
同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG 可以看成是四边形ABCD 以A为旋转中心( )
A.顺时针旋转60°得到的
B.顺时针旋转120°得到的
C.逆时针旋转60°得到的
D.逆时针旋转120°得到的
B
例5
典题精讲
1 如图所示的4个图案,能通过基本图形旋转得到的有( )
A.1个 B.2个 C.3个 D.4个
D
典题精讲
如图是甲、乙两张不同的纸片,将它们分别沿着虚线剪开后,
各自要拼一个与原来面积相等的正方形,则( )
A.甲、乙都可以 B.甲、乙都不可以
C.甲不可以,乙可以 D.甲可以,乙不可以
A
学以致用
小试牛刀
1 如图,在4×4的正方形网格中,△MNP 绕某点旋转一定的角度,
得到△M1N1P1,则其旋转中心是( )
A.点A B.点B C.点C D.点D
B
小试牛刀
2
如图,在正方形网格中,线段A′B ′是线段AB 绕某点逆时针旋转角α 得到的,点A′ 与A对应,则角α 的大小为( )
A.30°
B.60°
C.90°
D.120°
C
小试牛刀
3 在4×4的方格纸中,△ABC 的三个顶点都在格点上.
(1)在图①中画出与△ABC 成轴对称且与△ABC 有公共边的格点三角形(画出一个即可);
(2)将图②中的△ABC 绕着点C 按顺时针方向旋转90°,画出旋转后的三角形.
小试牛刀
(1)如图①,△A′BC 即为所求,答案不唯一.
(2)如图②,△A′B ′C 即为所求.
解:
小试牛刀
4 如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别为A (-3,4),B (-5,2),C (-2,1).
(1)画出△ABC 关于y 轴的对称图形△A1B1C1;
(2)画出将△ABC 绕原点O 逆时针方向旋转90°得到的△A2B2C2;
(3)求(2)中线段OA 扫过的图形面积.
小试牛刀
(1)根据关于y 轴对称的点纵坐标相同,横坐标互为相反数的特点,得出A1(3,4),B1(5,2),C1(2,1),△ABC 关于y 轴的对称图形△A1B1C1如图所示.
解:
小试牛刀
(2)根据绕原点O 逆时针旋转90°的点的坐标特点:横坐标为原纵坐标的相反数,纵坐标为原横坐标,可知,△A2B2C2各顶点的坐标分别为A2(-4,-3),B2(-2,-5),C2(-1,-2),如图所示.
小试牛刀
(3)如图,(2)中线段OA 扫过的图形面积是扇形AOA2的面积,即阴影部分的面积,
∵A(-3,4),
∴AO=
∵旋转角∠AOA2=90°,
∴扇形AOA2的面积为 ×π×52= π.
课堂小结
课堂小结
旋转作图的一般步骤:
一连:连接已知点与旋转中心;
二定:确定旋转方向;
三量:测量旋转角度;
四截:在旋转角的另一条边上以旋转中心为一端点截
取等于对应线段长度的线段;
五画:顺次连接所得的点,从而画出旋转得到的图形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.图形的旋转
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
◆旋转前、后的图形 .
◆对应点到旋转中心的距离 .
◆对应点与旋转中心所连线段的夹角等于 .
◆图形的旋转是由 和旋转的决定.
相等
旋转角
全等
旋转中心
复习回顾
旋转的基本性质:
新课精讲
探索新知
1
知识点
旋转作图
作图工具:尺、规、笔.
基本作图技能:
作一条直线平行于已知直线;
作一线段等于已知线段;
作一角等于已知角.
回顾已经学过的尺规作图
探索新知
简单的旋转作图:
旋转中心,用点表示;旋转方向分为顺时针方向和逆时针方向.
角度,用量角器度量,或通过画角度等于已知角.
简单旋转作图的一般步骤:
(1)找出图形的关键点;
(2)确定旋转中心、旋转方向和旋转角;
(3)将关键点与旋转中心连接起来,然后按旋转方向分别将它们旋转一个角度,得到关键点的对应点;
(4)按照原图形的顺序连接这些对应点,所得到的图形就是旋转后的图形.
探索新知
在图1中,画出线段AB 绕点A 按顺时针方向旋转60°后的线段.
例1
图1
探索新知
解:
(1)如图2,以AB 为一边按顺时针方向画∠BAX,使∠BAX= 60°.
(2)在射线AX 上取点C,使得AC=AB.线段AC 就是线段AB 绕点A 按顺时针方向旋转60°后的线段.
图2
X
探索新知
如图,△ABC 绕点O 旋转,使点A 旋转到点D 处,画出顺时针旋转后的三角形,并写出简要作法.
例2
A
B
C
.
.
O
D
探索新知
抓住“关键点”A,B,C,D,旋转中心O,旋转角∠AOD这些要素,按步骤“连——转——截——连”即可得出所求作的三角形.
作法:(1)连接OA,OB,OC,OD;
(2)分别以OB,OC 为边作
∠BOM=∠CON=∠AOD;
(3)分别在OM,ON上截取
OE=OB,OF=OC;
(4)依次连接DE,EF,FD;
则△DEF 就是所求作的三角形,如图所示.
导引:
解:
探索新知
总 结
在旋转作图时,要紧扣以下三点:
(1)对应点到旋转中心的距离相等;
(2)旋转的角度相等;
(3)旋转的方向相同.
探索新知
如图,在方格纸上,△DEF 是由△ABC 绕定点P 顺时针旋转得到的,如果用(2,1)表示方格纸上A 点的位置,(1,2)表示B 点的位置,那么点P 的位置为( )
A.(5,2)
B.(2,5)
C.(2,1)
D.(1,2)
例3
A
探索新知
如图,分别连接AD,CF,然后作它们的垂直平分线,相交于P 点,则旋转中心为P,易得点P 的坐标为(5,2).
导引:
探索新知
总 结
确定旋转中心与旋转角的方法:
在图形的旋转过程中,判断谁是旋转中心,要看旋转中心是在图形上还是不在图形上;若在图形上,哪一点在旋转过程中位置没有改变,这一点就是旋转中心;若不在图形上,对应点连线的垂直平分线的交点就是旋转中心,旋转角等于对应点与旋转中心所连线段的夹角.
典题精讲
在图中画出线段AB 绕点O 按顺时针方向旋转50°后的线段.
如图,过O 在AB 右侧作∠AOF=50°,在OF上截取OC=OA,延长FO,在FO 的延长线上截取OD=OB,线段CD 就是线段AB 绕点O 按顺时针方向旋转50°后的线段.
解:
典题精讲
将如图所示的五边形绕点O按顺时针方向旋转90°,画出旋转后的图形.
过点O 分别作各个顶点与点O 连线的垂线,并在每条垂线上截取与相应线段相等的线段,得到各个顶点绕O 点按顺时针方向旋转90°后的对应点,然后按原来的方式连接相应的顶点即可得到旋转后的图形(如图).
解:
典题精讲
如图,将线段AB 绕点O 顺时针旋转90°得到线段A′B ′,
那么点A(-2,5)的对应点A′的坐标是________.
(5,2)
探索新知
2
知识点
用旋转变换设计图案
问 题
让我们一起来欣赏一下美丽的图案,体会一下旋转的奥秘.你们猜猜旋转到底和什么有关呢?
探索新知
O
O
β
α
(1)旋转中心不变,改变旋转角(如图).
探索新知
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
探索新知
(3)美丽的图案是这样形成的.
探索新知
归 纳
我们可以利用旋转中心不变,改变旋转角;旋转角不变,改变旋转中心设计许多美丽的图案.
探索新知
例4 如图(1)是某一种花的花瓣和中心,现以 O 为旋转中心画出
分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的
这种花的图形.
解:如图(2).
O
O
图(1)
图(2)
探索新知
总 结
本题是将基本图形按旋转图形的作法,分别按七个角度作旋转图形.作旋转图形时注意旋转三要素:旋转中心、旋转方向、旋转角.
探索新知
同学们曾玩过万花筒,它是由三块等宽等长的玻璃片围成的.如图是在万花筒中看到的一个图案.图中所有小三角形均是全等的等边三角形,其中的四边形AEFG 可以看成是四边形ABCD 以A为旋转中心( )
A.顺时针旋转60°得到的
B.顺时针旋转120°得到的
C.逆时针旋转60°得到的
D.逆时针旋转120°得到的
B
例5
典题精讲
1 如图所示的4个图案,能通过基本图形旋转得到的有( )
A.1个 B.2个 C.3个 D.4个
D
典题精讲
如图是甲、乙两张不同的纸片,将它们分别沿着虚线剪开后,
各自要拼一个与原来面积相等的正方形,则( )
A.甲、乙都可以 B.甲、乙都不可以
C.甲不可以,乙可以 D.甲可以,乙不可以
A
学以致用
小试牛刀
1 如图,在4×4的正方形网格中,△MNP 绕某点旋转一定的角度,
得到△M1N1P1,则其旋转中心是( )
A.点A B.点B C.点C D.点D
B
小试牛刀
2
如图,在正方形网格中,线段A′B ′是线段AB 绕某点逆时针旋转角α 得到的,点A′ 与A对应,则角α 的大小为( )
A.30°
B.60°
C.90°
D.120°
C
小试牛刀
3 在4×4的方格纸中,△ABC 的三个顶点都在格点上.
(1)在图①中画出与△ABC 成轴对称且与△ABC 有公共边的格点三角形(画出一个即可);
(2)将图②中的△ABC 绕着点C 按顺时针方向旋转90°,画出旋转后的三角形.
小试牛刀
(1)如图①,△A′BC 即为所求,答案不唯一.
(2)如图②,△A′B ′C 即为所求.
解:
小试牛刀
4 如图,在平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC 的三个顶点的坐标分别为A (-3,4),B (-5,2),C (-2,1).
(1)画出△ABC 关于y 轴的对称图形△A1B1C1;
(2)画出将△ABC 绕原点O 逆时针方向旋转90°得到的△A2B2C2;
(3)求(2)中线段OA 扫过的图形面积.
小试牛刀
(1)根据关于y 轴对称的点纵坐标相同,横坐标互为相反数的特点,得出A1(3,4),B1(5,2),C1(2,1),△ABC 关于y 轴的对称图形△A1B1C1如图所示.
解:
小试牛刀
(2)根据绕原点O 逆时针旋转90°的点的坐标特点:横坐标为原纵坐标的相反数,纵坐标为原横坐标,可知,△A2B2C2各顶点的坐标分别为A2(-4,-3),B2(-2,-5),C2(-1,-2),如图所示.
小试牛刀
(3)如图,(2)中线段OA 扫过的图形面积是扇形AOA2的面积,即阴影部分的面积,
∵A(-3,4),
∴AO=
∵旋转角∠AOA2=90°,
∴扇形AOA2的面积为 ×π×52= π.
课堂小结
课堂小结
旋转作图的一般步骤:
一连:连接已知点与旋转中心;
二定:确定旋转方向;
三量:测量旋转角度;
四截:在旋转角的另一条边上以旋转中心为一端点截
取等于对应线段长度的线段;
五画:顺次连接所得的点,从而画出旋转得到的图形.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
