【班海精品】北师大版(新)八年级下-5.3分式的加减法 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-5.3分式的加减法 第四课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览






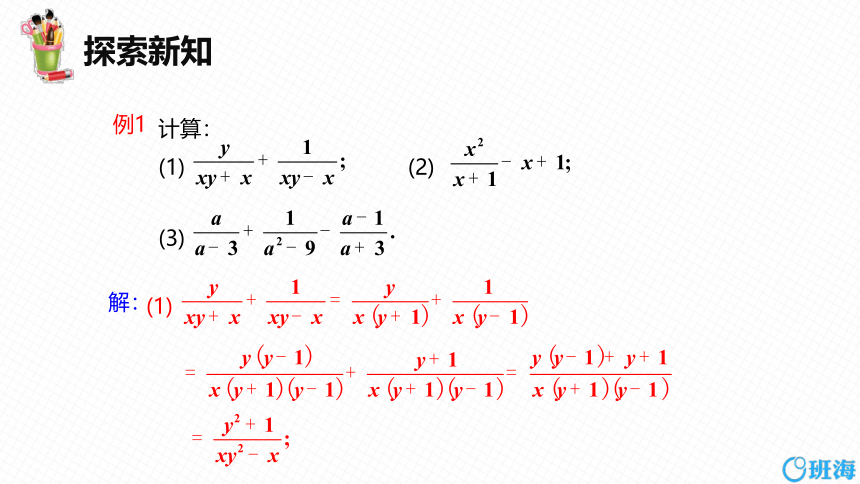
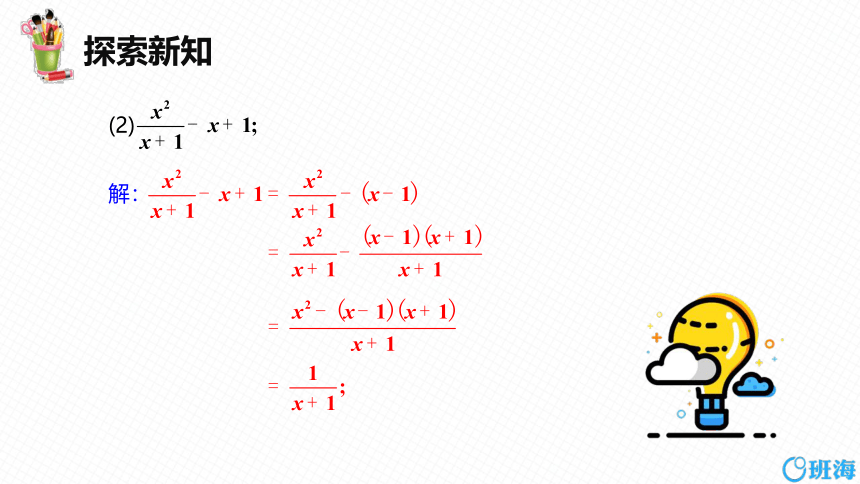


文档简介
(共46张PPT)
3.分式的加减法
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
1. 只含某一级运算:从左到右依次运算.
2. 有不同级运算在一起的:从高级到低级运算先算
乘方三级;再算乘除二级;最后算加减一级.
3. 带有括号的运算:从内到外依次进行运算先算小
括号;再算中括号;最后算大括号里面的.
有理数和整式的混合运算法则:
新课精讲
探索新知
1
知识点
分式的混合运算
分式的加、减、乘、除、乘方的混合运算顺序原则:
优先进行乘方运算,其次进行乘、除运算,最后进行加、减运算;如果有括号,则优先进行括号内的运算.
对于同级运算,则按照从左到右的顺序,依次进行.
探索新知
计算:
(1) (2)
(3)
例1
(1)
解:
探索新知
(2)
解:
探索新知
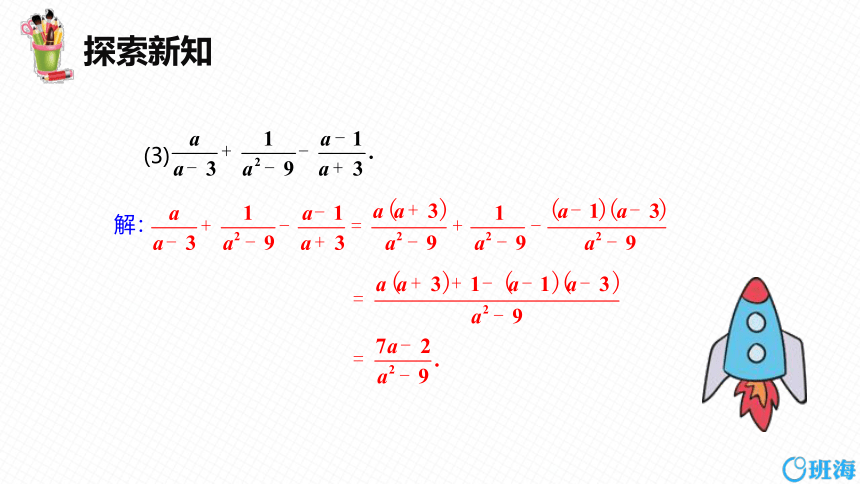
(3)
解:
探索新知
先化简,再求值:
其中,a 满足a-2=0.
例2
原式括号中两项通分并利用同分母分式的加法法则
计算,同时利用除法法则变形,约分得到最简结果,
将a 的值代入计算即可求出值.
导引:
探索新知
解:
原式
当a-2=0,即a=2时,原式=3.
探索新知
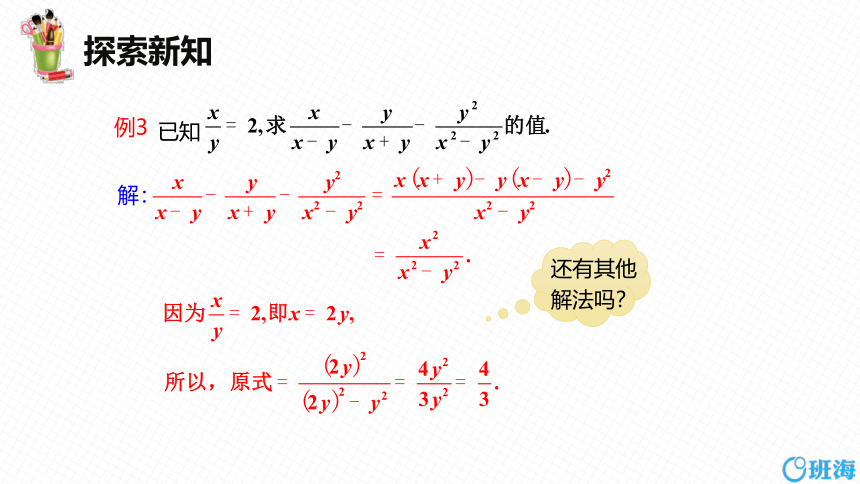
已知
例3
解:
还有其他解法吗?
典题精讲
1
计算:
解:
典题精讲
解:
典题精讲
2
下列等式成立的是( )
B.
C. D.
C
计算 的结果是( )
A.-4 B.4
C.2a D.-2a
3
A
典题精讲
化简 的结果为( )
A. B.
C. D.
4
A
化简 的结果是( )
A. B.
C.x+1 D.x-1
5
A
探索新知
2
知识点
分式混合运算的应用
做一做
根据规划设计,某工程队准备修建一条长1120 m的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10 m,从而缩短了工期.假设原计划每天修建盲道x cm,那么
(1)原计划修建这条盲道需要多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?
探索新知
甲、乙两位采购员同去一家饲料公司购买两次饲料.
两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1 000 kg,乙每次用去800元.
(1)甲、乙两次所购饲料的平均价格各是多少?
(2)谁的购货方式更合算?
例4
探索新知
(1)设两次购买的饲料价格分别为m 元/kg和n 元/kg
(m,n 是正数,且m≠n).
甲两次所购饲料的平均价格为
乙两次所购饲料的平均价格为
解:
探索新知
(2)
因为m,n 都是正数,且m≠n,
所以 也是正数.
即
因此乙的购货方式更合算.
解:
(2)谁的购货方式更合算?
典题精讲
1
先化简,再求值:
(1)当a= 时,求 的值;
(2)设x=3y,求 的值
解:
当a= 时,原式=
典题精讲
当x=3y 时,原式=
典题精讲
2 若 则W=( )
A.a+2(a≠-2) B.-a+2(a≠2)
C.a-2(a≠2) D.-a-2(a≠±2)
3 已知实数a,b,c 满足a+b=ab=c,有下列结论:
①若c≠0,则 ②若a=3,则b+c=9;
③若a=b=c,则abc=0;
④若a,b,c 中只有两个数相等,则a+b+c=8.
其中正确的是_____________(填正确结论的序号).
D
①③④
典题精讲
3 一个批发兼零售的文具店规定:凡一次购买铅笔301支以上(包括301支)可按批发价付款;购买300支以下(包括300支)只能按零售价付款.现有学生小明购买铅笔,如果给九年级学生每人买1支,那么只能按零售价付款,需用(m 2-1)元;如果多买60支,那么可按批发价付款,同样需用(m 2-1)元.设九年级共有x 名学生,解答下列问题:
(1)求x 的取值范围.
(2)每支铅笔的零售价、批发价分别为多少元?(用含x,m 的式子表示)
(3)每支铅笔的零售价比批发价贵多少元?
典题精讲
解:
(1)由题意可得
解得241≤x≤300.
故x 的取值范围是241≤x≤300,且x 为正整数.
(2)每支铅笔的零售价为 元,
每支铅笔的批发价为 元.
典题精讲
∴每支铅笔的零售价比批发价贵 元.
易错提醒
1.计算:
易错点:在进行分式的混合运算时运算顺序出错
解:
易错提醒
易错总结:
乘、除是同级运算,应该按照从左到右的顺序进行,本题由于后两个分式互为倒数,容易错解为
实际上是运算顺序错了.
易错提醒
2.计算:
易错点:在进行分式的混合运算时,错用运算律或计算不彻底造成错误
解:
易错提醒
易错总结:
本题易误以为除法有分配律,而错解为
学以致用
小试牛刀
计算: =________.
计算: =________.
1
2
a-b
0
小试牛刀
先化简:
然后解答下列问题:
(1)当x=3时,求式子的值;
(2)原式的值能等于-1吗?为什么?
小试牛刀
解:
小试牛刀
(1)当x=3时,原式=
(2)不能.如果 那么x+1=-(x-1),
解得x=0,当x=0时,除式 原式无意义,故原式的值不能等于-1.
小试牛刀
4 先化简,再求值:
解:
原式
小试牛刀
解不等式组
∴不等式组的整数解有-1,0,1,2.
∵分式有意义时x ≠±1,0,
∴x=2.
当x=2时,原式=
小试牛刀
5 先化简,再求值:
解:
小试牛刀
6 计算:
解:
原式
小试牛刀
7 计算:
解:
原式
小试牛刀
8
小试牛刀
解:
小试牛刀
9
原式
因为x 为正整数,且 也为正整数,所以x-3=1
或x-3=2.解得x=4或x=5.
解:
课堂小结
课堂小结
1.分式混合运算的步骤:
先乘方,再乘除,最后加减,有括号先算括号里面的.
2.分式混合运算常出现的错误:
(1)运算顺序易错;
(2)符号变换易错;
(3)错用分配律,只有乘法才有分配律;
(4)忽视分数线的括号作用;
(5)运算的结果不是最简分式或整式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.分式的加减法
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
回顾旧知
1. 只含某一级运算:从左到右依次运算.
2. 有不同级运算在一起的:从高级到低级运算先算
乘方三级;再算乘除二级;最后算加减一级.
3. 带有括号的运算:从内到外依次进行运算先算小
括号;再算中括号;最后算大括号里面的.
有理数和整式的混合运算法则:
新课精讲
探索新知
1
知识点
分式的混合运算
分式的加、减、乘、除、乘方的混合运算顺序原则:
优先进行乘方运算,其次进行乘、除运算,最后进行加、减运算;如果有括号,则优先进行括号内的运算.
对于同级运算,则按照从左到右的顺序,依次进行.
探索新知
计算:
(1) (2)
(3)
例1
(1)
解:
探索新知
(2)
解:
探索新知
(3)
解:
探索新知
先化简,再求值:
其中,a 满足a-2=0.
例2
原式括号中两项通分并利用同分母分式的加法法则
计算,同时利用除法法则变形,约分得到最简结果,
将a 的值代入计算即可求出值.
导引:
探索新知
解:
原式
当a-2=0,即a=2时,原式=3.
探索新知
已知
例3
解:
还有其他解法吗?
典题精讲
1
计算:
解:
典题精讲
解:
典题精讲
2
下列等式成立的是( )
B.
C. D.
C
计算 的结果是( )
A.-4 B.4
C.2a D.-2a
3
A
典题精讲
化简 的结果为( )
A. B.
C. D.
4
A
化简 的结果是( )
A. B.
C.x+1 D.x-1
5
A
探索新知
2
知识点
分式混合运算的应用
做一做
根据规划设计,某工程队准备修建一条长1120 m的盲道.由于采用新的施工方式,实际每天修建盲道的长度比原计划增加10 m,从而缩短了工期.假设原计划每天修建盲道x cm,那么
(1)原计划修建这条盲道需要多少天?实际修建这条盲道用了多少天?
(2)实际修建这条盲道的工期比原计划缩短了几天?
探索新知
甲、乙两位采购员同去一家饲料公司购买两次饲料.
两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1 000 kg,乙每次用去800元.
(1)甲、乙两次所购饲料的平均价格各是多少?
(2)谁的购货方式更合算?
例4
探索新知
(1)设两次购买的饲料价格分别为m 元/kg和n 元/kg
(m,n 是正数,且m≠n).
甲两次所购饲料的平均价格为
乙两次所购饲料的平均价格为
解:
探索新知
(2)
因为m,n 都是正数,且m≠n,
所以 也是正数.
即
因此乙的购货方式更合算.
解:
(2)谁的购货方式更合算?
典题精讲
1
先化简,再求值:
(1)当a= 时,求 的值;
(2)设x=3y,求 的值
解:
当a= 时,原式=
典题精讲
当x=3y 时,原式=
典题精讲
2 若 则W=( )
A.a+2(a≠-2) B.-a+2(a≠2)
C.a-2(a≠2) D.-a-2(a≠±2)
3 已知实数a,b,c 满足a+b=ab=c,有下列结论:
①若c≠0,则 ②若a=3,则b+c=9;
③若a=b=c,则abc=0;
④若a,b,c 中只有两个数相等,则a+b+c=8.
其中正确的是_____________(填正确结论的序号).
D
①③④
典题精讲
3 一个批发兼零售的文具店规定:凡一次购买铅笔301支以上(包括301支)可按批发价付款;购买300支以下(包括300支)只能按零售价付款.现有学生小明购买铅笔,如果给九年级学生每人买1支,那么只能按零售价付款,需用(m 2-1)元;如果多买60支,那么可按批发价付款,同样需用(m 2-1)元.设九年级共有x 名学生,解答下列问题:
(1)求x 的取值范围.
(2)每支铅笔的零售价、批发价分别为多少元?(用含x,m 的式子表示)
(3)每支铅笔的零售价比批发价贵多少元?
典题精讲
解:
(1)由题意可得
解得241≤x≤300.
故x 的取值范围是241≤x≤300,且x 为正整数.
(2)每支铅笔的零售价为 元,
每支铅笔的批发价为 元.
典题精讲
∴每支铅笔的零售价比批发价贵 元.
易错提醒
1.计算:
易错点:在进行分式的混合运算时运算顺序出错
解:
易错提醒
易错总结:
乘、除是同级运算,应该按照从左到右的顺序进行,本题由于后两个分式互为倒数,容易错解为
实际上是运算顺序错了.
易错提醒
2.计算:
易错点:在进行分式的混合运算时,错用运算律或计算不彻底造成错误
解:
易错提醒
易错总结:
本题易误以为除法有分配律,而错解为
学以致用
小试牛刀
计算: =________.
计算: =________.
1
2
a-b
0
小试牛刀
先化简:
然后解答下列问题:
(1)当x=3时,求式子的值;
(2)原式的值能等于-1吗?为什么?
小试牛刀
解:
小试牛刀
(1)当x=3时,原式=
(2)不能.如果 那么x+1=-(x-1),
解得x=0,当x=0时,除式 原式无意义,故原式的值不能等于-1.
小试牛刀
4 先化简,再求值:
解:
原式
小试牛刀
解不等式组
∴不等式组的整数解有-1,0,1,2.
∵分式有意义时x ≠±1,0,
∴x=2.
当x=2时,原式=
小试牛刀
5 先化简,再求值:
解:
小试牛刀
6 计算:
解:
原式
小试牛刀
7 计算:
解:
原式
小试牛刀
8
小试牛刀
解:
小试牛刀
9
原式
因为x 为正整数,且 也为正整数,所以x-3=1
或x-3=2.解得x=4或x=5.
解:
课堂小结
课堂小结
1.分式混合运算的步骤:
先乘方,再乘除,最后加减,有括号先算括号里面的.
2.分式混合运算常出现的错误:
(1)运算顺序易错;
(2)符号变换易错;
(3)错用分配律,只有乘法才有分配律;
(4)忽视分数线的括号作用;
(5)运算的结果不是最简分式或整式.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
