【班海精品】北师大版(新)八年级下-6.1平行四边形的性质 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)八年级下-6.1平行四边形的性质 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:28 | ||
图片预览








文档简介
(共44张PPT)
1.平行四边形的性质
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平行四边形的性质:
对边相等;
对角相等
回顾旧知
新课精讲
探索新知
1
知识点
平行四边形的性质——对角线互相平分
在上一课的“做一做”中,我们还发现:平行四边形的对角线互相平分. 请你尝试证明这一结论.
探索新知
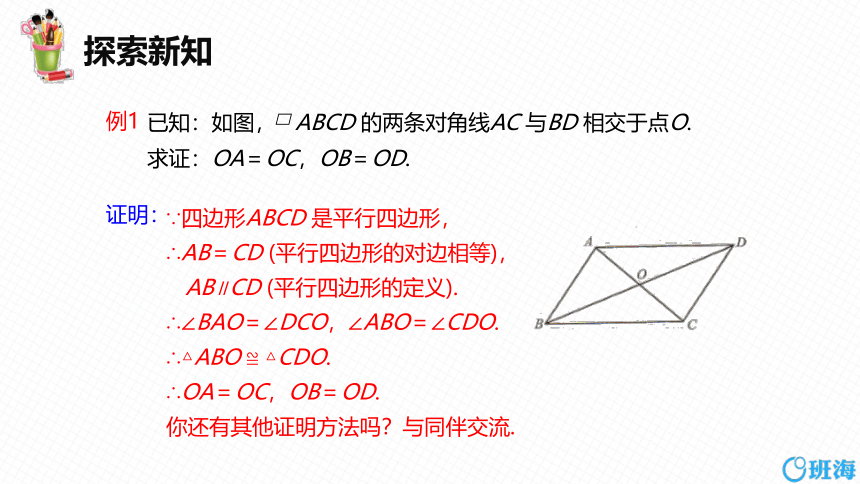
已知:如图, ABCD 的两条对角线AC 与BD 相交于点O.求证:OA=OC,OB=OD.
∵四边形ABCD 是平行四边形,
∴AB=CD (平行四边形的对边相等),
AB∥CD (平行四边形的定义).
∴∠BAO=∠DCO,∠ABO=∠CDO.
∴△ABO ≌ △CDO.
∴OA=OC,OB=OD.
你还有其他证明方法吗?与同伴交流.
证明:
例1
探索新知
定理 平行四边形的对角线互相平分.
总 结
探索新知
对角线的性质:平行四边形的对角线互相平分.
数学表达式:
如图,∵四边形ABCD 是平行四边形,
对角线AC,BD 相交于点O,
∴OA=OC,OB=OD.
探索新知
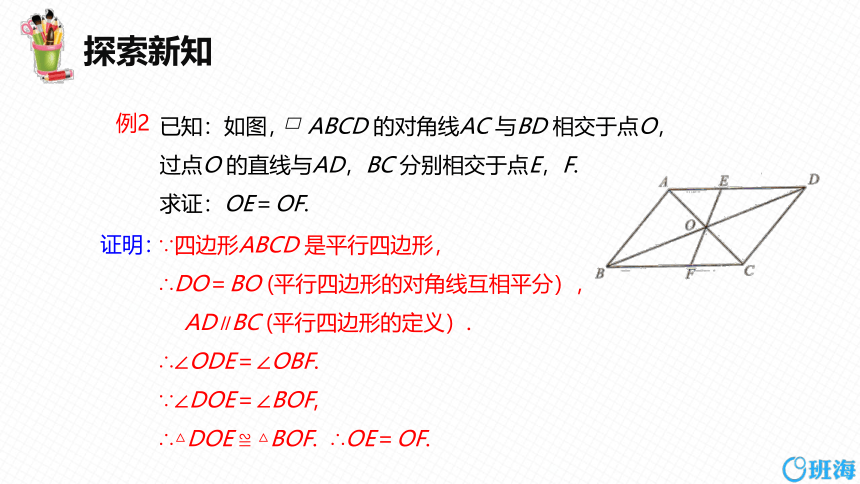
例2
证明:
∵四边形ABCD 是平行四边形,
∴DO=BO (平行四边形的对角线互相平分),
AD∥BC (平行四边形的定义).
∴∠ODE=∠OBF.
∵∠DOE=∠BOF,
∴△DOE ≌ △BOF. ∴OE=OF.
已知:如图, ABCD 的对角线AC 与BD 相交于点O,
过点O 的直线与AD,BC 分别相交于点E,F.
求证:OE=OF.
典题精讲
已知 ABCD 的对角线AC 与BD 相交于点O,OA,OB,AB 他的长分别为3,4,5,求其他各边以及两条对角线的长度.
因为平行四边形的对角线互相平分,
所以AC=2OA=6 ,BD=2OB=8 .
又因为OA 2+OB 2=32+42=52=AB 2,所以AC⊥BD.
由勾股定理,可得AD 2=OA 2+OD 2,
而OD=OB,所以AD 2=32+42.
所以AD=5. 同理,可得DC=5,BC=5.
解:
1
典题精讲
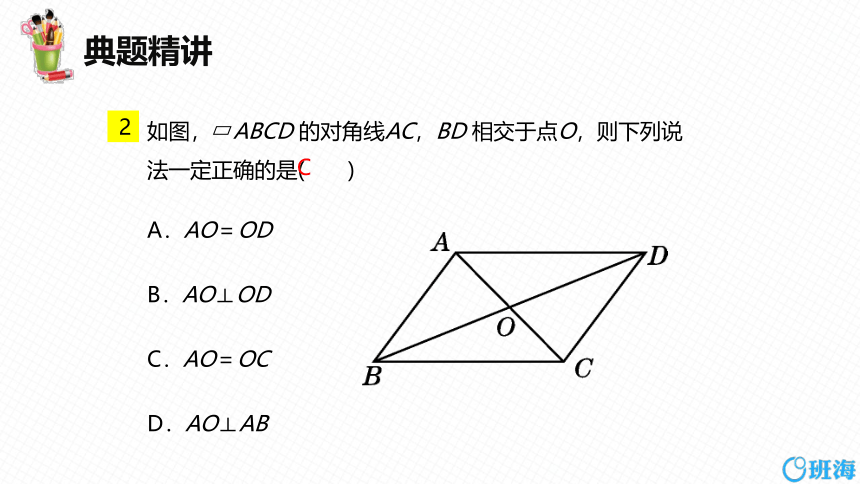
如图, ABCD 的对角线AC,BD 相交于点O,则下列说法一定正确的是( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB
2
C
典题精讲
如图, ABCD 的对角线AC,BD 相交于点O,且AC+BD=16,CD=6,则△ABO 的周长是( )
A.10
B.14
C.20
D.22
3
B
典题精讲
如图, ABCD 的对角线AC 与BD 相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE 的长为( )
A.
B.
C.
D.
4
D
探索新知
2
知识点
平行四边形的面积
1.面积公式:
平行四边形的面积=底×高(底为平行四边形的任意一条边,高为这条边与其对边间的距离);
2.等底等高的平行四边形的面积相等.
探索新知
如图,在 ABCD 中,DE 平分∠ADC,AD=6,BE=2,
则 ABCD 的周长是________.
例3
20
探索新知
求 ABCD 的周长,已知一条边AD=6,只需求出AD 的邻边AB 或CD 的长即可.
∵四边形ABCD 是平行四边形,AD=6,BE=2,
∴AD=BC=6,AD∥BC.
∴EC=BC-BE=6-2=4,∠ADE=∠DEC.
∵DE 平分∠ADC,∴∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD 的周长是2×(4+6)=20.
导引:
探索新知
如图,在 ABCD 中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
例4
B
探索新知
过点A 作AE⊥BC 于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE 的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A 作AE⊥BC 于E,
∵在直角三角形ABE 中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD 的面积=BC · AE=6×2=12.
导引:
探索新知
求平行四边形的面积时,根据平行四边形的面积公式,要知道平行四边形的一边长及这边上的高.平行四边形的高不一定是过顶点的垂线段,因为平行线间的距离处处相等.
总 结
典题精讲
如图,若 ABCD 的周长为36 cm,过点D 分别作AB,BC 边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD 的面积为( )cm2.
A.40
B.32
C.36
D.50
1
A
典题精讲
如图,过 ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH,那么图中的 AEMG 的面积S1与 HCFM 的面积S2 的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.2S1=S2
2
C
典题精讲
如图,在平行四边形ABCD 中,AC,BD 为对角线,BC=6,BC 边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
3
C
易错提醒
如图,在平行四边形ABCD 中,AC 和BD 相交于点O,OE⊥AD 于点E,OF⊥BC 于点F.
试说明:OE=OF.
易错点:容易把未知条件当作已知条件使用
易错提醒
∵四边形ABCD 为平行四边形,
∴OA=OC,∵OE⊥AD 于点E,OF⊥BC 于点F,∴∠AEO=∠CFO=90°,又∠AOE=∠COF,
∴△AOE ≌ △COF,∴OE=OF.
错解误认为已知E,O,F 三点共线,从而得到∠AOE=∠COF,而已知条件中并没有这个.
E,O,F 三点共线需要在解题过程中加以推理,
否则就犯了逻辑错误.
错解:
诊断:
易错提醒
∵四边形ABCD 为平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
∴△AOE ≌ △COF,
∴OE=OF.
正解:
学以致用
小试牛刀
如图,EF 过 ABCD 对角线的交点O,交AD 于E,交BC 于F,若 ABCD 的周长为18,OE=1.5,则四边形EFCD 的周长为( )
A.14
B.13
C.12
D.10
1
C
小试牛刀
如图,在 ABCD 中,对角线AC,BD 相交于点O,AE⊥BD 于点E,CF⊥BD 于点F,连接AF,CE,则下列结论:
①CF=AE;
②OE=OF;
③DE=BF;
④图中共有四对全等三角形.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
2
B
小试牛刀
3 如图,在 ABCD 中,BE⊥AC,垂足E 在CA 的延长线上,DF⊥AC,垂足F 在AC 的延长线上,求证:AE=CF.
小试牛刀
连接BD,交EF 于点O,如图.
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵BE⊥AC,DF⊥AC,
∴∠E=∠F=90°.
又∵∠BOE=∠DOF,
∴△BOE ≌ △DOF (AAS).
∴OE=OF.
∴OE-OA=OF-OC,即AE=CF.
证明:
小试牛刀
4 如图, ABCD 的对角线AC,BD 相交于点O,EF 过点O且与AB,CD 分别相交于点E,F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC 的周长是10,求 ABCD 的周长.
小试牛刀
∵四边形ABCD 是平行四边形,
∴OD=OB,DC∥AB.
∴∠FDO=∠EBO.
在△DFO 和△BEO 中,
∠FDO=∠EBO,
OD=OB,
∠FOD=∠EOB,
∴△DFO ≌ △BEO (ASA).
∴OE=OF.
(1)证明:
小试牛刀
∵四边形ABCD 是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,∴AE=CE.
∵△BEC 的周长是10,
∴BC+BE+CE=BC+BE+AE=BC+AB=10.
∴ ABCD 的周长=2(BC+AB )=20.
(2)解:
小试牛刀
5 如图,四边形ABCD 为平行四边形,∠BAD 的平分线AE 交CD 于点F,交BC 的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求 ABCD 的面积.
小试牛刀
∵四边形ABCD 是平行四边形,
∴AD∥BC,BA=CD.
∴∠DAE=∠E.
又∵AE 平分∠BAD,
∴∠BAE=∠DAE. ∴∠BAE=∠E.
∴BA=BE,∴BE=CD.
(1)证明:
小试牛刀
∵∠BEA=60°,BA=BE,
∴△ABE 为等边三角形.
∵BF⊥AE,∴F 为AE 的中点,
∴AF=EF.
在△AFD 和△EFC 中,
∠DAF=∠E,
AF=EF,
∠AFD=∠EFC,
(2)解:
小试牛刀
∴△AFD ≌ △EFC (ASA).
∴△AFD 的面积等于△EFC 的面积.
∴ ABCD 的面积等于△ABE 的面积.
在Rt△ABF 中,AB=4,AF=EF=2,∴BF=2
∴△ABE 的面积为 ×4×2 =4
∴ ABCD 的面积为4
小试牛刀
6 如图①,四边形ABCD 是平行四边形,对角线AC,BD 相交于点O,过点O 作直线EF 分别交AD,BC 于点E,F.
(1)求证:OE=OF.
(2)如图②,若过O 点的直线EF 与BA,DC 的延长线分别交于点E,F,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?
小试牛刀
∵四边形ABCD 是平行四边形,
∴AD∥BC,AO=CO.
∴∠EAO=∠FCO.
∵∠AOE=∠COF,
∴△AOE ≌ △COF.
∴OE=OF.
(1)证明:
小试牛刀
能得到OE=OF,方法同(1).一般性结论:经过平行四边形的对角线的交点的直线被平行四边形的对边或对边的延长线截得的线段被平行四边形的对角线的交点平分.
(2)解:
课堂小结
课堂小结
1. 平行四边形的对角线互相平分.
2. 平行四边形的面积=底×高(底为平行四边形的
任意一条边,高为这条边与其对边间的距离).
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
1.平行四边形的性质
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平行四边形的性质:
对边相等;
对角相等
回顾旧知
新课精讲
探索新知
1
知识点
平行四边形的性质——对角线互相平分
在上一课的“做一做”中,我们还发现:平行四边形的对角线互相平分. 请你尝试证明这一结论.
探索新知
已知:如图, ABCD 的两条对角线AC 与BD 相交于点O.求证:OA=OC,OB=OD.
∵四边形ABCD 是平行四边形,
∴AB=CD (平行四边形的对边相等),
AB∥CD (平行四边形的定义).
∴∠BAO=∠DCO,∠ABO=∠CDO.
∴△ABO ≌ △CDO.
∴OA=OC,OB=OD.
你还有其他证明方法吗?与同伴交流.
证明:
例1
探索新知
定理 平行四边形的对角线互相平分.
总 结
探索新知
对角线的性质:平行四边形的对角线互相平分.
数学表达式:
如图,∵四边形ABCD 是平行四边形,
对角线AC,BD 相交于点O,
∴OA=OC,OB=OD.
探索新知
例2
证明:
∵四边形ABCD 是平行四边形,
∴DO=BO (平行四边形的对角线互相平分),
AD∥BC (平行四边形的定义).
∴∠ODE=∠OBF.
∵∠DOE=∠BOF,
∴△DOE ≌ △BOF. ∴OE=OF.
已知:如图, ABCD 的对角线AC 与BD 相交于点O,
过点O 的直线与AD,BC 分别相交于点E,F.
求证:OE=OF.
典题精讲
已知 ABCD 的对角线AC 与BD 相交于点O,OA,OB,AB 他的长分别为3,4,5,求其他各边以及两条对角线的长度.
因为平行四边形的对角线互相平分,
所以AC=2OA=6 ,BD=2OB=8 .
又因为OA 2+OB 2=32+42=52=AB 2,所以AC⊥BD.
由勾股定理,可得AD 2=OA 2+OD 2,
而OD=OB,所以AD 2=32+42.
所以AD=5. 同理,可得DC=5,BC=5.
解:
1
典题精讲
如图, ABCD 的对角线AC,BD 相交于点O,则下列说法一定正确的是( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB
2
C
典题精讲
如图, ABCD 的对角线AC,BD 相交于点O,且AC+BD=16,CD=6,则△ABO 的周长是( )
A.10
B.14
C.20
D.22
3
B
典题精讲
如图, ABCD 的对角线AC 与BD 相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE 的长为( )
A.
B.
C.
D.
4
D
探索新知
2
知识点
平行四边形的面积
1.面积公式:
平行四边形的面积=底×高(底为平行四边形的任意一条边,高为这条边与其对边间的距离);
2.等底等高的平行四边形的面积相等.
探索新知
如图,在 ABCD 中,DE 平分∠ADC,AD=6,BE=2,
则 ABCD 的周长是________.
例3
20
探索新知
求 ABCD 的周长,已知一条边AD=6,只需求出AD 的邻边AB 或CD 的长即可.
∵四边形ABCD 是平行四边形,AD=6,BE=2,
∴AD=BC=6,AD∥BC.
∴EC=BC-BE=6-2=4,∠ADE=∠DEC.
∵DE 平分∠ADC,∴∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD 的周长是2×(4+6)=20.
导引:
探索新知
如图,在 ABCD 中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
例4
B
探索新知
过点A 作AE⊥BC 于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE 的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A 作AE⊥BC 于E,
∵在直角三角形ABE 中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD 的面积=BC · AE=6×2=12.
导引:
探索新知
求平行四边形的面积时,根据平行四边形的面积公式,要知道平行四边形的一边长及这边上的高.平行四边形的高不一定是过顶点的垂线段,因为平行线间的距离处处相等.
总 结
典题精讲
如图,若 ABCD 的周长为36 cm,过点D 分别作AB,BC 边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD 的面积为( )cm2.
A.40
B.32
C.36
D.50
1
A
典题精讲
如图,过 ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH,那么图中的 AEMG 的面积S1与 HCFM 的面积S2 的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.2S1=S2
2
C
典题精讲
如图,在平行四边形ABCD 中,AC,BD 为对角线,BC=6,BC 边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
3
C
易错提醒
如图,在平行四边形ABCD 中,AC 和BD 相交于点O,OE⊥AD 于点E,OF⊥BC 于点F.
试说明:OE=OF.
易错点:容易把未知条件当作已知条件使用
易错提醒
∵四边形ABCD 为平行四边形,
∴OA=OC,∵OE⊥AD 于点E,OF⊥BC 于点F,∴∠AEO=∠CFO=90°,又∠AOE=∠COF,
∴△AOE ≌ △COF,∴OE=OF.
错解误认为已知E,O,F 三点共线,从而得到∠AOE=∠COF,而已知条件中并没有这个.
E,O,F 三点共线需要在解题过程中加以推理,
否则就犯了逻辑错误.
错解:
诊断:
易错提醒
∵四边形ABCD 为平行四边形,
∴AD∥BC,OA=OC,
∴∠EAO=∠FCO,
∵OE⊥AD,OF⊥BC,
∴∠AEO=∠CFO=90°,
∴△AOE ≌ △COF,
∴OE=OF.
正解:
学以致用
小试牛刀
如图,EF 过 ABCD 对角线的交点O,交AD 于E,交BC 于F,若 ABCD 的周长为18,OE=1.5,则四边形EFCD 的周长为( )
A.14
B.13
C.12
D.10
1
C
小试牛刀
如图,在 ABCD 中,对角线AC,BD 相交于点O,AE⊥BD 于点E,CF⊥BD 于点F,连接AF,CE,则下列结论:
①CF=AE;
②OE=OF;
③DE=BF;
④图中共有四对全等三角形.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
2
B
小试牛刀
3 如图,在 ABCD 中,BE⊥AC,垂足E 在CA 的延长线上,DF⊥AC,垂足F 在AC 的延长线上,求证:AE=CF.
小试牛刀
连接BD,交EF 于点O,如图.
∵四边形ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵BE⊥AC,DF⊥AC,
∴∠E=∠F=90°.
又∵∠BOE=∠DOF,
∴△BOE ≌ △DOF (AAS).
∴OE=OF.
∴OE-OA=OF-OC,即AE=CF.
证明:
小试牛刀
4 如图, ABCD 的对角线AC,BD 相交于点O,EF 过点O且与AB,CD 分别相交于点E,F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC 的周长是10,求 ABCD 的周长.
小试牛刀
∵四边形ABCD 是平行四边形,
∴OD=OB,DC∥AB.
∴∠FDO=∠EBO.
在△DFO 和△BEO 中,
∠FDO=∠EBO,
OD=OB,
∠FOD=∠EOB,
∴△DFO ≌ △BEO (ASA).
∴OE=OF.
(1)证明:
小试牛刀
∵四边形ABCD 是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,∴AE=CE.
∵△BEC 的周长是10,
∴BC+BE+CE=BC+BE+AE=BC+AB=10.
∴ ABCD 的周长=2(BC+AB )=20.
(2)解:
小试牛刀
5 如图,四边形ABCD 为平行四边形,∠BAD 的平分线AE 交CD 于点F,交BC 的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求 ABCD 的面积.
小试牛刀
∵四边形ABCD 是平行四边形,
∴AD∥BC,BA=CD.
∴∠DAE=∠E.
又∵AE 平分∠BAD,
∴∠BAE=∠DAE. ∴∠BAE=∠E.
∴BA=BE,∴BE=CD.
(1)证明:
小试牛刀
∵∠BEA=60°,BA=BE,
∴△ABE 为等边三角形.
∵BF⊥AE,∴F 为AE 的中点,
∴AF=EF.
在△AFD 和△EFC 中,
∠DAF=∠E,
AF=EF,
∠AFD=∠EFC,
(2)解:
小试牛刀
∴△AFD ≌ △EFC (ASA).
∴△AFD 的面积等于△EFC 的面积.
∴ ABCD 的面积等于△ABE 的面积.
在Rt△ABF 中,AB=4,AF=EF=2,∴BF=2
∴△ABE 的面积为 ×4×2 =4
∴ ABCD 的面积为4
小试牛刀
6 如图①,四边形ABCD 是平行四边形,对角线AC,BD 相交于点O,过点O 作直线EF 分别交AD,BC 于点E,F.
(1)求证:OE=OF.
(2)如图②,若过O 点的直线EF 与BA,DC 的延长线分别交于点E,F,能得到(1)中的结论吗?由此你能得到什么样的一般性结论?
小试牛刀
∵四边形ABCD 是平行四边形,
∴AD∥BC,AO=CO.
∴∠EAO=∠FCO.
∵∠AOE=∠COF,
∴△AOE ≌ △COF.
∴OE=OF.
(1)证明:
小试牛刀
能得到OE=OF,方法同(1).一般性结论:经过平行四边形的对角线的交点的直线被平行四边形的对边或对边的延长线截得的线段被平行四边形的对角线的交点平分.
(2)解:
课堂小结
课堂小结
1. 平行四边形的对角线互相平分.
2. 平行四边形的面积=底×高(底为平行四边形的
任意一条边,高为这条边与其对边间的距离).
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
