专项训练 勾股定理与方程思想在矩形中的应用(含答案)
文档属性
| 名称 | 专项训练 勾股定理与方程思想在矩形中的应用(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 12:33:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
勾股定理与方程思想在矩形中的应用
应用一:矩形+折叠
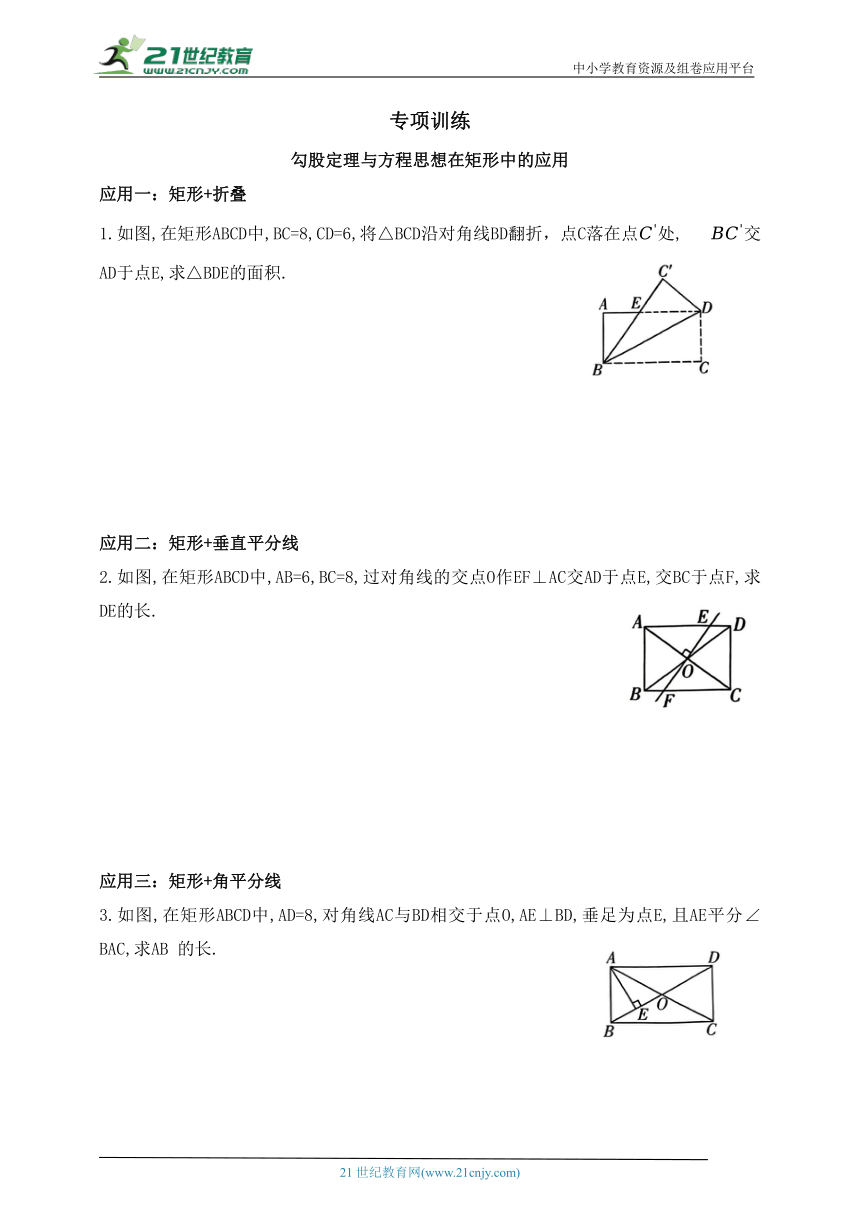
1.如图,在矩形ABCD中,BC=8,CD=6,将△BCD沿对角线BD翻折,点C落在点处, 交AD于点E,求△BDE的面积.
应用二:矩形+垂直平分线
2.如图,在矩形ABCD中,AB=6,BC=8,过对角线的交点O作EF⊥AC交AD于点E,交BC于点F,求DE的长.
应用三:矩形+角平分线
3.如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,且AE平分∠BAC,求AB 的长.
应用四:勾股定理的连续应用
4.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O 的直线分别交AB,CD于点E,F.
(1)求证:四边形BEDF是平行四边形.
(2)当DE=DF时,求EF的长.
参考答案
1.解:∵四边形ABCD为矩形,∴AB=CD=6,AD=BC=8,AD∥BC.
∵矩形纸片ABCD沿对角线BD折叠,∴∠DBC=∠DBE.
∵AD∥BC,∴∠DBC=∠BDE,∴∠BDE=∠EBD,∴EB=ED.设ED=x,则EB=x,AE=8-x.
在Rt△ABE中,∵AB +AE =BE ,∴6 +(8-x) =x , 解得
的面积
2.解:如图,连接CE.∵四边形ABCD是矩形,∴∠ADC=90°,CD=AB=6,AD=BC=8,OA=OC.
∵EF⊥AC,∴AE=CE.设DE=x,则CE=AE=8-x.
在Rt△CDE 中,由勾股定理得x +6 =(8-x) , 解得即
3.解:∵四边形ABCD是矩形,∴AO=CO=BO=DO.
∵AE平分∠BAO,∴∠BAE=∠EAO.
∵AE⊥BD,∴∠AEB=∠AEO=90°,且AE=AE,
∴△ABE≌△AOE(ASA),∴AO=AB,∴AO=AB=BO=DO,∴BD=2AB.
∵AD +AB =BD ,∴64+AB =4AB ,
4.(1)证明:∵四边形ABCD是矩形,∴AB∥CD,OD=OB,∴∠FDO=∠EBO.
又∵∠DOF=∠BOE,∴△DOF≌△BOE(ASA),∴DF=BE.
又∵DF∥BE,∴四边形BEDF是平行四边形.
(2)解:∵DE=DF,四边形BEDF是平行四边形,∴四边形BEDF是菱形,
∴DE=BE,EF⊥BD,OE=OF.
设AE=x,则DE=BE=8-x.
在Rt△ADE中,AE +AD =DE ,∴x +6 =(8-x) ,解得
在Rt△ABD中, AB +
在Rt△DOE中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
勾股定理与方程思想在矩形中的应用
应用一:矩形+折叠
1.如图,在矩形ABCD中,BC=8,CD=6,将△BCD沿对角线BD翻折,点C落在点处, 交AD于点E,求△BDE的面积.
应用二:矩形+垂直平分线
2.如图,在矩形ABCD中,AB=6,BC=8,过对角线的交点O作EF⊥AC交AD于点E,交BC于点F,求DE的长.
应用三:矩形+角平分线
3.如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,且AE平分∠BAC,求AB 的长.
应用四:勾股定理的连续应用
4.如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O 的直线分别交AB,CD于点E,F.
(1)求证:四边形BEDF是平行四边形.
(2)当DE=DF时,求EF的长.
参考答案
1.解:∵四边形ABCD为矩形,∴AB=CD=6,AD=BC=8,AD∥BC.
∵矩形纸片ABCD沿对角线BD折叠,∴∠DBC=∠DBE.
∵AD∥BC,∴∠DBC=∠BDE,∴∠BDE=∠EBD,∴EB=ED.设ED=x,则EB=x,AE=8-x.
在Rt△ABE中,∵AB +AE =BE ,∴6 +(8-x) =x , 解得
的面积
2.解:如图,连接CE.∵四边形ABCD是矩形,∴∠ADC=90°,CD=AB=6,AD=BC=8,OA=OC.
∵EF⊥AC,∴AE=CE.设DE=x,则CE=AE=8-x.
在Rt△CDE 中,由勾股定理得x +6 =(8-x) , 解得即
3.解:∵四边形ABCD是矩形,∴AO=CO=BO=DO.
∵AE平分∠BAO,∴∠BAE=∠EAO.
∵AE⊥BD,∴∠AEB=∠AEO=90°,且AE=AE,
∴△ABE≌△AOE(ASA),∴AO=AB,∴AO=AB=BO=DO,∴BD=2AB.
∵AD +AB =BD ,∴64+AB =4AB ,
4.(1)证明:∵四边形ABCD是矩形,∴AB∥CD,OD=OB,∴∠FDO=∠EBO.
又∵∠DOF=∠BOE,∴△DOF≌△BOE(ASA),∴DF=BE.
又∵DF∥BE,∴四边形BEDF是平行四边形.
(2)解:∵DE=DF,四边形BEDF是平行四边形,∴四边形BEDF是菱形,
∴DE=BE,EF⊥BD,OE=OF.
设AE=x,则DE=BE=8-x.
在Rt△ADE中,AE +AD =DE ,∴x +6 =(8-x) ,解得
在Rt△ABD中, AB +
在Rt△DOE中,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
