1.1圆柱和圆锥的认识课时训练-小学数学六年级下册北师大版(含解析)
文档属性
| 名称 | 1.1圆柱和圆锥的认识课时训练-小学数学六年级下册北师大版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
1.1圆柱和圆锥的认识课时训练-小学数学六年级下册北师大版
一、选择题
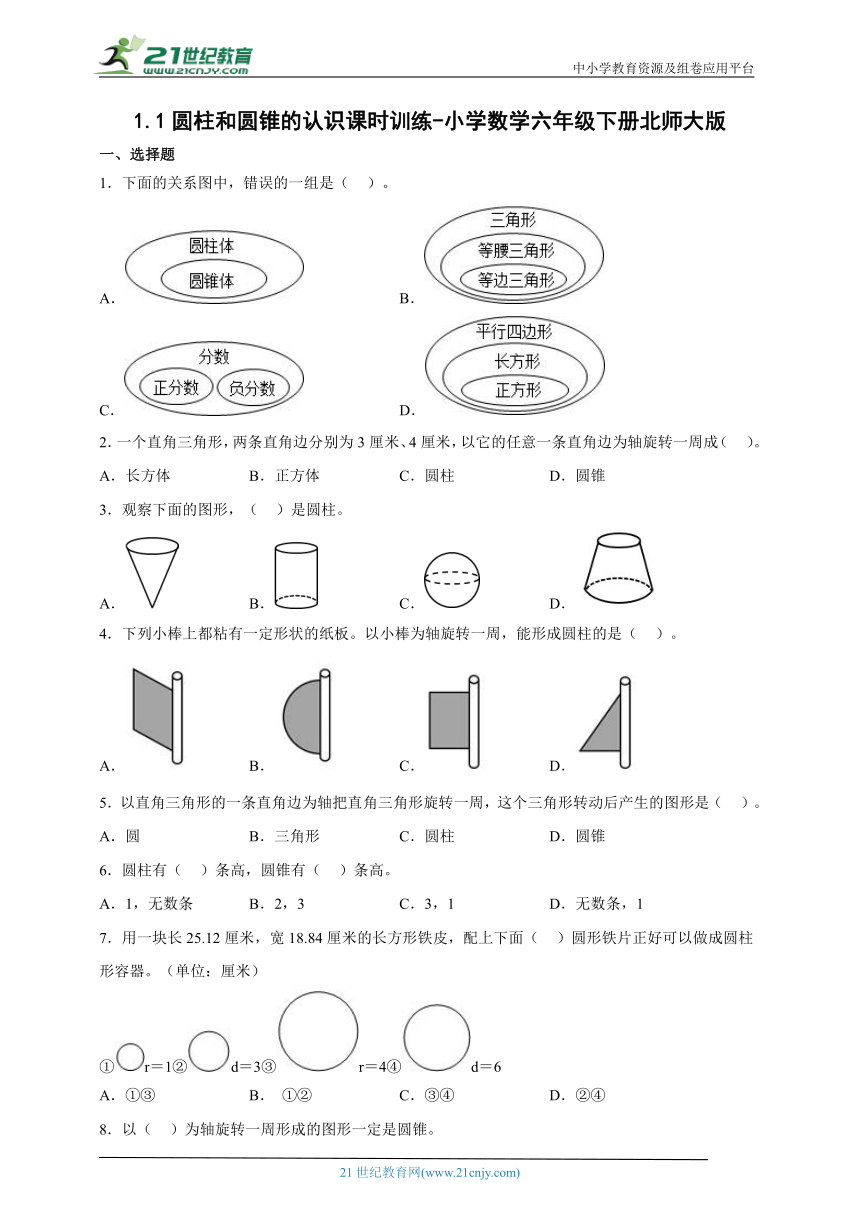
1.下面的关系图中,错误的一组是( )。
A. B.
C. D.
2.一个直角三角形,两条直角边分别为3厘米、4厘米,以它的任意一条直角边为轴旋转一周成( )。
A.长方体 B.正方体 C.圆柱 D.圆锥
3.观察下面的图形,( )是圆柱。
A. B. C. D.
4.下列小棒上都粘有一定形状的纸板。以小棒为轴旋转一周,能形成圆柱的是( )。
A. B. C. D.
5.以直角三角形的一条直角边为轴把直角三角形旋转一周,这个三角形转动后产生的图形是( )。
A.圆 B.三角形 C.圆柱 D.圆锥
6.圆柱有( )条高,圆锥有( )条高。
A.1,无数条 B.2,3 C.3,1 D.无数条,1
7.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面( )圆形铁片正好可以做成圆柱形容器。(单位:厘米)
①r=1②d=3③r=4④d=6
A.①③ B. ①② C.③④ D.②④
8.以( )为轴旋转一周形成的图形一定是圆锥。
A.三角形中任意的一条边 B.直角三角形中任意的一条边
C.直角三角形中的直角边 D.直角三角形中的斜边
二、填空题
9.把一个直角三角形绕着它的一条直角边旋转一周,所得到的图形是一个( )。
10.下图中每个小方格的边长是1分米,当( )分米时。剪下图中的阴影部分恰好可以围成一个圆柱(接头处忽略不计)。
11.从圆锥体的顶点到( )的连线叫做它的高,它有( )条。
12.如图,以三角形4cm的直角边所在的直线为轴旋转一周,可以得到一个( ),它的底面直径是( )cm,高是( )cm。
13.将一个长是5cm,宽是4cm的长方形绕它的一条边所在的直线为轴旋转成一个圆柱,这个圆柱的底面周长可能是( )cm,也可能是( )cm。
14.笑笑到自己家开的小超市帮忙。他把8个同样的圆柱形玻璃杯,按照如图所示的方式紧密地放入纸盒中。这个纸盒的长是( )cm,宽是( )cm,高是( )cm。
三、判断题
15.圆柱的高有无数条,圆锥的高也有无数条。( )
16.一个长方形绕一条长边旋转一周所形成的图形是圆柱。( )
17.一个物体上、下两个面是圆形,那么它一定是圆柱形物体。( )
18.铁丝是圆柱体。( )
19.圆柱有两个面是大小相同的圆,有一个面是曲面.( )
四、解答题
20.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
21.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周。
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
22.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
23.妈妈的茶杯是圆柱形状的,底面直径8厘米,高15厘米,这只茶杯直立放在桌上占据桌面的面积是多少平方厘米?
24.长方体纸盒中装了4筒羽毛球(如图),已知每筒羽毛球的形状为圆柱形,底面半径为4.5cm,高为45cm,这个纸盒的长、宽、高至少是多少厘米?
参考答案:
1.A
【分析】根据三角形、等腰三角形、等边三角形的特征关系,平行四边形、长方形、正方形的特殊关系,分数的组成,圆柱和圆锥的关系来进行选择即可。
【详解】A.圆锥体不是特殊的圆柱体,所以是错误的。
B.等边三角形是特殊的等腰三角形,等边三角形和等腰三角形都是特殊的三角形;
C.分数分为正分数、负分数;
D.正方形是特殊的长方形,长方形和正方形又是特殊的平行四边形。
故答案为:A
【点睛】此题考查的是学生的分析能力和对四边形、正方形、长方形、圆柱、圆锥、三角形、分数特征的掌握熟练程度。
2.D
【分析】根据圆锥的特征:以直角三角形的一条直角边为轴旋转一周,得到的几何体是圆锥体;据此解答。
【详解】根据分析可知,一个直角三角形,两条直角边分别为3厘米、4厘米,以它的任意一条直角边为轴旋转一周成圆锥。
故答案为:D
【点睛】利用圆锥的特征进行解答。
3.B
【分析】根据圆柱的特征,圆柱的上、下面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的对面周长,长方形的宽等于圆柱的高;据此判断即可。
【详解】根据分析可知:
A.是圆锥;
B.是圆柱;
C.是一球体;
D.是圆台。
故答案为:B
【点睛】利用圆柱特征进行解答。
4.C
【分析】根据各平面图形的特征,长方形或正方形绕一边旋转一周得到一个圆柱,由此解答即可。
【详解】长方形或正方形绕一边旋转一周得到一个圆柱。
故答案为:C
【点睛】根据各平面图形的特征及圆柱的特征即可判定。
5.D
【分析】根据点动成线,线动成面,面动成体及直角三角形、圆锥的特征,直角三角形绕一直角边旋转一周产生的图形是以旋转直角边为高,另一直角边为底面半径的圆锥。据此解答即可。
【详解】以直角三角形的一条直角边为轴把直角三角形旋转一周,这个三角形转动后产生的图形是圆锥。
故答案为:D。
【点睛】此题考查的目的是理解圆锥的特征,圆锥的底面是圆,圆锥的顶点到底面圆心的距离是圆锥的高,圆锥的侧面是一个曲面,侧面展开是一个扇形。
6.D
【分析】根据圆柱和圆锥的特征,圆柱有无数条高,圆锥有1条高。
【详解】圆柱有无数条高,圆锥有1条高;
故答案为:D。
【点睛】本题主要考查的是圆柱和圆锥的特征。
7.C
【分析】根据圆柱的特征,利用圆的周长公式:周长=π×直径;直径=周长÷π;用长方形的铁皮的长和宽,分别除以π,求出长围成圆,圆的直径;宽围成圆,圆的直径;再和圆形铁片的直径比较,相等可以做成圆柱形容器,据此解答。
【详解】长围成圆时直径:
25.12÷3.14=8(厘米)
宽围成圆时直径
18.84÷3.14=6(厘米)
①r=1,直径是:1×2=2(厘米),不能和铁片做成圆柱形容器;
②d=3,直径是3厘米,不能和铁片做成圆柱形容器;
③r=4,直径是:4×2=8(厘米),能和铁片做成圆柱形容器;
④d=6,直径是6厘米,能和铁片做成圆柱形容器。
只有③④可以和长方形铁皮做成圆柱形容器。
故答案应选:C。
【点睛】本题考查圆柱的特征,圆的周长公式的应用,关键求出长方形的铁皮的长和宽能围成的圆的直径。
8.C
【分析】以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥,据此解答。
【详解】根据分析可知,直角三角形中的直角边轴,旋转一周形成的圆形一定是圆锥。
故答案为:C
【点睛】本题考查圆锥的特点,根据圆锥的特点进行解答。
9.圆锥
【详解】根据圆锥的定义,直角三角形绕着一条直角边旋转一周,得到的图形是圆锥。
如图:
10.6.28
【分析】由图可知,圆的半径是1分米,要使阴影部分恰好可以围成一个圆柱,则长方形的底边长等于圆的周长,根据圆的周长公式:周长=2×π×半径,代入数据,即可解答。
【详解】x=2×3.14×1
=6.28×1
=6.28(分米)
【点睛】根据圆柱的特征,利用圆的周长公式进行解答。
11. 底面圆心 1
【详解】根据圆锥高的意义:从圆锥的顶点到底面圆心的连线叫做圆锥高;所以从圆锥体的顶点到底面圆心的连线叫做它的高,它有1条。
12. 圆锥体 6 4
【分析】以三角形4cm的直角边所在的直线为轴旋转一周,可以得到一个圆锥体,圆锥的底面半径是3厘米,则它的底面直径是3×2=6(厘米),高是4厘米。
【详解】根据圆锥的定义,以三角形4cm的直角边所在的直线为轴旋转一周,可以得到一个圆锥体,它的底面直径是6cm,高是4cm。
【点睛】本题考查圆锥的认识。掌握圆锥的定义是解题的关键。
13. 25.12 31.4
【分析】绕长边所在的直线为轴旋转成一个底面半径为4厘米的圆柱;绕宽边所在的直线为轴旋转成一个底面半径为5厘米的圆柱;将数据分别代入圆的周长公式计算即可。
【详解】3.14×4×2
=3.14×8
=25.12(cm)
3.14×5×2
=3.14×10
=31.4(cm)
【点睛】明确圆柱的底面半径的值是解答本题的关键。
14. 24 12 10
【分析】从图中可知:长方形纸盒中紧密放入8个同样的圆柱形玻璃杯,长方形纸盒的长为4个圆柱形玻璃杯的直径的和,长方形纸盒的宽为2个圆柱形玻璃杯的直径的和,长方形纸盒的高为圆柱形玻璃杯的高,据此可算出长方形纸盒的长、宽、高。
【详解】长方形纸盒的长:4×6=24cm
长方形纸盒的宽:2×6=12cm
长方形纸盒的高=圆柱形玻璃杯的高=10cm
【点睛】此题主要考查长方体和圆柱的体积关系,若干个圆柱体的体积的和通过等积变形可得到长方体的体积。
15.×
【详解】根据圆柱和圆锥的特征和高的意义,圆柱的两个底面之间的距离叫做圆柱的高;圆柱的高有无数条;圆锥的顶点到底面圆心的距离叫做圆锥的高;圆锥的高只有一条。
原题干说法错误。
故答案为:×
16.√
【分析】根据圆柱的意义,以长方形的一边为旋转轴,其余三边旋转形成的面围成的旋转体叫做圆柱,所以一个长方形绕着长为轴旋转一周,可以得到一个圆柱体,据此解答即可。
【详解】圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。由此可知:一个长方形绕它的一条长旋转一周后得到的图形是圆柱。
故判断正确。
【点睛】一个长方形绕着其中一边旋转一周,可以得到一个圆柱体。
17.×
【分析】根据圆柱的特征进行判断即可。
【详解】圆柱的每一个横截面都是相等的,且圆柱的侧面展开是一个长方形,一个物体上、下两个面是圆形,它不一定是圆柱体,如我们生活中认识的腰鼓,上下的是圆形,但它不是圆柱体,所以,一个物体上、下两个面是圆形,那么它一定是圆柱体说法数错误的。
故答案为:×
【点睛】本题考查圆柱的特征,熟知圆柱的特征解答问题。
18.√
【分析】根据圆柱体的特征,圆柱体的上下面是两个完全相同的圆,侧面是曲面,两个底面之间的距离是圆柱体的高,一个圆柱体有无数条高,这些特征铁丝都满足,所以铁丝是圆柱体。
【详解】根据圆柱体的特征,铁丝(是直的不弯曲)是圆柱体。
所以原题说法正确。
【点睛】此题主要考查学生对圆柱体的特征的理解与实际应用解题能力。
19.√
【详解】根据圆柱的特征:圆柱的上下两个面叫做底面,它们是完全相同的两个圆,圆柱有一个曲面,叫做侧面.可知原题说法正确;
故答案为:√.
【点评】此题考查了圆柱的特征,应理解并灵活运用.
20.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
【点睛】本题考查学生的空间想象能力,分析底面和背面也需要和正面看到一样多的丝带。
21.(1)可以得到一个圆锥,这个图形的高是3cm。
(2)12.56厘米
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm。
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,根据圆的周长公式:周长=2×半径×π,所以底面周长是2×2×3.14=12.56cm,即可解答。
【详解】(1)可以得到一个圆锥,这个图形的高是3cm。
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米。
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律。
22.见详解
【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5cm,底面半径为1cm,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1cm,底面半径为0.5cm,生成圆柱②。
【详解】答:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1cm,圆柱高为0.5cm;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5cm,圆柱高为1cm。
【点睛】一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱。
23.50.24平方厘米
【分析】根据题目可知,这个茶杯是圆柱形,茶杯直立放在桌面上占据桌面的面积就是圆柱的底面圆的面积,根据圆的面积公式:S=πr2,把数代入即可。
【详解】3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这只茶杯直立放在桌面上占据桌面的面积是50.24平方厘米。
【点睛】本题主要考查圆柱的特征,圆柱是由两个底面和一个侧面构成,两个底面是大小相等的圆。
24.45cm,18cm,18cm
【详解】4.5×2×2=18(cm)
答:这个纸盒的长至少是45 cm,宽至少是18 cm,高至少是18 cm。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.1圆柱和圆锥的认识课时训练-小学数学六年级下册北师大版
一、选择题
1.下面的关系图中,错误的一组是( )。
A. B.
C. D.
2.一个直角三角形,两条直角边分别为3厘米、4厘米,以它的任意一条直角边为轴旋转一周成( )。
A.长方体 B.正方体 C.圆柱 D.圆锥
3.观察下面的图形,( )是圆柱。
A. B. C. D.
4.下列小棒上都粘有一定形状的纸板。以小棒为轴旋转一周,能形成圆柱的是( )。
A. B. C. D.
5.以直角三角形的一条直角边为轴把直角三角形旋转一周,这个三角形转动后产生的图形是( )。
A.圆 B.三角形 C.圆柱 D.圆锥
6.圆柱有( )条高,圆锥有( )条高。
A.1,无数条 B.2,3 C.3,1 D.无数条,1
7.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上下面( )圆形铁片正好可以做成圆柱形容器。(单位:厘米)
①r=1②d=3③r=4④d=6
A.①③ B. ①② C.③④ D.②④
8.以( )为轴旋转一周形成的图形一定是圆锥。
A.三角形中任意的一条边 B.直角三角形中任意的一条边
C.直角三角形中的直角边 D.直角三角形中的斜边
二、填空题
9.把一个直角三角形绕着它的一条直角边旋转一周,所得到的图形是一个( )。
10.下图中每个小方格的边长是1分米,当( )分米时。剪下图中的阴影部分恰好可以围成一个圆柱(接头处忽略不计)。
11.从圆锥体的顶点到( )的连线叫做它的高,它有( )条。
12.如图,以三角形4cm的直角边所在的直线为轴旋转一周,可以得到一个( ),它的底面直径是( )cm,高是( )cm。
13.将一个长是5cm,宽是4cm的长方形绕它的一条边所在的直线为轴旋转成一个圆柱,这个圆柱的底面周长可能是( )cm,也可能是( )cm。
14.笑笑到自己家开的小超市帮忙。他把8个同样的圆柱形玻璃杯,按照如图所示的方式紧密地放入纸盒中。这个纸盒的长是( )cm,宽是( )cm,高是( )cm。
三、判断题
15.圆柱的高有无数条,圆锥的高也有无数条。( )
16.一个长方形绕一条长边旋转一周所形成的图形是圆柱。( )
17.一个物体上、下两个面是圆形,那么它一定是圆柱形物体。( )
18.铁丝是圆柱体。( )
19.圆柱有两个面是大小相同的圆,有一个面是曲面.( )
四、解答题
20.今天是红红的生日,同学们送给她一个大蛋糕,蛋糕是圆柱形的。服务员阿姨说要配上十字形的丝带才漂亮。你知道至少要多长的丝带才合适吗?(打结处要10dm)
21.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周。
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
22.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
23.妈妈的茶杯是圆柱形状的,底面直径8厘米,高15厘米,这只茶杯直立放在桌上占据桌面的面积是多少平方厘米?
24.长方体纸盒中装了4筒羽毛球(如图),已知每筒羽毛球的形状为圆柱形,底面半径为4.5cm,高为45cm,这个纸盒的长、宽、高至少是多少厘米?
参考答案:
1.A
【分析】根据三角形、等腰三角形、等边三角形的特征关系,平行四边形、长方形、正方形的特殊关系,分数的组成,圆柱和圆锥的关系来进行选择即可。
【详解】A.圆锥体不是特殊的圆柱体,所以是错误的。
B.等边三角形是特殊的等腰三角形,等边三角形和等腰三角形都是特殊的三角形;
C.分数分为正分数、负分数;
D.正方形是特殊的长方形,长方形和正方形又是特殊的平行四边形。
故答案为:A
【点睛】此题考查的是学生的分析能力和对四边形、正方形、长方形、圆柱、圆锥、三角形、分数特征的掌握熟练程度。
2.D
【分析】根据圆锥的特征:以直角三角形的一条直角边为轴旋转一周,得到的几何体是圆锥体;据此解答。
【详解】根据分析可知,一个直角三角形,两条直角边分别为3厘米、4厘米,以它的任意一条直角边为轴旋转一周成圆锥。
故答案为:D
【点睛】利用圆锥的特征进行解答。
3.B
【分析】根据圆柱的特征,圆柱的上、下面是完全相同的两个圆,侧面是一个曲面,侧面沿高展开是一个长方形,这个长方形的长等于圆柱的对面周长,长方形的宽等于圆柱的高;据此判断即可。
【详解】根据分析可知:
A.是圆锥;
B.是圆柱;
C.是一球体;
D.是圆台。
故答案为:B
【点睛】利用圆柱特征进行解答。
4.C
【分析】根据各平面图形的特征,长方形或正方形绕一边旋转一周得到一个圆柱,由此解答即可。
【详解】长方形或正方形绕一边旋转一周得到一个圆柱。
故答案为:C
【点睛】根据各平面图形的特征及圆柱的特征即可判定。
5.D
【分析】根据点动成线,线动成面,面动成体及直角三角形、圆锥的特征,直角三角形绕一直角边旋转一周产生的图形是以旋转直角边为高,另一直角边为底面半径的圆锥。据此解答即可。
【详解】以直角三角形的一条直角边为轴把直角三角形旋转一周,这个三角形转动后产生的图形是圆锥。
故答案为:D。
【点睛】此题考查的目的是理解圆锥的特征,圆锥的底面是圆,圆锥的顶点到底面圆心的距离是圆锥的高,圆锥的侧面是一个曲面,侧面展开是一个扇形。
6.D
【分析】根据圆柱和圆锥的特征,圆柱有无数条高,圆锥有1条高。
【详解】圆柱有无数条高,圆锥有1条高;
故答案为:D。
【点睛】本题主要考查的是圆柱和圆锥的特征。
7.C
【分析】根据圆柱的特征,利用圆的周长公式:周长=π×直径;直径=周长÷π;用长方形的铁皮的长和宽,分别除以π,求出长围成圆,圆的直径;宽围成圆,圆的直径;再和圆形铁片的直径比较,相等可以做成圆柱形容器,据此解答。
【详解】长围成圆时直径:
25.12÷3.14=8(厘米)
宽围成圆时直径
18.84÷3.14=6(厘米)
①r=1,直径是:1×2=2(厘米),不能和铁片做成圆柱形容器;
②d=3,直径是3厘米,不能和铁片做成圆柱形容器;
③r=4,直径是:4×2=8(厘米),能和铁片做成圆柱形容器;
④d=6,直径是6厘米,能和铁片做成圆柱形容器。
只有③④可以和长方形铁皮做成圆柱形容器。
故答案应选:C。
【点睛】本题考查圆柱的特征,圆的周长公式的应用,关键求出长方形的铁皮的长和宽能围成的圆的直径。
8.C
【分析】以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥,据此解答。
【详解】根据分析可知,直角三角形中的直角边轴,旋转一周形成的圆形一定是圆锥。
故答案为:C
【点睛】本题考查圆锥的特点,根据圆锥的特点进行解答。
9.圆锥
【详解】根据圆锥的定义,直角三角形绕着一条直角边旋转一周,得到的图形是圆锥。
如图:
10.6.28
【分析】由图可知,圆的半径是1分米,要使阴影部分恰好可以围成一个圆柱,则长方形的底边长等于圆的周长,根据圆的周长公式:周长=2×π×半径,代入数据,即可解答。
【详解】x=2×3.14×1
=6.28×1
=6.28(分米)
【点睛】根据圆柱的特征,利用圆的周长公式进行解答。
11. 底面圆心 1
【详解】根据圆锥高的意义:从圆锥的顶点到底面圆心的连线叫做圆锥高;所以从圆锥体的顶点到底面圆心的连线叫做它的高,它有1条。
12. 圆锥体 6 4
【分析】以三角形4cm的直角边所在的直线为轴旋转一周,可以得到一个圆锥体,圆锥的底面半径是3厘米,则它的底面直径是3×2=6(厘米),高是4厘米。
【详解】根据圆锥的定义,以三角形4cm的直角边所在的直线为轴旋转一周,可以得到一个圆锥体,它的底面直径是6cm,高是4cm。
【点睛】本题考查圆锥的认识。掌握圆锥的定义是解题的关键。
13. 25.12 31.4
【分析】绕长边所在的直线为轴旋转成一个底面半径为4厘米的圆柱;绕宽边所在的直线为轴旋转成一个底面半径为5厘米的圆柱;将数据分别代入圆的周长公式计算即可。
【详解】3.14×4×2
=3.14×8
=25.12(cm)
3.14×5×2
=3.14×10
=31.4(cm)
【点睛】明确圆柱的底面半径的值是解答本题的关键。
14. 24 12 10
【分析】从图中可知:长方形纸盒中紧密放入8个同样的圆柱形玻璃杯,长方形纸盒的长为4个圆柱形玻璃杯的直径的和,长方形纸盒的宽为2个圆柱形玻璃杯的直径的和,长方形纸盒的高为圆柱形玻璃杯的高,据此可算出长方形纸盒的长、宽、高。
【详解】长方形纸盒的长:4×6=24cm
长方形纸盒的宽:2×6=12cm
长方形纸盒的高=圆柱形玻璃杯的高=10cm
【点睛】此题主要考查长方体和圆柱的体积关系,若干个圆柱体的体积的和通过等积变形可得到长方体的体积。
15.×
【详解】根据圆柱和圆锥的特征和高的意义,圆柱的两个底面之间的距离叫做圆柱的高;圆柱的高有无数条;圆锥的顶点到底面圆心的距离叫做圆锥的高;圆锥的高只有一条。
原题干说法错误。
故答案为:×
16.√
【分析】根据圆柱的意义,以长方形的一边为旋转轴,其余三边旋转形成的面围成的旋转体叫做圆柱,所以一个长方形绕着长为轴旋转一周,可以得到一个圆柱体,据此解答即可。
【详解】圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。由此可知:一个长方形绕它的一条长旋转一周后得到的图形是圆柱。
故判断正确。
【点睛】一个长方形绕着其中一边旋转一周,可以得到一个圆柱体。
17.×
【分析】根据圆柱的特征进行判断即可。
【详解】圆柱的每一个横截面都是相等的,且圆柱的侧面展开是一个长方形,一个物体上、下两个面是圆形,它不一定是圆柱体,如我们生活中认识的腰鼓,上下的是圆形,但它不是圆柱体,所以,一个物体上、下两个面是圆形,那么它一定是圆柱体说法数错误的。
故答案为:×
【点睛】本题考查圆柱的特征,熟知圆柱的特征解答问题。
18.√
【分析】根据圆柱体的特征,圆柱体的上下面是两个完全相同的圆,侧面是曲面,两个底面之间的距离是圆柱体的高,一个圆柱体有无数条高,这些特征铁丝都满足,所以铁丝是圆柱体。
【详解】根据圆柱体的特征,铁丝(是直的不弯曲)是圆柱体。
所以原题说法正确。
【点睛】此题主要考查学生对圆柱体的特征的理解与实际应用解题能力。
19.√
【详解】根据圆柱的特征:圆柱的上下两个面叫做底面,它们是完全相同的两个圆,圆柱有一个曲面,叫做侧面.可知原题说法正确;
故答案为:√.
【点评】此题考查了圆柱的特征,应理解并灵活运用.
20.50分米
【分析】由图可知,捆扎这个盒子至少用去4个底面直径和4个高长度的和,再加上打结用去丝带的长度10分米,据此解答。
【详解】6×4+4×4+10
=24+16+10
=40+10
=50(分米)
答:至少要50分米的丝带才合适。
【点睛】本题考查学生的空间想象能力,分析底面和背面也需要和正面看到一样多的丝带。
21.(1)可以得到一个圆锥,这个图形的高是3cm。
(2)12.56厘米
【分析】(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm。
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,根据圆的周长公式:周长=2×半径×π,所以底面周长是2×2×3.14=12.56cm,即可解答。
【详解】(1)可以得到一个圆锥,这个图形的高是3cm。
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米。
【点评】解答此题的关键是掌握圆锥的特征和面动成体的规律。
22.见详解
【分析】根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5cm,底面半径为1cm,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1cm,底面半径为0.5cm,生成圆柱②。
【详解】答:圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1cm,圆柱高为0.5cm;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5cm,圆柱高为1cm。
【点睛】一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱。
23.50.24平方厘米
【分析】根据题目可知,这个茶杯是圆柱形,茶杯直立放在桌面上占据桌面的面积就是圆柱的底面圆的面积,根据圆的面积公式:S=πr2,把数代入即可。
【详解】3.14×(8÷2)2
=3.14×16
=50.24(平方厘米)
答:这只茶杯直立放在桌面上占据桌面的面积是50.24平方厘米。
【点睛】本题主要考查圆柱的特征,圆柱是由两个底面和一个侧面构成,两个底面是大小相等的圆。
24.45cm,18cm,18cm
【详解】4.5×2×2=18(cm)
答:这个纸盒的长至少是45 cm,宽至少是18 cm,高至少是18 cm。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
