江西省重点中学协作体2014届高三第一次联考数学(文)试题
文档属性
| 名称 | 江西省重点中学协作体2014届高三第一次联考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 311.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-17 00:00:00 | ||
图片预览




文档简介
江西省重点中学协作体2014届高三第一次联考
数学文试题
考试时间:120分钟 分值:150分
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若复数(为虚数单位),是的模,则的虚部是( )
A. B. C.1 D.
2.若集合A={直线},B={圆},则集合(A∩B)所含元素个数为( )
A.0或1或2 B.0 C.1 D.2
3.已知,则( )
A. B. C. D.
4.已知变量具有线性相关关系,测得的一组数据如下:,其回归方程为,则的值等于( )
A.0.9 B.0.8 C.0.6 D.0.2
5. “”是“”的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
6.若,则的解集为( )
A. B.
C. D.
7.执行如图所示的程序框图,若输入,则输出的
( )
A. B. C. D.
8.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,该四棱锥表面积和体积分别是( )
A. B.
C. D.8,8
9.抛物线绕轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )
A.1 B.2 C.3 D.
10.已知函数(k≠0),定义函数
,给出下列命题:
①函数是奇函数;②;③当k<0,若mn<0,m+n<0,总有成立,其中所有正确命题的个数是( )
A.0 B.1 C.2 D.3
二.填空题:(本大题共5小题,每小题5分,共25分;把答案写在答题卷中对应题号的横线上。)
11.已知向量 ,若∥,则·=_______.
12.设等差数列、等比数列首项都是1,公差与公比都是2,则 .
13.已知函数是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式恒成立,则不等式的解集为 .
14.在平面直角坐标系XOY中,圆C的方程为,若直线上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围是 .
15.已知函数,等于抛掷一颗均匀的正六面体骰子得到的点数,则在上有偶数个零点的概率是 .
三、解答题:(本大题共6小题,共75分;写出必要的文字说明、证明过程或演算步骤)
16.(本小题满分12分)已知数列中,,(为数列的前n项和),数列为等差数列且满足,;
(1)求数列的通项公式;(2)设数列的前n项和为Tn,求Tn.
17.(本小题满分12分)在△中,内角,,的对边边长分别为,,,且.
(1)判断△的形状; (2)若,则△的面积是多少?
18.(本小题满分12分)通过随机调查九校高三100名学生在高二文理分科是否与性别有关,得到如下的列联表:(单位:人)
(1)从这50名女生中按文理采取分层抽样,抽取一个容量为5的样本,问样本中文科生与理科生各多少人?
(2)从(1)中抽到的5名女生中随机选取两名访谈,求选到文科生、理科生各一名的概率;
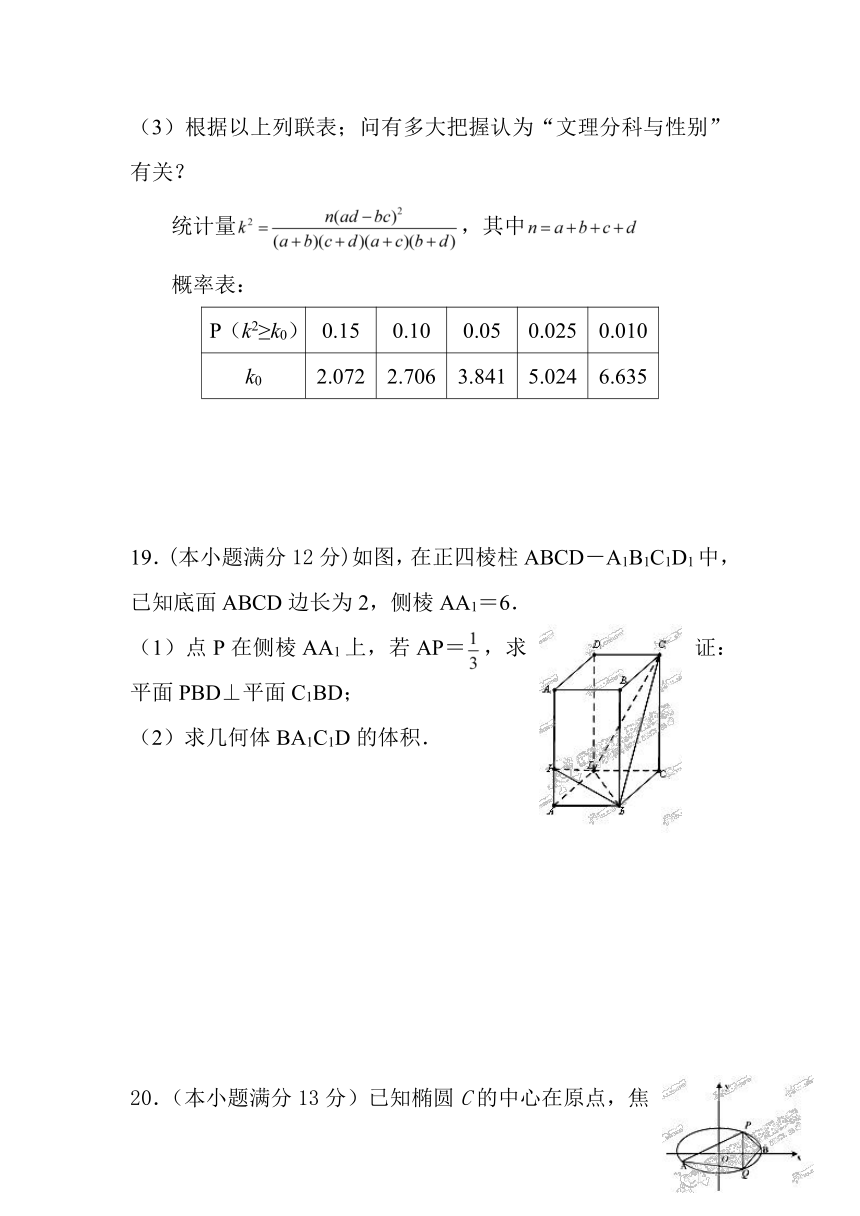
(3)根据以上列联表;问有多大把握认为“文理分科与性别”有关?
统计量,其中
概率表:
P(k2≥k0)
0.15
0.10
0.05
0.025
0.010
k0
2.072
2.706
3.841
5.024
6.635
19.(本小题满分12分)如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
(1)点P在侧棱AA1上,若AP=,求证:平面PBD⊥平面C1BD;
(2)求几何体BA1C1D的体积.
20.(本小题满分13分)已知椭圆C的中心在原点,焦点在轴上,离心率等于,它的一个顶点恰好是抛物线的焦点.
(1)求椭圆C的方程;
(2)、是椭圆上两点,A、B是椭圆位于直线PQ两侧的两动点,当A、B运动时,满足,试问直线AB的斜率是否为定值,请说明理由.
21.(本小题满分14分)已知,设函数 .
(1)求函数的单调区间;
(2)是否存在整数t,对于任意,关于x的方程在区间上有唯一实数解,若存在,求t的值;若不存在,说明理由.
江西省重点中学协作体2014届高三第一次联考数学(文)
参考答案
选择题(本大题共10小题,每小题5分,共50分)
二.填空题(本大题共5小题,每小题5分,共25分)
11. -10 12. 57 13. 14. 15.
三.简答题(共75分)
(2)由(1)知
∵为等差数列
∴其公差
∴
∴…………………………………9分
∴当时,
当时,
综上可知……………………………12分
17. 答案:(1)由得,
即,即,
所以或,
即或. ………………………………………………3分
因为,所以,即,所以不成立,舍去,
所以,即.所以△是直角三角形。……………………………6分
18.(1)文科生3人,理科生2人…………………………………………4分
(2)设三名文科生分别为文1、文2、文3,两名理科生分别为理1、理2、,则从中任选两人的结果为(文1,文2)、(文1,文3)、(文1,理1)、(文1,理2)、(文2,文3)、(文2,理1)、(文2,理2)、(文3,理1)、(文3,理2)、(理1,理2)共10种情况,其中一文一理的共6种。
∴…………………………………………8分
(3)
∴有99%的把握认为 “文理分科与性别”有关。……………………………………12分
19.(1)连结AC交BD于点O,连结C1O,PO
∵正四棱柱ABCD-A1B1C1D1
∴C1C⊥平面ABCD且O为BD、AC中点
∴C1C⊥CD C1C⊥BC
又∵正四棱柱ABCD-A1B1C1D1 ∴CD=CB ∴C1D=C1B ∴C1O⊥BD
又
∴C1O⊥OP ∵OP∩BD=0
又PO 平面PBD BD 平面PBD ∴C1O⊥平面 又∵C1O 平面C1BD
∴平面PBD⊥平面C1BD…………………………………………6分
…………………………………………12分
(2)∵,则PA、PB的斜率之和为0,设直线PA的斜率为,则PB的斜率为,
PA的直线方程为,设A(x1、y1),B(x2、y2)
由.将(1)代入(2)整理得,
有.同理PB的直线方程为,
可得,∴,.
从而====,
所以的斜率为定值.………………………………………………13分
故函数在R上单调递减
当时,方程的两个实根为
则时,;时,,时,
故函数的单调递减区间为、
单调递增区间为…………………………………6分
1)当时,,解得
∴关于x的方程有唯一实数解
∴,故在上单调递减…………………………………10分
∵
∴方程在[1,2]上有唯一实数解
当时,;当时,
数学文试题
考试时间:120分钟 分值:150分
一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.若复数(为虚数单位),是的模,则的虚部是( )
A. B. C.1 D.
2.若集合A={直线},B={圆},则集合(A∩B)所含元素个数为( )
A.0或1或2 B.0 C.1 D.2
3.已知,则( )
A. B. C. D.
4.已知变量具有线性相关关系,测得的一组数据如下:,其回归方程为,则的值等于( )
A.0.9 B.0.8 C.0.6 D.0.2
5. “”是“”的 ( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
6.若,则的解集为( )
A. B.
C. D.
7.执行如图所示的程序框图,若输入,则输出的
( )
A. B. C. D.
8.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,该四棱锥表面积和体积分别是( )
A. B.
C. D.8,8
9.抛物线绕轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,使正方体的一个面恰好与旋转体的开口面平齐,则此正方体的棱长是( )
A.1 B.2 C.3 D.
10.已知函数(k≠0),定义函数
,给出下列命题:
①函数是奇函数;②;③当k<0,若mn<0,m+n<0,总有成立,其中所有正确命题的个数是( )
A.0 B.1 C.2 D.3
二.填空题:(本大题共5小题,每小题5分,共25分;把答案写在答题卷中对应题号的横线上。)
11.已知向量 ,若∥,则·=_______.
12.设等差数列、等比数列首项都是1,公差与公比都是2,则 .
13.已知函数是定义在R上的奇函数,若对于任意给定的不等实数x1,x2,不等式恒成立,则不等式的解集为 .
14.在平面直角坐标系XOY中,圆C的方程为,若直线上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的取值范围是 .
15.已知函数,等于抛掷一颗均匀的正六面体骰子得到的点数,则在上有偶数个零点的概率是 .
三、解答题:(本大题共6小题,共75分;写出必要的文字说明、证明过程或演算步骤)
16.(本小题满分12分)已知数列中,,(为数列的前n项和),数列为等差数列且满足,;
(1)求数列的通项公式;(2)设数列的前n项和为Tn,求Tn.
17.(本小题满分12分)在△中,内角,,的对边边长分别为,,,且.
(1)判断△的形状; (2)若,则△的面积是多少?
18.(本小题满分12分)通过随机调查九校高三100名学生在高二文理分科是否与性别有关,得到如下的列联表:(单位:人)
(1)从这50名女生中按文理采取分层抽样,抽取一个容量为5的样本,问样本中文科生与理科生各多少人?
(2)从(1)中抽到的5名女生中随机选取两名访谈,求选到文科生、理科生各一名的概率;
(3)根据以上列联表;问有多大把握认为“文理分科与性别”有关?
统计量,其中
概率表:
P(k2≥k0)
0.15
0.10
0.05
0.025
0.010
k0
2.072
2.706
3.841
5.024
6.635
19.(本小题满分12分)如图,在正四棱柱ABCD-A1B1C1D1中,已知底面ABCD边长为2,侧棱AA1=6.
(1)点P在侧棱AA1上,若AP=,求证:平面PBD⊥平面C1BD;
(2)求几何体BA1C1D的体积.
20.(本小题满分13分)已知椭圆C的中心在原点,焦点在轴上,离心率等于,它的一个顶点恰好是抛物线的焦点.
(1)求椭圆C的方程;
(2)、是椭圆上两点,A、B是椭圆位于直线PQ两侧的两动点,当A、B运动时,满足,试问直线AB的斜率是否为定值,请说明理由.
21.(本小题满分14分)已知,设函数 .
(1)求函数的单调区间;
(2)是否存在整数t,对于任意,关于x的方程在区间上有唯一实数解,若存在,求t的值;若不存在,说明理由.
江西省重点中学协作体2014届高三第一次联考数学(文)
参考答案
选择题(本大题共10小题,每小题5分,共50分)
二.填空题(本大题共5小题,每小题5分,共25分)
11. -10 12. 57 13. 14. 15.
三.简答题(共75分)
(2)由(1)知
∵为等差数列
∴其公差
∴
∴…………………………………9分
∴当时,
当时,
综上可知……………………………12分
17. 答案:(1)由得,
即,即,
所以或,
即或. ………………………………………………3分
因为,所以,即,所以不成立,舍去,
所以,即.所以△是直角三角形。……………………………6分
18.(1)文科生3人,理科生2人…………………………………………4分
(2)设三名文科生分别为文1、文2、文3,两名理科生分别为理1、理2、,则从中任选两人的结果为(文1,文2)、(文1,文3)、(文1,理1)、(文1,理2)、(文2,文3)、(文2,理1)、(文2,理2)、(文3,理1)、(文3,理2)、(理1,理2)共10种情况,其中一文一理的共6种。
∴…………………………………………8分
(3)
∴有99%的把握认为 “文理分科与性别”有关。……………………………………12分
19.(1)连结AC交BD于点O,连结C1O,PO
∵正四棱柱ABCD-A1B1C1D1
∴C1C⊥平面ABCD且O为BD、AC中点
∴C1C⊥CD C1C⊥BC
又∵正四棱柱ABCD-A1B1C1D1 ∴CD=CB ∴C1D=C1B ∴C1O⊥BD
又
∴C1O⊥OP ∵OP∩BD=0
又PO 平面PBD BD 平面PBD ∴C1O⊥平面 又∵C1O 平面C1BD
∴平面PBD⊥平面C1BD…………………………………………6分
…………………………………………12分
(2)∵,则PA、PB的斜率之和为0,设直线PA的斜率为,则PB的斜率为,
PA的直线方程为,设A(x1、y1),B(x2、y2)
由.将(1)代入(2)整理得,
有.同理PB的直线方程为,
可得,∴,.
从而====,
所以的斜率为定值.………………………………………………13分
故函数在R上单调递减
当时,方程的两个实根为
则时,;时,,时,
故函数的单调递减区间为、
单调递增区间为…………………………………6分
1)当时,,解得
∴关于x的方程有唯一实数解
∴,故在上单调递减…………………………………10分
∵
∴方程在[1,2]上有唯一实数解
当时,;当时,
同课章节目录
