5.1.1 相交线 同步练习(含答案)
图片预览




文档简介
5.1 相交线
第1课时 相交线
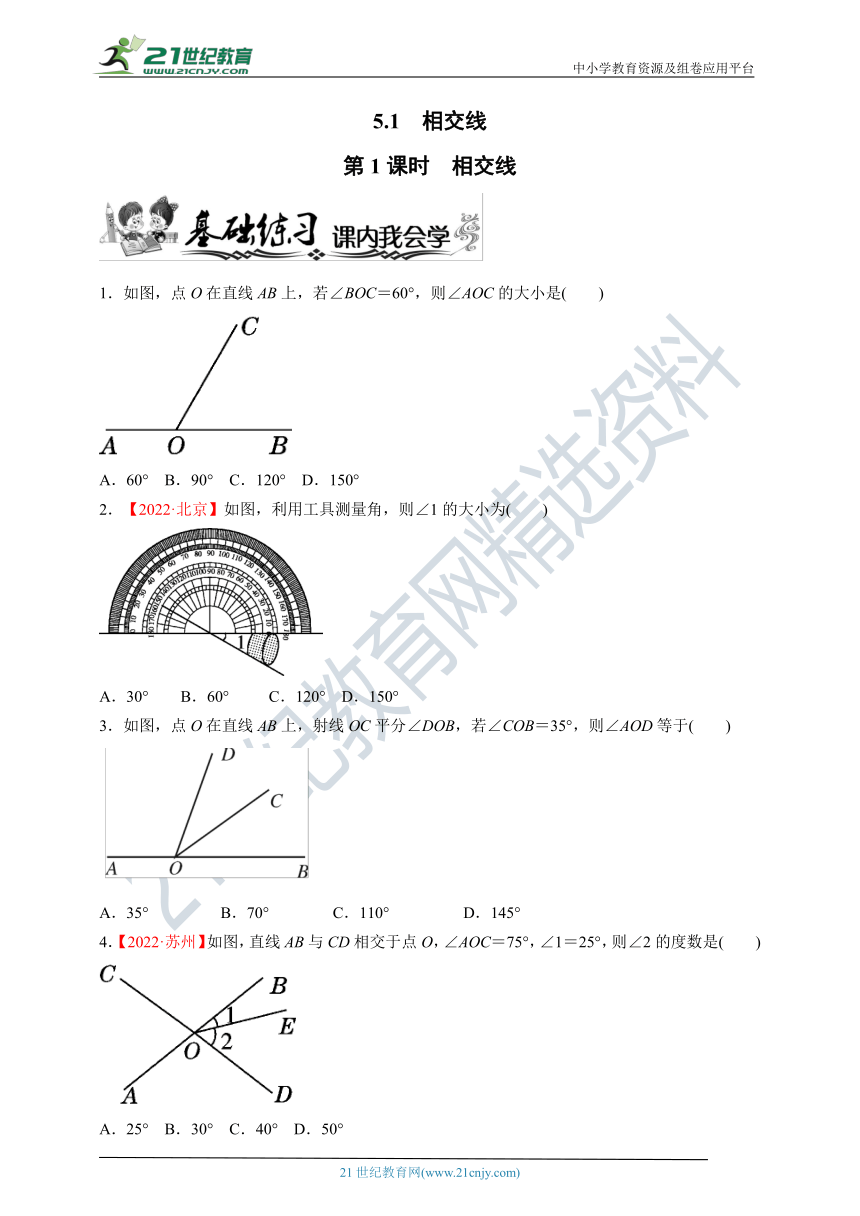
1.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
A.60° B.90° C.120° D.150°
2.【2022·北京】如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
3.如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
4.【2022·苏州】如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
5.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
6.已知∠1的对顶角为132°,则∠1的邻补角度数为 .
7.如图,直线AB、CD相交于点O.
(1)若∠AOD比∠AOC大40°,求∠BOD的度数;
(2)若∠AOD=2∠AOC,求∠BOC的度数;
(3)若∠AOD∶∠AOC=3∶2,求∠BOD的度数.
8.下列图形中,∠1与∠2是对顶角的是( )
9.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A.20° B.25° C.30° D.70°
10.【福州中考】如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( )
A.20° B.40° C.50° D.80°
11.【2021·益阳】如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD=________度.
12.对顶角是成对出现的,其位置关系为:
(1)_______________;
(2)_________________________________________.
其数量关系为__________.
互为对顶角的两个角相等,但相等的两个角不一定是对顶角.
13.如图,直线AB与直线CD相交于点O.
(1)若∠1+∠3=110°,则∠3= ;
(2)若∠2=2∠1,则∠3= ;
(3)若∠2-∠1=20°,则∠3= .
14.如图,已知直线AB,CD相交于点O,且OE平分∠BOC.
(1)∠AOC与________________互为邻补角.
(2)与∠EOA互为补角的是哪些角?试说明理由.
(3)若∠AOC=42°,求∠BOE的度数.
15.【逻辑推理】如图,O是直线AB上一点,OD平分∠AOC,OE平分∠BOC.
(1)图中∠BOD的邻补角为________,∠AOE的邻补角为________.
(2)①如果∠COD=25°,求∠BOE的度数;
②如果∠COD=60°,求∠BOE的度数.
16.【2022·贵阳实验二中模拟】如图,直线AB,CD, EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
(2)通过求∠AOF的度数,你能发现射线OA有什么特殊性吗?
17.如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=50°,求∠DOF,∠DOE和∠EOF的度数.
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求出其值;若变化,说明理由.
18.我们知道,两条直线相交,一共有两对对顶角,那么三条直线、四条直线、甚至是n条直线相交于一点或两两相交,有几组对顶角呢?请思考如下问题:
(1)如图,数一数下列各个图形中对顶角的组数:
图①: 组, 组;图②: 组, 组;
(2)两条直线相交,最多有 个交点,三条直线相交,最多有 个交点;四条直线相交,最多有 个交点;依次类推,n条直线相交,最多有 个交点;
(3)由于对顶角是两条直线相交而构成的,每个交点有两组对顶角,因此可知对顶角的组数为直线交点个数的2倍,结合(1)、(2)可发现结论:n条直线相交于一点,共有 组对顶角.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( C )
A.60° B.90° C.120° D.150°
2.【2022·北京】如图,利用工具测量角,则∠1的大小为( A )
A.30° B.60° C.120° D.150°
3.如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD等于( C )
A.35° B.70° C.110° D.145°
4.【2022·苏州】如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( D )
A.25° B.30° C.40° D.50°
5.如图,三条直线相交于点O,则∠1+∠2+∠3等于( C )
A.90° B.120° C.180° D.360°
6.已知∠1的对顶角为132°,则∠1的邻补角度数为 .
【答案】48°
7.如图,直线AB、CD相交于点O.
(1)若∠AOD比∠AOC大40°,求∠BOD的度数;
(2)若∠AOD=2∠AOC,求∠BOC的度数;
(3)若∠AOD∶∠AOC=3∶2,求∠BOD的度数.
解:(1)设∠AOC=x,则∠AOD=x+40°.∵x+(x+40°)=180°,∴x=70°,∴∠BOD=∠AOC=70°;
(2)设∠AOC=x,则∠AOD=2x,∴x+2x=180°,∴x=60°,∴∠BOC=180°-∠AOC=120°;
(3)设∠AOD=3x,则∠AOC=2x,∴3x+2x=180°,∴x=36°,∴∠AOC=72°,∴∠BOD=72°.
8.下列图形中,∠1与∠2是对顶角的是( C )
9.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( D )
A.20° B.25° C.30° D.70°
10.【福州中考】如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( C )
A.20° B.40° C.50° D.80°
11.【2021·益阳】如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD=________度.
【答案】60
12.对顶角是成对出现的,其位置关系为:
(1)_______________;
(2)_________________________________________.
其数量关系为__________.
互为对顶角的两个角相等,但相等的两个角不一定是对顶角.
【答案】有公共顶点 两个角的两边分别互为反向延长线 相等
13.如图,直线AB与直线CD相交于点O.
(1)若∠1+∠3=110°,则∠3= ;
(2)若∠2=2∠1,则∠3= ;
(3)若∠2-∠1=20°,则∠3= .
【答案】55° 60° 80°
14.如图,已知直线AB,CD相交于点O,且OE平分∠BOC.
(1)∠AOC与________________互为邻补角.
【答案】∠BOC,∠AOD
(2)与∠EOA互为补角的是哪些角?试说明理由.
与∠EOA互为补角的角是∠EOB,∠COE.
理由:因为∠EOA+∠EOB=180°,
所以∠EOA与∠EOB互为补角.因为OE平分∠BOC,
所以∠COE=∠EOB.所以∠EOA+∠COE=180°.
所以∠EOA与∠COE互为补角.
(3)若∠AOC=42°,求∠BOE的度数.
因为∠AOC=42°,而∠AOC+∠BOC=180°,
所以∠BOC=180°-42°=138°.
又因为OE平分∠BOC,
所以∠BOE=∠BOC=×138°=69°.
15.【逻辑推理】如图,O是直线AB上一点,OD平分∠AOC,OE平分∠BOC.
(1)图中∠BOD的邻补角为________,∠AOE的邻补角为________.
【答案】∠AOD ∠BOE
(2)①如果∠COD=25°,求∠BOE的度数;
因为OD平分∠AOC,OE平分∠BOC,
所以∠COD=∠AOC,∠BOE=∠BOC.
因为∠COD=25°,所以∠AOC=2×25°=50°.
所以∠BOC=180°-50°=130°.所以∠BOE=∠BOC=65°.
②如果∠COD=60°,求∠BOE的度数.
因为OD平分∠AOC,OE平分∠BOC,
所以∠COD=∠AOC,∠BOE=∠BOC.
因为∠COD=60°,所以∠AOC=120°.
所以∠BOC=180°-120°=60°.
所以∠BOE=∠BOC=30°.
16.【2022·贵阳实验二中模拟】如图,直线AB,CD, EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
解:(1)因为∠AOC=65°,
所以∠BOD=∠AOC=65°.
又因为∠BOE+∠BOD+∠DOF=180°,∠DOF=50°,
所以∠BOE=180°-65°-50°=65°.
(2)通过求∠AOF的度数,你能发现射线OA有什么特殊性吗?
因为∠AOF=∠BOE=65°,且∠AOC=65°,
所以∠AOF=∠AOC.
所以射线OA是∠COF的平分线.
17.如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=50°,求∠DOF,∠DOE和∠EOF的度数.
解:(1)由对顶角相等得∠BOD=∠AOC=50° .
因为OF平分∠BOD,
所以∠DOF=∠BOD=×50° =25° .
因为OE平分∠AOD,∠AOD=180° -∠AOC=
180° -50° =130° ,
所以∠DOE=∠AOD=×130° =65° .
所以∠EOF=∠DOF+∠DOE=25°+65°=90°.
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求出其值;若变化,说明理由.
当∠AOC的度数变化时,∠EOF的度数不变.
因为OF平分∠BOD,所以∠DOF=∠BOD.
因为OE平分∠AOD,所以∠DOE=∠AOD.
所以∠EOF=∠DOF+∠DOE=∠BOD+∠AOD=(∠BOD+∠AOD)=∠AOB=90°.
18.我们知道,两条直线相交,一共有两对对顶角,那么三条直线、四条直线、甚至是n条直线相交于一点或两两相交,有几组对顶角呢?请思考如下问题:
(1)如图,数一数下列各个图形中对顶角的组数:
图①: 组, 组;图②: 组, 组;
【答案】6 6 12 12
(2)两条直线相交,最多有 个交点,三条直线相交,最多有 个交点;四条直线相交,最多有 个交点;依次类推,n条直线相交,最多有 个交点;
【答案】1 3 6
(3)由于对顶角是两条直线相交而构成的,每个交点有两组对顶角,因此可知对顶角的组数为直线交点个数的2倍,结合(1)、(2)可发现结论:n条直线相交于一点,共有 组对顶角.
【答案】n(n-1)
第1课时 相交线
1.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
A.60° B.90° C.120° D.150°
2.【2022·北京】如图,利用工具测量角,则∠1的大小为( )
A.30° B.60° C.120° D.150°
3.如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD等于( )
A.35° B.70° C.110° D.145°
4.【2022·苏州】如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( )
A.25° B.30° C.40° D.50°
5.如图,三条直线相交于点O,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
6.已知∠1的对顶角为132°,则∠1的邻补角度数为 .
7.如图,直线AB、CD相交于点O.
(1)若∠AOD比∠AOC大40°,求∠BOD的度数;
(2)若∠AOD=2∠AOC,求∠BOC的度数;
(3)若∠AOD∶∠AOC=3∶2,求∠BOD的度数.
8.下列图形中,∠1与∠2是对顶角的是( )
9.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( )
A.20° B.25° C.30° D.70°
10.【福州中考】如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( )
A.20° B.40° C.50° D.80°
11.【2021·益阳】如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD=________度.
12.对顶角是成对出现的,其位置关系为:
(1)_______________;
(2)_________________________________________.
其数量关系为__________.
互为对顶角的两个角相等,但相等的两个角不一定是对顶角.
13.如图,直线AB与直线CD相交于点O.
(1)若∠1+∠3=110°,则∠3= ;
(2)若∠2=2∠1,则∠3= ;
(3)若∠2-∠1=20°,则∠3= .
14.如图,已知直线AB,CD相交于点O,且OE平分∠BOC.
(1)∠AOC与________________互为邻补角.
(2)与∠EOA互为补角的是哪些角?试说明理由.
(3)若∠AOC=42°,求∠BOE的度数.
15.【逻辑推理】如图,O是直线AB上一点,OD平分∠AOC,OE平分∠BOC.
(1)图中∠BOD的邻补角为________,∠AOE的邻补角为________.
(2)①如果∠COD=25°,求∠BOE的度数;
②如果∠COD=60°,求∠BOE的度数.
16.【2022·贵阳实验二中模拟】如图,直线AB,CD, EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
(2)通过求∠AOF的度数,你能发现射线OA有什么特殊性吗?
17.如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=50°,求∠DOF,∠DOE和∠EOF的度数.
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求出其值;若变化,说明理由.
18.我们知道,两条直线相交,一共有两对对顶角,那么三条直线、四条直线、甚至是n条直线相交于一点或两两相交,有几组对顶角呢?请思考如下问题:
(1)如图,数一数下列各个图形中对顶角的组数:
图①: 组, 组;图②: 组, 组;
(2)两条直线相交,最多有 个交点,三条直线相交,最多有 个交点;四条直线相交,最多有 个交点;依次类推,n条直线相交,最多有 个交点;
(3)由于对顶角是两条直线相交而构成的,每个交点有两组对顶角,因此可知对顶角的组数为直线交点个数的2倍,结合(1)、(2)可发现结论:n条直线相交于一点,共有 组对顶角.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( C )
A.60° B.90° C.120° D.150°
2.【2022·北京】如图,利用工具测量角,则∠1的大小为( A )
A.30° B.60° C.120° D.150°
3.如图,点O在直线AB上,射线OC平分∠DOB,若∠COB=35°,则∠AOD等于( C )
A.35° B.70° C.110° D.145°
4.【2022·苏州】如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是( D )
A.25° B.30° C.40° D.50°
5.如图,三条直线相交于点O,则∠1+∠2+∠3等于( C )
A.90° B.120° C.180° D.360°
6.已知∠1的对顶角为132°,则∠1的邻补角度数为 .
【答案】48°
7.如图,直线AB、CD相交于点O.
(1)若∠AOD比∠AOC大40°,求∠BOD的度数;
(2)若∠AOD=2∠AOC,求∠BOC的度数;
(3)若∠AOD∶∠AOC=3∶2,求∠BOD的度数.
解:(1)设∠AOC=x,则∠AOD=x+40°.∵x+(x+40°)=180°,∴x=70°,∴∠BOD=∠AOC=70°;
(2)设∠AOC=x,则∠AOD=2x,∴x+2x=180°,∴x=60°,∴∠BOC=180°-∠AOC=120°;
(3)设∠AOD=3x,则∠AOC=2x,∴3x+2x=180°,∴x=36°,∴∠AOC=72°,∴∠BOD=72°.
8.下列图形中,∠1与∠2是对顶角的是( C )
9.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是( D )
A.20° B.25° C.30° D.70°
10.【福州中考】如图,已知直线AB、CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是( C )
A.20° B.40° C.50° D.80°
11.【2021·益阳】如图,AB与CD相交于点O,OE是∠AOC的平分线,且OC恰好平分∠EOB,则∠AOD=________度.
【答案】60
12.对顶角是成对出现的,其位置关系为:
(1)_______________;
(2)_________________________________________.
其数量关系为__________.
互为对顶角的两个角相等,但相等的两个角不一定是对顶角.
【答案】有公共顶点 两个角的两边分别互为反向延长线 相等
13.如图,直线AB与直线CD相交于点O.
(1)若∠1+∠3=110°,则∠3= ;
(2)若∠2=2∠1,则∠3= ;
(3)若∠2-∠1=20°,则∠3= .
【答案】55° 60° 80°
14.如图,已知直线AB,CD相交于点O,且OE平分∠BOC.
(1)∠AOC与________________互为邻补角.
【答案】∠BOC,∠AOD
(2)与∠EOA互为补角的是哪些角?试说明理由.
与∠EOA互为补角的角是∠EOB,∠COE.
理由:因为∠EOA+∠EOB=180°,
所以∠EOA与∠EOB互为补角.因为OE平分∠BOC,
所以∠COE=∠EOB.所以∠EOA+∠COE=180°.
所以∠EOA与∠COE互为补角.
(3)若∠AOC=42°,求∠BOE的度数.
因为∠AOC=42°,而∠AOC+∠BOC=180°,
所以∠BOC=180°-42°=138°.
又因为OE平分∠BOC,
所以∠BOE=∠BOC=×138°=69°.
15.【逻辑推理】如图,O是直线AB上一点,OD平分∠AOC,OE平分∠BOC.
(1)图中∠BOD的邻补角为________,∠AOE的邻补角为________.
【答案】∠AOD ∠BOE
(2)①如果∠COD=25°,求∠BOE的度数;
因为OD平分∠AOC,OE平分∠BOC,
所以∠COD=∠AOC,∠BOE=∠BOC.
因为∠COD=25°,所以∠AOC=2×25°=50°.
所以∠BOC=180°-50°=130°.所以∠BOE=∠BOC=65°.
②如果∠COD=60°,求∠BOE的度数.
因为OD平分∠AOC,OE平分∠BOC,
所以∠COD=∠AOC,∠BOE=∠BOC.
因为∠COD=60°,所以∠AOC=120°.
所以∠BOC=180°-120°=60°.
所以∠BOE=∠BOC=30°.
16.【2022·贵阳实验二中模拟】如图,直线AB,CD, EF相交于点O,如果∠AOC=65°,∠DOF=50°.
(1)求∠BOE的度数;
解:(1)因为∠AOC=65°,
所以∠BOD=∠AOC=65°.
又因为∠BOE+∠BOD+∠DOF=180°,∠DOF=50°,
所以∠BOE=180°-65°-50°=65°.
(2)通过求∠AOF的度数,你能发现射线OA有什么特殊性吗?
因为∠AOF=∠BOE=65°,且∠AOC=65°,
所以∠AOF=∠AOC.
所以射线OA是∠COF的平分线.
17.如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.
(1)若∠AOC=50°,求∠DOF,∠DOE和∠EOF的度数.
解:(1)由对顶角相等得∠BOD=∠AOC=50° .
因为OF平分∠BOD,
所以∠DOF=∠BOD=×50° =25° .
因为OE平分∠AOD,∠AOD=180° -∠AOC=
180° -50° =130° ,
所以∠DOE=∠AOD=×130° =65° .
所以∠EOF=∠DOF+∠DOE=25°+65°=90°.
(2)当∠AOC的度数变化时,∠EOF的度数是否变化?若不变,求出其值;若变化,说明理由.
当∠AOC的度数变化时,∠EOF的度数不变.
因为OF平分∠BOD,所以∠DOF=∠BOD.
因为OE平分∠AOD,所以∠DOE=∠AOD.
所以∠EOF=∠DOF+∠DOE=∠BOD+∠AOD=(∠BOD+∠AOD)=∠AOB=90°.
18.我们知道,两条直线相交,一共有两对对顶角,那么三条直线、四条直线、甚至是n条直线相交于一点或两两相交,有几组对顶角呢?请思考如下问题:
(1)如图,数一数下列各个图形中对顶角的组数:
图①: 组, 组;图②: 组, 组;
【答案】6 6 12 12
(2)两条直线相交,最多有 个交点,三条直线相交,最多有 个交点;四条直线相交,最多有 个交点;依次类推,n条直线相交,最多有 个交点;
【答案】1 3 6
(3)由于对顶角是两条直线相交而构成的,每个交点有两组对顶角,因此可知对顶角的组数为直线交点个数的2倍,结合(1)、(2)可发现结论:n条直线相交于一点,共有 组对顶角.
【答案】n(n-1)
