5.1.3 同位角、内错角、同旁内角 同步练习(含答案)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 09:58:07 | ||
图片预览





文档简介
5.1 相交线
第3课时 同位角、内错角、同旁内角
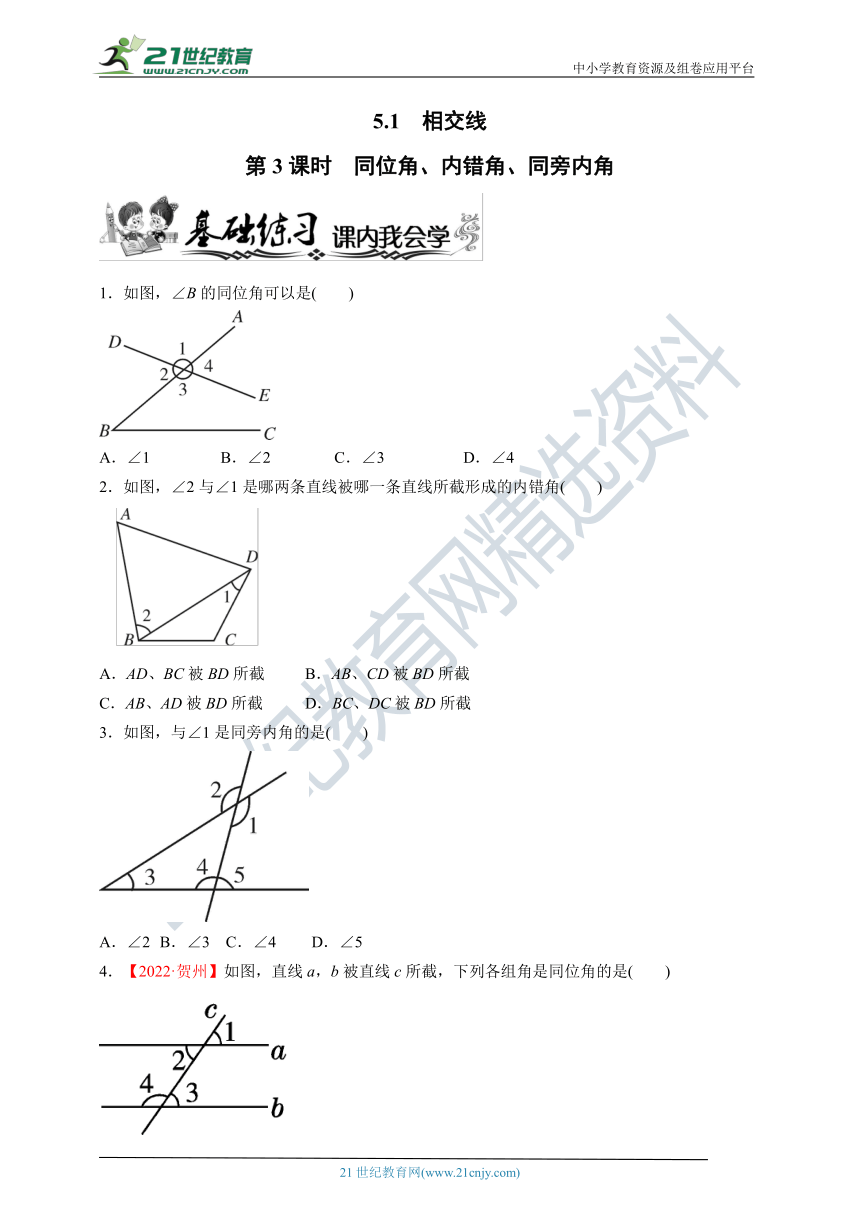
1.如图,∠B的同位角可以是( )
A.∠1 B.∠2 C.∠3 D.∠4
2.如图,∠2与∠1是哪两条直线被哪一条直线所截形成的内错角( )
A.AD、BC被BD所截 B.AB、CD被BD所截
C.AB、AD被BD所截 D.BC、DC被BD所截
3.如图,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.【2022·贺州】如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.∠1与∠2 B.∠1与∠3
C.∠2与∠3 D.∠3与∠4
5.【2021 百色】如图,与∠1是内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
6.【2021 贺州】如图,下列两个角是同旁内角的是( )
A.∠1与∠2 B.∠1与∠3 C.∠1与∠4 D.∠2与∠4
7.(1)两条直线被第三条直线所截,位于截线的同侧,且分别在被截线同一方的两个角,叫 .
(2)两条直线被第三条直线所截,位于截线的两侧,且都在被截线之间的两个角,叫 .
(3)两条直线被第三条直线所截,位于截线的同旁且都在被截线之间的两个角,叫 .
8.如图,图①中∠1和∠2、∠3和∠4分别是由哪两条直线被哪一条直线所截而成的?图②中它们各是什么角?
9.如图所示,∠1~∠8这8个角中,同位角、内错角、同旁内角各有几对?请分别写出来.
10.如图,直线a、b被直线c所截,∠1与∠2的位置关系是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
11.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( )
A.∠1 B.∠2 C.∠4 D.∠5
12.下图中,∠1与∠2是同位角的是( )
13.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( )
14.如图,与∠B是同旁内角的角有( )
A.1个 B.2个 C.3个 D.4个
15.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ,内错角是 ,同旁内角是 .
16.如图,∠B与∠1是两条直线 和 被直线 所截得到的一对 角;∠2和∠4是两条直线 和 被直线 所截得到的一对 角;∠ACB和∠3是两条直线 和 被第三条直线 所截得到的一对 角.
17.如图,标有角号的7个角中与∠1是内错角、同旁内角的各有哪几个 与∠5是同位角的有哪几个
18.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2的度数.
19.如图,直线DE和BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么位置关系的角?
(2)∠1与∠5是内错角吗?为什么?
(3)如果∠1+∠3=180°,那么∠1等于∠2吗?∠1和∠5互补吗?为什么?
20.已知直线AB、CD被EF所截,点G、H为它们的交点,∠1∶∠2=5∶3,∠2与它的内错角相等,HP平分∠CHG.求:
(1)∠4的度数;
(2)∠GHP的度数.
21.【规律探索题】探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,∠B的同位角可以是( D )
A.∠1 B.∠2 C.∠3 D.∠4
2.如图,∠2与∠1是哪两条直线被哪一条直线所截形成的内错角( B )
A.AD、BC被BD所截 B.AB、CD被BD所截
C.AB、AD被BD所截 D.BC、DC被BD所截
3.如图,与∠1是同旁内角的是( D )
A.∠2 B.∠3 C.∠4 D.∠5
4.【2022·贺州】如图,直线a,b被直线c所截,下列各组角是同位角的是( B )
A.∠1与∠2 B.∠1与∠3
C.∠2与∠3 D.∠3与∠4
5.【2021 百色】如图,与∠1是内错角的是( C )
A.∠2 B.∠3 C.∠4 D.∠5
6.【2021 贺州】如图,下列两个角是同旁内角的是( B )
A.∠1与∠2 B.∠1与∠3 C.∠1与∠4 D.∠2与∠4
7.(1)两条直线被第三条直线所截,位于截线的同侧,且分别在被截线同一方的两个角,叫 .
【答案】同位角
(2)两条直线被第三条直线所截,位于截线的两侧,且都在被截线之间的两个角,叫 .
【答案】内错角
(3)两条直线被第三条直线所截,位于截线的同旁且都在被截线之间的两个角,叫 .
【答案】同旁内角
8.如图,图①中∠1和∠2、∠3和∠4分别是由哪两条直线被哪一条直线所截而成的?图②中它们各是什么角?
解:图①中,∠1和∠2是直线AB与CD被直线BD所截形成的内错角,∠3和∠4是直线AD与BC被直线BD所截形成的内错角.图②中,∠1和∠2是直线AB与CD被直线BC所截形成的同位角,∠3和∠4是直线AB与BC被直线AC所截形成的同旁内角.
9.如图所示,∠1~∠8这8个角中,同位角、内错角、同旁内角各有几对?请分别写出来.
【规范解答】 同位角有2对:∠1与∠3,∠5与∠8;内错角有4对:∠1与∠7,∠2与∠8,∠3与∠6,∠4与∠7;同旁内角有7对:∠1与∠8,∠2与∠3,∠2与∠7,∠3与∠7,∠4与∠5,∠4与∠6,∠5与∠6.
10.如图,直线a、b被直线c所截,∠1与∠2的位置关系是( B )
A.同位角 B.内错角 C.同旁内角 D.对顶角
11.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( B )
A.∠1 B.∠2 C.∠4 D.∠5
12.下图中,∠1与∠2是同位角的是( D )
13.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( C )
14.如图,与∠B是同旁内角的角有( C )
A.1个 B.2个 C.3个 D.4个
15.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ∠1与∠B,∠4与∠B ,内错角是 ∠2与∠5,∠3与∠4 ,同旁内角是 ∠B和∠3,∠B和∠5,∠2与∠4,∠3与∠5 .
16.如图,∠B与∠1是两条直线 DE 和 BC 被直线 AB 所截得到的一对 同位 角;∠2和∠4是两条直线 DE 和 BC 被直线 DC 所截得到的一对 内错 角;∠ACB和∠3是两条直线 DE 和 BC 被第三条直线 AC 所截得到的一对 同旁内 角.
17.如图,标有角号的7个角中与∠1是内错角、同旁内角的各有哪几个 与∠5是同位角的有哪几个
解:与∠1是内错角的有∠4、∠7两个,与∠1是同旁内角的有∠6、∠5两个,与∠5是同位角的只有∠7一个.
18.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图;
解:(1)如答图所示.(画法不唯一)
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2的度数.
因为∠1=2∠2,∠2=2∠3,所以∠1=4∠3.
又因为∠1+∠3=180°,所以4∠3+∠3=180°.
所以∠3=36°.所以∠2=72°,∠1=144°.
19.如图,直线DE和BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么位置关系的角?
解:(1)∠1与∠2是内错角,∠1与∠3是同旁内角,
∠1与∠4是同位角.
(2)∠1与∠5是内错角吗?为什么?
∠1与∠5不是内错角,因为内错角必须在两条被截直线之间.
(3)如果∠1+∠3=180°,那么∠1等于∠2吗?∠1和∠5互补吗?为什么?
∠1=∠2,∠1和∠5互补.
理由:因为∠1+∠3=180°,∠3+∠2=180°,
所以∠1=∠2.
因为∠1和∠3互补,∠3=∠5,
所以∠1和∠5也互补.
20.已知直线AB、CD被EF所截,点G、H为它们的交点,∠1∶∠2=5∶3,∠2与它的内错角相等,HP平分∠CHG.求:
(1)∠4的度数;
(2)∠GHP的度数.
解:(1)∵∠1与∠2互补,∴∠1+∠2=180°.又∠1∶∠2=5∶3,∴∠1=112.5°,∠2=67.5°.又∵∠2与它的内错角∠4相等,∴∠4=67.5°;
(2)∵∠4与∠CHG互补,∴∠CHG=180°-∠4=112.5°.又HP平分∠CHG,∴∠GHP=∠CHG=56.25°.
21.【规律探索题】探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
【答案】4 2 2
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
【答案】12 6 6
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
【答案】2n(n-1) n(n-1) n(n-1)
【思路点拨】(1)要求同位角、内错角和同旁内角的对数,图①中的图形是“三线八角”的基本图形,所以容易得出;
(2)把图②中的图形进行拆分得3个“三线八角”的基本图形,即可求出;
(3)当有n条水平直线时,可以拆分成个“三线八角”的基本图形,从而得出规律.
【点规律】本题中的规律也可以这样总结:当n条水平直线被一条竖直直线所截时,内错角和同旁内角各有n(n-1)对,而同位角的对数是内错角的对数的2倍,因此有2n(n-1)对
第3课时 同位角、内错角、同旁内角
1.如图,∠B的同位角可以是( )
A.∠1 B.∠2 C.∠3 D.∠4
2.如图,∠2与∠1是哪两条直线被哪一条直线所截形成的内错角( )
A.AD、BC被BD所截 B.AB、CD被BD所截
C.AB、AD被BD所截 D.BC、DC被BD所截
3.如图,与∠1是同旁内角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
4.【2022·贺州】如图,直线a,b被直线c所截,下列各组角是同位角的是( )
A.∠1与∠2 B.∠1与∠3
C.∠2与∠3 D.∠3与∠4
5.【2021 百色】如图,与∠1是内错角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
6.【2021 贺州】如图,下列两个角是同旁内角的是( )
A.∠1与∠2 B.∠1与∠3 C.∠1与∠4 D.∠2与∠4
7.(1)两条直线被第三条直线所截,位于截线的同侧,且分别在被截线同一方的两个角,叫 .
(2)两条直线被第三条直线所截,位于截线的两侧,且都在被截线之间的两个角,叫 .
(3)两条直线被第三条直线所截,位于截线的同旁且都在被截线之间的两个角,叫 .
8.如图,图①中∠1和∠2、∠3和∠4分别是由哪两条直线被哪一条直线所截而成的?图②中它们各是什么角?
9.如图所示,∠1~∠8这8个角中,同位角、内错角、同旁内角各有几对?请分别写出来.
10.如图,直线a、b被直线c所截,∠1与∠2的位置关系是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
11.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( )
A.∠1 B.∠2 C.∠4 D.∠5
12.下图中,∠1与∠2是同位角的是( )
13.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( )
14.如图,与∠B是同旁内角的角有( )
A.1个 B.2个 C.3个 D.4个
15.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ,内错角是 ,同旁内角是 .
16.如图,∠B与∠1是两条直线 和 被直线 所截得到的一对 角;∠2和∠4是两条直线 和 被直线 所截得到的一对 角;∠ACB和∠3是两条直线 和 被第三条直线 所截得到的一对 角.
17.如图,标有角号的7个角中与∠1是内错角、同旁内角的各有哪几个 与∠5是同位角的有哪几个
18.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2的度数.
19.如图,直线DE和BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么位置关系的角?
(2)∠1与∠5是内错角吗?为什么?
(3)如果∠1+∠3=180°,那么∠1等于∠2吗?∠1和∠5互补吗?为什么?
20.已知直线AB、CD被EF所截,点G、H为它们的交点,∠1∶∠2=5∶3,∠2与它的内错角相等,HP平分∠CHG.求:
(1)∠4的度数;
(2)∠GHP的度数.
21.【规律探索题】探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,∠B的同位角可以是( D )
A.∠1 B.∠2 C.∠3 D.∠4
2.如图,∠2与∠1是哪两条直线被哪一条直线所截形成的内错角( B )
A.AD、BC被BD所截 B.AB、CD被BD所截
C.AB、AD被BD所截 D.BC、DC被BD所截
3.如图,与∠1是同旁内角的是( D )
A.∠2 B.∠3 C.∠4 D.∠5
4.【2022·贺州】如图,直线a,b被直线c所截,下列各组角是同位角的是( B )
A.∠1与∠2 B.∠1与∠3
C.∠2与∠3 D.∠3与∠4
5.【2021 百色】如图,与∠1是内错角的是( C )
A.∠2 B.∠3 C.∠4 D.∠5
6.【2021 贺州】如图,下列两个角是同旁内角的是( B )
A.∠1与∠2 B.∠1与∠3 C.∠1与∠4 D.∠2与∠4
7.(1)两条直线被第三条直线所截,位于截线的同侧,且分别在被截线同一方的两个角,叫 .
【答案】同位角
(2)两条直线被第三条直线所截,位于截线的两侧,且都在被截线之间的两个角,叫 .
【答案】内错角
(3)两条直线被第三条直线所截,位于截线的同旁且都在被截线之间的两个角,叫 .
【答案】同旁内角
8.如图,图①中∠1和∠2、∠3和∠4分别是由哪两条直线被哪一条直线所截而成的?图②中它们各是什么角?
解:图①中,∠1和∠2是直线AB与CD被直线BD所截形成的内错角,∠3和∠4是直线AD与BC被直线BD所截形成的内错角.图②中,∠1和∠2是直线AB与CD被直线BC所截形成的同位角,∠3和∠4是直线AB与BC被直线AC所截形成的同旁内角.
9.如图所示,∠1~∠8这8个角中,同位角、内错角、同旁内角各有几对?请分别写出来.
【规范解答】 同位角有2对:∠1与∠3,∠5与∠8;内错角有4对:∠1与∠7,∠2与∠8,∠3与∠6,∠4与∠7;同旁内角有7对:∠1与∠8,∠2与∠3,∠2与∠7,∠3与∠7,∠4与∠5,∠4与∠6,∠5与∠6.
10.如图,直线a、b被直线c所截,∠1与∠2的位置关系是( B )
A.同位角 B.内错角 C.同旁内角 D.对顶角
11.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( B )
A.∠1 B.∠2 C.∠4 D.∠5
12.下图中,∠1与∠2是同位角的是( D )
13.在我们常见的英文字母中,也存在着同位角、内错角、同旁内角.在下面几个字母中,含有内错角最少的字母是( C )
14.如图,与∠B是同旁内角的角有( C )
A.1个 B.2个 C.3个 D.4个
15.如图,在∠1、∠2、∠3、∠4、∠5和∠B中,同位角是 ∠1与∠B,∠4与∠B ,内错角是 ∠2与∠5,∠3与∠4 ,同旁内角是 ∠B和∠3,∠B和∠5,∠2与∠4,∠3与∠5 .
16.如图,∠B与∠1是两条直线 DE 和 BC 被直线 AB 所截得到的一对 同位 角;∠2和∠4是两条直线 DE 和 BC 被直线 DC 所截得到的一对 内错 角;∠ACB和∠3是两条直线 DE 和 BC 被第三条直线 AC 所截得到的一对 同旁内 角.
17.如图,标有角号的7个角中与∠1是内错角、同旁内角的各有哪几个 与∠5是同位角的有哪几个
解:与∠1是内错角的有∠4、∠7两个,与∠1是同旁内角的有∠6、∠5两个,与∠5是同位角的只有∠7一个.
18.两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.
(1)画出示意图;
解:(1)如答图所示.(画法不唯一)
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2的度数.
因为∠1=2∠2,∠2=2∠3,所以∠1=4∠3.
又因为∠1+∠3=180°,所以4∠3+∠3=180°.
所以∠3=36°.所以∠2=72°,∠1=144°.
19.如图,直线DE和BC被直线AB所截.
(1)∠1与∠2,∠1与∠3,∠1与∠4各是什么位置关系的角?
解:(1)∠1与∠2是内错角,∠1与∠3是同旁内角,
∠1与∠4是同位角.
(2)∠1与∠5是内错角吗?为什么?
∠1与∠5不是内错角,因为内错角必须在两条被截直线之间.
(3)如果∠1+∠3=180°,那么∠1等于∠2吗?∠1和∠5互补吗?为什么?
∠1=∠2,∠1和∠5互补.
理由:因为∠1+∠3=180°,∠3+∠2=180°,
所以∠1=∠2.
因为∠1和∠3互补,∠3=∠5,
所以∠1和∠5也互补.
20.已知直线AB、CD被EF所截,点G、H为它们的交点,∠1∶∠2=5∶3,∠2与它的内错角相等,HP平分∠CHG.求:
(1)∠4的度数;
(2)∠GHP的度数.
解:(1)∵∠1与∠2互补,∴∠1+∠2=180°.又∠1∶∠2=5∶3,∴∠1=112.5°,∠2=67.5°.又∵∠2与它的内错角∠4相等,∴∠4=67.5°;
(2)∵∠4与∠CHG互补,∴∠CHG=180°-∠4=112.5°.又HP平分∠CHG,∴∠GHP=∠CHG=56.25°.
21.【规律探索题】探究题:
(1)如图①,两条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,同旁内角有______对;
【答案】4 2 2
(2)如图②,三条水平的直线被一条竖直的直线所截,同位角有______对,内错角有______对,
同旁内角有______对;
【答案】12 6 6
(3)根据以上探究的结果,n(n为大于1的整数)条水平直线被一条竖直直线所截,同位角有________对,内错角有________对,同旁内角有________对.(用含n的式子表示)
【答案】2n(n-1) n(n-1) n(n-1)
【思路点拨】(1)要求同位角、内错角和同旁内角的对数,图①中的图形是“三线八角”的基本图形,所以容易得出;
(2)把图②中的图形进行拆分得3个“三线八角”的基本图形,即可求出;
(3)当有n条水平直线时,可以拆分成个“三线八角”的基本图形,从而得出规律.
【点规律】本题中的规律也可以这样总结:当n条水平直线被一条竖直直线所截时,内错角和同旁内角各有n(n-1)对,而同位角的对数是内错角的对数的2倍,因此有2n(n-1)对
