5.2.1 平行线 同步练习(含答案)
图片预览



文档简介
5.2 平行线及其判定
5.2.1 平行线
1.下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
2.下列表示方法正确的是( )
A.a∥A B.AB∥cd C.A∥B D.a∥b
3.如果线段AB与线段CD没有交点,则( )
A.线段AB与线段CD一定平行
B.线段AB与线段CD一定不平行
C.线段AB与线段CD可能平行
D.以上说法都不正确
4.如图,能相交的是 ,平行的是 .
5.(1)同一平面内 的两条直线,叫做平行线.平行线用“ ”符号表示,读作 .
(2)过直线外一点 一条直线与这条直线平行.平行于同一条直线的两条直线 .
(3)说明三点共线的方法,一是计算夹角为 ;二是说明过两点确定的两条直线为同一条直线.
6.直线l同侧有A、B、C三点,如果A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行,则A、B、C三点的位置关系是 ,其理论依据是 .
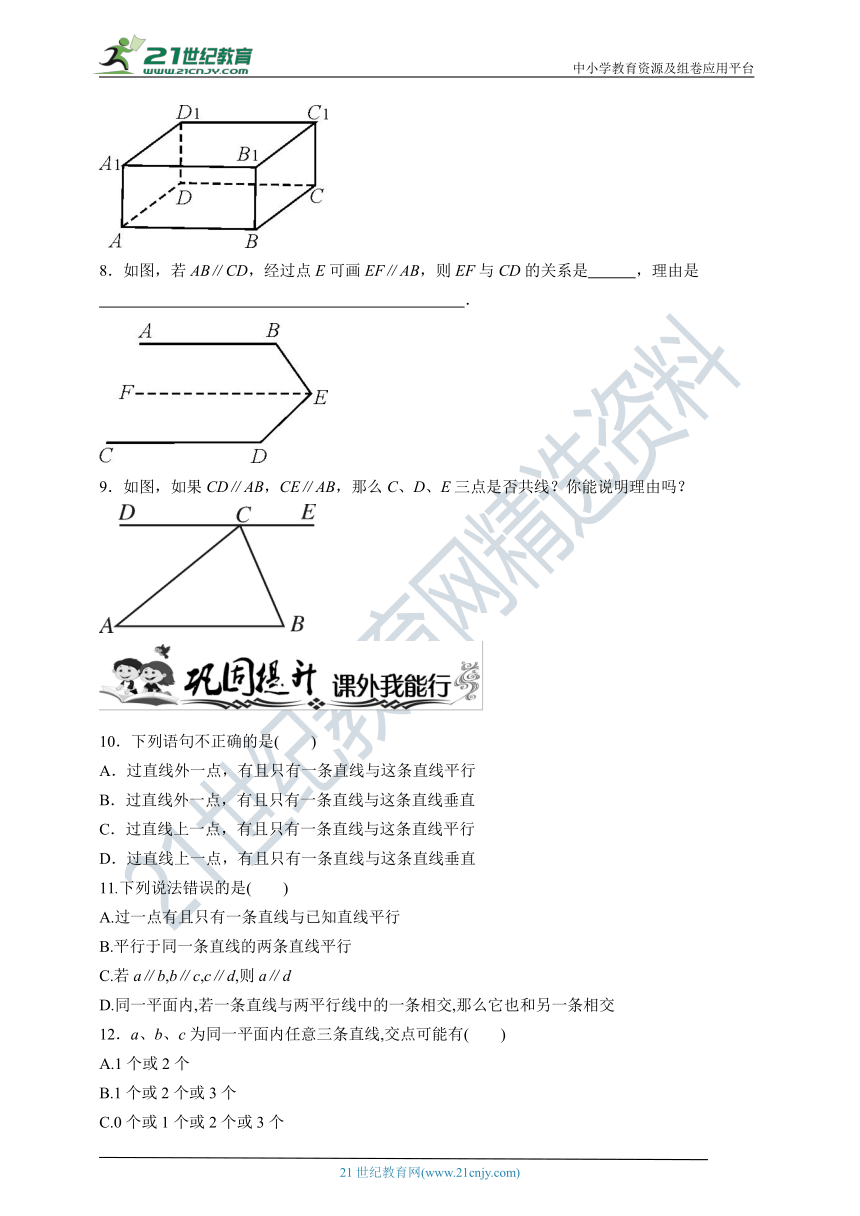
7.观察如图所示的长方体后,用符号表示下列两棱的位置关系:
A1B1 AB,AA1 AB,A1D1 C1D1,AD BC.
8.如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的关系是 ,理由是
.
9.如图,如果CD∥AB,CE∥AB,那么C、D、E三点是否共线?你能说明理由吗?
10.下列语句不正确的是( )
A.过直线外一点,有且只有一条直线与这条直线平行
B.过直线外一点,有且只有一条直线与这条直线垂直
C.过直线上一点,有且只有一条直线与这条直线平行
D.过直线上一点,有且只有一条直线与这条直线垂直
11.下列说法错误的是( )
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交
12.a、b、c为同一平面内任意三条直线,交点可能有( )
A.1个或2个
B.1个或2个或3个
C.0个或1个或2个或3个
D.都不对
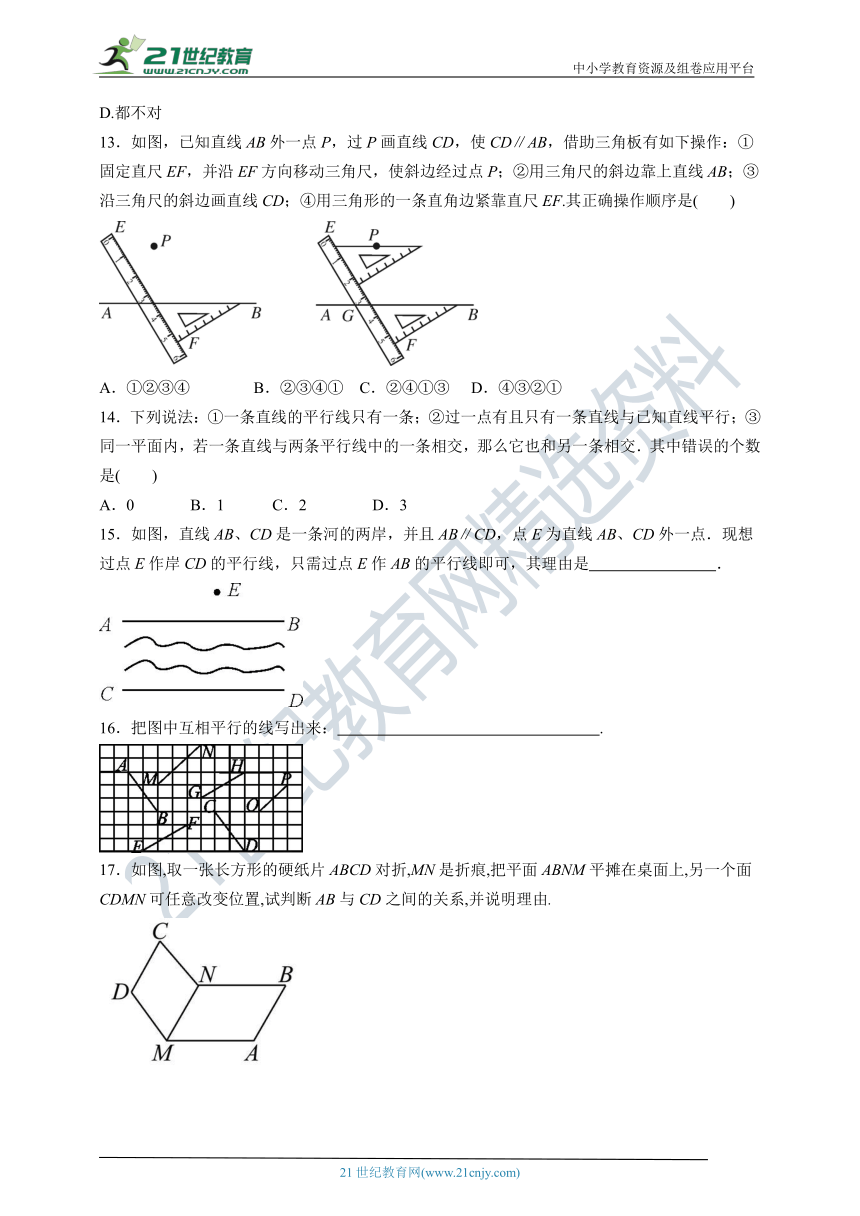
13.如图,已知直线AB外一点P,过P画直线CD,使CD∥AB,借助三角板有如下操作:①固定直尺EF,并沿EF方向移动三角尺,使斜边经过点P;②用三角尺的斜边靠上直线AB;③沿三角尺的斜边画直线CD;④用三角形的一条直角边紧靠直尺EF.其正确操作顺序是( )
A.①②③④ B.②③④① C.②④①③ D.④③②①
14.下列说法:①一条直线的平行线只有一条;②过一点有且只有一条直线与已知直线平行;③同一平面内,若一条直线与两条平行线中的一条相交,那么它也和另一条相交.其中错误的个数是( )
A.0 B.1 C.2 D.3
15.如图,直线AB、CD是一条河的两岸,并且AB∥CD,点E为直线AB、CD外一点.现想过点E作岸CD的平行线,只需过点E作AB的平行线即可,其理由是 .
16.把图中互相平行的线写出来: .
17.如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把平面ABNM平摊在桌面上,另一个面CDMN可任意改变位置,试判断AB与CD之间的关系,并说明理由.
18.如图,P、Q分别是直线EF外两点.
(1)过P画直线AB∥EF,过Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系 为什么
19.【2022·长沙雅礼中学模拟】如图,P是线段AB的中点,过点P画BC的平行线交AC于点Q,再过点Q画AB的平行线交BC于点S.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系.
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你发现了什么?用简洁的语言把你发现的规律叙述出来.
20.【逻辑推理】问题:两条直线可以将平面分成几部分?
解:如图a,两条直线平行时,它们将平面分成三部分;如图b,两条直线不平行时,它们将平面分成四部分.根据上述内容,解答下面的问题.
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类”或 “整体处理”).
(2)三条直线可以将平面分成几部分?
21.[实践]
①画∠AOB=60°,在∠AOB内任取一点P,过点P作直线CD∥AO,又过点P作直线EF∥OB;
②测量:∠CPE、∠EPD、∠DPF、∠CPF的度数.
[探究]
①这些角的边与∠AOB的边有何关系
②这些角的度数与∠AOB的度数之间存在什么关系
[发现]把你的发现用一句话概括出来.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列说法正确的是( C )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
2.下列表示方法正确的是( D )
A.a∥A B.AB∥cd C.A∥B D.a∥b
3.如果线段AB与线段CD没有交点,则( C )
A.线段AB与线段CD一定平行
B.线段AB与线段CD一定不平行
C.线段AB与线段CD可能平行
D.以上说法都不正确
4.如图,能相交的是 ,平行的是 .
【答案】③ ⑤
5.(1)同一平面内 的两条直线,叫做平行线.平行线用“ ”符号表示,读作 .
【答案】不相交 ∥ 平行
(2)过直线外一点 一条直线与这条直线平行.平行于同一条直线的两条直线 .
【答案】有且只有 相互平行
(3)说明三点共线的方法,一是计算夹角为 ;二是说明过两点确定的两条直线为同一条直线.
【答案】180°
6.直线l同侧有A、B、C三点,如果A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行,则A、B、C三点的位置关系是 ,其理论依据是 .
【答案】在同一条直线 过直线外一点,有且只有一条直线与已知直线平行
7.观察如图所示的长方体后,用符号表示下列两棱的位置关系:
A1B1 AB,AA1 AB,A1D1 C1D1,AD BC.
【答案】∥ ⊥ ⊥ ∥
8.如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的关系是 ,理由是
.
【答案】平行
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
9.如图,如果CD∥AB,CE∥AB,那么C、D、E三点是否共线?你能说明理由吗?
解:C、D、E三点共线.理由如下:因为CD∥AB,CE∥AB,所以根据平行公理,知CD与CE是同一条直线,所以C、D、E三点共线.
10.下列语句不正确的是( C )
A.过直线外一点,有且只有一条直线与这条直线平行
B.过直线外一点,有且只有一条直线与这条直线垂直
C.过直线上一点,有且只有一条直线与这条直线平行
D.过直线上一点,有且只有一条直线与这条直线垂直
11.下列说法错误的是( A )
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交
12.a、b、c为同一平面内任意三条直线,交点可能有( C )
A.1个或2个
B.1个或2个或3个
C.0个或1个或2个或3个
D.都不对
13.如图,已知直线AB外一点P,过P画直线CD,使CD∥AB,借助三角板有如下操作:①固定直尺EF,并沿EF方向移动三角尺,使斜边经过点P;②用三角尺的斜边靠上直线AB;③沿三角尺的斜边画直线CD;④用三角形的一条直角边紧靠直尺EF.其正确操作顺序是( C )
A.①②③④ B.②③④① C.②④①③ D.④③②①
14.下列说法:①一条直线的平行线只有一条;②过一点有且只有一条直线与已知直线平行;③同一平面内,若一条直线与两条平行线中的一条相交,那么它也和另一条相交.其中错误的个数是( C )
A.0 B.1 C.2 D.3
15.如图,直线AB、CD是一条河的两岸,并且AB∥CD,点E为直线AB、CD外一点.现想过点E作岸CD的平行线,只需过点E作AB的平行线即可,其理由是 .
【答案】如果两条直线都与第三条直线平行,那么这两条直线也互相平行
16.把图中互相平行的线写出来: .
【答案】MN∥OP,AB∥CD,EF∥GH
17.如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把平面ABNM平摊在桌面上,另一个面CDMN可任意改变位置,试判断AB与CD之间的关系,并说明理由.
解:AB与CD平行.理由:∵AB∥MN,CD∥MN,∴AB∥CD.
18.如图,P、Q分别是直线EF外两点.
(1)过P画直线AB∥EF,过Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系 为什么
解:(1)如图;
(2)AB∥CD.理由:因为AB∥EF,CD∥EF,所以AB∥CD.
19.【2022·长沙雅礼中学模拟】如图,P是线段AB的中点,过点P画BC的平行线交AC于点Q,再过点Q画AB的平行线交BC于点S.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系.
解:所画图形如图所示.
(1)经测量得到AQ=QC,CS=BS.
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你发现了什么?用简洁的语言把你发现的规律叙述出来.
经测量得到PQ=BC,QS=AB.经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边;三角形两边中点之间线段的长度等于第三边长度的一半.
20.【逻辑推理】问题:两条直线可以将平面分成几部分?
解:如图a,两条直线平行时,它们将平面分成三部分;如图b,两条直线不平行时,它们将平面分成四部分.根据上述内容,解答下面的问题.
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类”或 “整体处理”).
【答案】分类
(2)三条直线可以将平面分成几部分?
如图所示.三条直线可以把平面分成四部分或六部分或七部分.
【思路点拨】根据三条直线的交点个数情况(0个、1个、2个、3个)进行分类讨论.
21.[实践]
①画∠AOB=60°,在∠AOB内任取一点P,过点P作直线CD∥AO,又过点P作直线EF∥OB;
②测量:∠CPE、∠EPD、∠DPF、∠CPF的度数.
[探究]
①这些角的边与∠AOB的边有何关系
②这些角的度数与∠AOB的度数之间存在什么关系
[发现]把你的发现用一句话概括出来.
解:[实践]:①画图;
②∠CPE=120°,∠EPD=60°,∠DPF=120°,∠CPF=60°;
[探究]:①平行,②相等或互补;
[发现]:如果两个角的两边分别平行,那么这两个角相等或互补
5.2.1 平行线
1.下列说法正确的是( )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
2.下列表示方法正确的是( )
A.a∥A B.AB∥cd C.A∥B D.a∥b
3.如果线段AB与线段CD没有交点,则( )
A.线段AB与线段CD一定平行
B.线段AB与线段CD一定不平行
C.线段AB与线段CD可能平行
D.以上说法都不正确
4.如图,能相交的是 ,平行的是 .
5.(1)同一平面内 的两条直线,叫做平行线.平行线用“ ”符号表示,读作 .
(2)过直线外一点 一条直线与这条直线平行.平行于同一条直线的两条直线 .
(3)说明三点共线的方法,一是计算夹角为 ;二是说明过两点确定的两条直线为同一条直线.
6.直线l同侧有A、B、C三点,如果A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行,则A、B、C三点的位置关系是 ,其理论依据是 .
7.观察如图所示的长方体后,用符号表示下列两棱的位置关系:
A1B1 AB,AA1 AB,A1D1 C1D1,AD BC.
8.如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的关系是 ,理由是
.
9.如图,如果CD∥AB,CE∥AB,那么C、D、E三点是否共线?你能说明理由吗?
10.下列语句不正确的是( )
A.过直线外一点,有且只有一条直线与这条直线平行
B.过直线外一点,有且只有一条直线与这条直线垂直
C.过直线上一点,有且只有一条直线与这条直线平行
D.过直线上一点,有且只有一条直线与这条直线垂直
11.下列说法错误的是( )
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交
12.a、b、c为同一平面内任意三条直线,交点可能有( )
A.1个或2个
B.1个或2个或3个
C.0个或1个或2个或3个
D.都不对
13.如图,已知直线AB外一点P,过P画直线CD,使CD∥AB,借助三角板有如下操作:①固定直尺EF,并沿EF方向移动三角尺,使斜边经过点P;②用三角尺的斜边靠上直线AB;③沿三角尺的斜边画直线CD;④用三角形的一条直角边紧靠直尺EF.其正确操作顺序是( )
A.①②③④ B.②③④① C.②④①③ D.④③②①
14.下列说法:①一条直线的平行线只有一条;②过一点有且只有一条直线与已知直线平行;③同一平面内,若一条直线与两条平行线中的一条相交,那么它也和另一条相交.其中错误的个数是( )
A.0 B.1 C.2 D.3
15.如图,直线AB、CD是一条河的两岸,并且AB∥CD,点E为直线AB、CD外一点.现想过点E作岸CD的平行线,只需过点E作AB的平行线即可,其理由是 .
16.把图中互相平行的线写出来: .
17.如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把平面ABNM平摊在桌面上,另一个面CDMN可任意改变位置,试判断AB与CD之间的关系,并说明理由.
18.如图,P、Q分别是直线EF外两点.
(1)过P画直线AB∥EF,过Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系 为什么
19.【2022·长沙雅礼中学模拟】如图,P是线段AB的中点,过点P画BC的平行线交AC于点Q,再过点Q画AB的平行线交BC于点S.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系.
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你发现了什么?用简洁的语言把你发现的规律叙述出来.
20.【逻辑推理】问题:两条直线可以将平面分成几部分?
解:如图a,两条直线平行时,它们将平面分成三部分;如图b,两条直线不平行时,它们将平面分成四部分.根据上述内容,解答下面的问题.
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类”或 “整体处理”).
(2)三条直线可以将平面分成几部分?
21.[实践]
①画∠AOB=60°,在∠AOB内任取一点P,过点P作直线CD∥AO,又过点P作直线EF∥OB;
②测量:∠CPE、∠EPD、∠DPF、∠CPF的度数.
[探究]
①这些角的边与∠AOB的边有何关系
②这些角的度数与∠AOB的度数之间存在什么关系
[发现]把你的发现用一句话概括出来.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列说法正确的是( C )
A.同一平面内没有公共点的两条线段平行
B.两条不相交的直线是平行线
C.同一平面内没有公共点的两条直线平行
D.同一平面内没有公共点的两条射线平行
2.下列表示方法正确的是( D )
A.a∥A B.AB∥cd C.A∥B D.a∥b
3.如果线段AB与线段CD没有交点,则( C )
A.线段AB与线段CD一定平行
B.线段AB与线段CD一定不平行
C.线段AB与线段CD可能平行
D.以上说法都不正确
4.如图,能相交的是 ,平行的是 .
【答案】③ ⑤
5.(1)同一平面内 的两条直线,叫做平行线.平行线用“ ”符号表示,读作 .
【答案】不相交 ∥ 平行
(2)过直线外一点 一条直线与这条直线平行.平行于同一条直线的两条直线 .
【答案】有且只有 相互平行
(3)说明三点共线的方法,一是计算夹角为 ;二是说明过两点确定的两条直线为同一条直线.
【答案】180°
6.直线l同侧有A、B、C三点,如果A、B两点确定的直线l1与B、C两点确定的直线l2都与l平行,则A、B、C三点的位置关系是 ,其理论依据是 .
【答案】在同一条直线 过直线外一点,有且只有一条直线与已知直线平行
7.观察如图所示的长方体后,用符号表示下列两棱的位置关系:
A1B1 AB,AA1 AB,A1D1 C1D1,AD BC.
【答案】∥ ⊥ ⊥ ∥
8.如图,若AB∥CD,经过点E可画EF∥AB,则EF与CD的关系是 ,理由是
.
【答案】平行
如果两条直线都与第三条直线平行,那么这两条直线也互相平行
9.如图,如果CD∥AB,CE∥AB,那么C、D、E三点是否共线?你能说明理由吗?
解:C、D、E三点共线.理由如下:因为CD∥AB,CE∥AB,所以根据平行公理,知CD与CE是同一条直线,所以C、D、E三点共线.
10.下列语句不正确的是( C )
A.过直线外一点,有且只有一条直线与这条直线平行
B.过直线外一点,有且只有一条直线与这条直线垂直
C.过直线上一点,有且只有一条直线与这条直线平行
D.过直线上一点,有且只有一条直线与这条直线垂直
11.下列说法错误的是( A )
A.过一点有且只有一条直线与已知直线平行
B.平行于同一条直线的两条直线平行
C.若a∥b,b∥c,c∥d,则a∥d
D.同一平面内,若一条直线与两平行线中的一条相交,那么它也和另一条相交
12.a、b、c为同一平面内任意三条直线,交点可能有( C )
A.1个或2个
B.1个或2个或3个
C.0个或1个或2个或3个
D.都不对
13.如图,已知直线AB外一点P,过P画直线CD,使CD∥AB,借助三角板有如下操作:①固定直尺EF,并沿EF方向移动三角尺,使斜边经过点P;②用三角尺的斜边靠上直线AB;③沿三角尺的斜边画直线CD;④用三角形的一条直角边紧靠直尺EF.其正确操作顺序是( C )
A.①②③④ B.②③④① C.②④①③ D.④③②①
14.下列说法:①一条直线的平行线只有一条;②过一点有且只有一条直线与已知直线平行;③同一平面内,若一条直线与两条平行线中的一条相交,那么它也和另一条相交.其中错误的个数是( C )
A.0 B.1 C.2 D.3
15.如图,直线AB、CD是一条河的两岸,并且AB∥CD,点E为直线AB、CD外一点.现想过点E作岸CD的平行线,只需过点E作AB的平行线即可,其理由是 .
【答案】如果两条直线都与第三条直线平行,那么这两条直线也互相平行
16.把图中互相平行的线写出来: .
【答案】MN∥OP,AB∥CD,EF∥GH
17.如图,取一张长方形的硬纸片ABCD对折,MN是折痕,把平面ABNM平摊在桌面上,另一个面CDMN可任意改变位置,试判断AB与CD之间的关系,并说明理由.
解:AB与CD平行.理由:∵AB∥MN,CD∥MN,∴AB∥CD.
18.如图,P、Q分别是直线EF外两点.
(1)过P画直线AB∥EF,过Q画直线CD∥EF;
(2)AB与CD有怎样的位置关系 为什么
解:(1)如图;
(2)AB∥CD.理由:因为AB∥EF,CD∥EF,所以AB∥CD.
19.【2022·长沙雅礼中学模拟】如图,P是线段AB的中点,过点P画BC的平行线交AC于点Q,再过点Q画AB的平行线交BC于点S.
(1)用刻度尺测量后确定AQ与QC,CS与BS的数量关系.
解:所画图形如图所示.
(1)经测量得到AQ=QC,CS=BS.
(2)用刻度尺测量后确定PQ与BC,QS与AB的数量关系,你发现了什么?用简洁的语言把你发现的规律叙述出来.
经测量得到PQ=BC,QS=AB.经过三角形一边的中点,画另一边的平行线,则这条平行线平分第三边;三角形两边中点之间线段的长度等于第三边长度的一半.
20.【逻辑推理】问题:两条直线可以将平面分成几部分?
解:如图a,两条直线平行时,它们将平面分成三部分;如图b,两条直线不平行时,它们将平面分成四部分.根据上述内容,解答下面的问题.
(1)上面问题的解题过程应用了________的数学思想(填“转化”“分类”或 “整体处理”).
【答案】分类
(2)三条直线可以将平面分成几部分?
如图所示.三条直线可以把平面分成四部分或六部分或七部分.
【思路点拨】根据三条直线的交点个数情况(0个、1个、2个、3个)进行分类讨论.
21.[实践]
①画∠AOB=60°,在∠AOB内任取一点P,过点P作直线CD∥AO,又过点P作直线EF∥OB;
②测量:∠CPE、∠EPD、∠DPF、∠CPF的度数.
[探究]
①这些角的边与∠AOB的边有何关系
②这些角的度数与∠AOB的度数之间存在什么关系
[发现]把你的发现用一句话概括出来.
解:[实践]:①画图;
②∠CPE=120°,∠EPD=60°,∠DPF=120°,∠CPF=60°;
[探究]:①平行,②相等或互补;
[发现]:如果两个角的两边分别平行,那么这两个角相等或互补
