5.3.1.1 平行线的性质 同步练习(含答案)
文档属性
| 名称 | 5.3.1.1 平行线的性质 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 11:16:57 | ||
图片预览


文档简介
5.3 平行线的性质
5.3.1 平行线的性质
第1课时 平行线的性质
1.如图直线a∥b,∠1=60°,则∠2等于( )
A.30° B.60° C.45° D.120°
2.如图,DE∥AB,若∠ACD=55°,则∠A等于( )
A.35° B.55° C.65° D.125°
3.如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( )
A.65° B.55° C.45° D.35°
4.如图,一条“U”形水管中AB∥CD,若∠B=75°,则∠C等于( )
A.75° B.95° C.105° D.125°
5.(1)两直线平行,同位角 .
(2)两直线平行,内错角 .
(3)两直线平行,同旁内角 .
6.如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为 .
7.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
8.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
9.【2022·广东】如图,直线a∥b,∠1=40°,则∠2=( )
A.30° B.40° C.50° D.60°
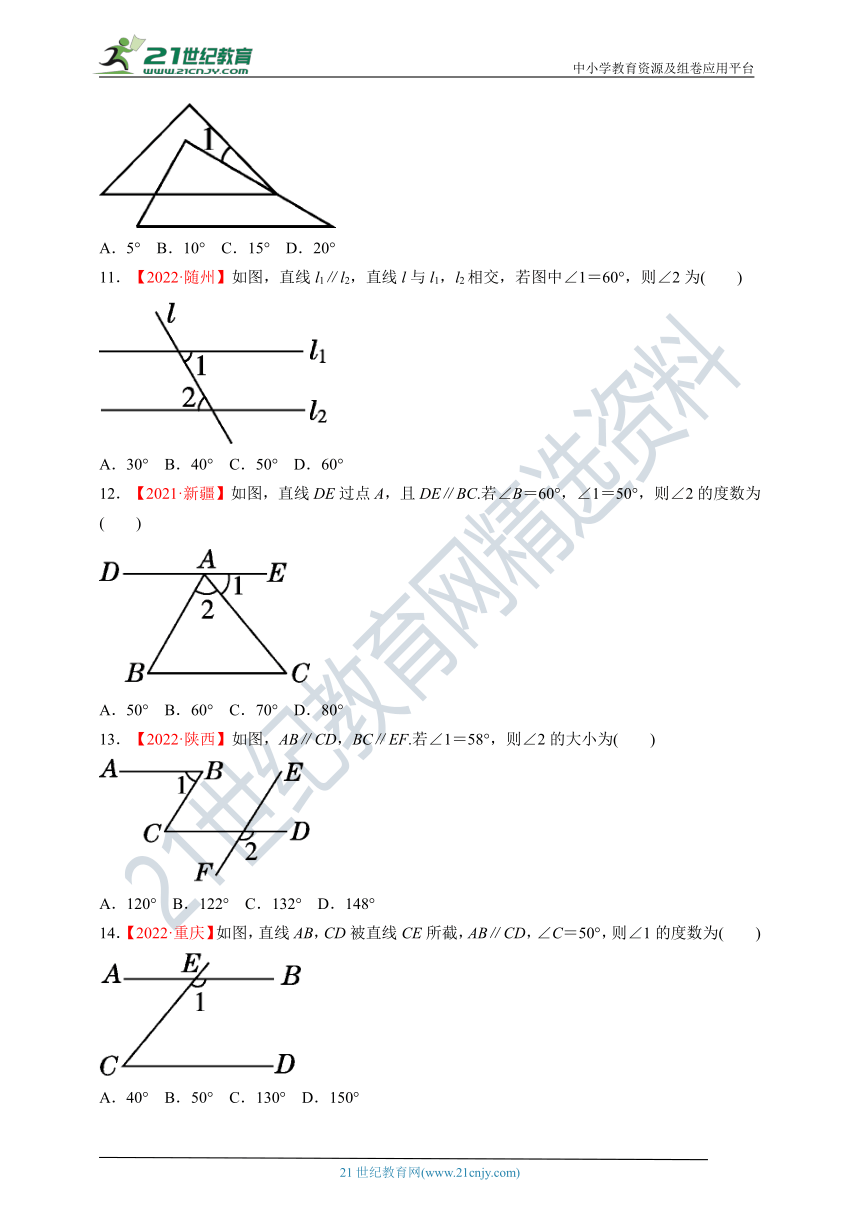
10.【2022·深圳】一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5° B.10° C.15° D.20°
11.【2022·随州】如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
12.【2021·新疆】如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
13.【2022·陕西】如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为( )
A.120° B.122° C.132° D.148°
14.【2022·重庆】如图,直线AB,CD被直线CE所截,AB∥CD,∠C=50°,则∠1的度数为( )
A.40° B.50° C.130° D.150°
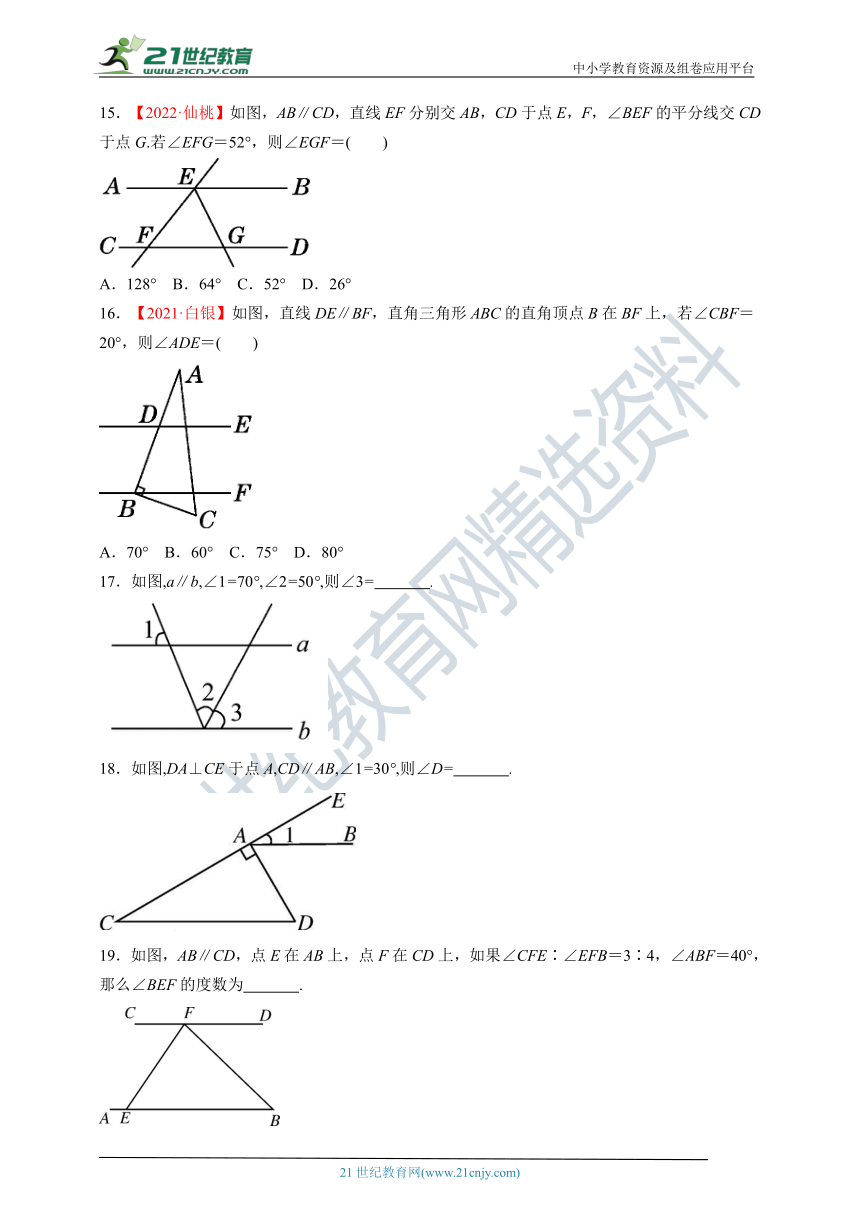
15.【2022·仙桃】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( )
A.128° B.64° C.52° D.26°
16.【2021·白银】如图,直线DE∥BF,直角三角形ABC的直角顶点B在BF上,若∠CBF=20°,则∠ADE=( )
A.70° B.60° C.75° D.80°
17.如图,a∥b,∠1=70°,∠2=50°,则∠3= .
18.如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
19.如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
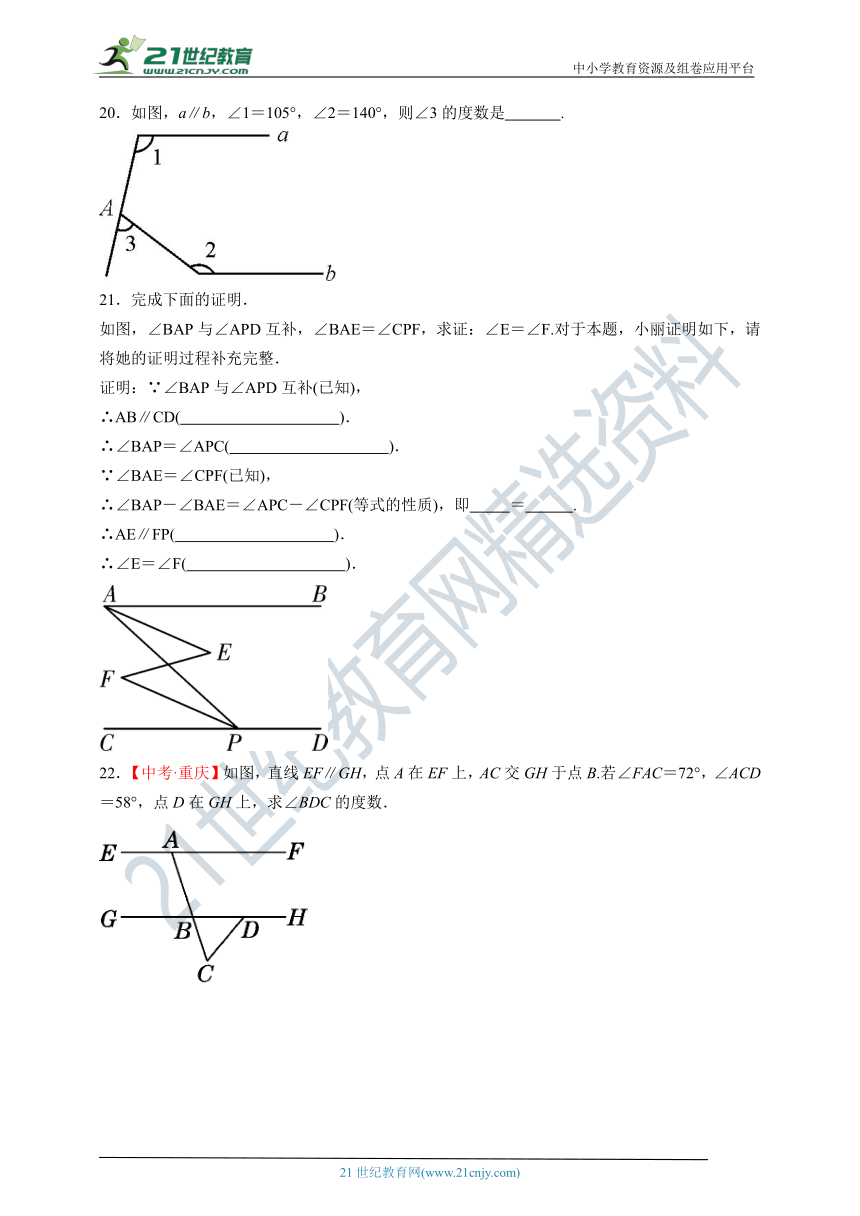
20.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是 .
21.完成下面的证明.
如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题,小丽证明如下,请将她的证明过程补充完整.
证明:∵∠BAP与∠APD互补(已知),
∴AB∥CD( ).
∴∠BAP=∠APC( ).
∵∠BAE=∠CPF(已知),
∴∠BAP-∠BAE=∠APC-∠CPF(等式的性质),即 = .
∴AE∥FP( ).
∴∠E=∠F( ).
22.【中考·重庆】如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
23.如图,BD⊥AC于点D,EF⊥AC于点F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
24.【2022·呼和浩特秋实中学模拟】把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′,C′的位置上,ED′与BC的交点为G,如图所示.若∠EFG=60°,求∠1与∠2的度数.
25.【2021·武汉】如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.试说明:∠DEF=∠F.
26.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
27.如图,已知直线l1∥l2,且l3与l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图直线a∥b,∠1=60°,则∠2等于( B )
A.30° B.60° C.45° D.120°
2.如图,DE∥AB,若∠ACD=55°,则∠A等于( B )
A.35° B.55° C.65° D.125°
3.如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( B )
A.65° B.55° C.45° D.35°
4.如图,一条“U”形水管中AB∥CD,若∠B=75°,则∠C等于( C )
A.75° B.95° C.105° D.125°
5.(1)两直线平行,同位角 .
【答案】相等
(2)两直线平行,内错角 .
【答案】相等
(3)两直线平行,同旁内角 .
【答案】互补
6.如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为 .
【答案】50°
7.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
【答案】60°
8.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°-∠ABD=50°,∴∠2=∠BDC=50°.
9.【2022·广东】如图,直线a∥b,∠1=40°,则∠2=( B )
A.30° B.40° C.50° D.60°
10.【2022·深圳】一副三角板如图所示放置,斜边平行,则∠1的度数为( C )
A.5° B.10° C.15° D.20°
11.【2022·随州】如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( D )
A.30° B.40° C.50° D.60°
12.【2021·新疆】如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( C )
A.50° B.60° C.70° D.80°
13.【2022·陕西】如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为( B )
A.120° B.122° C.132° D.148°
14.【2022·重庆】如图,直线AB,CD被直线CE所截,AB∥CD,∠C=50°,则∠1的度数为( C )
A.40° B.50° C.130° D.150°
15.【2022·仙桃】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( B )
A.128° B.64° C.52° D.26°
16.【2021·白银】如图,直线DE∥BF,直角三角形ABC的直角顶点B在BF上,若∠CBF=20°,则∠ADE=( A )
A.70° B.60° C.75° D.80°
【点拨】∵∠ABC=90°,∠CBF=20°,
∴∠ABF=∠ABC-∠CBF=70°.
∵DE∥BF,
∴∠ADE=∠ABF=70°.
17.如图,a∥b,∠1=70°,∠2=50°,则∠3= 60° .
18.如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= 60° .
19.如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
【答案】60°
20.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是 .
【答案】65°
21.完成下面的证明.
如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题,小丽证明如下,请将她的证明过程补充完整.
证明:∵∠BAP与∠APD互补(已知),
∴AB∥CD(同旁内角互补,两直 线平行).
∴∠BAP=∠APC(两直线平行, 内错角相等).
∵∠BAE=∠CPF(已知),
∴∠BAP-∠BAE=∠APC-∠CPF(等式的性质),即∠EAP=∠APF.
∴AE∥FP(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
22.【中考·重庆】如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
解:∵EF∥GH,∴∠DBC=∠FAC=72°.
∵三角形的内角和为180°,
∴∠BDC=180°-∠DBC-∠ACD
=180°-72°-58°=50°.
23.如图,BD⊥AC于点D,EF⊥AC于点F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
(1)解:∵BD⊥AC,EF⊥AC,BD∥EF,∴∠EFG=∠1=35°,∴∠GFC=90°+35°=125°;
(2)证明:由(1)知,∠EFG=∠1,而∠1=∠2,∴∠EFG=∠2,∴GF∥BC.∴∠AMD=∠AGF,∴MD∥GF,∴DM∥BC.
24.【2022·呼和浩特秋实中学模拟】把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′,C′的位置上,ED′与BC的交点为G,如图所示.若∠EFG=60°,求∠1与∠2的度数.
解:∵四边形ABCD是长方形,∴AD∥BC.
∴∠DEF=∠EFG=60°,∠1+∠2=180°.
由折叠易得∠DEF=∠D′EF,
∴∠DEF=∠D′EF=60°.
∴∠1=180°-∠DEF-∠D′EF=60°.
∵∠1+∠2=180°,
∴∠2=120°.
25.【2021·武汉】如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.试说明:∠DEF=∠F.
解:∵AB∥CD,∴∠DCF=∠B.
∵∠B=∠D,∴∠DCF=∠D.
∴AD∥BC.
∴∠DEF=∠F.
【点要点】平行线和角的数量关系是紧密联系在一起的,由平行线可以得到角的数量关系,反过来又可以由角的数量关系得到新的一组平行线,这种角的数量关系与直线的位置关系的相互转化在解题中会经常涉及.
26.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
解:∠AED=∠C.理由:∵∠1+∠2=180°,
∠1+∠4=180°,∴∠2=∠4,
∴EF∥AB,∴∠3=∠ADE.
又∵∠3=∠B,∴∠ADE=∠B,
∴DE∥BC,∴∠AED=∠C.
27.如图,已知直线l1∥l2,且l3与l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合).
解:(1)∠1+∠2=∠3.理由:如图,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠1=∠4,∠2=∠5.∵∠4+∠5=∠3,∴∠1+∠2=∠3;
(2)∠1+∠2=∠3不变;
(3)∠1-∠2=∠3或∠2-∠1=∠3.理由:
①当点P在下侧时,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠2=∠4,∠1=∠3+∠4,∴∠1-∠2=∠3.②当点P在上侧时,同理可得∠2-∠1=∠3.
5.3.1 平行线的性质
第1课时 平行线的性质
1.如图直线a∥b,∠1=60°,则∠2等于( )
A.30° B.60° C.45° D.120°
2.如图,DE∥AB,若∠ACD=55°,则∠A等于( )
A.35° B.55° C.65° D.125°
3.如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( )
A.65° B.55° C.45° D.35°
4.如图,一条“U”形水管中AB∥CD,若∠B=75°,则∠C等于( )
A.75° B.95° C.105° D.125°
5.(1)两直线平行,同位角 .
(2)两直线平行,内错角 .
(3)两直线平行,同旁内角 .
6.如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为 .
7.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
8.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
9.【2022·广东】如图,直线a∥b,∠1=40°,则∠2=( )
A.30° B.40° C.50° D.60°
10.【2022·深圳】一副三角板如图所示放置,斜边平行,则∠1的度数为( )
A.5° B.10° C.15° D.20°
11.【2022·随州】如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( )
A.30° B.40° C.50° D.60°
12.【2021·新疆】如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( )
A.50° B.60° C.70° D.80°
13.【2022·陕西】如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为( )
A.120° B.122° C.132° D.148°
14.【2022·重庆】如图,直线AB,CD被直线CE所截,AB∥CD,∠C=50°,则∠1的度数为( )
A.40° B.50° C.130° D.150°
15.【2022·仙桃】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( )
A.128° B.64° C.52° D.26°
16.【2021·白银】如图,直线DE∥BF,直角三角形ABC的直角顶点B在BF上,若∠CBF=20°,则∠ADE=( )
A.70° B.60° C.75° D.80°
17.如图,a∥b,∠1=70°,∠2=50°,则∠3= .
18.如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
19.如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
20.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是 .
21.完成下面的证明.
如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题,小丽证明如下,请将她的证明过程补充完整.
证明:∵∠BAP与∠APD互补(已知),
∴AB∥CD( ).
∴∠BAP=∠APC( ).
∵∠BAE=∠CPF(已知),
∴∠BAP-∠BAE=∠APC-∠CPF(等式的性质),即 = .
∴AE∥FP( ).
∴∠E=∠F( ).
22.【中考·重庆】如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
23.如图,BD⊥AC于点D,EF⊥AC于点F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
24.【2022·呼和浩特秋实中学模拟】把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′,C′的位置上,ED′与BC的交点为G,如图所示.若∠EFG=60°,求∠1与∠2的度数.
25.【2021·武汉】如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.试说明:∠DEF=∠F.
26.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
27.如图,已知直线l1∥l2,且l3与l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合).
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图直线a∥b,∠1=60°,则∠2等于( B )
A.30° B.60° C.45° D.120°
2.如图,DE∥AB,若∠ACD=55°,则∠A等于( B )
A.35° B.55° C.65° D.125°
3.如图,直线l1∥l2,直角三角板的直角顶点C在直线l1上,一锐角顶点B在直线l2上,若∠1=35°,则∠2的度数是( B )
A.65° B.55° C.45° D.35°
4.如图,一条“U”形水管中AB∥CD,若∠B=75°,则∠C等于( C )
A.75° B.95° C.105° D.125°
5.(1)两直线平行,同位角 .
【答案】相等
(2)两直线平行,内错角 .
【答案】相等
(3)两直线平行,同旁内角 .
【答案】互补
6.如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为 .
【答案】50°
7.如图,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF= .
【答案】60°
8.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
解:∵AB∥CD,∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,∵BC平分∠ABD,∴∠ABD=2∠ABC=130°,∴∠BDC=180°-∠ABD=50°,∴∠2=∠BDC=50°.
9.【2022·广东】如图,直线a∥b,∠1=40°,则∠2=( B )
A.30° B.40° C.50° D.60°
10.【2022·深圳】一副三角板如图所示放置,斜边平行,则∠1的度数为( C )
A.5° B.10° C.15° D.20°
11.【2022·随州】如图,直线l1∥l2,直线l与l1,l2相交,若图中∠1=60°,则∠2为( D )
A.30° B.40° C.50° D.60°
12.【2021·新疆】如图,直线DE过点A,且DE∥BC.若∠B=60°,∠1=50°,则∠2的度数为( C )
A.50° B.60° C.70° D.80°
13.【2022·陕西】如图,AB∥CD,BC∥EF.若∠1=58°,则∠2的大小为( B )
A.120° B.122° C.132° D.148°
14.【2022·重庆】如图,直线AB,CD被直线CE所截,AB∥CD,∠C=50°,则∠1的度数为( C )
A.40° B.50° C.130° D.150°
15.【2022·仙桃】如图,AB∥CD,直线EF分别交AB,CD于点E,F,∠BEF的平分线交CD于点G.若∠EFG=52°,则∠EGF=( B )
A.128° B.64° C.52° D.26°
16.【2021·白银】如图,直线DE∥BF,直角三角形ABC的直角顶点B在BF上,若∠CBF=20°,则∠ADE=( A )
A.70° B.60° C.75° D.80°
【点拨】∵∠ABC=90°,∠CBF=20°,
∴∠ABF=∠ABC-∠CBF=70°.
∵DE∥BF,
∴∠ADE=∠ABF=70°.
17.如图,a∥b,∠1=70°,∠2=50°,则∠3= 60° .
18.如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= 60° .
19.如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE∶∠EFB=3∶4,∠ABF=40°,那么∠BEF的度数为 .
【答案】60°
20.如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是 .
【答案】65°
21.完成下面的证明.
如图,∠BAP与∠APD互补,∠BAE=∠CPF,求证:∠E=∠F.对于本题,小丽证明如下,请将她的证明过程补充完整.
证明:∵∠BAP与∠APD互补(已知),
∴AB∥CD(同旁内角互补,两直 线平行).
∴∠BAP=∠APC(两直线平行, 内错角相等).
∵∠BAE=∠CPF(已知),
∴∠BAP-∠BAE=∠APC-∠CPF(等式的性质),即∠EAP=∠APF.
∴AE∥FP(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
22.【中考·重庆】如图,直线EF∥GH,点A在EF上,AC交GH于点B.若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
解:∵EF∥GH,∴∠DBC=∠FAC=72°.
∵三角形的内角和为180°,
∴∠BDC=180°-∠DBC-∠ACD
=180°-72°-58°=50°.
23.如图,BD⊥AC于点D,EF⊥AC于点F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
(1)解:∵BD⊥AC,EF⊥AC,BD∥EF,∴∠EFG=∠1=35°,∴∠GFC=90°+35°=125°;
(2)证明:由(1)知,∠EFG=∠1,而∠1=∠2,∴∠EFG=∠2,∴GF∥BC.∴∠AMD=∠AGF,∴MD∥GF,∴DM∥BC.
24.【2022·呼和浩特秋实中学模拟】把一张长方形纸片ABCD沿EF折叠后,D,C分别落在D′,C′的位置上,ED′与BC的交点为G,如图所示.若∠EFG=60°,求∠1与∠2的度数.
解:∵四边形ABCD是长方形,∴AD∥BC.
∴∠DEF=∠EFG=60°,∠1+∠2=180°.
由折叠易得∠DEF=∠D′EF,
∴∠DEF=∠D′EF=60°.
∴∠1=180°-∠DEF-∠D′EF=60°.
∵∠1+∠2=180°,
∴∠2=120°.
25.【2021·武汉】如图,AB∥CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.试说明:∠DEF=∠F.
解:∵AB∥CD,∴∠DCF=∠B.
∵∠B=∠D,∴∠DCF=∠D.
∴AD∥BC.
∴∠DEF=∠F.
【点要点】平行线和角的数量关系是紧密联系在一起的,由平行线可以得到角的数量关系,反过来又可以由角的数量关系得到新的一组平行线,这种角的数量关系与直线的位置关系的相互转化在解题中会经常涉及.
26.如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并说明你的理由.
解:∠AED=∠C.理由:∵∠1+∠2=180°,
∠1+∠4=180°,∴∠2=∠4,
∴EF∥AB,∴∠3=∠ADE.
又∵∠3=∠B,∴∠ADE=∠B,
∴DE∥BC,∴∠AED=∠C.
27.如图,已知直线l1∥l2,且l3与l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说明理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合).
解:(1)∠1+∠2=∠3.理由:如图,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠1=∠4,∠2=∠5.∵∠4+∠5=∠3,∴∠1+∠2=∠3;
(2)∠1+∠2=∠3不变;
(3)∠1-∠2=∠3或∠2-∠1=∠3.理由:
①当点P在下侧时,过点P作l1的平行线PQ.∵l1∥l2,∴l1∥l2∥PQ,∴∠2=∠4,∠1=∠3+∠4,∴∠1-∠2=∠3.②当点P在上侧时,同理可得∠2-∠1=∠3.
