5.3.1.2 平行线的判定和性质的综合应用 同步练习(含答案)
文档属性
| 名称 | 5.3.1.2 平行线的判定和性质的综合应用 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 11:18:52 | ||
图片预览




文档简介
5.3 平行线的性质
5.3.1 平行线的性质
第2课时 平行线的判定和性质的综合应用
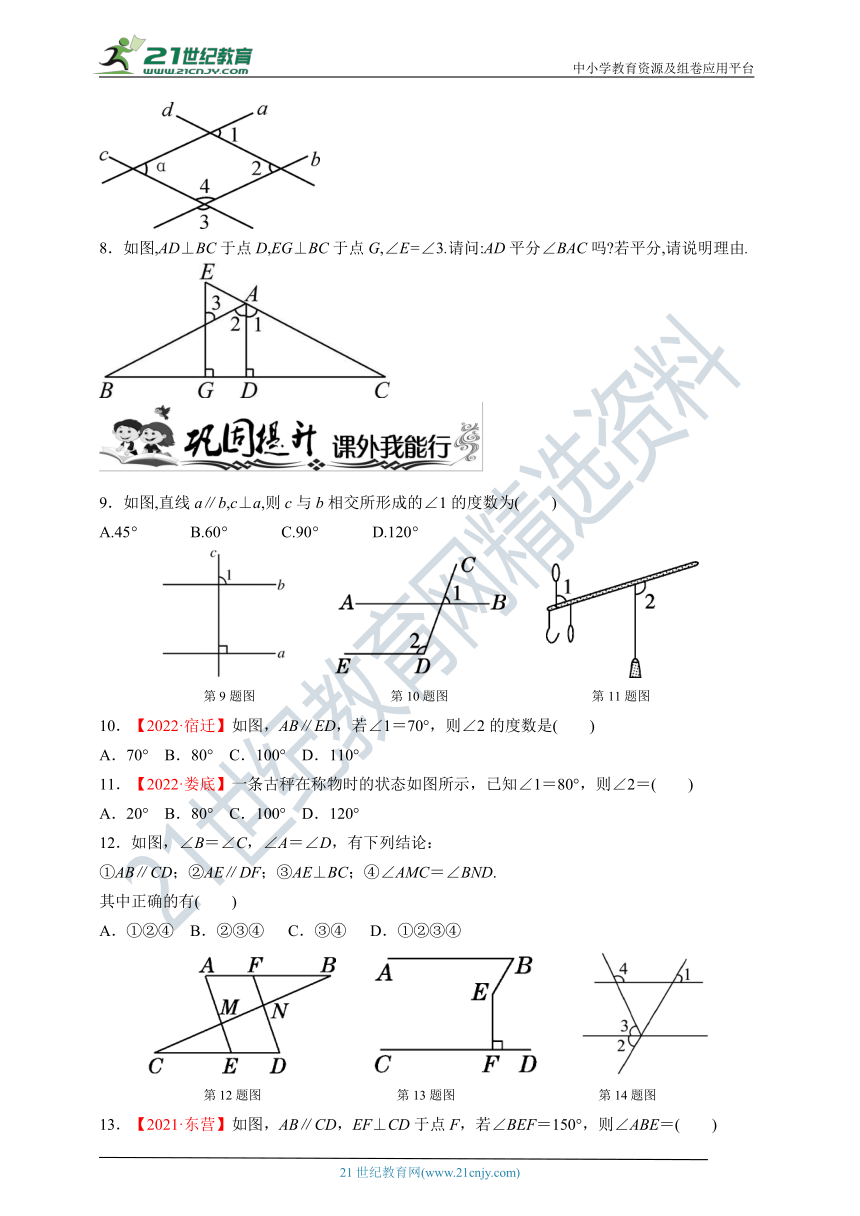
1.如图,直线a、b被直线c、d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数为( )
A.80° B.85° C.95° D.100°
第1题图 第2题图 第3题图
2.如图,a、b、c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为( )
A.70° B.90° C.110° D.80°
3.如图,由A到B的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
4.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
第4题图 第5题图 第6题图
5.如图,已知AB∥CD,则∠BAE+∠AEF+∠EFC+∠FCD的度数为 .
6.一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
7.如图,已知四条直线a、b、c、d,∠1=79°,∠2=79°,∠3=101°.指出图中有哪些直线平行?说明理由,并求出α的度数.
8.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.请问:AD平分∠BAC吗 若平分,请说明理由.
9.如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
A.45° B.60° C.90° D.120°
第9题图 第10题图 第11题图
10.【2022·宿迁】如图,AB∥ED,若∠1=70°,则∠2的度数是( )
A.70° B.80° C.100° D.110°
11.【2022·娄底】一条古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A.20° B.80° C.100° D.120°
12.如图,∠B=∠C,∠A=∠D,有下列结论:
①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有( )
A.①②④ B.②③④ C.③④ D.①②③④
第12题图 第13题图 第14题图
13.【2021·东营】如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( )
A.30° B.40° C.50° D.60°
14.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
15.如图,∠1+∠2=180°,∠3=100°,则∠4等于 .
第15题图 第16题图 第17题图
16.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
17.如图,∠1=∠2,∠A=60°,则∠ADC= 度.
18.【2022·太原五中模拟】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断BC与DE的位置关系,并说明理由;
(2)若∠A=35°,求∠F的度数.
19.【逻辑推理】如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试说明:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠D=30°,求∠AED的度数.
20.【2022·武汉】如图,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
(2)AE平分∠BAD交BC于点E,∠BCD=50°,试说明:AE∥DC.
21.(1)如图1,已知∠B=25°,∠BED=80°,∠D=55°,探究AB与CD有怎样的位置关系;
(2)如图2,已知AB∥EF,试猜想∠B、∠F、∠BCF之间的关系,写出这种关系,并加以证明.
22.【阅读探究题】【探索】小明和小亮在研究一个数学问题:
如图,已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
【发现】小明和小亮都发现∠APC=∠A+∠C.
小明是这样解答的:如图,过点P在∠APC的内部作PQ∥AB,
∴∠APQ=∠A(__________________________).∵PQ∥AB,AB∥CD,∴PQ∥CD(__________________________________).
∴∠CPQ=∠C.∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
小亮是这样解答的:
如图,过点P作PQ∥AB∥CD,
∴∠APQ=∠A,∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面解答过程中的横线上填写依据.
两人的解答过程中,完全正确的是________.
【应用】在图①中,AB∥CD,若∠A=120°,∠C=140°,则∠P的度数为________;在图②中,AB∥CD,若∠A=30°,∠C=70°,则∠P的度数为________.
【拓展】在图③中,AB∥CD,探索∠P与∠A,∠C的数量关系,并说明理由.
23.已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD.求证:∠AFC=∠AEC.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,直线a、b被直线c、d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数为( B )
A.80° B.85° C.95° D.100°
第1题图 第2题图 第3题图
2.如图,a、b、c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为( A )
A.70° B.90° C.110° D.80°
3.如图,由A到B的方向是( B )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
4.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( D )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
第4题图 第5题图 第6题图
5.如图,已知AB∥CD,则∠BAE+∠AEF+∠EFC+∠FCD的度数为
【答案】540°
6.一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
【答案】270°
7.如图,已知四条直线a、b、c、d,∠1=79°,∠2=79°,∠3=101°.指出图中有哪些直线平行?说明理由,并求出α的度数.
解:a∥b,c∥d,∵∠2=∠1=79°,∴a∥b,又∠4=∠3=101°,∴∠2+∠4=180°,∴c∥d,∴∠α=∠1=79°.
8.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.请问:AD平分∠BAC吗 若平分,请说明理由.
解:平分.理由:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°,∴AD∥EG,
∴∠3=∠2,∠E=∠1,∵∠3=∠E,∴∠1=∠2,即AD平分∠BAC.
9.如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( C )
A.45° B.60° C.90° D.120°
第9题图 第10题图 第11题图
10.【2022·宿迁】如图,AB∥ED,若∠1=70°,则∠2的度数是( D )
A.70° B.80° C.100° D.110°
11.【2022·娄底】一条古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( C )
A.20° B.80° C.100° D.120°
12.如图,∠B=∠C,∠A=∠D,有下列结论:
①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有( A )
A.①②④ B.②③④ C.③④ D.①②③④
第12题图 第13题图 第14题图
13.【2021·东营】如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( D )
A.30° B.40° C.50° D.60°
【点拨】如图,过点E作EG∥AB.
∵AB∥CD,∴EG∥CD,∴∠GEF+∠EFD=180°.
∵EF⊥CD,∴∠EFD=90°,
∴∠GEF=180°-∠EFD=90°.
∵∠BEF=∠BEG+∠GEF=150°,
∴∠BEG=∠BEF-∠GEF=60°.
∵EG∥AB,∴∠ABE=∠BEG=60°.
14.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( D )
A.110° B.115° C.120° D.125°
15.如图,∠1+∠2=180°,∠3=100°,则∠4等于 100° .
第15题图 第16题图 第17题图
16.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
【答案】110°
17.如图,∠1=∠2,∠A=60°,则∠ADC= 度.
【答案】120
18.【2022·太原五中模拟】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断BC与DE的位置关系,并说明理由;
解:(1)BC∥DE.理由如下:
∵∠1=80°,∠2=100°,∴∠1+∠2=180°.
∴BD∥CE.∴∠D=∠CEF.
∵∠C=∠D,∴∠C=∠CEF.∴BC∥DE .
(2)若∠A=35°,求∠F的度数.
由(1)知BC∥DE,∴∠A=∠F.
∵∠A=35°,∴∠F=35°.
19.【逻辑推理】如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试说明:CE∥GF;
解:(1)∵∠CED=∠GHD,∴CE∥GF.
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
∠AED+∠D=180°.理由如下:
∵CE∥GF,∴∠C=∠FGD.
∵∠C=∠EFG,∴∠FGD=∠EFG.
∴AB∥CD.∴∠AED+∠D=180°.
(3)若∠D=30°,求∠AED的度数.
由(2)知∠AED+∠D=180°.
∵∠D=30°,
∴∠AED=150°.
20.【2022·武汉】如图,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
解:(1)∵AD∥BC,
∴∠B+∠BAD=180°.
∵∠B=80°,∴∠BAD=100°.
(2)AE平分∠BAD交BC于点E,∠BCD=50°,试说明:AE∥DC.
由(1)知∠BAD=100°.
∵AE平分∠BAD,∴∠DAE=50°.
∵AD∥BC,∴∠AEB=∠DAE=50°.
∵∠BCD=50°,∴∠AEB=∠BCD.∴AE∥DC.
21.(1)如图1,已知∠B=25°,∠BED=80°,∠D=55°,探究AB与CD有怎样的位置关系;
(2)如图2,已知AB∥EF,试猜想∠B、∠F、∠BCF之间的关系,写出这种关系,并加以证明.
解:(1)AB∥CD.理由:过点E作EF∥AB,则∠BEF=∠B=25°,
∴∠DEF=80°-25°=55°=∠D,∴EF∥CD,∴AB∥CD;
(2)∠BCF=∠B+∠F.证明:过点C作CD∥AB.∵AB∥EF,CD∥AB,
∴AB∥CD∥EF,∴∠B=∠BCD,∠F=∠DCF,
∴∠BCF=∠BCD+∠DCF=∠B+∠F.
22.【阅读探究题】【探索】小明和小亮在研究一个数学问题:
如图,已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
【发现】小明和小亮都发现∠APC=∠A+∠C.
小明是这样解答的:如图,过点P在∠APC的内部作PQ∥AB,
∴∠APQ=∠A(__________________________).∵PQ∥AB,AB∥CD,∴PQ∥CD(__________________________________).
∴∠CPQ=∠C.∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
【答案】两直线平行,内错角相等 平行于同一条直线的两条直线平行
小亮是这样解答的:
如图,过点P作PQ∥AB∥CD,
∴∠APQ=∠A,∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面解答过程中的横线上填写依据.
两人的解答过程中,完全正确的是________.
【答案】小明
【应用】在图①中,AB∥CD,若∠A=120°,∠C=140°,则∠P的度数为________;在图②中,AB∥CD,若∠A=30°,∠C=70°,则∠P的度数为________.
【答案】100° 40°
【拓展】在图③中,AB∥CD,探索∠P与∠A,∠C的数量关系,并说明理由.
∠P=∠A-∠C.理由如下:
如图,过点P作PG∥AB,则∠APG+∠A=180°.
∴∠APG=180°-∠A.∵AB∥CD,PG∥AB,
∴PG∥CD.∴∠CPG+∠C=180°.
∴∠CPG=180°-∠C.
∴∠APC=∠CPG-∠APG=
180°-∠C-(180°-∠A)=∠A-∠C.
【点方法】利用平行线的性质求角的度数的方法:题目中出现两直线平行的条件时,应立即想到平行线的三个性质,要注意分析图形特征,明确角与角的位置关系,从而明确角与角之间的数量关系是相等还是互补.平行线还通常会与角平分线、垂线等知识结合,求角的度数有时需要根据已知条件综合利用角平分线、垂线的定义以及对顶角相等、邻补角互补等性质求解.
23.已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD.求证:∠AFC=∠AEC.
证明:分别过点E、F作ME∥AB,NF∥AB,∵∠EAF=∠EAB,∠ECF=∠ECD,设∠EAF=x,∠ECF=y,则∠EAB=4x,∠ECD=4y,故∠BAF=3x,∠DCF=3y,∵AB∥CD,ME∥AB,NF∥AB,∴AB∥ME∥NF∥CD,∴∠BAF=∠AFN=3x,∠BAE=∠AEM=4x,∠MEC=∠ECD=4y,∠NFC=∠FCD=3y,∴∠AEC=∠AEM+∠MEC=4(x+y),∠AFC=∠AFN+∠NFC=3(x+y),∴∠AFC=∠AEC.
5.3.1 平行线的性质
第2课时 平行线的判定和性质的综合应用
1.如图,直线a、b被直线c、d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数为( )
A.80° B.85° C.95° D.100°
第1题图 第2题图 第3题图
2.如图,a、b、c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为( )
A.70° B.90° C.110° D.80°
3.如图,由A到B的方向是( )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
4.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
第4题图 第5题图 第6题图
5.如图,已知AB∥CD,则∠BAE+∠AEF+∠EFC+∠FCD的度数为 .
6.一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
7.如图,已知四条直线a、b、c、d,∠1=79°,∠2=79°,∠3=101°.指出图中有哪些直线平行?说明理由,并求出α的度数.
8.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.请问:AD平分∠BAC吗 若平分,请说明理由.
9.如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( )
A.45° B.60° C.90° D.120°
第9题图 第10题图 第11题图
10.【2022·宿迁】如图,AB∥ED,若∠1=70°,则∠2的度数是( )
A.70° B.80° C.100° D.110°
11.【2022·娄底】一条古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( )
A.20° B.80° C.100° D.120°
12.如图,∠B=∠C,∠A=∠D,有下列结论:
①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有( )
A.①②④ B.②③④ C.③④ D.①②③④
第12题图 第13题图 第14题图
13.【2021·东营】如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( )
A.30° B.40° C.50° D.60°
14.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( )
A.110° B.115° C.120° D.125°
15.如图,∠1+∠2=180°,∠3=100°,则∠4等于 .
第15题图 第16题图 第17题图
16.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
17.如图,∠1=∠2,∠A=60°,则∠ADC= 度.
18.【2022·太原五中模拟】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断BC与DE的位置关系,并说明理由;
(2)若∠A=35°,求∠F的度数.
19.【逻辑推理】如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试说明:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠D=30°,求∠AED的度数.
20.【2022·武汉】如图,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
(2)AE平分∠BAD交BC于点E,∠BCD=50°,试说明:AE∥DC.
21.(1)如图1,已知∠B=25°,∠BED=80°,∠D=55°,探究AB与CD有怎样的位置关系;
(2)如图2,已知AB∥EF,试猜想∠B、∠F、∠BCF之间的关系,写出这种关系,并加以证明.
22.【阅读探究题】【探索】小明和小亮在研究一个数学问题:
如图,已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
【发现】小明和小亮都发现∠APC=∠A+∠C.
小明是这样解答的:如图,过点P在∠APC的内部作PQ∥AB,
∴∠APQ=∠A(__________________________).∵PQ∥AB,AB∥CD,∴PQ∥CD(__________________________________).
∴∠CPQ=∠C.∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
小亮是这样解答的:
如图,过点P作PQ∥AB∥CD,
∴∠APQ=∠A,∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面解答过程中的横线上填写依据.
两人的解答过程中,完全正确的是________.
【应用】在图①中,AB∥CD,若∠A=120°,∠C=140°,则∠P的度数为________;在图②中,AB∥CD,若∠A=30°,∠C=70°,则∠P的度数为________.
【拓展】在图③中,AB∥CD,探索∠P与∠A,∠C的数量关系,并说明理由.
23.已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD.求证:∠AFC=∠AEC.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.如图,直线a、b被直线c、d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数为( B )
A.80° B.85° C.95° D.100°
第1题图 第2题图 第3题图
2.如图,a、b、c为三条直线,且a⊥c,b⊥c,若∠1=70°,则∠2的度数为( A )
A.70° B.90° C.110° D.80°
3.如图,由A到B的方向是( B )
A.南偏东30° B.南偏东60° C.北偏西30° D.北偏西60°
4.如图,已知两直线l1与l2被第三条直线l3所截,下列等式一定成立的是( D )
A.∠1=∠2 B.∠2=∠3 C.∠2+∠4=180° D.∠1+∠4=180°
第4题图 第5题图 第6题图
5.如图,已知AB∥CD,则∠BAE+∠AEF+∠EFC+∠FCD的度数为
【答案】540°
6.一大门的栏杆如图所示,BA垂直地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= .
【答案】270°
7.如图,已知四条直线a、b、c、d,∠1=79°,∠2=79°,∠3=101°.指出图中有哪些直线平行?说明理由,并求出α的度数.
解:a∥b,c∥d,∵∠2=∠1=79°,∴a∥b,又∠4=∠3=101°,∴∠2+∠4=180°,∴c∥d,∴∠α=∠1=79°.
8.如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3.请问:AD平分∠BAC吗 若平分,请说明理由.
解:平分.理由:∵AD⊥BC,EG⊥BC,
∴∠ADC=∠EGC=90°,∴AD∥EG,
∴∠3=∠2,∠E=∠1,∵∠3=∠E,∴∠1=∠2,即AD平分∠BAC.
9.如图,直线a∥b,c⊥a,则c与b相交所形成的∠1的度数为( C )
A.45° B.60° C.90° D.120°
第9题图 第10题图 第11题图
10.【2022·宿迁】如图,AB∥ED,若∠1=70°,则∠2的度数是( D )
A.70° B.80° C.100° D.110°
11.【2022·娄底】一条古秤在称物时的状态如图所示,已知∠1=80°,则∠2=( C )
A.20° B.80° C.100° D.120°
12.如图,∠B=∠C,∠A=∠D,有下列结论:
①AB∥CD;②AE∥DF;③AE⊥BC;④∠AMC=∠BND.
其中正确的有( A )
A.①②④ B.②③④ C.③④ D.①②③④
第12题图 第13题图 第14题图
13.【2021·东营】如图,AB∥CD,EF⊥CD于点F,若∠BEF=150°,则∠ABE=( D )
A.30° B.40° C.50° D.60°
【点拨】如图,过点E作EG∥AB.
∵AB∥CD,∴EG∥CD,∴∠GEF+∠EFD=180°.
∵EF⊥CD,∴∠EFD=90°,
∴∠GEF=180°-∠EFD=90°.
∵∠BEF=∠BEG+∠GEF=150°,
∴∠BEG=∠BEF-∠GEF=60°.
∵EG∥AB,∴∠ABE=∠BEG=60°.
14.如图,已知∠1=∠2=∠3=55°,则∠4的度数是( D )
A.110° B.115° C.120° D.125°
15.如图,∠1+∠2=180°,∠3=100°,则∠4等于 100° .
第15题图 第16题图 第17题图
16.如图,若∠1+∠2=180°,∠3=110°,则∠4= .
【答案】110°
17.如图,∠1=∠2,∠A=60°,则∠ADC= 度.
【答案】120
18.【2022·太原五中模拟】如图,∠1=80°,∠2=100°,∠C=∠D.
(1)判断BC与DE的位置关系,并说明理由;
解:(1)BC∥DE.理由如下:
∵∠1=80°,∠2=100°,∴∠1+∠2=180°.
∴BD∥CE.∴∠D=∠CEF.
∵∠C=∠D,∴∠C=∠CEF.∴BC∥DE .
(2)若∠A=35°,求∠F的度数.
由(1)知BC∥DE,∴∠A=∠F.
∵∠A=35°,∴∠F=35°.
19.【逻辑推理】如图,已知点E,F在直线AB上,点G在线段CD上,ED与FG相交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)试说明:CE∥GF;
解:(1)∵∠CED=∠GHD,∴CE∥GF.
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
∠AED+∠D=180°.理由如下:
∵CE∥GF,∴∠C=∠FGD.
∵∠C=∠EFG,∴∠FGD=∠EFG.
∴AB∥CD.∴∠AED+∠D=180°.
(3)若∠D=30°,求∠AED的度数.
由(2)知∠AED+∠D=180°.
∵∠D=30°,
∴∠AED=150°.
20.【2022·武汉】如图,在四边形ABCD中,AD∥BC,∠B=80°.
(1)求∠BAD的度数;
解:(1)∵AD∥BC,
∴∠B+∠BAD=180°.
∵∠B=80°,∴∠BAD=100°.
(2)AE平分∠BAD交BC于点E,∠BCD=50°,试说明:AE∥DC.
由(1)知∠BAD=100°.
∵AE平分∠BAD,∴∠DAE=50°.
∵AD∥BC,∴∠AEB=∠DAE=50°.
∵∠BCD=50°,∴∠AEB=∠BCD.∴AE∥DC.
21.(1)如图1,已知∠B=25°,∠BED=80°,∠D=55°,探究AB与CD有怎样的位置关系;
(2)如图2,已知AB∥EF,试猜想∠B、∠F、∠BCF之间的关系,写出这种关系,并加以证明.
解:(1)AB∥CD.理由:过点E作EF∥AB,则∠BEF=∠B=25°,
∴∠DEF=80°-25°=55°=∠D,∴EF∥CD,∴AB∥CD;
(2)∠BCF=∠B+∠F.证明:过点C作CD∥AB.∵AB∥EF,CD∥AB,
∴AB∥CD∥EF,∴∠B=∠BCD,∠F=∠DCF,
∴∠BCF=∠BCD+∠DCF=∠B+∠F.
22.【阅读探究题】【探索】小明和小亮在研究一个数学问题:
如图,已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
【发现】小明和小亮都发现∠APC=∠A+∠C.
小明是这样解答的:如图,过点P在∠APC的内部作PQ∥AB,
∴∠APQ=∠A(__________________________).∵PQ∥AB,AB∥CD,∴PQ∥CD(__________________________________).
∴∠CPQ=∠C.∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
【答案】两直线平行,内错角相等 平行于同一条直线的两条直线平行
小亮是这样解答的:
如图,过点P作PQ∥AB∥CD,
∴∠APQ=∠A,∠CPQ=∠C.
∴∠APQ+∠CPQ=∠A+∠C,
即∠APC=∠A+∠C.
请在上面解答过程中的横线上填写依据.
两人的解答过程中,完全正确的是________.
【答案】小明
【应用】在图①中,AB∥CD,若∠A=120°,∠C=140°,则∠P的度数为________;在图②中,AB∥CD,若∠A=30°,∠C=70°,则∠P的度数为________.
【答案】100° 40°
【拓展】在图③中,AB∥CD,探索∠P与∠A,∠C的数量关系,并说明理由.
∠P=∠A-∠C.理由如下:
如图,过点P作PG∥AB,则∠APG+∠A=180°.
∴∠APG=180°-∠A.∵AB∥CD,PG∥AB,
∴PG∥CD.∴∠CPG+∠C=180°.
∴∠CPG=180°-∠C.
∴∠APC=∠CPG-∠APG=
180°-∠C-(180°-∠A)=∠A-∠C.
【点方法】利用平行线的性质求角的度数的方法:题目中出现两直线平行的条件时,应立即想到平行线的三个性质,要注意分析图形特征,明确角与角的位置关系,从而明确角与角之间的数量关系是相等还是互补.平行线还通常会与角平分线、垂线等知识结合,求角的度数有时需要根据已知条件综合利用角平分线、垂线的定义以及对顶角相等、邻补角互补等性质求解.
23.已知AB∥CD,∠EAF=∠EAB,∠ECF=∠ECD.求证:∠AFC=∠AEC.
证明:分别过点E、F作ME∥AB,NF∥AB,∵∠EAF=∠EAB,∠ECF=∠ECD,设∠EAF=x,∠ECF=y,则∠EAB=4x,∠ECD=4y,故∠BAF=3x,∠DCF=3y,∵AB∥CD,ME∥AB,NF∥AB,∴AB∥ME∥NF∥CD,∴∠BAF=∠AFN=3x,∠BAE=∠AEM=4x,∠MEC=∠ECD=4y,∠NFC=∠FCD=3y,∴∠AEC=∠AEM+∠MEC=4(x+y),∠AFC=∠AFN+∠NFC=3(x+y),∴∠AFC=∠AEC.
