5.3.2 命题、定理、证明 同步练习(含答案)
文档属性
| 名称 | 5.3.2 命题、定理、证明 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 00:00:00 | ||
图片预览




文档简介
5.3 平行线的性质
5.3.2 命题、定理、证明
1.下列语句中,是命题的是( )
A.有公共顶点的两个角是对顶角 B.作∠A的平分线
C.用量角器量角的度数 D.直角都相等吗
2.命题“等角的补角相等”的题设是( )
A.等角 B.这两个角相等 C.补角相等 D.两个角是等角的补角
3.下列命题中,是真命题的是( )
A.同位角相等 B.同旁内角互补
C.经过一点有且只有一条直线与已知直线平行
D.同一平面内,两条直线的位置关系只有相交和平行
4.下列命题中,属于假命题的是( )
A.若a-b=0,则a=b=0 B.若a-b>0,则a>b
C.若a-b<0,则a<b D.若a-b≠0,则a≠b
5.下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=-2 B.a=-1 C.a=1 D.a=2
6.(1) 的语句叫做命题.命题是由 和 两部分组成,题设是 ,结论是 .
(2)如果题设成立,那么结论一定成立的命题叫做 ;如果题设成立,但
的命题叫做假命题.
(3)有一些命题,它的正确性是经过 证实的,这样的真命题叫定理,一个命题的正确性需要经过推理,方能作出判断,这个 过程叫证明.
7.两个锐角的和是钝角写成“如果……,那么……”的形式为 .
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
解:∵AB∥DC(已知),∴∠1=∠CFE( ).∵AE平分∠BAD(已知),∴∠1=∠2 (角平分线的定义).∵∠CFE=∠E(已知),∴∠2= (等量代换).∴AD∥BC ( ).
9.命题“对顶角相等”的“题设”是( )
A.两个角是对顶角 B.角是对顶角 C.对顶角 D.以上都不正确
10.命题“平行于同一条直线的两条直线平行”的题设是( )
A.平行 B.两条直线 C.同一条直线 D.两条直线平行于同一条直线
11.【2022·梧州】下列命题中,假命题是( )
A.-2的绝对值是-2 B.对顶角相等
C.两点确定一条直线 D.如果直线a∥c,b∥c,那么直线a∥b
12.下列命题可以作为定理的有( )
①两直线平行,同旁内角互补;②相等的角是对顶角;
③等角的余角相等;④对顶角相等.
A.1个 B.2个 C.3个 D.4个
13.【2021·荆州】阅读下列材料,①~④步中数学依据错误的是( )
如图:已知直线b∥c,a⊥b,求证:a⊥c.
证明:①∵a⊥b(已知),
∴∠1=90°(垂直的定义).
②又∵b∥c(已知),
∴∠1=∠2(同位角相等,两直线平行).
③∴∠2=∠1=90°(等量代换).
④∴a⊥c(垂直的定义).
A.① B.② C.③ D.④
14.【中考·宜昌】能说明“锐角α、锐角β的和是锐角”是假命题的例证图是( )
15.若a=b,则a2=b2,它是 真 命题(填“真”或“假”),其中a=b是 ,a2=b2是 .
16.对于同一平面内的三条直线a、b、c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题: (用序号写出一个即可).
17.【2022·长沙一中模拟】推理填空:
如图,已知∠1=∠2,∠B=∠C.求证:AB∥CD.
证明:∵∠1=∠2(已知),且∠1=∠4(___________),
∴∠2=∠4(等量代换).∴CE∥BF(________________________).
∴∠______=∠3(_________________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(______________________________).
18.判断下列命题是真命题还是假命题,如果是假命题,请举一反例说明.
(1)如果ac=bc,那么a=b;
(2)在同一平面内,经过一点有且只有一条直线垂直于已知直线;
(3)如果a2=b2,那么a=b.
19.(1)如图,DE∥BC,∠1=∠3,CD⊥AB.求证:FG⊥AB.
(2)若把(1)题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由.
(3)若把(1)题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
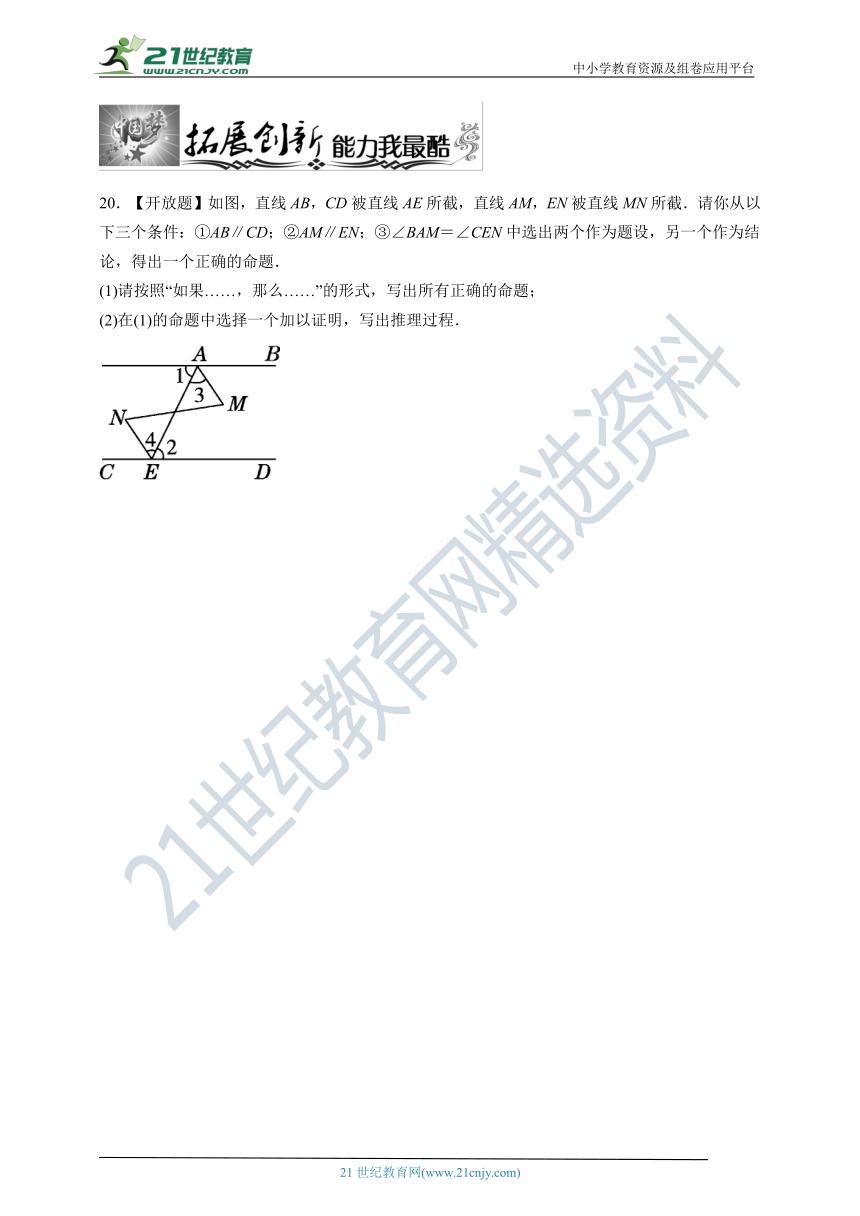
20.【开放题】如图,直线AB,CD被直线AE所截,直线AM,EN被直线MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为题设,另一个作为结论,得出一个正确的命题.
(1)请按照“如果……,那么……”的形式,写出所有正确的命题;
(2)在(1)的命题中选择一个加以证明,写出推理过程.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列语句中,是命题的是( A )
A.有公共顶点的两个角是对顶角 B.作∠A的平分线
C.用量角器量角的度数 D.直角都相等吗
2.命题“等角的补角相等”的题设是( D )
A.等角 B.这两个角相等 C.补角相等 D.两个角是等角的补角
3.下列命题中,是真命题的是( D )
A.同位角相等 B.同旁内角互补
C.经过一点有且只有一条直线与已知直线平行
D.同一平面内,两条直线的位置关系只有相交和平行
4.下列命题中,属于假命题的是( A )
A.若a-b=0,则a=b=0 B.若a-b>0,则a>b
C.若a-b<0,则a<b D.若a-b≠0,则a≠b
5.下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( A )
A.a=-2 B.a=-1 C.a=1 D.a=2
6.(1) 的语句叫做命题.命题是由 和 两部分组成,题设是 ,结论是 .
【答案】判断一件事件 题设 结论 已知事项 由已知事项推出的事项
(2)如果题设成立,那么结论一定成立的命题叫做 ;如果题设成立,但 的命题叫做假命题.
【答案】真命题 结论不一定成立
(3)有一些命题,它的正确性是经过 证实的,这样的真命题叫定理,一个命题的正确性需要经过推理,方能作出判断,这个 过程叫证明.
【答案】推理 推理
7.两个锐角的和是钝角写成“如果……,那么……”的形式为 .
【答案】如果两个角是锐角,那么它们的和为钝角
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
解:∵AB∥DC(已知),∴∠1=∠CFE( ).∵AE平分∠BAD(已知),∴∠1=∠2 (角平分线的定义).∵∠CFE=∠E(已知),∴∠2= (等量代换).∴AD∥BC ( ).
【答案】两直线平行,同位角相等 ∠E 内错角相等,两直线平行
9.命题“对顶角相等”的“题设”是( A )
A.两个角是对顶角 B.角是对顶角 C.对顶角 D.以上都不正确
10.命题“平行于同一条直线的两条直线平行”的题设是( D )
A.平行 B.两条直线 C.同一条直线 D.两条直线平行于同一条直线
11.【2022·梧州】下列命题中,假命题是( A )
A.-2的绝对值是-2 B.对顶角相等
C.两点确定一条直线 D.如果直线a∥c,b∥c,那么直线a∥b
12.下列命题可以作为定理的有( C )
①两直线平行,同旁内角互补;②相等的角是对顶角;
③等角的余角相等;④对顶角相等.
A.1个 B.2个 C.3个 D.4个
13.【2021·荆州】阅读下列材料,①~④步中数学依据错误的是( B )
如图:已知直线b∥c,a⊥b,求证:a⊥c.
证明:①∵a⊥b(已知),
∴∠1=90°(垂直的定义).
②又∵b∥c(已知),
∴∠1=∠2(同位角相等,两直线平行).
③∴∠2=∠1=90°(等量代换).
④∴a⊥c(垂直的定义).
A.① B.② C.③ D.④
14.【中考·宜昌】能说明“锐角α、锐角β的和是锐角”是假命题的例证图是( C )
15.若a=b,则a2=b2,它是 真 命题(填“真”或“假”),其中a=b是 题设 ,a2=b2是 结论 .
16.对于同一平面内的三条直线a、b、c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题: ①② ④,②③ ⑤等(答案不唯一) (用序号写出一个即可).
17.【2022·长沙一中模拟】推理填空:
如图,已知∠1=∠2,∠B=∠C.求证:AB∥CD.
证明:∵∠1=∠2(已知),且∠1=∠4(___________),
∴∠2=∠4(等量代换).∴CE∥BF(________________________).
∴∠______=∠3(_________________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(______________________________).
【答案】对顶角相等
同位角相等,两直线平行
C 两直线平行,同位角相等
内错角相等,两直线平行
18.判断下列命题是真命题还是假命题,如果是假命题,请举一反例说明.
(1)如果ac=bc,那么a=b;
解:(1)是假命题,例如:3×0=2×0,但3≠2;
(2)在同一平面内,经过一点有且只有一条直线垂直于已知直线;
(2)是真命题;
(3)如果a2=b2,那么a=b.
(3)是假命题,例如:(-2)2=22,但-2≠2.
19.(1)如图,DE∥BC,∠1=∠3,CD⊥AB.求证:FG⊥AB.
证明:∵DE∥BC,∴∠1=∠2.
又∵∠1=∠3,∴∠2=∠3.
∴CD∥FG.∴∠BFG=∠CDB.
∵CD⊥AB,∴∠CDB=90°.
∴∠BFG=90°.∴FG⊥AB.
(2)若把(1)题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由.
解:是真命题.理由如下:
∵CD⊥AB,FG⊥AB,∴CD∥FG.
∴∠2=∠3.
又∵∠1=∠3,∴∠1=∠2.
∴DE∥BC.
(3)若把(1)题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
解:是真命题.理由如下:
同(2)可得∠2=∠3.
∵DE∥BC,∴∠1=∠2.
∴∠1=∠3.
20.【开放题】如图,直线AB,CD被直线AE所截,直线AM,EN被直线MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为题设,另一个作为结论,得出一个正确的命题.
(1)请按照“如果……,那么……”的形式,写出所有正确的命题;
解:a.如果AB∥CD,AM∥EN,
那么∠BAM=∠CEN.
b.如果AB∥CD,∠BAM=∠CEN,
那么AM∥EN.
c.如果AM∥EN,∠BAM=∠CEN,
那么AB∥CD.
(2)在(1)的命题中选择一个加以证明,写出推理过程.
证明:(答案不唯一,选择命题a)
∵AB∥CD,∴∠BAE=∠CEA.
∵AM∥EN,∴∠3=∠4.
∴∠BAE-∠3=∠CEA-∠4,
即∠BAM=∠CEN.
【点方法】证明一个命题的一般步骤:
1 . 分清命题的题设和结论,如果与图形有关,首先根据题意, 画出图形, 并在图形上标出有关字母与符号;
2 . 根据题设、结论,结合图形,写出已知、求证;
3 . 经过分析,找出由已知推出结论的途径,有条理地写出证明过程.
5.3.2 命题、定理、证明
1.下列语句中,是命题的是( )
A.有公共顶点的两个角是对顶角 B.作∠A的平分线
C.用量角器量角的度数 D.直角都相等吗
2.命题“等角的补角相等”的题设是( )
A.等角 B.这两个角相等 C.补角相等 D.两个角是等角的补角
3.下列命题中,是真命题的是( )
A.同位角相等 B.同旁内角互补
C.经过一点有且只有一条直线与已知直线平行
D.同一平面内,两条直线的位置关系只有相交和平行
4.下列命题中,属于假命题的是( )
A.若a-b=0,则a=b=0 B.若a-b>0,则a>b
C.若a-b<0,则a<b D.若a-b≠0,则a≠b
5.下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( )
A.a=-2 B.a=-1 C.a=1 D.a=2
6.(1) 的语句叫做命题.命题是由 和 两部分组成,题设是 ,结论是 .
(2)如果题设成立,那么结论一定成立的命题叫做 ;如果题设成立,但
的命题叫做假命题.
(3)有一些命题,它的正确性是经过 证实的,这样的真命题叫定理,一个命题的正确性需要经过推理,方能作出判断,这个 过程叫证明.
7.两个锐角的和是钝角写成“如果……,那么……”的形式为 .
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
解:∵AB∥DC(已知),∴∠1=∠CFE( ).∵AE平分∠BAD(已知),∴∠1=∠2 (角平分线的定义).∵∠CFE=∠E(已知),∴∠2= (等量代换).∴AD∥BC ( ).
9.命题“对顶角相等”的“题设”是( )
A.两个角是对顶角 B.角是对顶角 C.对顶角 D.以上都不正确
10.命题“平行于同一条直线的两条直线平行”的题设是( )
A.平行 B.两条直线 C.同一条直线 D.两条直线平行于同一条直线
11.【2022·梧州】下列命题中,假命题是( )
A.-2的绝对值是-2 B.对顶角相等
C.两点确定一条直线 D.如果直线a∥c,b∥c,那么直线a∥b
12.下列命题可以作为定理的有( )
①两直线平行,同旁内角互补;②相等的角是对顶角;
③等角的余角相等;④对顶角相等.
A.1个 B.2个 C.3个 D.4个
13.【2021·荆州】阅读下列材料,①~④步中数学依据错误的是( )
如图:已知直线b∥c,a⊥b,求证:a⊥c.
证明:①∵a⊥b(已知),
∴∠1=90°(垂直的定义).
②又∵b∥c(已知),
∴∠1=∠2(同位角相等,两直线平行).
③∴∠2=∠1=90°(等量代换).
④∴a⊥c(垂直的定义).
A.① B.② C.③ D.④
14.【中考·宜昌】能说明“锐角α、锐角β的和是锐角”是假命题的例证图是( )
15.若a=b,则a2=b2,它是 真 命题(填“真”或“假”),其中a=b是 ,a2=b2是 .
16.对于同一平面内的三条直线a、b、c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题: (用序号写出一个即可).
17.【2022·长沙一中模拟】推理填空:
如图,已知∠1=∠2,∠B=∠C.求证:AB∥CD.
证明:∵∠1=∠2(已知),且∠1=∠4(___________),
∴∠2=∠4(等量代换).∴CE∥BF(________________________).
∴∠______=∠3(_________________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(______________________________).
18.判断下列命题是真命题还是假命题,如果是假命题,请举一反例说明.
(1)如果ac=bc,那么a=b;
(2)在同一平面内,经过一点有且只有一条直线垂直于已知直线;
(3)如果a2=b2,那么a=b.
19.(1)如图,DE∥BC,∠1=∠3,CD⊥AB.求证:FG⊥AB.
(2)若把(1)题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由.
(3)若把(1)题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
20.【开放题】如图,直线AB,CD被直线AE所截,直线AM,EN被直线MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为题设,另一个作为结论,得出一个正确的命题.
(1)请按照“如果……,那么……”的形式,写出所有正确的命题;
(2)在(1)的命题中选择一个加以证明,写出推理过程.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列语句中,是命题的是( A )
A.有公共顶点的两个角是对顶角 B.作∠A的平分线
C.用量角器量角的度数 D.直角都相等吗
2.命题“等角的补角相等”的题设是( D )
A.等角 B.这两个角相等 C.补角相等 D.两个角是等角的补角
3.下列命题中,是真命题的是( D )
A.同位角相等 B.同旁内角互补
C.经过一点有且只有一条直线与已知直线平行
D.同一平面内,两条直线的位置关系只有相交和平行
4.下列命题中,属于假命题的是( A )
A.若a-b=0,则a=b=0 B.若a-b>0,则a>b
C.若a-b<0,则a<b D.若a-b≠0,则a≠b
5.下列选项中,可以用来证明命题“若a2>1,则a>1”是假命题的反例是( A )
A.a=-2 B.a=-1 C.a=1 D.a=2
6.(1) 的语句叫做命题.命题是由 和 两部分组成,题设是 ,结论是 .
【答案】判断一件事件 题设 结论 已知事项 由已知事项推出的事项
(2)如果题设成立,那么结论一定成立的命题叫做 ;如果题设成立,但 的命题叫做假命题.
【答案】真命题 结论不一定成立
(3)有一些命题,它的正确性是经过 证实的,这样的真命题叫定理,一个命题的正确性需要经过推理,方能作出判断,这个 过程叫证明.
【答案】推理 推理
7.两个锐角的和是钝角写成“如果……,那么……”的形式为 .
【答案】如果两个角是锐角,那么它们的和为钝角
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
解:∵AB∥DC(已知),∴∠1=∠CFE( ).∵AE平分∠BAD(已知),∴∠1=∠2 (角平分线的定义).∵∠CFE=∠E(已知),∴∠2= (等量代换).∴AD∥BC ( ).
【答案】两直线平行,同位角相等 ∠E 内错角相等,两直线平行
9.命题“对顶角相等”的“题设”是( A )
A.两个角是对顶角 B.角是对顶角 C.对顶角 D.以上都不正确
10.命题“平行于同一条直线的两条直线平行”的题设是( D )
A.平行 B.两条直线 C.同一条直线 D.两条直线平行于同一条直线
11.【2022·梧州】下列命题中,假命题是( A )
A.-2的绝对值是-2 B.对顶角相等
C.两点确定一条直线 D.如果直线a∥c,b∥c,那么直线a∥b
12.下列命题可以作为定理的有( C )
①两直线平行,同旁内角互补;②相等的角是对顶角;
③等角的余角相等;④对顶角相等.
A.1个 B.2个 C.3个 D.4个
13.【2021·荆州】阅读下列材料,①~④步中数学依据错误的是( B )
如图:已知直线b∥c,a⊥b,求证:a⊥c.
证明:①∵a⊥b(已知),
∴∠1=90°(垂直的定义).
②又∵b∥c(已知),
∴∠1=∠2(同位角相等,两直线平行).
③∴∠2=∠1=90°(等量代换).
④∴a⊥c(垂直的定义).
A.① B.② C.③ D.④
14.【中考·宜昌】能说明“锐角α、锐角β的和是锐角”是假命题的例证图是( C )
15.若a=b,则a2=b2,它是 真 命题(填“真”或“假”),其中a=b是 题设 ,a2=b2是 结论 .
16.对于同一平面内的三条直线a、b、c,给出下列五个论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题: ①② ④,②③ ⑤等(答案不唯一) (用序号写出一个即可).
17.【2022·长沙一中模拟】推理填空:
如图,已知∠1=∠2,∠B=∠C.求证:AB∥CD.
证明:∵∠1=∠2(已知),且∠1=∠4(___________),
∴∠2=∠4(等量代换).∴CE∥BF(________________________).
∴∠______=∠3(_________________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(______________________________).
【答案】对顶角相等
同位角相等,两直线平行
C 两直线平行,同位角相等
内错角相等,两直线平行
18.判断下列命题是真命题还是假命题,如果是假命题,请举一反例说明.
(1)如果ac=bc,那么a=b;
解:(1)是假命题,例如:3×0=2×0,但3≠2;
(2)在同一平面内,经过一点有且只有一条直线垂直于已知直线;
(2)是真命题;
(3)如果a2=b2,那么a=b.
(3)是假命题,例如:(-2)2=22,但-2≠2.
19.(1)如图,DE∥BC,∠1=∠3,CD⊥AB.求证:FG⊥AB.
证明:∵DE∥BC,∴∠1=∠2.
又∵∠1=∠3,∴∠2=∠3.
∴CD∥FG.∴∠BFG=∠CDB.
∵CD⊥AB,∴∠CDB=90°.
∴∠BFG=90°.∴FG⊥AB.
(2)若把(1)题设中的“DE∥BC”与结论“FG⊥AB”对调,所得命题是否为真命题?试说明理由.
解:是真命题.理由如下:
∵CD⊥AB,FG⊥AB,∴CD∥FG.
∴∠2=∠3.
又∵∠1=∠3,∴∠1=∠2.
∴DE∥BC.
(3)若把(1)题设中的“∠1=∠3”与结论“FG⊥AB”对调呢?
解:是真命题.理由如下:
同(2)可得∠2=∠3.
∵DE∥BC,∴∠1=∠2.
∴∠1=∠3.
20.【开放题】如图,直线AB,CD被直线AE所截,直线AM,EN被直线MN所截.请你从以下三个条件:①AB∥CD;②AM∥EN;③∠BAM=∠CEN中选出两个作为题设,另一个作为结论,得出一个正确的命题.
(1)请按照“如果……,那么……”的形式,写出所有正确的命题;
解:a.如果AB∥CD,AM∥EN,
那么∠BAM=∠CEN.
b.如果AB∥CD,∠BAM=∠CEN,
那么AM∥EN.
c.如果AM∥EN,∠BAM=∠CEN,
那么AB∥CD.
(2)在(1)的命题中选择一个加以证明,写出推理过程.
证明:(答案不唯一,选择命题a)
∵AB∥CD,∴∠BAE=∠CEA.
∵AM∥EN,∴∠3=∠4.
∴∠BAE-∠3=∠CEA-∠4,
即∠BAM=∠CEN.
【点方法】证明一个命题的一般步骤:
1 . 分清命题的题设和结论,如果与图形有关,首先根据题意, 画出图形, 并在图形上标出有关字母与符号;
2 . 根据题设、结论,结合图形,写出已知、求证;
3 . 经过分析,找出由已知推出结论的途径,有条理地写出证明过程.
