5.4 平移 同步练习(含答案)
图片预览

文档简介
5.4 平移
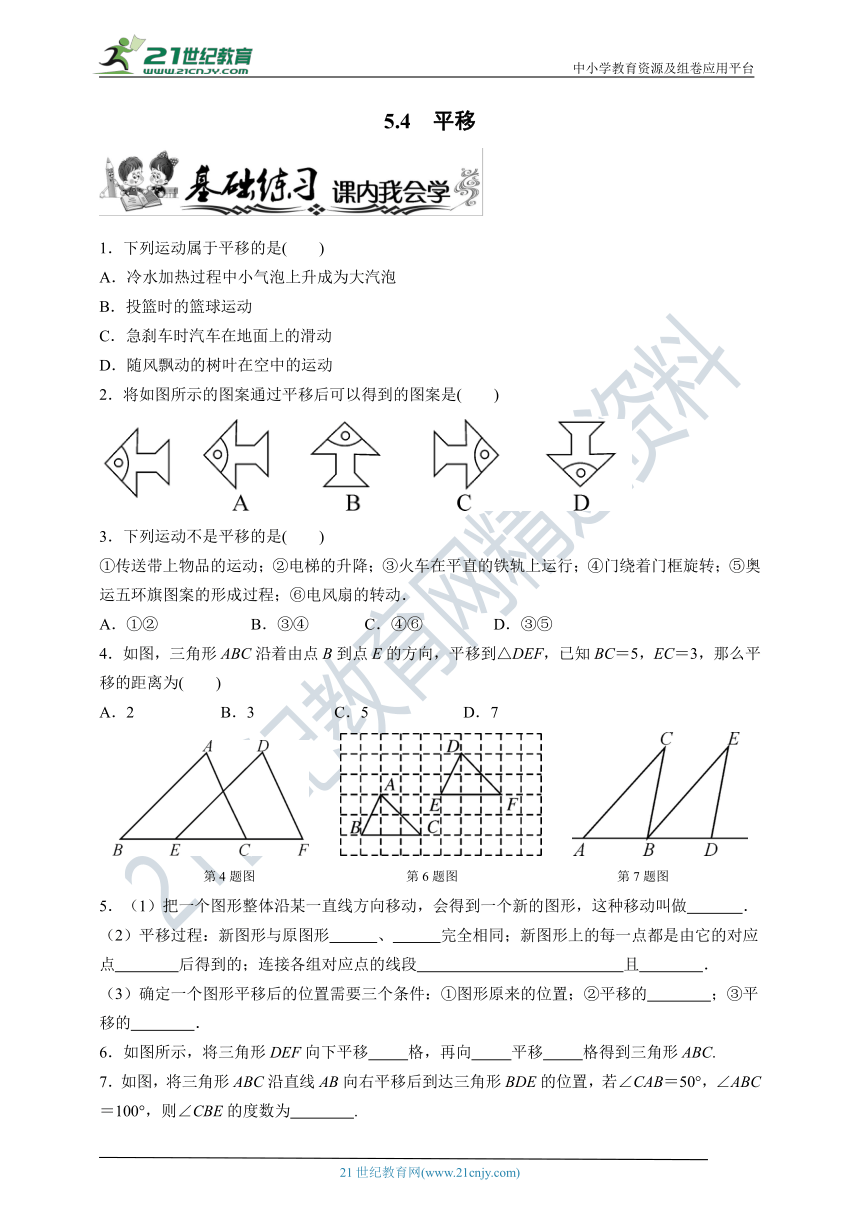
1.下列运动属于平移的是( )
A.冷水加热过程中小气泡上升成为大汽泡
B.投篮时的篮球运动
C.急刹车时汽车在地面上的滑动
D.随风飘动的树叶在空中的运动
2.将如图所示的图案通过平移后可以得到的图案是( )
3.下列运动不是平移的是( )
①传送带上物品的运动;②电梯的升降;③火车在平直的铁轨上运行;④门绕着门框旋转;⑤奥运五环旗图案的形成过程;⑥电风扇的转动.
A.①② B.③④ C.④⑥ D.③⑤
4.如图,三角形ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5,EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.7
第4题图 第6题图 第7题图
5.(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,这种移动叫做 .
(2)平移过程:新图形与原图形 、 完全相同;新图形上的每一点都是由它的对应点 后得到的;连接各组对应点的线段 且 .
(3)确定一个图形平移后的位置需要三个条件:①图形原来的位置;②平移的 ;③平移的 .
6.如图所示,将三角形DEF向下平移 格,再向 平移 格得到三角形ABC.
7.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
8.如图,三角形ABC是通过平移三角形DEF得到的,已知ED和BA是对应线段,请在图中画出三角形DEF.
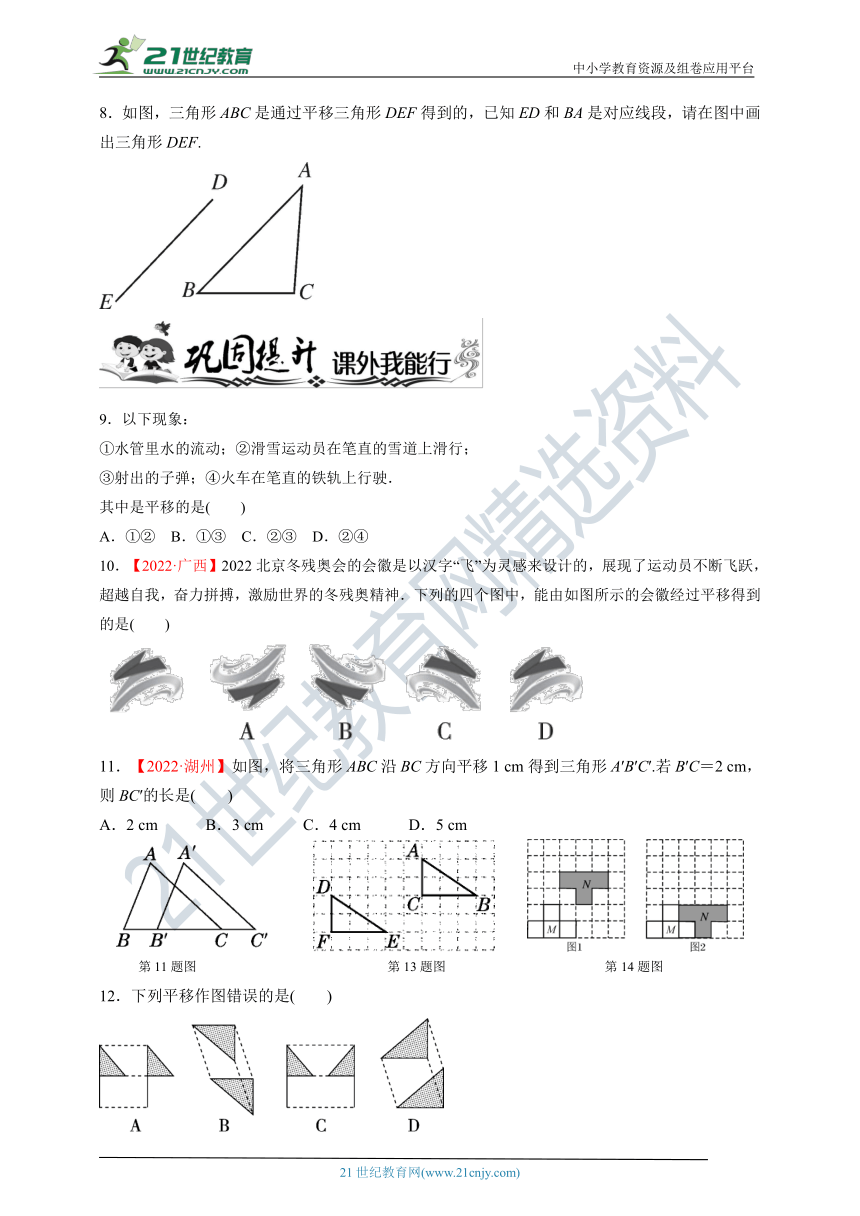
9.以下现象:
①水管里水的流动;②滑雪运动员在笔直的雪道上滑行;
③射出的子弹;④火车在笔直的铁轨上行驶.
其中是平移的是( )
A.①② B.①③ C.②③ D.②④
10.【2022·广西】2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
11.【2022·湖州】如图,将三角形ABC沿BC方向平移1 cm得到三角形A′B′C′.若B′C=2 cm,则BC′的长是( )
A.2 cm B.3 cm C.4 cm D.5 cm
第11题图 第13题图 第14题图
12.下列平移作图错误的是( )
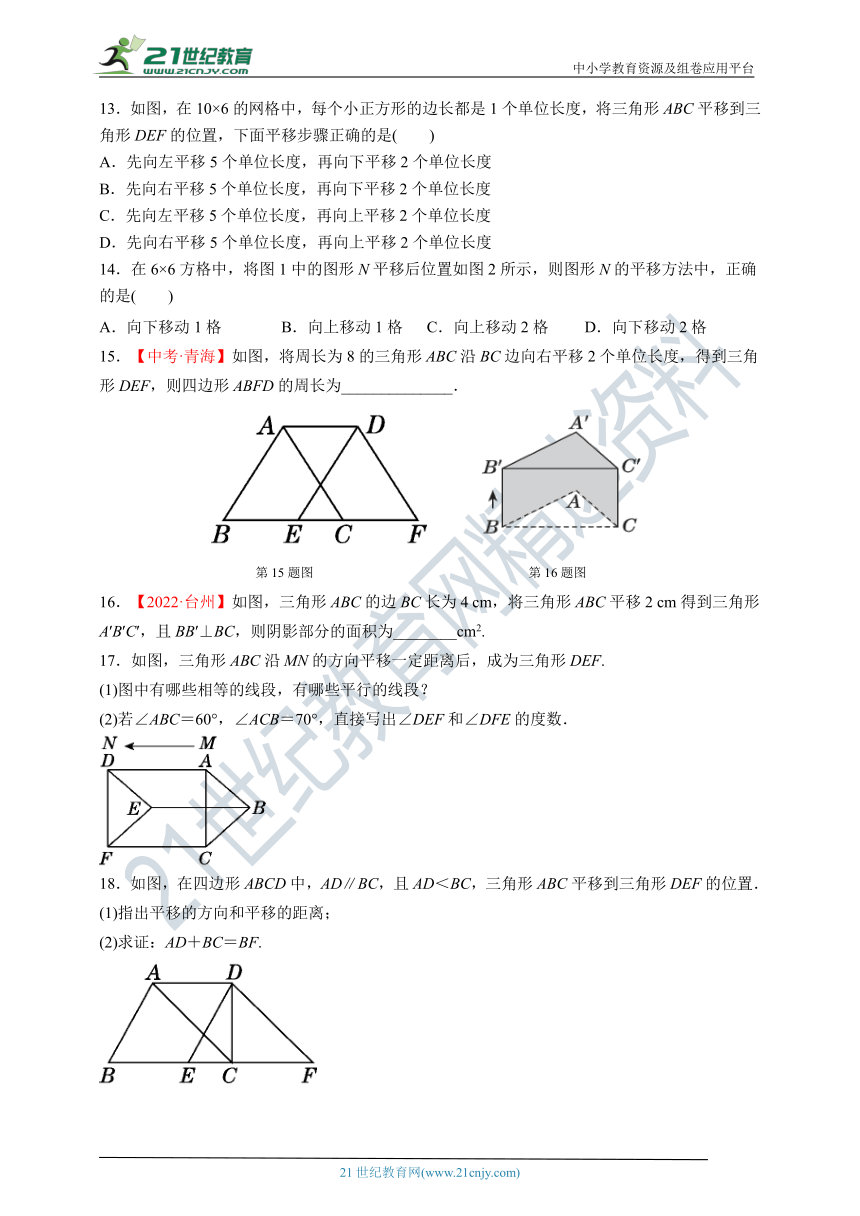
13.如图,在10×6的网格中,每个小正方形的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面平移步骤正确的是( )
A.先向左平移5个单位长度,再向下平移2个单位长度
B.先向右平移5个单位长度,再向下平移2个单位长度
C.先向左平移5个单位长度,再向上平移2个单位长度
D.先向右平移5个单位长度,再向上平移2个单位长度
14.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格 C.向上移动2格 D.向下移动2格
15.【中考·青海】如图,将周长为8的三角形ABC沿BC边向右平移2个单位长度,得到三角形DEF,则四边形ABFD的周长为______________.
第15题图 第16题图
16.【2022·台州】如图,三角形ABC的边BC长为4 cm,将三角形ABC平移2 cm得到三角形A′B′C′,且BB′⊥BC,则阴影部分的面积为________cm2.
17.如图,三角形ABC沿MN的方向平移一定距离后,成为三角形DEF.
(1)图中有哪些相等的线段,有哪些平行的线段?
(2)若∠ABC=60°,∠ACB=70°,直接写出∠DEF和∠DFE的度数.
18.如图,在四边形ABCD中,AD∥BC,且AD<BC,三角形ABC平移到三角形DEF的位置.
(1)指出平移的方向和平移的距离;
(2)求证:AD+BC=BF.
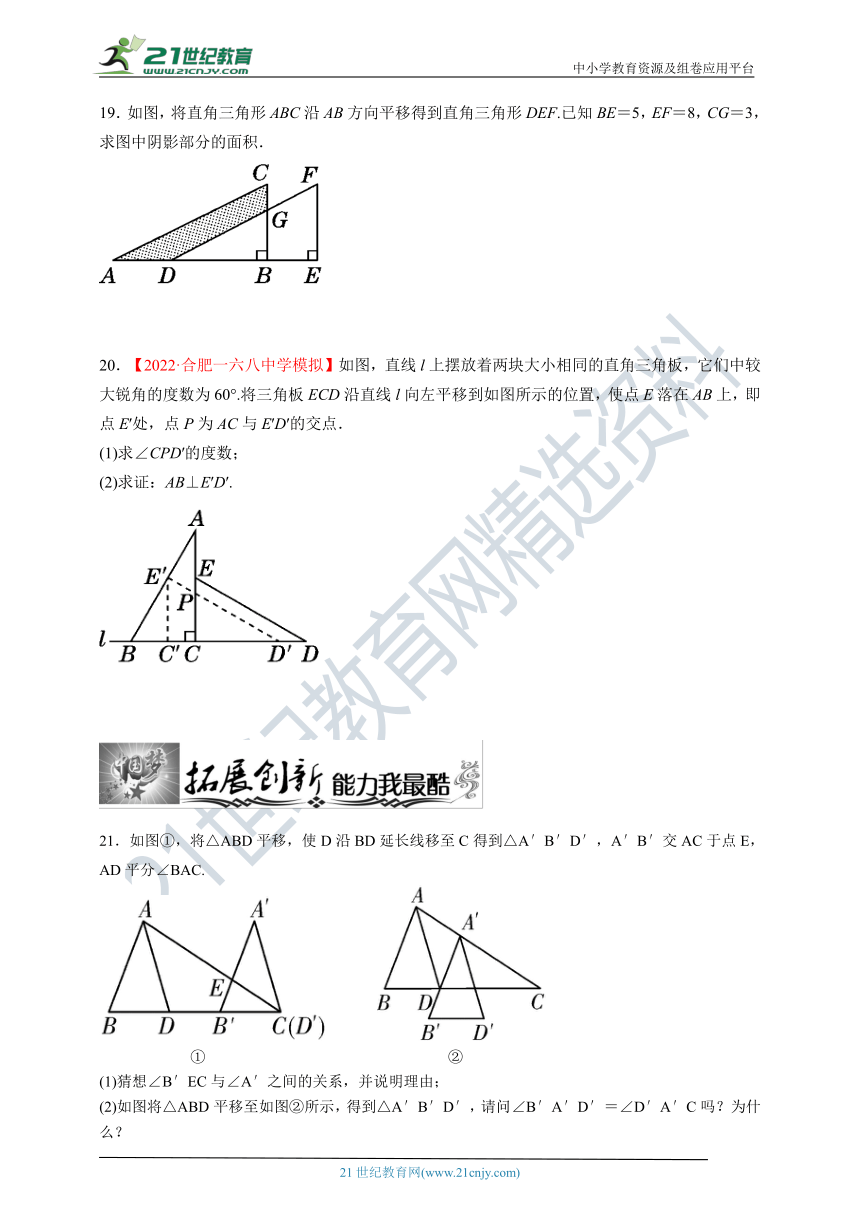
19.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
20.【2022·合肥一六八中学模拟】如图,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将三角板ECD沿直线l向左平移到如图所示的位置,使点E落在AB上,即点E′处,点P为AC与E′D′的交点.
(1)求∠CPD′的度数;
(2)求证:AB⊥E′D′.
21.如图①,将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于点E,AD平分∠BAC.
① ②
(1)猜想∠B′EC与∠A′之间的关系,并说明理由;
(2)如图将△ABD平移至如图②所示,得到△A′B′D′,请问∠B′A′D′=∠D′A′C吗?为什么?
22.如图,图形的操作过程(本题4个图形中的长方形均相同,长为a,宽为b):在图①中,将线段A1A2向右平移1个单位长度到B1B2,得阴影部分A1A2B2B1,在图②中将折线A1A2A3向右平移1个单位长度到B1B2B3,得阴影部分A1A2A3B3B2B1.
(1)在图③中,请你类似设计一个有两个折点的线,同样向右平移1个单位长度,从而得到一个封闭图形;
(2)请你分别写出三个图中除去阴影部分后剩余部分的面积:S1=________,S2=________,S3=______;
(3)拓展运用:图④为一块长方形地,中间有一条小路(小路任何地方水平宽均是1个单位长度),其余部分种草,求草地的面积,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列运动属于平移的是( C )
A.冷水加热过程中小气泡上升成为大汽泡
B.投篮时的篮球运动
C.急刹车时汽车在地面上的滑动
D.随风飘动的树叶在空中的运动
2.将如图所示的图案通过平移后可以得到的图案是( A )
3.下列运动不是平移的是( C )
①传送带上物品的运动;②电梯的升降;③火车在平直的铁轨上运行;④门绕着门框旋转;⑤奥运五环旗图案的形成过程;⑥电风扇的转动.
A.①② B.③④ C.④⑥ D.③⑤
4.如图,三角形ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5,EC=3,那么平移的距离为( A )
A.2 B.3 C.5 D.7
第4题图 第6题图 第7题图
5.(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,这种移动叫做 .
【答案】平移
(2)平移过程:新图形与原图形 、 完全相同;新图形上的每一点都是由它的对应点 后得到的;连接各组对应点的线段 且 .
【答案】形状 大小 平移 平行(或在同一条直线上) 相等
(3)确定一个图形平移后的位置需要三个条件:①图形原来的位置;②平移的 ;③平移的 .
【答案】方向 距离
6.如图所示,将三角形DEF向下平移 格,再向 平移 格得到三角形ABC.
【答案】2 左 4
7.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
【答案】30°
8.如图,三角形ABC是通过平移三角形DEF得到的,已知ED和BA是对应线段,请在图中画出三角形DEF.
解:如图所示,三角形DEF即为所求:
9.以下现象:
①水管里水的流动;②滑雪运动员在笔直的雪道上滑行;
③射出的子弹;④火车在笔直的铁轨上行驶.
其中是平移的是( D )
A.①② B.①③ C.②③ D.②④
10.【2022·广西】2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( D )
11.【2022·湖州】如图,将三角形ABC沿BC方向平移1 cm得到三角形A′B′C′.若B′C=2 cm,则BC′的长是( C )
A.2 cm B.3 cm C.4 cm D.5 cm
第11题图 第13题图 第14题图
12.下列平移作图错误的是( C )
13.如图,在10×6的网格中,每个小正方形的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面平移步骤正确的是( A )
A.先向左平移5个单位长度,再向下平移2个单位长度
B.先向右平移5个单位长度,再向下平移2个单位长度
C.先向左平移5个单位长度,再向上平移2个单位长度
D.先向右平移5个单位长度,再向上平移2个单位长度
14.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( D )
A.向下移动1格 B.向上移动1格 C.向上移动2格 D.向下移动2格
15.【中考·青海】如图,将周长为8的三角形ABC沿BC边向右平移2个单位长度,得到三角形DEF,则四边形ABFD的周长为______________.
【答案】12
第15题图 第16题图
16.【2022·台州】如图,三角形ABC的边BC长为4 cm,将三角形ABC平移2 cm得到三角形A′B′C′,且BB′⊥BC,则阴影部分的面积为________cm2.
【答案】8
17.如图,三角形ABC沿MN的方向平移一定距离后,成为三角形DEF.
(1)图中有哪些相等的线段,有哪些平行的线段?
解:(1)相等的线段有:AB=DE,BC=EF,AC=DF,
AD=BE=CF;平行的线段有:AB∥DE,BC∥EF,
AC∥DF,AD∥BE∥CF.
(2)若∠ABC=60°,∠ACB=70°,直接写出∠DEF和∠DFE的度数.
∠DEF=60°,∠DFE=70°.
18.如图,在四边形ABCD中,AD∥BC,且AD<BC,三角形ABC平移到三角形DEF的位置.
(1)指出平移的方向和平移的距离;
解:平移的方向是点A到点D的方向,
平移的距离是线段AD的长度.
(2)求证:AD+BC=BF.
证明:∵三角形ABC平移到三角形DEF的位置,
∴CF=AD.∵CF+BC=BF,∴AD+BC=BF.
19.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
解:∵直角三角形ABC沿AB方向平移得到直
角三角形DEF,∴三角形ABC的面积与三角形DEF的面积相等,BC=EF,BC∥BF.∴三角形ABC的面积-三角形DBG的面积=三角形DEF的面积-三角形DBG的面积,四边形GBEF为梯形.∴阴影部分的面积与梯形GBEF的面积相等.∵EF=8,CG=3,∴BG=BC-CG=EF-CG=5.又∵BE=5,∴阴影部分的面积为(5+8)×5×=32.5.
20.【2022·合肥一六八中学模拟】如图,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将三角板ECD沿直线l向左平移到如图所示的位置,使点E落在AB上,即点E′处,点P为AC与E′D′的交点.
(1)求∠CPD′的度数;
解:由平移的性质知DE∥D′E′,
∴∠CPD′=∠CED=60°.
(2)求证:AB⊥E′D′.
证明:由平移的性质知CE∥C′E′,
∠CED=∠C′E′D′=60°,
∴∠BE′C′=∠A=30°.
∴∠BE′D′=30°+60°=90°.
∴AB⊥E′D′.
21.如图①,将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于点E,AD平分∠BAC.
① ②
(1)猜想∠B′EC与∠A′之间的关系,并说明理由;
解:∠B′EC=2∠A′,
理由:∵AB∥B′E,AD平分∠BAC.
∴∠B′EC=∠BAC=2∠BAD.
∵∠BAD=∠A′,∴∠B′EC=2∠A′.
(2)如图将△ABD平移至如图②所示,得到△A′B′D′,请问∠B′A′D′=∠D′A′C吗?为什么?
解:A′D′平分∠B′A′C,
理由:∵AB∥A′B′,AD∥A′D′,
∴∠B′A′C=∠BAC,∠DAC=∠D′A′C,
∵AD平分∠BAC,∴∠BAD=∠DAC,
∵∠BAD=∠B′A′D′,∴∠B′A′D′=∠D′A′C.
22.如图,图形的操作过程(本题4个图形中的长方形均相同,长为a,宽为b):在图①中,将线段A1A2向右平移1个单位长度到B1B2,得阴影部分A1A2B2B1,在图②中将折线A1A2A3向右平移1个单位长度到B1B2B3,得阴影部分A1A2A3B3B2B1.
(1)在图③中,请你类似设计一个有两个折点的线,同样向右平移1个单位长度,从而得到一个封闭图形;
解:(1)如图所示.
(2)请你分别写出三个图中除去阴影部分后剩余部分的面积:S1=________,S2=________,S3=______;
【答案】ab-b ab-b ab-b
(3)拓展运用:图④为一块长方形地,中间有一条小路(小路任何地方水平宽均是1个单位长度),其余部分种草,求草地的面积,并说明理由.
草地的面积=ab-b.
理由:把“小路”沿着左右两条边线“剪去”将左侧的草地向右平移1个单位长度,得到一个新长方形,它的长为a-1,宽为b,故其面积是(a-1)b=ab-b.
1.下列运动属于平移的是( )
A.冷水加热过程中小气泡上升成为大汽泡
B.投篮时的篮球运动
C.急刹车时汽车在地面上的滑动
D.随风飘动的树叶在空中的运动
2.将如图所示的图案通过平移后可以得到的图案是( )
3.下列运动不是平移的是( )
①传送带上物品的运动;②电梯的升降;③火车在平直的铁轨上运行;④门绕着门框旋转;⑤奥运五环旗图案的形成过程;⑥电风扇的转动.
A.①② B.③④ C.④⑥ D.③⑤
4.如图,三角形ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5,EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.7
第4题图 第6题图 第7题图
5.(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,这种移动叫做 .
(2)平移过程:新图形与原图形 、 完全相同;新图形上的每一点都是由它的对应点 后得到的;连接各组对应点的线段 且 .
(3)确定一个图形平移后的位置需要三个条件:①图形原来的位置;②平移的 ;③平移的 .
6.如图所示,将三角形DEF向下平移 格,再向 平移 格得到三角形ABC.
7.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
8.如图,三角形ABC是通过平移三角形DEF得到的,已知ED和BA是对应线段,请在图中画出三角形DEF.
9.以下现象:
①水管里水的流动;②滑雪运动员在笔直的雪道上滑行;
③射出的子弹;④火车在笔直的铁轨上行驶.
其中是平移的是( )
A.①② B.①③ C.②③ D.②④
10.【2022·广西】2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( )
11.【2022·湖州】如图,将三角形ABC沿BC方向平移1 cm得到三角形A′B′C′.若B′C=2 cm,则BC′的长是( )
A.2 cm B.3 cm C.4 cm D.5 cm
第11题图 第13题图 第14题图
12.下列平移作图错误的是( )
13.如图,在10×6的网格中,每个小正方形的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面平移步骤正确的是( )
A.先向左平移5个单位长度,再向下平移2个单位长度
B.先向右平移5个单位长度,再向下平移2个单位长度
C.先向左平移5个单位长度,再向上平移2个单位长度
D.先向右平移5个单位长度,再向上平移2个单位长度
14.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格 C.向上移动2格 D.向下移动2格
15.【中考·青海】如图,将周长为8的三角形ABC沿BC边向右平移2个单位长度,得到三角形DEF,则四边形ABFD的周长为______________.
第15题图 第16题图
16.【2022·台州】如图,三角形ABC的边BC长为4 cm,将三角形ABC平移2 cm得到三角形A′B′C′,且BB′⊥BC,则阴影部分的面积为________cm2.
17.如图,三角形ABC沿MN的方向平移一定距离后,成为三角形DEF.
(1)图中有哪些相等的线段,有哪些平行的线段?
(2)若∠ABC=60°,∠ACB=70°,直接写出∠DEF和∠DFE的度数.
18.如图,在四边形ABCD中,AD∥BC,且AD<BC,三角形ABC平移到三角形DEF的位置.
(1)指出平移的方向和平移的距离;
(2)求证:AD+BC=BF.
19.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
20.【2022·合肥一六八中学模拟】如图,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将三角板ECD沿直线l向左平移到如图所示的位置,使点E落在AB上,即点E′处,点P为AC与E′D′的交点.
(1)求∠CPD′的度数;
(2)求证:AB⊥E′D′.
21.如图①,将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于点E,AD平分∠BAC.
① ②
(1)猜想∠B′EC与∠A′之间的关系,并说明理由;
(2)如图将△ABD平移至如图②所示,得到△A′B′D′,请问∠B′A′D′=∠D′A′C吗?为什么?
22.如图,图形的操作过程(本题4个图形中的长方形均相同,长为a,宽为b):在图①中,将线段A1A2向右平移1个单位长度到B1B2,得阴影部分A1A2B2B1,在图②中将折线A1A2A3向右平移1个单位长度到B1B2B3,得阴影部分A1A2A3B3B2B1.
(1)在图③中,请你类似设计一个有两个折点的线,同样向右平移1个单位长度,从而得到一个封闭图形;
(2)请你分别写出三个图中除去阴影部分后剩余部分的面积:S1=________,S2=________,S3=______;
(3)拓展运用:图④为一块长方形地,中间有一条小路(小路任何地方水平宽均是1个单位长度),其余部分种草,求草地的面积,并说明理由.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
1.下列运动属于平移的是( C )
A.冷水加热过程中小气泡上升成为大汽泡
B.投篮时的篮球运动
C.急刹车时汽车在地面上的滑动
D.随风飘动的树叶在空中的运动
2.将如图所示的图案通过平移后可以得到的图案是( A )
3.下列运动不是平移的是( C )
①传送带上物品的运动;②电梯的升降;③火车在平直的铁轨上运行;④门绕着门框旋转;⑤奥运五环旗图案的形成过程;⑥电风扇的转动.
A.①② B.③④ C.④⑥ D.③⑤
4.如图,三角形ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5,EC=3,那么平移的距离为( A )
A.2 B.3 C.5 D.7
第4题图 第6题图 第7题图
5.(1)把一个图形整体沿某一直线方向移动,会得到一个新的图形,这种移动叫做 .
【答案】平移
(2)平移过程:新图形与原图形 、 完全相同;新图形上的每一点都是由它的对应点 后得到的;连接各组对应点的线段 且 .
【答案】形状 大小 平移 平行(或在同一条直线上) 相等
(3)确定一个图形平移后的位置需要三个条件:①图形原来的位置;②平移的 ;③平移的 .
【答案】方向 距离
6.如图所示,将三角形DEF向下平移 格,再向 平移 格得到三角形ABC.
【答案】2 左 4
7.如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .
【答案】30°
8.如图,三角形ABC是通过平移三角形DEF得到的,已知ED和BA是对应线段,请在图中画出三角形DEF.
解:如图所示,三角形DEF即为所求:
9.以下现象:
①水管里水的流动;②滑雪运动员在笔直的雪道上滑行;
③射出的子弹;④火车在笔直的铁轨上行驶.
其中是平移的是( D )
A.①② B.①③ C.②③ D.②④
10.【2022·广西】2022北京冬残奥会的会徽是以汉字“飞”为灵感来设计的,展现了运动员不断飞跃,超越自我,奋力拼搏,激励世界的冬残奥精神.下列的四个图中,能由如图所示的会徽经过平移得到的是( D )
11.【2022·湖州】如图,将三角形ABC沿BC方向平移1 cm得到三角形A′B′C′.若B′C=2 cm,则BC′的长是( C )
A.2 cm B.3 cm C.4 cm D.5 cm
第11题图 第13题图 第14题图
12.下列平移作图错误的是( C )
13.如图,在10×6的网格中,每个小正方形的边长都是1个单位长度,将三角形ABC平移到三角形DEF的位置,下面平移步骤正确的是( A )
A.先向左平移5个单位长度,再向下平移2个单位长度
B.先向右平移5个单位长度,再向下平移2个单位长度
C.先向左平移5个单位长度,再向上平移2个单位长度
D.先向右平移5个单位长度,再向上平移2个单位长度
14.在6×6方格中,将图1中的图形N平移后位置如图2所示,则图形N的平移方法中,正确的是( D )
A.向下移动1格 B.向上移动1格 C.向上移动2格 D.向下移动2格
15.【中考·青海】如图,将周长为8的三角形ABC沿BC边向右平移2个单位长度,得到三角形DEF,则四边形ABFD的周长为______________.
【答案】12
第15题图 第16题图
16.【2022·台州】如图,三角形ABC的边BC长为4 cm,将三角形ABC平移2 cm得到三角形A′B′C′,且BB′⊥BC,则阴影部分的面积为________cm2.
【答案】8
17.如图,三角形ABC沿MN的方向平移一定距离后,成为三角形DEF.
(1)图中有哪些相等的线段,有哪些平行的线段?
解:(1)相等的线段有:AB=DE,BC=EF,AC=DF,
AD=BE=CF;平行的线段有:AB∥DE,BC∥EF,
AC∥DF,AD∥BE∥CF.
(2)若∠ABC=60°,∠ACB=70°,直接写出∠DEF和∠DFE的度数.
∠DEF=60°,∠DFE=70°.
18.如图,在四边形ABCD中,AD∥BC,且AD<BC,三角形ABC平移到三角形DEF的位置.
(1)指出平移的方向和平移的距离;
解:平移的方向是点A到点D的方向,
平移的距离是线段AD的长度.
(2)求证:AD+BC=BF.
证明:∵三角形ABC平移到三角形DEF的位置,
∴CF=AD.∵CF+BC=BF,∴AD+BC=BF.
19.如图,将直角三角形ABC沿AB方向平移得到直角三角形DEF.已知BE=5,EF=8,CG=3,求图中阴影部分的面积.
解:∵直角三角形ABC沿AB方向平移得到直
角三角形DEF,∴三角形ABC的面积与三角形DEF的面积相等,BC=EF,BC∥BF.∴三角形ABC的面积-三角形DBG的面积=三角形DEF的面积-三角形DBG的面积,四边形GBEF为梯形.∴阴影部分的面积与梯形GBEF的面积相等.∵EF=8,CG=3,∴BG=BC-CG=EF-CG=5.又∵BE=5,∴阴影部分的面积为(5+8)×5×=32.5.
20.【2022·合肥一六八中学模拟】如图,直线l上摆放着两块大小相同的直角三角板,它们中较大锐角的度数为60°.将三角板ECD沿直线l向左平移到如图所示的位置,使点E落在AB上,即点E′处,点P为AC与E′D′的交点.
(1)求∠CPD′的度数;
解:由平移的性质知DE∥D′E′,
∴∠CPD′=∠CED=60°.
(2)求证:AB⊥E′D′.
证明:由平移的性质知CE∥C′E′,
∠CED=∠C′E′D′=60°,
∴∠BE′C′=∠A=30°.
∴∠BE′D′=30°+60°=90°.
∴AB⊥E′D′.
21.如图①,将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于点E,AD平分∠BAC.
① ②
(1)猜想∠B′EC与∠A′之间的关系,并说明理由;
解:∠B′EC=2∠A′,
理由:∵AB∥B′E,AD平分∠BAC.
∴∠B′EC=∠BAC=2∠BAD.
∵∠BAD=∠A′,∴∠B′EC=2∠A′.
(2)如图将△ABD平移至如图②所示,得到△A′B′D′,请问∠B′A′D′=∠D′A′C吗?为什么?
解:A′D′平分∠B′A′C,
理由:∵AB∥A′B′,AD∥A′D′,
∴∠B′A′C=∠BAC,∠DAC=∠D′A′C,
∵AD平分∠BAC,∴∠BAD=∠DAC,
∵∠BAD=∠B′A′D′,∴∠B′A′D′=∠D′A′C.
22.如图,图形的操作过程(本题4个图形中的长方形均相同,长为a,宽为b):在图①中,将线段A1A2向右平移1个单位长度到B1B2,得阴影部分A1A2B2B1,在图②中将折线A1A2A3向右平移1个单位长度到B1B2B3,得阴影部分A1A2A3B3B2B1.
(1)在图③中,请你类似设计一个有两个折点的线,同样向右平移1个单位长度,从而得到一个封闭图形;
解:(1)如图所示.
(2)请你分别写出三个图中除去阴影部分后剩余部分的面积:S1=________,S2=________,S3=______;
【答案】ab-b ab-b ab-b
(3)拓展运用:图④为一块长方形地,中间有一条小路(小路任何地方水平宽均是1个单位长度),其余部分种草,求草地的面积,并说明理由.
草地的面积=ab-b.
理由:把“小路”沿着左右两条边线“剪去”将左侧的草地向右平移1个单位长度,得到一个新长方形,它的长为a-1,宽为b,故其面积是(a-1)b=ab-b.
