7.3 频数和频率 课件(共25张PPT)
文档属性
| 名称 | 7.3 频数和频率 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
7.3频数和频率
第7章 数据的收集、整理、描述
教师
xxx
苏科版 八年级下册
频数和频率
01
CONTANTS
目 录
频数和频率
01
在课堂上,针对某一问题,老师提问全体同学,学生们纷纷举手回答。
老师通过学生举手的情况,就能看出本班学生大约能够解决这类问题的人数
情景引入
问题呈现
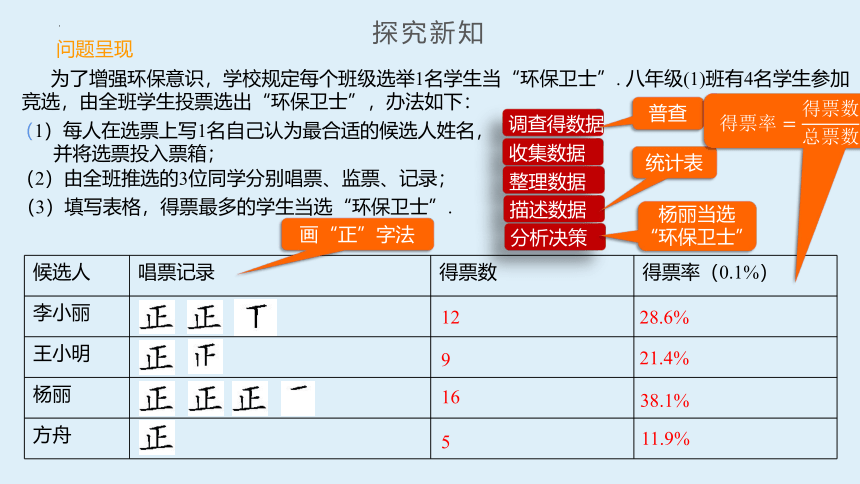
为了增强环保意识,学校规定每个班级选举1名学生当“环保卫士”. 八年级(1)班有4名学生参加竞选,由全班学生投票选出“环保卫士”,办法如下:
(3)填写表格,得票最多的学生当选“环保卫士”.
(1)每人在选票上写1名自己认为最合适的候选人姓名,
并将选票投入票箱;
(2)由全班推选的3位同学分别唱票、监票、记录;
候选人 唱票记录 得票数 得票率(0.1%)
李小丽
王小明
杨丽
方舟
调查得数据
普查
收集数据
整理数据
描述数据
分析决策
统计表
画“正”字法
杨丽当选
“环保卫士”
12
9
16
5
28.6%
21.4%
38.1%
11.9%
探究新知
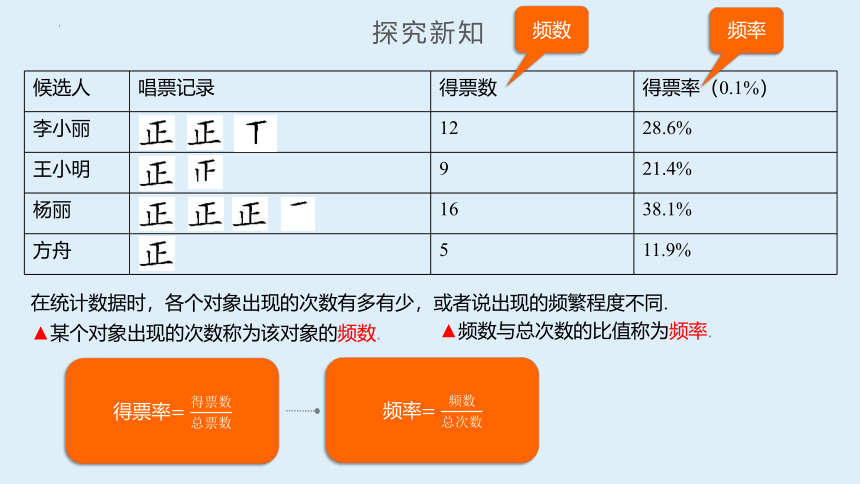
候选人 唱票记录 得票数 得票率(0.1%)
李小丽 12 28.6%
王小明 9 21.4%
杨丽 16 38.1%
方舟 5 11.9%
频数
频率
在统计数据时,各个对象出现的次数有多有少,或者说出现的频繁程度不同.
▲某个对象出现的次数称为该对象的频数.
▲频数与总次数的比值称为频率.
得票率
频率
探究新知
候选人 频数 频率(0.1%)
李小丽 12 28.6%
王小明 9 21.4%
杨 丽 16 38.1%
方 舟 5 11.9%
合 计
42
1
▲各个对象出现的频数之和等于总次数.
12+9+16+5=42
28.6%+21.4%+38.1%+11.9%=1
▲各个对象出现的频率之和等于1.
+
+
+
=1
某个对象出现的次数
频率
八(1)班20个女生的身高如下(单位:cm):153,156,152,158,156,160,163,145,152,153,162,153,165,150,157,153,158,157,158,158.请在表格中填出身高在以下各范围内的频数和频率.
身高 140 ~ 149.5 149.5 ~ 159.5 159.5 ~ 170
划记
频数
频率
1
4
15
0.75
0.2
0.05
“身高140 ~ 149.9”频率=0.05
“身高149.5~159.9”频率=0.75
“身高159.5 ~ 170”频率=0.2
“各个对象出现的次数之和等于总次数”、“各个对象出现的频率之和等于1”.
某个对象出现的次数
频率
探究新知
八(1)班男生身高统计数据如下表所示:(单位:cm)但校医在数据录入时不慎将墨水弄脏了表格,导致部分数据未知,你能用所学知识帮助校医找回数据吗?
身高(cm) 160 ~ 169.5 169.5 ~ 179.5 179.5 ~ 190
频数
频率
6
0.25
15
▲频数、频率和总次数之间的关系:
频率
频数总次数×频率
24;
3;
0.125;
0.625.
3
0.125
0.625
“各个对象出现的次数之和等于总次数”、“各个对象出现的频率之和等于1”.
探究新知
某中学计划对八年级的480名学生按“学科”、“文体”、“手工”三个项目安排课外兴趣小组,小明从每班随机抽取5名学生进行问卷调查,并将统计结果制成如下所示的统计表和统计图:(1)请将统计表、统计图补充完整;(2)请以小明的统计结果来估计该校八年级480名学生参加各个项目的人数。
兴趣小组 频数 频率
学科 50%
文体
手工 15
合计
10
50
1
30%
解:(2)学科:480×50%=240(人)
手工:480×30%=144(人)
文体:480×20%=96(人)
答:该校八年级480名学生参加“学科”的约有240人,参加“文体”的约有96人,参加“手工”的约有144人.
频率
频数总次数×频率
20%
25
“各个对象出现的次数之和等于总次数”、“各个对象出现的频率之和等于1”.
国家环保总局公布的47个重点城市的空气质量如下:
城市 郑州 武汉 长沙 广州 深圳 珠海 汕头 湛江 南宁 桂林 北海
污染指数 85 99 107 119 94 78 67 51 111 52 62
海口 成都 重庆 贵阳 昆明 拉萨 西安 兰州 西宁 银川 乌鲁木齐 北京
49 114 174 96 74 76 128 128 97 65 205 64
天津 石家庄 秦皇岛 太原 呼和浩特 沈阳 大连 长春 哈尔滨 上海 南京
81 98 73 125 124 138 68 90 98 86 74
苏州 南通 连云港 杭州 宁波 温州 合肥 福州 厦门 南昌 济南 青岛 烟台
89 79 71 92 80 82 81 79 66 101 93 73 53
典型例题
国家环保总局规定:
空气污染指数 1~50为Ⅰ级,51~100为Ⅱ级,
101~200为Ⅲ级,201~300为Ⅳ级.
请按城市空气质量级别填表,并用合适的统计图表示.
空气污染指数 Ⅰ级 Ⅱ级 Ⅲ级 Ⅳ级
划记
频数
频率 (精确到0.001)
注意:将一组数据分层若干组,各组的频数是指落在该组中的数据的个数;各组的频率是指该组的频数与数据总数的比值.
典型例题
空气污染指数 Ⅰ级 Ⅱ级 Ⅲ级 Ⅳ级
频数 1 34 11 1
频率 0.021 0.724 0.234 0.021
解:图表如下.
典型例题
1.将数据83,85,87,89,84,85,86,88,87,90分组,86.5~88.5这组的频数是( )
A.1 B.2
C.3 D.4
C
课堂练习
2.已知60个数分别落在5个组内,第一、二、三 、四、五组数据的个数分别是12,8,x,20,5,则第三组的频数为________.
15
课堂练习
3.一次数学测试后,某班40名学生的成绩被分为优、良、中、差,其中优、良、中的频数分别为16、12、8,则差的频率是( )
A.0.1 B.0.2
C.0.3 D.0.4
A
课堂练习
4.下列说法错误的是( )
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件A试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
A
课堂练习
5.学校为了了解八年级学生参加课外活动兴趣小组的情况,随机抽查了40名学生(每人只能参加一个兴趣小组),将调查结果列出如下所示的统计表,则八年级学生参加书法兴趣小组的频率是( )
组别 书法 绘画 舞蹈 其他
人数 8 12 11 9
A.0.1 B.0.15 C.0.2 D.0.3
C
课堂练习
6.为了了解某中学八年级男生的身体发育情况,从该中学八年级男生中随机抽取40名男生的身高进行了测量,已知身高(单位:cm)在1.60~1.65这一小组的频数为6,则身高在1.60~1.65这一小组的频率是________.
0.15
课堂练习
7.如图是某景点6月份内1~10日每天的最高温度折线统计图,由图上信息可知该景点这10天中,气温26 ℃出现的频率是________.
0.3
课堂练习
8.某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
学生孝敬父母情况统计表
选项 频数 频率
A m 0.15
B 60 p
C n 0.4
D 48 0.2
课堂练习
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
解:这次被调查的学生有48÷0.2=240(人).
课堂练习
(3)该校有1 600名学生,估计该校全体学生中选择B选项的有多少人.
解:估计该校全体学生中选择B选项的有
1 600×0.25=400(人).
课堂练习
频率=
频数
总次数
频数=
频数、频率和总次数之间的关系:
总次数=
频率
频数
总次数 × 频率
频数之和等于总次数,频率之和等于1
课堂小结
感谢观看
7.3频数和频率
第7章 数据的收集、整理、描述
教师
xxx
苏科版 八年级下册
频数和频率
01
CONTANTS
目 录
频数和频率
01
在课堂上,针对某一问题,老师提问全体同学,学生们纷纷举手回答。
老师通过学生举手的情况,就能看出本班学生大约能够解决这类问题的人数
情景引入
问题呈现
为了增强环保意识,学校规定每个班级选举1名学生当“环保卫士”. 八年级(1)班有4名学生参加竞选,由全班学生投票选出“环保卫士”,办法如下:
(3)填写表格,得票最多的学生当选“环保卫士”.
(1)每人在选票上写1名自己认为最合适的候选人姓名,
并将选票投入票箱;
(2)由全班推选的3位同学分别唱票、监票、记录;
候选人 唱票记录 得票数 得票率(0.1%)
李小丽
王小明
杨丽
方舟
调查得数据
普查
收集数据
整理数据
描述数据
分析决策
统计表
画“正”字法
杨丽当选
“环保卫士”
12
9
16
5
28.6%
21.4%
38.1%
11.9%
探究新知
候选人 唱票记录 得票数 得票率(0.1%)
李小丽 12 28.6%
王小明 9 21.4%
杨丽 16 38.1%
方舟 5 11.9%
频数
频率
在统计数据时,各个对象出现的次数有多有少,或者说出现的频繁程度不同.
▲某个对象出现的次数称为该对象的频数.
▲频数与总次数的比值称为频率.
得票率
频率
探究新知
候选人 频数 频率(0.1%)
李小丽 12 28.6%
王小明 9 21.4%
杨 丽 16 38.1%
方 舟 5 11.9%
合 计
42
1
▲各个对象出现的频数之和等于总次数.
12+9+16+5=42
28.6%+21.4%+38.1%+11.9%=1
▲各个对象出现的频率之和等于1.
+
+
+
=1
某个对象出现的次数
频率
八(1)班20个女生的身高如下(单位:cm):153,156,152,158,156,160,163,145,152,153,162,153,165,150,157,153,158,157,158,158.请在表格中填出身高在以下各范围内的频数和频率.
身高 140 ~ 149.5 149.5 ~ 159.5 159.5 ~ 170
划记
频数
频率
1
4
15
0.75
0.2
0.05
“身高140 ~ 149.9”频率=0.05
“身高149.5~159.9”频率=0.75
“身高159.5 ~ 170”频率=0.2
“各个对象出现的次数之和等于总次数”、“各个对象出现的频率之和等于1”.
某个对象出现的次数
频率
探究新知
八(1)班男生身高统计数据如下表所示:(单位:cm)但校医在数据录入时不慎将墨水弄脏了表格,导致部分数据未知,你能用所学知识帮助校医找回数据吗?
身高(cm) 160 ~ 169.5 169.5 ~ 179.5 179.5 ~ 190
频数
频率
6
0.25
15
▲频数、频率和总次数之间的关系:
频率
频数总次数×频率
24;
3;
0.125;
0.625.
3
0.125
0.625
“各个对象出现的次数之和等于总次数”、“各个对象出现的频率之和等于1”.
探究新知
某中学计划对八年级的480名学生按“学科”、“文体”、“手工”三个项目安排课外兴趣小组,小明从每班随机抽取5名学生进行问卷调查,并将统计结果制成如下所示的统计表和统计图:(1)请将统计表、统计图补充完整;(2)请以小明的统计结果来估计该校八年级480名学生参加各个项目的人数。
兴趣小组 频数 频率
学科 50%
文体
手工 15
合计
10
50
1
30%
解:(2)学科:480×50%=240(人)
手工:480×30%=144(人)
文体:480×20%=96(人)
答:该校八年级480名学生参加“学科”的约有240人,参加“文体”的约有96人,参加“手工”的约有144人.
频率
频数总次数×频率
20%
25
“各个对象出现的次数之和等于总次数”、“各个对象出现的频率之和等于1”.
国家环保总局公布的47个重点城市的空气质量如下:
城市 郑州 武汉 长沙 广州 深圳 珠海 汕头 湛江 南宁 桂林 北海
污染指数 85 99 107 119 94 78 67 51 111 52 62
海口 成都 重庆 贵阳 昆明 拉萨 西安 兰州 西宁 银川 乌鲁木齐 北京
49 114 174 96 74 76 128 128 97 65 205 64
天津 石家庄 秦皇岛 太原 呼和浩特 沈阳 大连 长春 哈尔滨 上海 南京
81 98 73 125 124 138 68 90 98 86 74
苏州 南通 连云港 杭州 宁波 温州 合肥 福州 厦门 南昌 济南 青岛 烟台
89 79 71 92 80 82 81 79 66 101 93 73 53
典型例题
国家环保总局规定:
空气污染指数 1~50为Ⅰ级,51~100为Ⅱ级,
101~200为Ⅲ级,201~300为Ⅳ级.
请按城市空气质量级别填表,并用合适的统计图表示.
空气污染指数 Ⅰ级 Ⅱ级 Ⅲ级 Ⅳ级
划记
频数
频率 (精确到0.001)
注意:将一组数据分层若干组,各组的频数是指落在该组中的数据的个数;各组的频率是指该组的频数与数据总数的比值.
典型例题
空气污染指数 Ⅰ级 Ⅱ级 Ⅲ级 Ⅳ级
频数 1 34 11 1
频率 0.021 0.724 0.234 0.021
解:图表如下.
典型例题
1.将数据83,85,87,89,84,85,86,88,87,90分组,86.5~88.5这组的频数是( )
A.1 B.2
C.3 D.4
C
课堂练习
2.已知60个数分别落在5个组内,第一、二、三 、四、五组数据的个数分别是12,8,x,20,5,则第三组的频数为________.
15
课堂练习
3.一次数学测试后,某班40名学生的成绩被分为优、良、中、差,其中优、良、中的频数分别为16、12、8,则差的频率是( )
A.0.1 B.0.2
C.0.3 D.0.4
A
课堂练习
4.下列说法错误的是( )
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件A试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
A
课堂练习
5.学校为了了解八年级学生参加课外活动兴趣小组的情况,随机抽查了40名学生(每人只能参加一个兴趣小组),将调查结果列出如下所示的统计表,则八年级学生参加书法兴趣小组的频率是( )
组别 书法 绘画 舞蹈 其他
人数 8 12 11 9
A.0.1 B.0.15 C.0.2 D.0.3
C
课堂练习
6.为了了解某中学八年级男生的身体发育情况,从该中学八年级男生中随机抽取40名男生的身高进行了测量,已知身高(单位:cm)在1.60~1.65这一小组的频数为6,则身高在1.60~1.65这一小组的频率是________.
0.15
课堂练习
7.如图是某景点6月份内1~10日每天的最高温度折线统计图,由图上信息可知该景点这10天中,气温26 ℃出现的频率是________.
0.3
课堂练习
8.某校为了了解学生孝敬父母的情况(选项:A.为父母洗一次脚;B.帮父母做一次家务;C.给父母买一件礼物;D.其他),在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
学生孝敬父母情况统计表
选项 频数 频率
A m 0.15
B 60 p
C n 0.4
D 48 0.2
课堂练习
根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
解:这次被调查的学生有48÷0.2=240(人).
课堂练习
(3)该校有1 600名学生,估计该校全体学生中选择B选项的有多少人.
解:估计该校全体学生中选择B选项的有
1 600×0.25=400(人).
课堂练习
频率=
频数
总次数
频数=
频数、频率和总次数之间的关系:
总次数=
频率
频数
总次数 × 频率
频数之和等于总次数,频率之和等于1
课堂小结
感谢观看
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
