16.3 二次根式的加减(第1课时) 课件(共32张PPT)
文档属性
| 名称 | 16.3 二次根式的加减(第1课时) 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
16.3二次根式的加减(第1课时)
第16章 二次根式
教师
xxx
人教版 八年级下册
二次根式的加减法则
二次根式加减的应用
二次根式乘除与加减的对比
01
03
02
CONTANTS
目 录
二次根式的加减法则
01
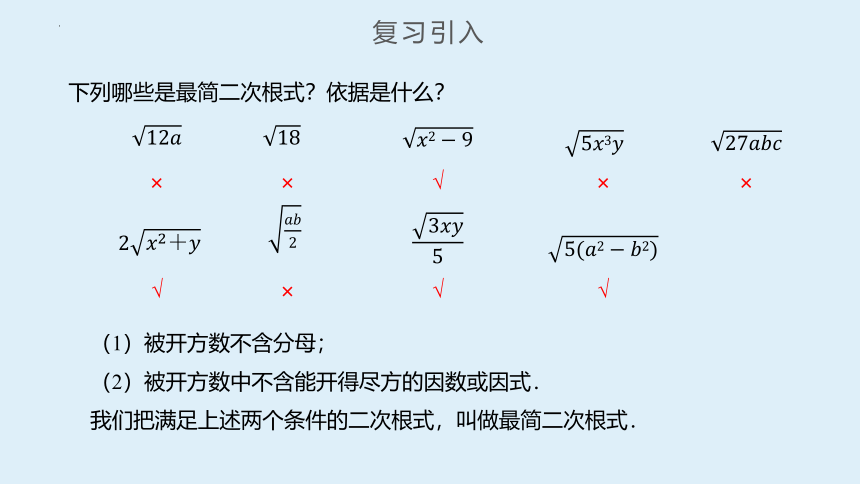
下列哪些是最简二次根式?依据是什么?
√
×
×
×
×
×
√
√
√
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
复习引入
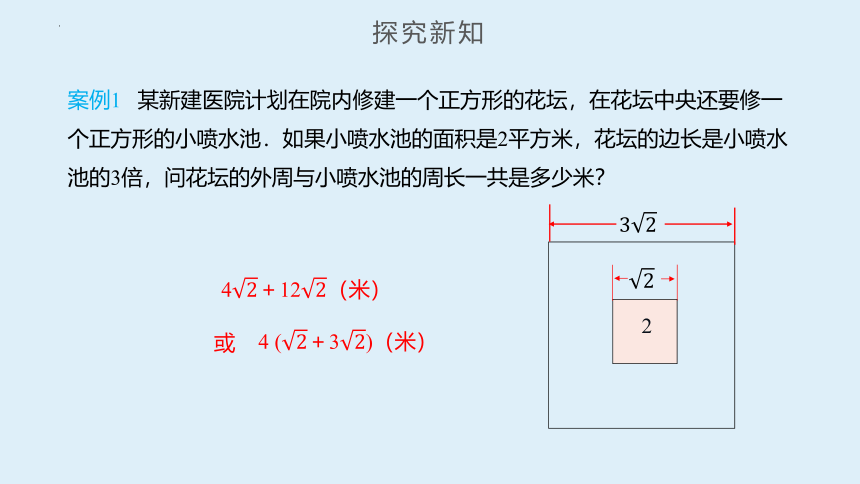
案例1 某新建医院计划在院内修建一个正方形的花坛,在花坛中央还要修一个正方形的小喷水池.如果小喷水池的面积是2平方米,花坛的边长是小喷水池的3倍,问花坛的外周与小喷水池的周长一共是多少米?
2
4+12(米)
4 (+3)(米)
或
探究新知
8
10
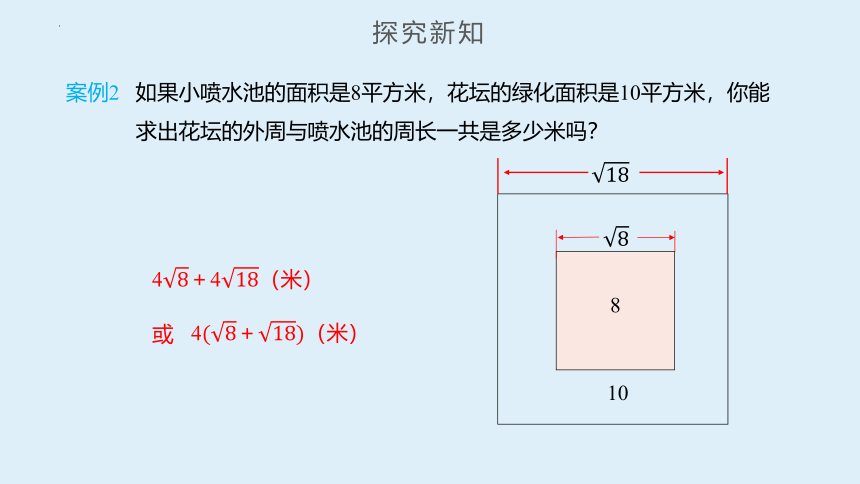
案例2 如果小喷水池的面积是8平方米,花坛的绿化面积是10平方米,你能
求出花坛的外周与喷水池的周长一共是多少米吗?
4+4(米)
4+(米)
或
探究新知
案例1:
4+12
4 (+3)
或
案例2:
4+4
4 +)
或
2
3
二次根式的加减是如何计算的?
探究新知
计算:
(1)3x2+2x2=______; (2)x2+2x2+4y=________.
5x2
3x2+4y
4+1
4+ 4
类比合并同类项的方法,下列二次根式能合并吗?
探究新知
二次根式加减运算的基本方法
结论1: 如果几个二次根式的被开方数相同, 那么可直接根据分配律进行加减运算.
…… (分配律)
4+1
=(4+12)
=16
探究新知
结论2:如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算.
……(化为最简二次根式)
……(分配律)
4+ 4
=8+1
=(8+12)
=2
二次根式加减运算的基本方法
探究新知
注意:被开方数不同的二次根式(如与)不能合并.
判断:下列计算是否正确?为什么?
(1)+ =; (2)2+ =2;
(3) =+ =2+3=5.
二次根式的加减法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
×
×
×
探究新知
同类二次根式(选学)
几个二次根式化成_______________以后,如果__________相同,这几个二次根式就叫做同类二次根式 .
最简二次根式
被开方数
判断几个二次根式是同类二次根式的方法:
一是化每个二次根式为最简二次根式;
二是看化简后的二次根式中被开方数是否相同.
1.下列各式中,与 同类二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则m=_____.
1
3.下列二次根式,不能与 合并的是________(填
序号).
②⑤
针对练习
例1 计算:
最简二次根式
被开方数相同的二次根式
合并
一化,二找,三合并
典型例题
不能合并
例2 计算:
典型例题
二次根式加减运算的一般步骤
1.化:将每个二次根式都化成最简二次根式;
2.找:找出被开方数相同的二次根式;
3.合:将被开方数相同的二次根式合并成一项.
探究新知
计算后根号外的因数是分数的要写成假分数形式,不能写成带分数形式.
计算:
+-(-).
针对练习
思考:(2)中被开方数有小数,该怎样计算?
将被开方数中的小数化为分数,再进行计算.
二次根式的乘除与加减的对比
02
运算 二次根式的乘除 二次根式的加减
系数
被开方数
化简
二次根式的乘除与二次根式的加减的对比
系数相乘除
系数相加减
被开方数相乘除
被开方数不变
结果化为最简
二次根式
先化为最简二次根式,再合并被开方数相同的二次根式
探究新知
二次根式加减的应用
03
例3 已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成
三角形,求出其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:∵ 即a<c<b,
又∵ ∴a+c>b,
∴能构成三角形,周长为
分析:(1)若几个非负数的和为零,则这几个非负数必须为零;(2)根据三角形的三边关系来判断.
典型例题
例4 有一个等腰三角形的两边长分别为
,求其周长.
解: 当腰长为 时,
∵
∴此时能构成三角形,周长为
当腰长为 时,
∵
∴此时能构成三角形,周长为
典型例题
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
法则
步骤
同类二次根式(选学)
二次根式的加减
一般地,二次根式加减时,
可以先将二次根式化简成最简二次根式,
再将被开方数相同的二次根式进行合并.
一化,二找,三合并.
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
课堂小结
感谢观看
16.3二次根式的加减(第1课时)
第16章 二次根式
教师
xxx
人教版 八年级下册
二次根式的加减法则
二次根式加减的应用
二次根式乘除与加减的对比
01
03
02
CONTANTS
目 录
二次根式的加减法则
01
下列哪些是最简二次根式?依据是什么?
√
×
×
×
×
×
√
√
√
我们把满足上述两个条件的二次根式,叫做最简二次根式.
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
复习引入
案例1 某新建医院计划在院内修建一个正方形的花坛,在花坛中央还要修一个正方形的小喷水池.如果小喷水池的面积是2平方米,花坛的边长是小喷水池的3倍,问花坛的外周与小喷水池的周长一共是多少米?
2
4+12(米)
4 (+3)(米)
或
探究新知
8
10
案例2 如果小喷水池的面积是8平方米,花坛的绿化面积是10平方米,你能
求出花坛的外周与喷水池的周长一共是多少米吗?
4+4(米)
4+(米)
或
探究新知
案例1:
4+12
4 (+3)
或
案例2:
4+4
4 +)
或
2
3
二次根式的加减是如何计算的?
探究新知
计算:
(1)3x2+2x2=______; (2)x2+2x2+4y=________.
5x2
3x2+4y
4+1
4+ 4
类比合并同类项的方法,下列二次根式能合并吗?
探究新知
二次根式加减运算的基本方法
结论1: 如果几个二次根式的被开方数相同, 那么可直接根据分配律进行加减运算.
…… (分配律)
4+1
=(4+12)
=16
探究新知
结论2:如果所给的二次根式不是最简二次根式,应该先化简,再考虑进行加减运算.
……(化为最简二次根式)
……(分配律)
4+ 4
=8+1
=(8+12)
=2
二次根式加减运算的基本方法
探究新知
注意:被开方数不同的二次根式(如与)不能合并.
判断:下列计算是否正确?为什么?
(1)+ =; (2)2+ =2;
(3) =+ =2+3=5.
二次根式的加减法则
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
×
×
×
探究新知
同类二次根式(选学)
几个二次根式化成_______________以后,如果__________相同,这几个二次根式就叫做同类二次根式 .
最简二次根式
被开方数
判断几个二次根式是同类二次根式的方法:
一是化每个二次根式为最简二次根式;
二是看化简后的二次根式中被开方数是否相同.
1.下列各式中,与 同类二次根式的是( )
A. B. C. D.
D
2. 与最简二次根式 能合并,则m=_____.
1
3.下列二次根式,不能与 合并的是________(填
序号).
②⑤
针对练习
例1 计算:
最简二次根式
被开方数相同的二次根式
合并
一化,二找,三合并
典型例题
不能合并
例2 计算:
典型例题
二次根式加减运算的一般步骤
1.化:将每个二次根式都化成最简二次根式;
2.找:找出被开方数相同的二次根式;
3.合:将被开方数相同的二次根式合并成一项.
探究新知
计算后根号外的因数是分数的要写成假分数形式,不能写成带分数形式.
计算:
+-(-).
针对练习
思考:(2)中被开方数有小数,该怎样计算?
将被开方数中的小数化为分数,再进行计算.
二次根式的乘除与加减的对比
02
运算 二次根式的乘除 二次根式的加减
系数
被开方数
化简
二次根式的乘除与二次根式的加减的对比
系数相乘除
系数相加减
被开方数相乘除
被开方数不变
结果化为最简
二次根式
先化为最简二次根式,再合并被开方数相同的二次根式
探究新知
二次根式加减的应用
03
例3 已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成
三角形,求出其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:∵ 即a<c<b,
又∵ ∴a+c>b,
∴能构成三角形,周长为
分析:(1)若几个非负数的和为零,则这几个非负数必须为零;(2)根据三角形的三边关系来判断.
典型例题
例4 有一个等腰三角形的两边长分别为
,求其周长.
解: 当腰长为 时,
∵
∴此时能构成三角形,周长为
当腰长为 时,
∵
∴此时能构成三角形,周长为
典型例题
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
课堂练习
法则
步骤
同类二次根式(选学)
二次根式的加减
一般地,二次根式加减时,
可以先将二次根式化简成最简二次根式,
再将被开方数相同的二次根式进行合并.
一化,二找,三合并.
几个二次根式化成最简二次根式后,若被开方数相同,则这几个二次根式就是同类二次根式.
课堂小结
感谢观看
