28.1数据整理与表示 课件(共26张PPT)
文档属性
| 名称 | 28.1数据整理与表示 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 19:44:55 | ||
图片预览





文档简介
(共26张PPT)
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 28 章 统计初步
28.1数据整理与表示
学习目标
1.知道条形图、折线图、扇形图各自的优势;
2.会用表格和条形图、折线图、扇形图整理与表示数据;
3.会从图表中正确获取各种有用信息,解决实际问题.
生活中,我们经常碰到各种数据,如下列问题中的(1)、(2)、(3).这些数据传递了许多信息,有助于我们了解事实、分析情况和做出判断.
下列数据能否用表格或图形表示出来?
(1)在2000年第五次全国人口普查中,关于我国公民受教育状况的调查结果是:
每1000人中具有初中文化程度的约有340人,具有高中文化程度的约有111人,具
有大学文化程度的约有36人.
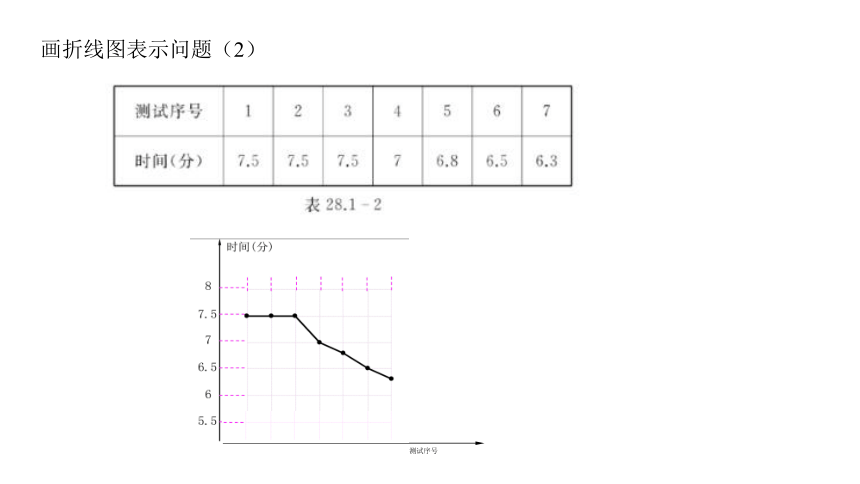
(2)某学生每天进行1500米跑运动.一个阶段内的七次测试情况是:前三次每次
跑完全程各用时7分30秒,第四次用时7分钟,第五次用时6分48秒,第六次用时6
分30秒,第七次用时6分18秒.
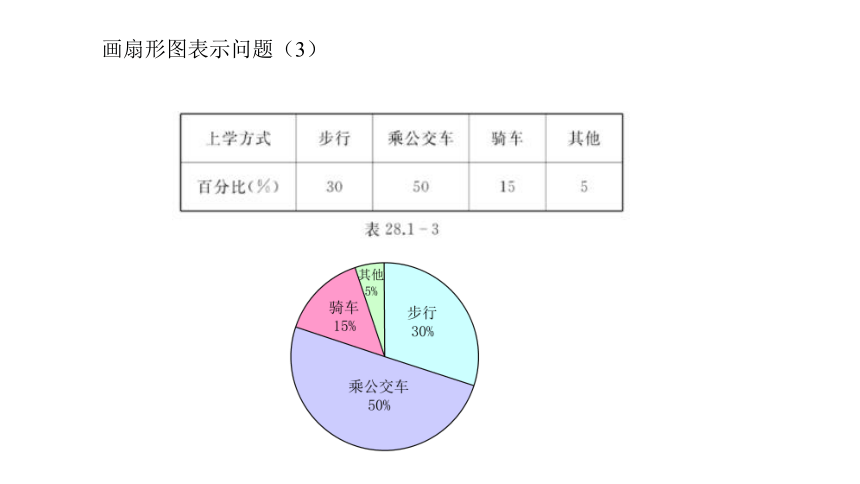
(3) 据调查,某校九年级有300名学生,其中30%的学生步行上学,50%的学生乘
公交车上学,15%的学生骑车上学,其余的学生用其他交通工具上学.
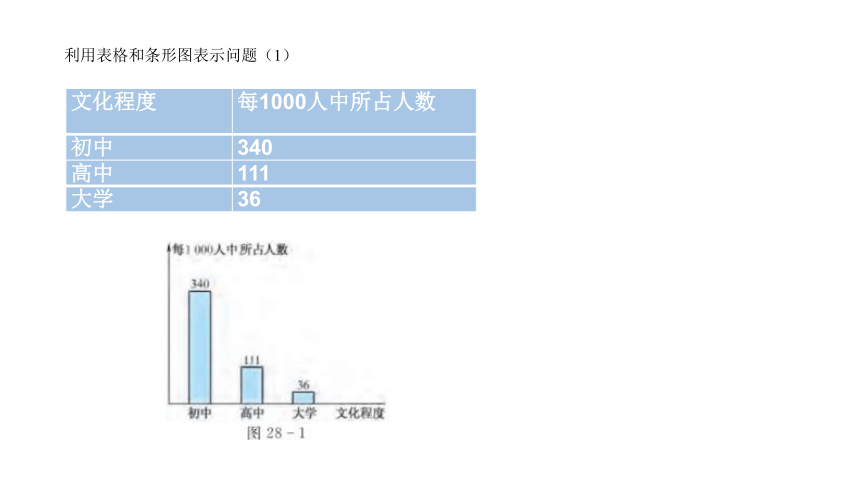
利用表格和条形图表示问题(1)
文化程度 每1000人中所占人数
初中 340
高中 111
大学 36
0
测试序号
1
2
3
4
5
6
7
画折线图表示问题(2)
画扇形图表示问题(3)
表和图简称为统计图表。其中条形图、折线图、扇形图是现实生活中常用的统计图表.
思考:条形图、折线图、扇形图的各自有何优势
总结:1.条形图有利于比较数据的差异
2.折线图可以直观地反映出数据变化的趋势;
3.扇形图可以凸现由数据所体现出来的部分与整体的关系
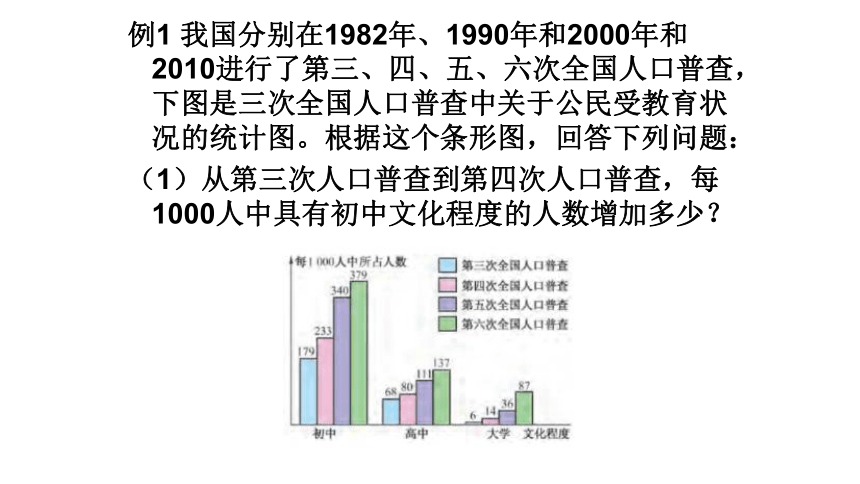
例1 我国分别在1982年、1990年和2000年和2010进行了第三、四、五、六次全国人口普查,下图是三次全国人口普查中关于公民受教育状况的统计图。根据这个条形图,回答下列问题:
(1)从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加多少?
问题1:每一次人口普查中,每1000人中具有初中、高中、大学文化程度的各有多少人?那么从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加多少?
解:233-179=54(人)
答:从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加54人.
例1 我国分别在1982年、1990年和2000年和2010进行了第三、四、五、六次全国人口普查,下图是三次全国人口普查中关于公民受教育状况的统计图。根据这个条形图,回答下列问题:
(2)从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加多少?
问题2:从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加多少人?
111-80=31(人)
答:从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加31人.
例1 我国分别在1982年、1990年和2000年和2010进行了第三、四、五、六次全国人口普查,下图是三次全国人口普查中关于公民受教育状况的统计图。根据这个条形图,回答下列问题:
(3)从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加几人?从2000年到2010年呢?
问题3:从1982年(第三次人口普查)到1990年(第四次人口普查)经过了多少年?大学人数增加多少人?平均每年增加多少人呢?
(14-6)÷8=1(人)
答:从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加1人.
问题4:从1990年(第四次人口普查)到2000年(第五次人口普查)经过了多少年?大学人数增加多少人?平均每年增加多少人呢?
(87-36)÷10=5.1(人)
答:从2000年到2010年具有大学文化程度的人数平均每年增加5.1人.
例2.某企业对七月份的产值分配作了如下两个统计图,结合图形回答下列问题:
(1)该企业七月份的产值是多少万元?管理成本是多少?
(2)请将两图中缺少的部分补完整。
金额(万元)
36
24
20
生产成本
45%
项目
管理成本
30%
税前利润
生产成本
管理成本
税前利润
( )%
25
问题1:从给出的条形图和扇形图可获得那些相关信息?由获得的信息可求七月份的总产值吗?如何求管理成本?
解:(1)36÷45﹪=80(万元)
80-36-20=24(万元)
答: 该企业七月份的产值是80万元,管理成本是24万元.
问题2:如何计算税前利润所占的百分比呢
1-45﹪-30﹪=25﹪
课本练习
随堂检测
1.填空:
常用的统计图有_____、____、 _____
1)条形图有利于__________,
2)折线图可以___________,
3)扇形图凸显了___________.
条形图
折线图
扇形图
比较数据的差距
直观地反映数据变化的趋势
由数据的部分与整体的关系
2.如图是某校七年级学生到校方式的情况的条形
统计图,下列说法正确的是( )
A.步行人数最少,只有90人
B.步行人数占总人数的60%
C.坐公共汽车的人数占总人数的50%
D.步行与骑自行车的人数和比坐公共汽车的人要少
【解析】从条形统计图可看出,步行人数是60人,骑自行车的人数是90人,坐公共汽车的人数是150人,因此C说法是正确的.故选C.
C
3.小梅所在学校七年级共有女生200人,她为了了解她所在学校七年级女生的身体发育情况,到校卫生室的体检表中随机抽取20名女生的身高,记录如下(单位:厘米):
165,161,161,156,157,161,151,
163,151,157,159,162,165,157,
163,156,157,169,151,153
请你帮小梅对上述数据进行分组整理;
身高(单位:厘米) 数据 人数 百分比(%)
150~154 151,151,151,153 4 20
155~159 156,157,157,159,157,156,157 7 35
160~164 161,161,161, 163,162,163 6 30
165~169 165,165,169 3 15
解:
数据的收集
1、普查:为某一特定目的而作的全面调查叫做普查。
2、抽样调查:从总体中抽取部分个体进行调查的方法叫做抽样调查。
把所要调查对象的全体叫做总体。
其中每一个调查对象叫做个体。
从总体中抽取的一部分个体叫做总体的一个样本。
样本中个体的数量叫做样本容量。
普查
抽样调查
优点
缺点
结果准确
工作量大,费时费力
有误差
省时省力
为了减少误差,样本需要随机抽取,随机抽取的样本叫做随机样本.
随机样本具有代表性。
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 28 章 统计初步
28.1数据整理与表示
学习目标
1.知道条形图、折线图、扇形图各自的优势;
2.会用表格和条形图、折线图、扇形图整理与表示数据;
3.会从图表中正确获取各种有用信息,解决实际问题.
生活中,我们经常碰到各种数据,如下列问题中的(1)、(2)、(3).这些数据传递了许多信息,有助于我们了解事实、分析情况和做出判断.
下列数据能否用表格或图形表示出来?
(1)在2000年第五次全国人口普查中,关于我国公民受教育状况的调查结果是:
每1000人中具有初中文化程度的约有340人,具有高中文化程度的约有111人,具
有大学文化程度的约有36人.
(2)某学生每天进行1500米跑运动.一个阶段内的七次测试情况是:前三次每次
跑完全程各用时7分30秒,第四次用时7分钟,第五次用时6分48秒,第六次用时6
分30秒,第七次用时6分18秒.
(3) 据调查,某校九年级有300名学生,其中30%的学生步行上学,50%的学生乘
公交车上学,15%的学生骑车上学,其余的学生用其他交通工具上学.
利用表格和条形图表示问题(1)
文化程度 每1000人中所占人数
初中 340
高中 111
大学 36
0
测试序号
1
2
3
4
5
6
7
画折线图表示问题(2)
画扇形图表示问题(3)
表和图简称为统计图表。其中条形图、折线图、扇形图是现实生活中常用的统计图表.
思考:条形图、折线图、扇形图的各自有何优势
总结:1.条形图有利于比较数据的差异
2.折线图可以直观地反映出数据变化的趋势;
3.扇形图可以凸现由数据所体现出来的部分与整体的关系
例1 我国分别在1982年、1990年和2000年和2010进行了第三、四、五、六次全国人口普查,下图是三次全国人口普查中关于公民受教育状况的统计图。根据这个条形图,回答下列问题:
(1)从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加多少?
问题1:每一次人口普查中,每1000人中具有初中、高中、大学文化程度的各有多少人?那么从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加多少?
解:233-179=54(人)
答:从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加54人.
例1 我国分别在1982年、1990年和2000年和2010进行了第三、四、五、六次全国人口普查,下图是三次全国人口普查中关于公民受教育状况的统计图。根据这个条形图,回答下列问题:
(2)从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加多少?
问题2:从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加多少人?
111-80=31(人)
答:从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加31人.
例1 我国分别在1982年、1990年和2000年和2010进行了第三、四、五、六次全国人口普查,下图是三次全国人口普查中关于公民受教育状况的统计图。根据这个条形图,回答下列问题:
(3)从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加几人?从2000年到2010年呢?
问题3:从1982年(第三次人口普查)到1990年(第四次人口普查)经过了多少年?大学人数增加多少人?平均每年增加多少人呢?
(14-6)÷8=1(人)
答:从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加1人.
问题4:从1990年(第四次人口普查)到2000年(第五次人口普查)经过了多少年?大学人数增加多少人?平均每年增加多少人呢?
(87-36)÷10=5.1(人)
答:从2000年到2010年具有大学文化程度的人数平均每年增加5.1人.
例2.某企业对七月份的产值分配作了如下两个统计图,结合图形回答下列问题:
(1)该企业七月份的产值是多少万元?管理成本是多少?
(2)请将两图中缺少的部分补完整。
金额(万元)
36
24
20
生产成本
45%
项目
管理成本
30%
税前利润
生产成本
管理成本
税前利润
( )%
25
问题1:从给出的条形图和扇形图可获得那些相关信息?由获得的信息可求七月份的总产值吗?如何求管理成本?
解:(1)36÷45﹪=80(万元)
80-36-20=24(万元)
答: 该企业七月份的产值是80万元,管理成本是24万元.
问题2:如何计算税前利润所占的百分比呢
1-45﹪-30﹪=25﹪
课本练习
随堂检测
1.填空:
常用的统计图有_____、____、 _____
1)条形图有利于__________,
2)折线图可以___________,
3)扇形图凸显了___________.
条形图
折线图
扇形图
比较数据的差距
直观地反映数据变化的趋势
由数据的部分与整体的关系
2.如图是某校七年级学生到校方式的情况的条形
统计图,下列说法正确的是( )
A.步行人数最少,只有90人
B.步行人数占总人数的60%
C.坐公共汽车的人数占总人数的50%
D.步行与骑自行车的人数和比坐公共汽车的人要少
【解析】从条形统计图可看出,步行人数是60人,骑自行车的人数是90人,坐公共汽车的人数是150人,因此C说法是正确的.故选C.
C
3.小梅所在学校七年级共有女生200人,她为了了解她所在学校七年级女生的身体发育情况,到校卫生室的体检表中随机抽取20名女生的身高,记录如下(单位:厘米):
165,161,161,156,157,161,151,
163,151,157,159,162,165,157,
163,156,157,169,151,153
请你帮小梅对上述数据进行分组整理;
身高(单位:厘米) 数据 人数 百分比(%)
150~154 151,151,151,153 4 20
155~159 156,157,157,159,157,156,157 7 35
160~164 161,161,161, 163,162,163 6 30
165~169 165,165,169 3 15
解:
数据的收集
1、普查:为某一特定目的而作的全面调查叫做普查。
2、抽样调查:从总体中抽取部分个体进行调查的方法叫做抽样调查。
把所要调查对象的全体叫做总体。
其中每一个调查对象叫做个体。
从总体中抽取的一部分个体叫做总体的一个样本。
样本中个体的数量叫做样本容量。
普查
抽样调查
优点
缺点
结果准确
工作量大,费时费力
有误差
省时省力
为了减少误差,样本需要随机抽取,随机抽取的样本叫做随机样本.
随机样本具有代表性。
