27.6正多边形与圆(第2课时) 课件(共22张PPT)
文档属性
| 名称 | 27.6正多边形与圆(第2课时) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 19:53:39 | ||
图片预览





文档简介
(共22张PPT)
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 27 章 圆与正多边形
27.6正多边形与圆(第2课时)
学习目标
1.能在以正多边形的一边为底、两条半径为腰的等腰三角形中将正多边形的 边长、半径长、边心距、中心角这四个量表示出来,渗透化归的数学思想.
2.会在正三角形、正方形、正六边形中进行简单的几何计算.
3.会利用等分圆周画正三角形、正四边形、正六边形.
如图,在正n边形中,分别经过各定点的半径将这个正n边形分为n个 三角形,每个等腰三角形的腰是正n边形的 ,底边是正n边形的 ,顶角是正n边形的 ,底边上的高是正n边形的 的半径,它的长是正n边形的边心距 。
等腰
半径
边
中心角
内切圆
边心距
设正n边形的半径长为 ,中心角为 ,边长为 ,边心距为 ,则利用等腰三角形OAB,通过解直角三角形OAH,可由其中两个量求出其余的两个量,进一步还可求出这个正n边形的周长和面积
复习引入
各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n (n ≥ 3)条边,
那么这个正多边形叫做正n 边形.
正多边形定义
下列命题中正确的有:
(1)菱形是正四边形(2)矩形是正四边形
(3)各边相等的三角形是正三角形
议一议:
1、将圆三等分,那么其中一等份的弧所对的圆心角是多少度?四等分、五等分、n等分呢?
2、你能用将圆分成五等分吗?
3、顺次连接五个分点,你得到怎样的图形
·
A
B
C
D
E
O
72°
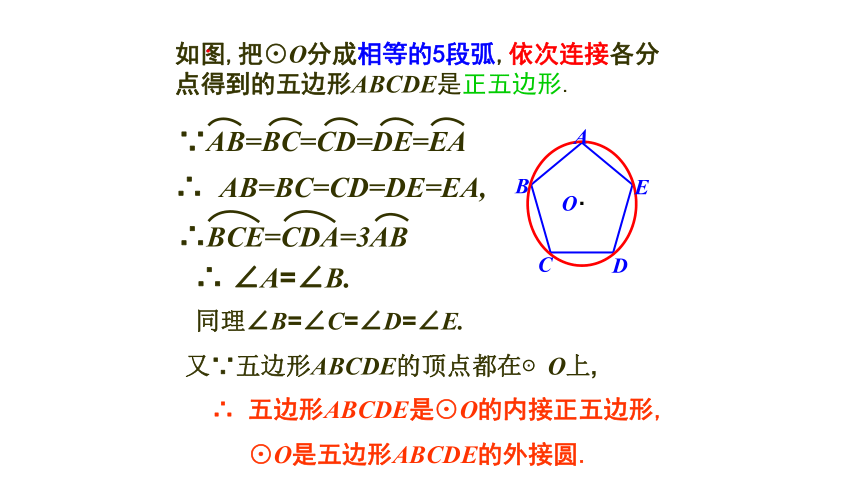
如图,把⊙O分成相等的5段弧,依次连接各分点得到的五边形ABCDE是正五边形.
∴ AB=BC=CD=DE=EA,
∴ ∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
又∵五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形,
⊙O是五边形ABCDE的外接圆.
.
∵AB=BC=CD=DE=EA
∴BCE=CDA=3AB
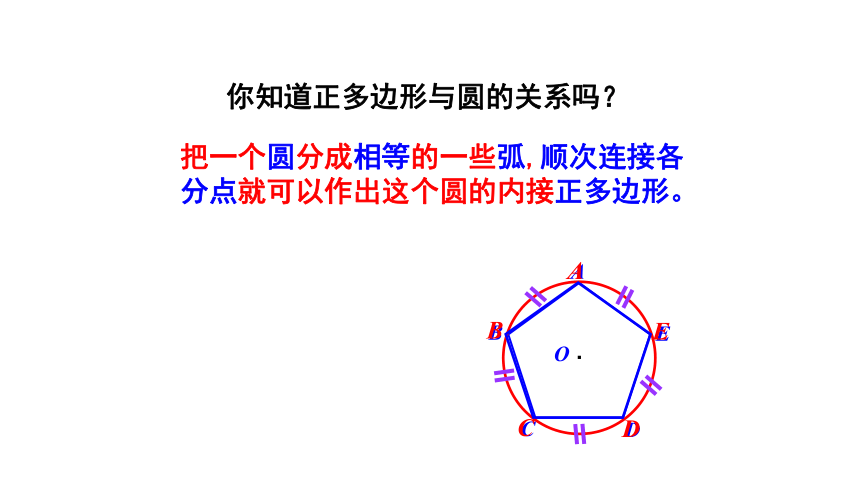
你知道正多边形与圆的关系吗?
把一个圆分成相等的一些弧,顺次连接各分点就可以作出这个圆的内接正多边形。
·
A
B
C
D
E
O
A
B
C
D
E
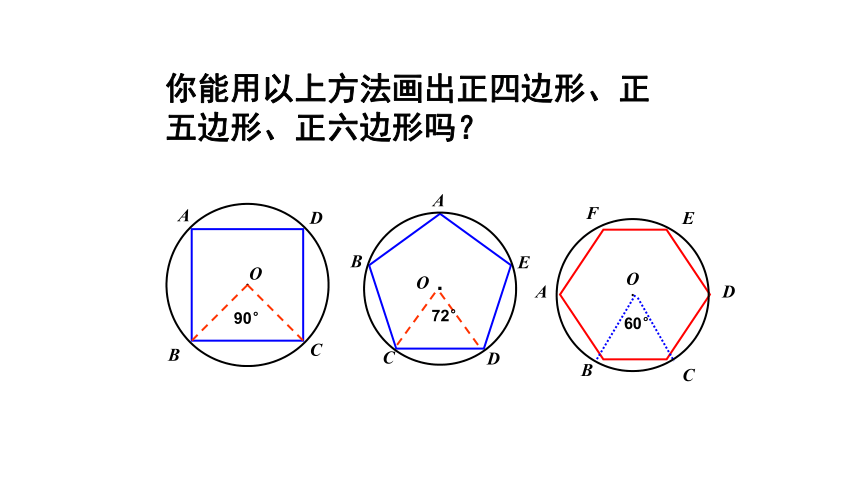
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
A
B
C
D
E
Q
R
S
P
T
O
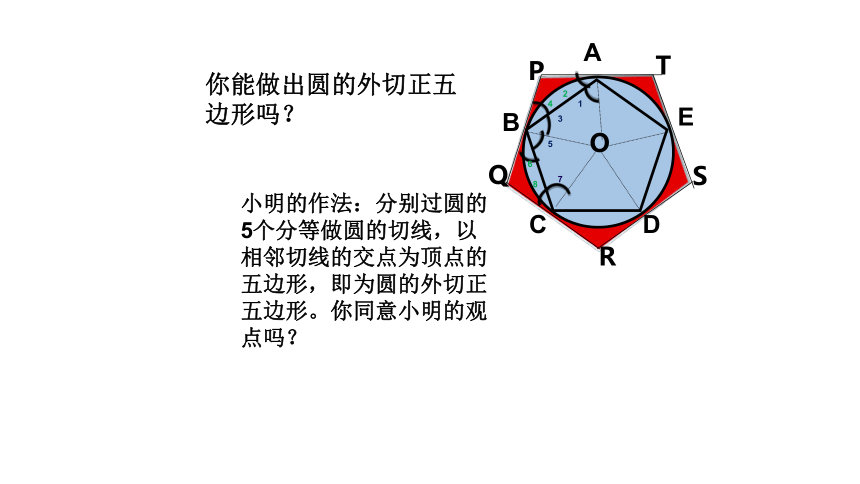
你能做出圆的外切正五边形吗?
小明的作法:分别过圆的5个分等做圆的切线,以相邻切线的交点为顶点的五边形,即为圆的外切正五边形。你同意小明的观点吗?
4
2
3
1
5
7
6
8
A
B
C
D
E
Q
R
S
P
T
O
4
2
3
1
5
7
6
8
在正五边形ABCD中由∠AOB= ∠BOC可得
∠1= ∠3= ∠5= ∠7,由PT、PQ是圆O的切线可知
∠1+ ∠ 2= ∠3+ ∠ 4= ∠5+ ∠ 6= ∠7+ ∠8
所以∠2= ∠4= ∠6= ∠8,PA=PB, QB=QC
在△APB和△BQC中
∵ ∠2= ∠6, ∠4= ∠8,AB=BC
∴ △APB≌△BQC(ASA)
∴PA=QB, ∠P= ∠Q
∴ PA=QB=PB=QC, 设PA=a,则PT=PQ=2a
同理可证五边形PQRST各边都等于2a,各角都相等
结论:经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边形。
你能尺规作出正四边形、正六边形、正三角形、正十二边形吗?
O
A
B
C
E
F
·
D
以半径长为单位 在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
1、作正四边形:在圆中作两条互相垂直的直径,依次连结四个端点则作出正四边形
先作出正四边形,则可作出正八边形、正十六边形……
你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么?
结论:
把圆分成n条相等的弧(n≥3)
⑴依次连结各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边
形.
定理:
正n边形的半径和边心距把正n边形分成2n 个全等的直角三角形.
定理的实质是把正多边形的问题向直角三角形转化.
由于这些直角三角形的斜边都是正n边形的半径R,一条直角边是正n边形的边心距rn,另一条直角边是正n边形边长an的一半,一个锐角是正n边形中心角的一半,所以,根据上面定理就可以把正n边形的有关计算归结为解直角三角形问题.
解:设正三角形的中心是点O,分别联结OA、OB;
作△OAB的高OD.
结论:
在正n边形中有:
在上述六个公式中,只要给定两个条件,就可以确定正多边形的其它元素.
; ; ;
; ; .
例2:已知圆O,试用直尺和圆规作圆O的内接正六边形
作法一:
1.在⊙O上任取一点A,以A为圆心,OA为半径作弧,在⊙O上依次截得点B、C、D、E、F(即将圆六等分).
2.顺次联结AB、BC、CD、DE、EF、FA.
六边形ABCDEF就是所求作的圆内接正六边形.
作法二:
1.作⊙O的直径
2.以A为圆心,AO为半径作弧,交⊙O于C、D两点
3.以B为圆心,BO为半径作弧,交⊙O于E、F两点
4.顺次联结AD、DF、FB、BE、EC、CA
课本练习
随堂检测
1. 已知正六边形ABCDEF的半径为R,求这个正六边
形的边长、周长P6和面积S6.
解:作半径OA、OB;作OG⊥AB,
垂足为G,得Rt△OGB.
∵∠AOB= ,
∴a6 =2·Rsin30°=R,
∴P6=6·a6=6R,
∵r6=Rcos30°= ,
∴
∴∠GOB=
A
B
C
D
E
Q
R
S
P
T
O
4
2
3
1
5
7
6
8
在正五边形ABCD中由∠AOB= ∠BOC可得
∠1= ∠3= ∠5= ∠7,由PT、PQ是圆O的切线可知
∠1+ ∠ 2= ∠3+ ∠ 4= ∠5+ ∠ 6= ∠7+ ∠8
所以∠2= ∠4= ∠6= ∠8,PA=PB, QB=QC
在△APB和△BQC中
∵ ∠2= ∠6, ∠4= ∠8,AB=BC
∴ △APB≌△BQC(ASA)
∴PA=QB, ∠P= ∠Q
∴ PA=QB=PB=QC, 设PA=a,则PT=PQ=2a
同理可证五边形PQRST各边都等于2a,各角都相等
2.做出圆的外切正五边形
画正多边形的方法
1.用量角器等分圆
2.量角器和圆规等分圆
3.尺规作图等分圆
课堂小结
2022-2023学年九年级数学下册同步精品课堂(沪教版)
第 27 章 圆与正多边形
27.6正多边形与圆(第2课时)
学习目标
1.能在以正多边形的一边为底、两条半径为腰的等腰三角形中将正多边形的 边长、半径长、边心距、中心角这四个量表示出来,渗透化归的数学思想.
2.会在正三角形、正方形、正六边形中进行简单的几何计算.
3.会利用等分圆周画正三角形、正四边形、正六边形.
如图,在正n边形中,分别经过各定点的半径将这个正n边形分为n个 三角形,每个等腰三角形的腰是正n边形的 ,底边是正n边形的 ,顶角是正n边形的 ,底边上的高是正n边形的 的半径,它的长是正n边形的边心距 。
等腰
半径
边
中心角
内切圆
边心距
设正n边形的半径长为 ,中心角为 ,边长为 ,边心距为 ,则利用等腰三角形OAB,通过解直角三角形OAH,可由其中两个量求出其余的两个量,进一步还可求出这个正n边形的周长和面积
复习引入
各边相等,各角也相等的多边形是正多边形.
正n 边形:如果一个正多边形有n (n ≥ 3)条边,
那么这个正多边形叫做正n 边形.
正多边形定义
下列命题中正确的有:
(1)菱形是正四边形(2)矩形是正四边形
(3)各边相等的三角形是正三角形
议一议:
1、将圆三等分,那么其中一等份的弧所对的圆心角是多少度?四等分、五等分、n等分呢?
2、你能用将圆分成五等分吗?
3、顺次连接五个分点,你得到怎样的图形
·
A
B
C
D
E
O
72°
如图,把⊙O分成相等的5段弧,依次连接各分点得到的五边形ABCDE是正五边形.
∴ AB=BC=CD=DE=EA,
∴ ∠A=∠B.
·
A
B
C
D
E
O
同理∠B=∠C=∠D=∠E.
又∵五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCDE是⊙O的内接正五边形,
⊙O是五边形ABCDE的外接圆.
.
∵AB=BC=CD=DE=EA
∴BCE=CDA=3AB
你知道正多边形与圆的关系吗?
把一个圆分成相等的一些弧,顺次连接各分点就可以作出这个圆的内接正多边形。
·
A
B
C
D
E
O
A
B
C
D
E
你能用以上方法画出正四边形、正五边形、正六边形吗?
·
A
B
C
D
O
·
A
B
C
D
E
O
O
A
B
C
D
E
F
·
90°
72°
60°
A
B
C
D
E
Q
R
S
P
T
O
你能做出圆的外切正五边形吗?
小明的作法:分别过圆的5个分等做圆的切线,以相邻切线的交点为顶点的五边形,即为圆的外切正五边形。你同意小明的观点吗?
4
2
3
1
5
7
6
8
A
B
C
D
E
Q
R
S
P
T
O
4
2
3
1
5
7
6
8
在正五边形ABCD中由∠AOB= ∠BOC可得
∠1= ∠3= ∠5= ∠7,由PT、PQ是圆O的切线可知
∠1+ ∠ 2= ∠3+ ∠ 4= ∠5+ ∠ 6= ∠7+ ∠8
所以∠2= ∠4= ∠6= ∠8,PA=PB, QB=QC
在△APB和△BQC中
∵ ∠2= ∠6, ∠4= ∠8,AB=BC
∴ △APB≌△BQC(ASA)
∴PA=QB, ∠P= ∠Q
∴ PA=QB=PB=QC, 设PA=a,则PT=PQ=2a
同理可证五边形PQRST各边都等于2a,各角都相等
结论:经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边形。
你能尺规作出正四边形、正六边形、正三角形、正十二边形吗?
O
A
B
C
E
F
·
D
以半径长为单位 在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
1、作正四边形:在圆中作两条互相垂直的直径,依次连结四个端点则作出正四边形
先作出正四边形,则可作出正八边形、正十六边形……
你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么?
结论:
把圆分成n条相等的弧(n≥3)
⑴依次连结各分点所得的多边形是这个圆的
内接正多边形;
⑵经过各分点作圆的切线,以相邻切线的交
点为顶点的多边形是这个圆的外切正多边
形.
定理:
正n边形的半径和边心距把正n边形分成2n 个全等的直角三角形.
定理的实质是把正多边形的问题向直角三角形转化.
由于这些直角三角形的斜边都是正n边形的半径R,一条直角边是正n边形的边心距rn,另一条直角边是正n边形边长an的一半,一个锐角是正n边形中心角的一半,所以,根据上面定理就可以把正n边形的有关计算归结为解直角三角形问题.
解:设正三角形的中心是点O,分别联结OA、OB;
作△OAB的高OD.
结论:
在正n边形中有:
在上述六个公式中,只要给定两个条件,就可以确定正多边形的其它元素.
; ; ;
; ; .
例2:已知圆O,试用直尺和圆规作圆O的内接正六边形
作法一:
1.在⊙O上任取一点A,以A为圆心,OA为半径作弧,在⊙O上依次截得点B、C、D、E、F(即将圆六等分).
2.顺次联结AB、BC、CD、DE、EF、FA.
六边形ABCDEF就是所求作的圆内接正六边形.
作法二:
1.作⊙O的直径
2.以A为圆心,AO为半径作弧,交⊙O于C、D两点
3.以B为圆心,BO为半径作弧,交⊙O于E、F两点
4.顺次联结AD、DF、FB、BE、EC、CA
课本练习
随堂检测
1. 已知正六边形ABCDEF的半径为R,求这个正六边
形的边长、周长P6和面积S6.
解:作半径OA、OB;作OG⊥AB,
垂足为G,得Rt△OGB.
∵∠AOB= ,
∴a6 =2·Rsin30°=R,
∴P6=6·a6=6R,
∵r6=Rcos30°= ,
∴
∴∠GOB=
A
B
C
D
E
Q
R
S
P
T
O
4
2
3
1
5
7
6
8
在正五边形ABCD中由∠AOB= ∠BOC可得
∠1= ∠3= ∠5= ∠7,由PT、PQ是圆O的切线可知
∠1+ ∠ 2= ∠3+ ∠ 4= ∠5+ ∠ 6= ∠7+ ∠8
所以∠2= ∠4= ∠6= ∠8,PA=PB, QB=QC
在△APB和△BQC中
∵ ∠2= ∠6, ∠4= ∠8,AB=BC
∴ △APB≌△BQC(ASA)
∴PA=QB, ∠P= ∠Q
∴ PA=QB=PB=QC, 设PA=a,则PT=PQ=2a
同理可证五边形PQRST各边都等于2a,各角都相等
2.做出圆的外切正五边形
画正多边形的方法
1.用量角器等分圆
2.量角器和圆规等分圆
3.尺规作图等分圆
课堂小结
