【班海精品】北师大版(新)七下-2.2探索直线平行的条件 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-2.2探索直线平行的条件 第一课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:28 | ||
图片预览








文档简介
(共52张PPT)
2.2探索直线平行的条件
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
日常生活中,人们经常用到平行线.如图,装修工人
正在向墙上钉木条.如果木条b 与墙壁边缘垂直,那么木
条a 与墙壁边缘所成的角为多少度时,
才能使木条a 与木条b 平行?
你知道其中的理由吗?
如果木条b 不与墙壁边缘垂直呢?
新课精讲
探索新知
1
知识点
同位角
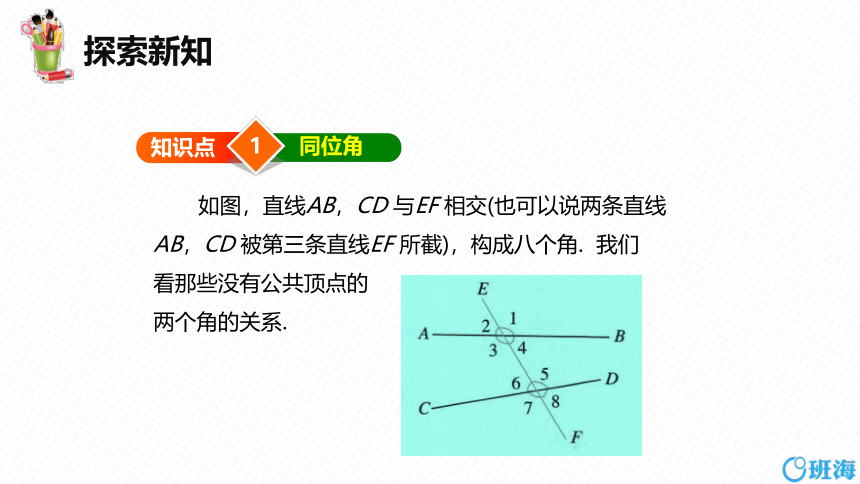
如图,直线AB,CD 与EF 相交(也可以说两条直线
AB,CD 被第三条直线EF 所截),构成八个角. 我们
看那些没有公共顶点的
两个角的关系.
探索新知
A
B
C
D
F
2
3
6
7
8
4
1
5
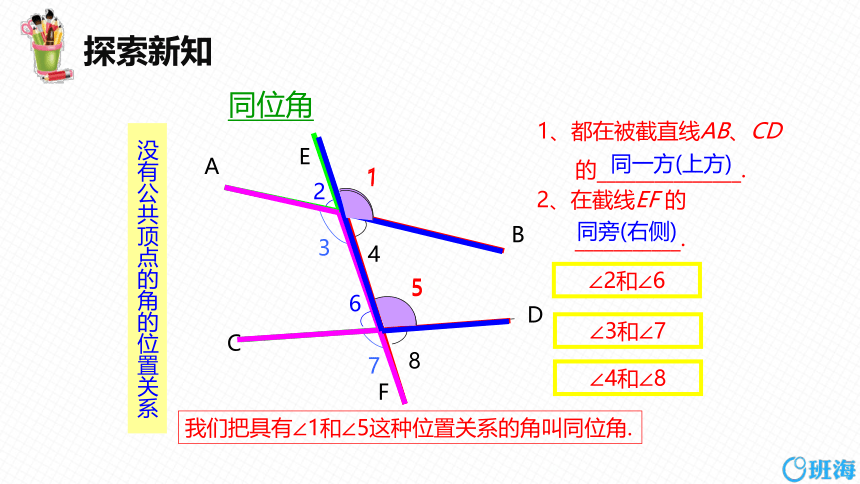
同位角
没有公共顶点的角的位置关系
E
1、都在被截直线AB、CD
的_______________.
2、在截线EF 的
___________.
同一方(上方)
同旁(右侧)
∠2和∠6
∠3和∠7
∠4和∠8
1
5
我们把具有∠1和∠5这种位置关系的角叫同位角.
探索新知
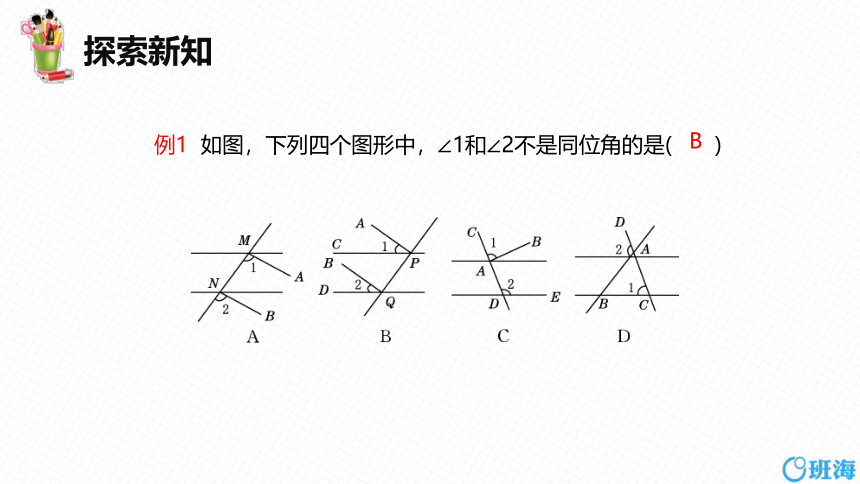
例1 如图,下列四个图形中,∠1和∠2不是同位角的是( )
B
探索新知
导引:根据同位角的概念,找出“三线”之后再看是否为
“F”形即可判定.选项B中的∠1与∠2的边有四条,
分别为PA,PC,QB,QD,不满足“三线”的条
件,故选项B中的∠1与∠2不是同位角;其他A,C,
D三项中的∠1,∠2均满足同位角的条件,故选B.
探索新知
总 结
判断“三线八角”中的两个角的位置关系时,必
须找出“哪两条直线被第三条直线所截”,即找准截
线是关键,找截线的实质就是找到相应两个角的顶点
所在的直线,如果这两个角的公共边恰好就是截线,
那么这两个角就是同位角.
典题精讲
1
如图,已知直线a,b 被直线c 所截,那么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
D
典题精讲
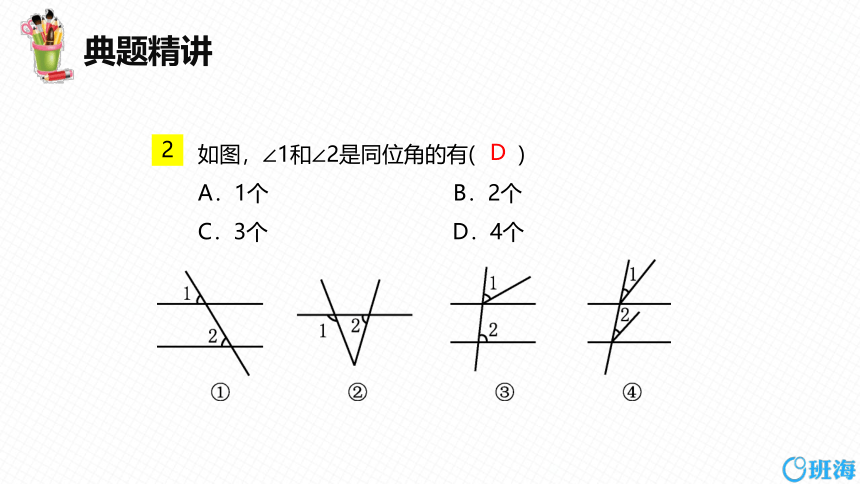
如图,∠1和∠2是同位角的有( )
A.1个 B.2个
C.3个 D.4个
D
2
探索新知
知识点
同位角相等,两直线平行
做一做
如图,三根木条相交成∠1,∠2,固定木条b,c 转动木条a.
如图,在木条a 的转动过程中,观察∠2的变化以及它
与∠1的大小关系,你发现木条a 与木条b 的位置关系发生
了什么变化?木条a 何时与木条b 平行?
2
探索新知
改变图中∠1的大小,按照上面的方式再做一
做. ∠1与∠2的大小满足什么关系时,木条a 与木
条b 平行?与同伴进行交流.
探索新知
请按下图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法可以看做是怎
样的图形变换
(2)把图中的直线l1,l2 看成被
尺边AB 所截,那么在画图过
程中,什么角始终保持相等?
平移变换
同位角
由此你能发现判定两直线平行的方法吗?
探索新知
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
探索新知
例2
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
要判定哪两条直线平行,就是要确定∠1,∠2是哪
两条直线被第三条直线所截得到的同位角,即找出
∠1,∠2除公共边外的另两边.
导引:
C
探索新知
利用同位角相等来判定两直线平行的方法:
(1)找出这对同位角是哪两条直线被第三条直线所截形成的;
(2)根据“同位角相等,两直线平行”推导出这两条直线平行.
总 结
探索新知
例3
如图,已知直线AB,CD 被直线EF 所截,∠1+∠2=180°. AB 与CD 平行吗?请说明理由.
要说明AB 与CD 平行,需找出AB,
CD 被第三条直线所截形成的一组
同位角相等,即要说明∠1=∠3
即可;要说明∠1=∠3,由于已
知∠1+∠2=180°,因此只需说明∠2+∠3=180°
即可,这可由补角定义得出.
导引:
探索新知
AB∥CD. 理由如下:
因为∠1+∠2=180°(已知),
∠2+∠3=180°(补角定义),
所以∠1=∠3(同角的补角相等).
所以AB∥CD (同位角相等,两直线平行).
解:
探索新知
判断两条直线是否平行,可以找出这两条直线
被第三条直线所截得到的一对同位角,并利用相关
角的条件判断其是否相等,如果相等,那么这两条
直线平行.
总 结
典题精讲
找出下面点阵(点阵中相邻的四个点构成正方形)中互相平行的线段.
1
解:AB∥CD,EF∥GH.
理由:“同位角相等,两直线平行”.
典题精讲
如图,∠1 = ∠2 = 55°,
直线AB 与CD 平行吗?
2
AB∥CD.
理由:如图,∠3=∠2,又因为∠1=∠2=55°,所以∠3=∠2=55°,所以∠1=∠3,所以AB∥CD (同位角相等,两直线平行).
解:
典题精讲
如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB_______CD.
3
∥
典题精讲
如图,直线AB,CD 被直线EF 所截,∠1=55°,下列条件中能判定AB∥CD 的是( )
A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125°
4
D
探索新知
3
知识点
平行存在唯一性
经过点C 可以画几条直
线与直线AB 平行?
A
B
a
b
(2) 过点D 画一条直线与
AB 平行.
(3) 通过画图,你发
现了什么?
经过直线外一点,有且只有一条直线与这条直线平行;
C
D
探索新知
例4 下列说法:
①过一点有且只有一条直线与已知直线平行;
②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条直线平行.
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
导引:过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C
探索新知
对于此类辨析题,要正确解答,必须要抓住
相关的内容,特别是关键字词及其重要特征,要
在比较中理解,再在理解的基础上进行记忆.
总 结
典题精讲
对于同一平面内的直线a,b,c,如果a 与b 平行,c 与a 相交,那么c 与b 的位置关系是相交还是平行?
1
相交.
解:
典题精讲
过一点画已知直线的平行线时( )
A.有且只有一条
B.有两条
C.不存在
D.不存在或只有一条
2
D
探索新知
4
知识点
平行线的传递性
平行公理的推论:如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.简称:同平行于
第三条直线的两直线平行.
表达方式:如果a∥c,b∥c,那么a∥b.
平行公理的推论:可用来判定两直线平行.
探索新知
例5
如图,P 是三角形ABC 内部任意一点.
(1)过P 点向左画射线PM∥BC 交AB 于点M,过P 点向
右画射线PN∥BC 交AC 于点N;
(2)在(1)中画出的图形中,∠MPN 的度数一定等于
180°,你能说明其中的道理吗?
探索新知
在(1)中,按照过直线外一点画已知直线的平行线的方
法画图即可.在(2)中,要说明∠MPN=180°,可转
化为说明点M,P,N 在同一条直线上.
导引:
(1)画出的射线PM,PN,如图.
(2)因为射线PM∥BC,射线
PN∥BC,所以直线PM∥BC,
直线PN∥BC.
根据平行线的基本性质1,可知直线PM 与直线PN 是
同一条直线,
即点M,P,N 在同一条直线上.所以∠MPN=180°.
解:
探索新知
本题运用转化思想,把说明∠MPN=180°转化
为说明点M,P,N 在同一条直线上,进而把问题转
化为利用平行线的基本性质说明直线PM 与直线PN
是同一条直线.
总 结
典题精讲
在每一步推理后面的括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,所以AB∥EF
(____________________________________).
(2)如图②,因为AB∥CD,过点F 作EF∥AB
(____________________________________________________),
所以EF∥CD (____________________________________).
1
过直线外一点,有且只有一条直线与这条直线平行
平行于同一条直线的两条直线平行
平行于同一条直线的两条直线平行
典题精讲
下列说法中,错误的有( )
①若a 与c 相交,b 与c 相交,则a 与b 相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
2
B
易错提醒
某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,则这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次左拐50°,第二次左拐130°
易错点:混淆两角的位置关系,画不出图形而致错
A
学以致用
小试牛刀
如图,能判定EB∥AC 的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
1
D
小试牛刀
下列说法正确的是( )
A.两条不相交的直线叫做平行线
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行
D.在同一平面内不相交的两条直线叫做平行线
D
2
小试牛刀
3
如图,点B 在DC 上,BE 平分∠ABD,∠ABE=∠C,试说
明:BE∥AC.解:因为BE 平分∠ABD,
所以∠ABE=∠DBE
(___________________).
因为∠ABE=∠C,
所以∠DBE=∠C.
所以BE∥AC (____________________________).
角平分线的定义
同位角相等,两直线平行
如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以______∥______(同位角相等,两直线平行).
(2)因为∠3+∠4=180°(平角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4.
所以______∥_____(同位角相等,两直线平行).
小试牛刀
4
a
b
c
b
小试牛刀
5
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(_______),
所以a∥b (__________________________).
因为∠3=∠4(_________),
所以b∥c (_________________________).
所以a∥c (____________________________________).
已知
同位角相等,两直线平行
平行于同一条直线的两条直线平行
已知
同位角相等,两直线平行
小试牛刀
6
如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明.
(2)方法二:用“第三直线”说明.
小试牛刀
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.
所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
解:
小试牛刀
7
在同一平面内,已知A,B,C 是直线l 同旁的三个点.
(1)如果AB∥l,BC∥l,那么A,B,C 三点在同一条直线上
吗?为什么?
(2)如果AB⊥l,BC⊥l,那么A,B,C 三点在同一条直线上
吗?为什么?
小试牛刀
(1)在同一条直线上,因为直线AB,BC 都经过点B,且都与直线 l 平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC 为同一条直线.所以A,B,C 三点在同一条直线上.
(2)在同一条直线上,因为AB,BC 都经过点B,且都与直线 l 垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC 为同一条直线.所以A,B,C 三点在同一条直线上.
解:
小试牛刀
8
如图,∠ABC=∠ACB,BD 平分∠ABC,CE 平分∠ACB,
∠DBF=∠F,问:CE 与DF 的位置关系怎样?试说明理由.
小试牛刀
CE∥DF.理由如下:
因为BD 平分∠ABC,CE 平分∠ACB,
所以∠DBC= ∠ABC,∠BCE= ∠ACB.
因为∠ABC=∠ACB,所以∠DBC=∠BCE.
因为∠DBF=∠F,所以∠BCE=∠F.
所以CE∥DF.
解:
课堂小结
课堂小结
1.平行线的判定方法:
(1)两条直线被另一条直线截得的同位角相等;
(2)两条直线同平行于第三条直线;
(3)在同一平面内,两条直线同垂直于第三条直线.
2.判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”(平行或垂直)判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.2探索直线平行的条件
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
日常生活中,人们经常用到平行线.如图,装修工人
正在向墙上钉木条.如果木条b 与墙壁边缘垂直,那么木
条a 与墙壁边缘所成的角为多少度时,
才能使木条a 与木条b 平行?
你知道其中的理由吗?
如果木条b 不与墙壁边缘垂直呢?
新课精讲
探索新知
1
知识点
同位角
如图,直线AB,CD 与EF 相交(也可以说两条直线
AB,CD 被第三条直线EF 所截),构成八个角. 我们
看那些没有公共顶点的
两个角的关系.
探索新知
A
B
C
D
F
2
3
6
7
8
4
1
5
同位角
没有公共顶点的角的位置关系
E
1、都在被截直线AB、CD
的_______________.
2、在截线EF 的
___________.
同一方(上方)
同旁(右侧)
∠2和∠6
∠3和∠7
∠4和∠8
1
5
我们把具有∠1和∠5这种位置关系的角叫同位角.
探索新知
例1 如图,下列四个图形中,∠1和∠2不是同位角的是( )
B
探索新知
导引:根据同位角的概念,找出“三线”之后再看是否为
“F”形即可判定.选项B中的∠1与∠2的边有四条,
分别为PA,PC,QB,QD,不满足“三线”的条
件,故选项B中的∠1与∠2不是同位角;其他A,C,
D三项中的∠1,∠2均满足同位角的条件,故选B.
探索新知
总 结
判断“三线八角”中的两个角的位置关系时,必
须找出“哪两条直线被第三条直线所截”,即找准截
线是关键,找截线的实质就是找到相应两个角的顶点
所在的直线,如果这两个角的公共边恰好就是截线,
那么这两个角就是同位角.
典题精讲
1
如图,已知直线a,b 被直线c 所截,那么∠1的同位角是( )
A.∠2
B.∠3
C.∠4
D.∠5
D
典题精讲
如图,∠1和∠2是同位角的有( )
A.1个 B.2个
C.3个 D.4个
D
2
探索新知
知识点
同位角相等,两直线平行
做一做
如图,三根木条相交成∠1,∠2,固定木条b,c 转动木条a.
如图,在木条a 的转动过程中,观察∠2的变化以及它
与∠1的大小关系,你发现木条a 与木条b 的位置关系发生
了什么变化?木条a 何时与木条b 平行?
2
探索新知
改变图中∠1的大小,按照上面的方式再做一
做. ∠1与∠2的大小满足什么关系时,木条a 与木
条b 平行?与同伴进行交流.
探索新知
请按下图所示方法画两条平行线,然后讨论下面的问题:
(1)上面的画法可以看做是怎
样的图形变换
(2)把图中的直线l1,l2 看成被
尺边AB 所截,那么在画图过
程中,什么角始终保持相等?
平移变换
同位角
由此你能发现判定两直线平行的方法吗?
探索新知
一般地,判断两直线平行有下面的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
探索新知
例2
如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
要判定哪两条直线平行,就是要确定∠1,∠2是哪
两条直线被第三条直线所截得到的同位角,即找出
∠1,∠2除公共边外的另两边.
导引:
C
探索新知
利用同位角相等来判定两直线平行的方法:
(1)找出这对同位角是哪两条直线被第三条直线所截形成的;
(2)根据“同位角相等,两直线平行”推导出这两条直线平行.
总 结
探索新知
例3
如图,已知直线AB,CD 被直线EF 所截,∠1+∠2=180°. AB 与CD 平行吗?请说明理由.
要说明AB 与CD 平行,需找出AB,
CD 被第三条直线所截形成的一组
同位角相等,即要说明∠1=∠3
即可;要说明∠1=∠3,由于已
知∠1+∠2=180°,因此只需说明∠2+∠3=180°
即可,这可由补角定义得出.
导引:
探索新知
AB∥CD. 理由如下:
因为∠1+∠2=180°(已知),
∠2+∠3=180°(补角定义),
所以∠1=∠3(同角的补角相等).
所以AB∥CD (同位角相等,两直线平行).
解:
探索新知
判断两条直线是否平行,可以找出这两条直线
被第三条直线所截得到的一对同位角,并利用相关
角的条件判断其是否相等,如果相等,那么这两条
直线平行.
总 结
典题精讲
找出下面点阵(点阵中相邻的四个点构成正方形)中互相平行的线段.
1
解:AB∥CD,EF∥GH.
理由:“同位角相等,两直线平行”.
典题精讲
如图,∠1 = ∠2 = 55°,
直线AB 与CD 平行吗?
2
AB∥CD.
理由:如图,∠3=∠2,又因为∠1=∠2=55°,所以∠3=∠2=55°,所以∠1=∠3,所以AB∥CD (同位角相等,两直线平行).
解:
典题精讲
如图,木工师傅利用直角尺在木板上画出两条线段,则线段AB_______CD.
3
∥
典题精讲
如图,直线AB,CD 被直线EF 所截,∠1=55°,下列条件中能判定AB∥CD 的是( )
A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125°
4
D
探索新知
3
知识点
平行存在唯一性
经过点C 可以画几条直
线与直线AB 平行?
A
B
a
b
(2) 过点D 画一条直线与
AB 平行.
(3) 通过画图,你发
现了什么?
经过直线外一点,有且只有一条直线与这条直线平行;
C
D
探索新知
例4 下列说法:
①过一点有且只有一条直线与已知直线平行;
②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条直线平行.
其中正确的有( )
A.3个 B.2个 C.1个 D.0个
导引:过直线外一点可以画一条直线与已知直线平行,
而过直线上一点画不出与该直线平行的直线;
一条直线的平行线有无数条,故只有③正确.
C
探索新知
对于此类辨析题,要正确解答,必须要抓住
相关的内容,特别是关键字词及其重要特征,要
在比较中理解,再在理解的基础上进行记忆.
总 结
典题精讲
对于同一平面内的直线a,b,c,如果a 与b 平行,c 与a 相交,那么c 与b 的位置关系是相交还是平行?
1
相交.
解:
典题精讲
过一点画已知直线的平行线时( )
A.有且只有一条
B.有两条
C.不存在
D.不存在或只有一条
2
D
探索新知
4
知识点
平行线的传递性
平行公理的推论:如果两条直线都与第三条直线平
行,那么这两条直线也互相平行.简称:同平行于
第三条直线的两直线平行.
表达方式:如果a∥c,b∥c,那么a∥b.
平行公理的推论:可用来判定两直线平行.
探索新知
例5
如图,P 是三角形ABC 内部任意一点.
(1)过P 点向左画射线PM∥BC 交AB 于点M,过P 点向
右画射线PN∥BC 交AC 于点N;
(2)在(1)中画出的图形中,∠MPN 的度数一定等于
180°,你能说明其中的道理吗?
探索新知
在(1)中,按照过直线外一点画已知直线的平行线的方
法画图即可.在(2)中,要说明∠MPN=180°,可转
化为说明点M,P,N 在同一条直线上.
导引:
(1)画出的射线PM,PN,如图.
(2)因为射线PM∥BC,射线
PN∥BC,所以直线PM∥BC,
直线PN∥BC.
根据平行线的基本性质1,可知直线PM 与直线PN 是
同一条直线,
即点M,P,N 在同一条直线上.所以∠MPN=180°.
解:
探索新知
本题运用转化思想,把说明∠MPN=180°转化
为说明点M,P,N 在同一条直线上,进而把问题转
化为利用平行线的基本性质说明直线PM 与直线PN
是同一条直线.
总 结
典题精讲
在每一步推理后面的括号内填上理由.
(1)如图①,因为AB∥CD,EF∥CD,所以AB∥EF
(____________________________________).
(2)如图②,因为AB∥CD,过点F 作EF∥AB
(____________________________________________________),
所以EF∥CD (____________________________________).
1
过直线外一点,有且只有一条直线与这条直线平行
平行于同一条直线的两条直线平行
平行于同一条直线的两条直线平行
典题精讲
下列说法中,错误的有( )
①若a 与c 相交,b 与c 相交,则a 与b 相交;
②若a∥b,b∥c,则a∥c;
③过直线外一点有且只有一条直线与已知直线平行;④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个 C.1个 D.0个
2
B
易错提醒
某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,则这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次左拐50°,第二次左拐130°
易错点:混淆两角的位置关系,画不出图形而致错
A
学以致用
小试牛刀
如图,能判定EB∥AC 的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠C=∠EBD
1
D
小试牛刀
下列说法正确的是( )
A.两条不相交的直线叫做平行线
B.过一点有且只有一条直线与已知直线平行
C.在同一平面内不相交的两条线段互相平行
D.在同一平面内不相交的两条直线叫做平行线
D
2
小试牛刀
3
如图,点B 在DC 上,BE 平分∠ABD,∠ABE=∠C,试说
明:BE∥AC.解:因为BE 平分∠ABD,
所以∠ABE=∠DBE
(___________________).
因为∠ABE=∠C,
所以∠DBE=∠C.
所以BE∥AC (____________________________).
角平分线的定义
同位角相等,两直线平行
如图,已知∠1=68°,∠2=68°,∠3=112°.
(1)因为∠1=68°,∠2=68°(已知),
所以∠1=∠2.
所以______∥______(同位角相等,两直线平行).
(2)因为∠3+∠4=180°(平角的定义),∠3=112°,
所以∠4=68°.
又因为∠2=68°,
所以∠2=∠4.
所以______∥_____(同位角相等,两直线平行).
小试牛刀
4
a
b
c
b
小试牛刀
5
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(_______),
所以a∥b (__________________________).
因为∠3=∠4(_________),
所以b∥c (_________________________).
所以a∥c (____________________________________).
已知
同位角相等,两直线平行
平行于同一条直线的两条直线平行
已知
同位角相等,两直线平行
小试牛刀
6
如图,已知∠1=90°,∠2=90°,试说明:CD∥EF.
(1)方法一:用“同位角相等”说明.
(2)方法二:用“第三直线”说明.
小试牛刀
(1)方法一:因为∠1=90°,∠2=90°,
所以∠1=∠2.
所以CD∥EF.
(2)方法二:因为∠1=90°,∠2=90°,
所以CD⊥AB,EF⊥AB.
所以CD∥EF.
解:
小试牛刀
7
在同一平面内,已知A,B,C 是直线l 同旁的三个点.
(1)如果AB∥l,BC∥l,那么A,B,C 三点在同一条直线上
吗?为什么?
(2)如果AB⊥l,BC⊥l,那么A,B,C 三点在同一条直线上
吗?为什么?
小试牛刀
(1)在同一条直线上,因为直线AB,BC 都经过点B,且都与直线 l 平行,而过直线外一点有且只有一条直线与这条直线平行,所以AB,BC 为同一条直线.所以A,B,C 三点在同一条直线上.
(2)在同一条直线上,因为AB,BC 都经过点B,且都与直线 l 垂直,而在同一平面内,过一点有且只有一条直线与已知直线垂直,所以AB,BC 为同一条直线.所以A,B,C 三点在同一条直线上.
解:
小试牛刀
8
如图,∠ABC=∠ACB,BD 平分∠ABC,CE 平分∠ACB,
∠DBF=∠F,问:CE 与DF 的位置关系怎样?试说明理由.
小试牛刀
CE∥DF.理由如下:
因为BD 平分∠ABC,CE 平分∠ACB,
所以∠DBC= ∠ABC,∠BCE= ∠ACB.
因为∠ABC=∠ACB,所以∠DBC=∠BCE.
因为∠DBF=∠F,所以∠BCE=∠F.
所以CE∥DF.
解:
课堂小结
课堂小结
1.平行线的判定方法:
(1)两条直线被另一条直线截得的同位角相等;
(2)两条直线同平行于第三条直线;
(3)在同一平面内,两条直线同垂直于第三条直线.
2.判定两直线平行的方法:
(1)利用平行线的定义判定;
(2)利用“同位角相等,两直线平行”判定;
(3)利用“第三直线”(平行或垂直)判定.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
