【班海精品】北师大版(新)七下-2.2探索直线平行的条件 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-2.2探索直线平行的条件 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:28 | ||
图片预览







文档简介
(共45张PPT)
2.2探索直线平行的条件
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断两直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
新课精讲
探索新知
1
知识点
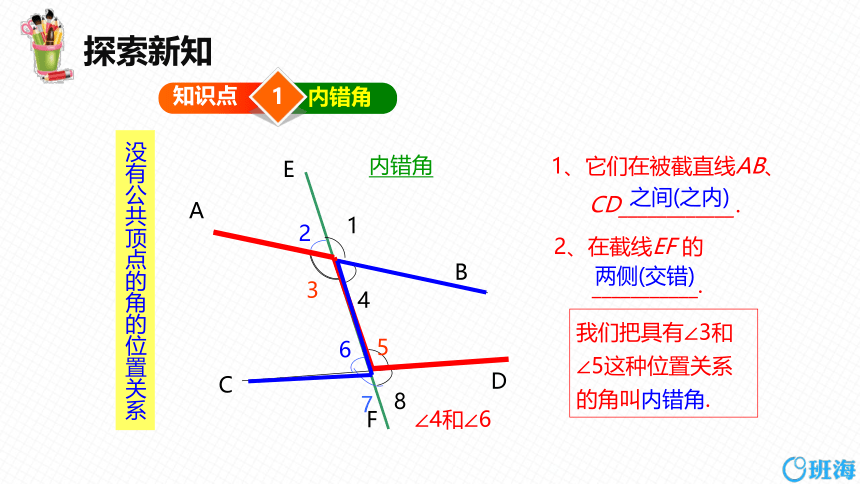
内错角
A
B
C
D
E
F
2
7
6
4
没有公共顶点的角的位置关系
内错角
1、它们在被截直线AB、
CD____________.
2、在截线EF 的
___________.
1
8
3
5
两侧(交错)
我们把具有∠3和∠5这种位置关系的角叫内错角.
∠4和∠6
之间(之内)
探索新知
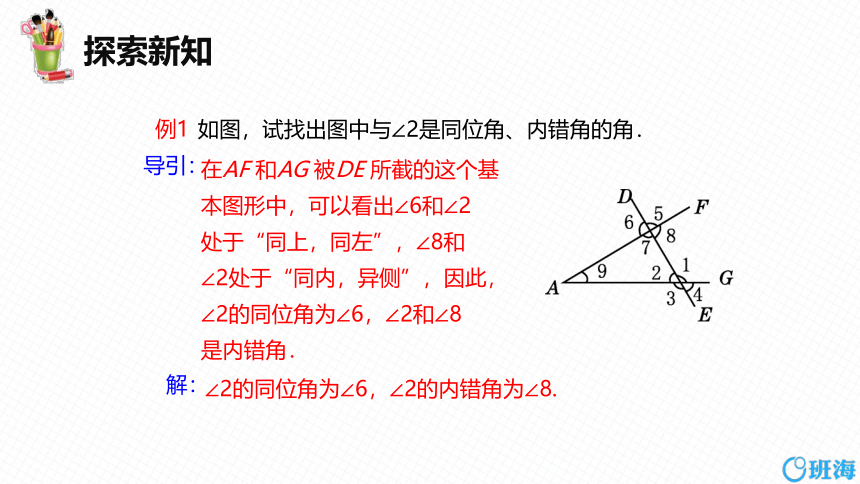
例1
如图,试找出图中与∠2是同位角、内错角的角.
在AF 和AG 被DE 所截的这个基
本图形中,可以看出∠6和∠2
处于“同上,同左”,∠8和
∠2处于“同内,异侧”,因此,
∠2的同位角为∠6,∠2和∠8
是内错角.
导引:
∠2的同位角为∠6,∠2的内错角为∠8.
解:
探索新知
寻找一个角的同位角、内错角,首先应该把这个角放在一个“三线八角”的基本图形中,其次不管是同位角,还是内错角,它们具有一个共同特征,这两个角有一边在同一直线上,这条直线就是定义中的“第三条直线”,而这两个角剩下的两边所在的直线就是两条被截的直线 ;最后看这两个角的位置特征是否满足同位角、内错角的位置特征:三边成“F”“Z”形.
总 结
典题精讲
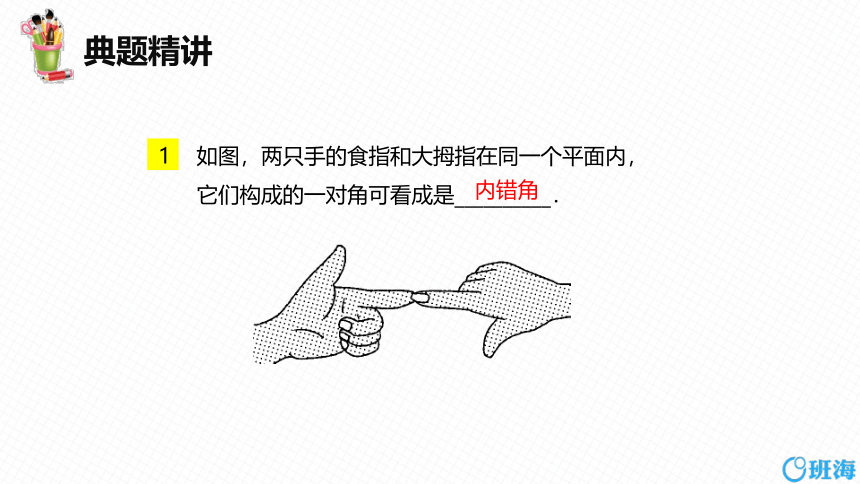
1 如图,两只手的食指和大拇指在同一个平面内,
它们构成的一对角可看成是__________.
内错角
典题精讲
2 在我们常见的英文字母中,也存在着同位角、内错
角、同旁内角,在下面几个字母中,含有内错角最
少的字母是( )
C
探索新知
2
知识点
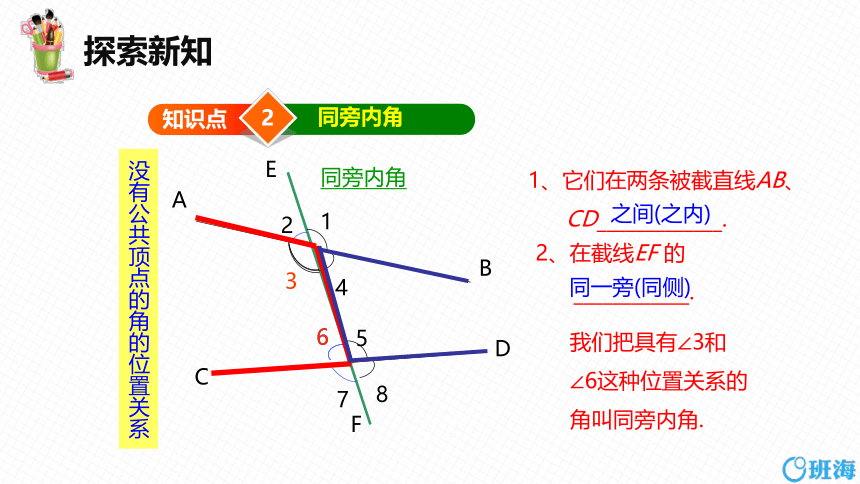
同旁内角
A
B
C
D
E
F
2
7
6
没有公共顶点的角的位置关系
同旁内角
1、它们在两条被截直线AB、
CD_____________.
2、在截线EF 的
____________.
1
8
4
5
3
6
之间(之内)
同一旁(同侧)
我们把具有∠3和∠6这种位置关系的角叫同旁内角.
探索新知
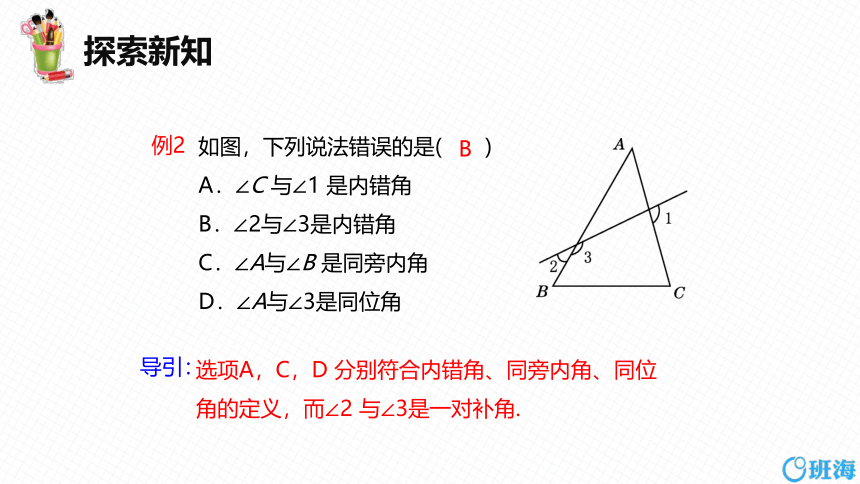
例2
如图,下列说法错误的是( )
A.∠C 与∠1 是内错角
B.∠2与∠3是内错角
C.∠A与∠B 是同旁内角
D.∠A与∠3是同位角
选项A,C,D 分别符合内错角、同旁内角、同位
角的定义,而∠2 与∠3是一对补角.
导引:
B
探索新知
本题运用定义法. 识别同位角、内错角、同旁内角的关键是看两个角所涉及直线是否只有三条,并且有没有一条边在同一直线(截线)上,如果没有,就不是;如果有,再根据角的位置特征判断.
总 结
典题精讲
1 观察右图并填空:
(1)∠1与_______是同位角;
(2)∠5与_______是同旁内角;
(3)∠2与_______是内错角.
∠4
∠3
∠1
典题精讲
2 如图,直线AB,CD 被直线EF 所截,则∠3的同旁内角是( )
A.∠1
B.∠2
C.∠4
D.∠5
B
探索新知
3
知识点
内错角相等,两直线平行
议一议
(1)内错角满足什么关系时,两直线平行?为什么?
探索新知
两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行.
简称为:内错角相等,两直线平行.
归 纳
探索新知
例3
如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
∠AEF 和∠EFC 是直线AB,CD 被直线EF 所截得到
的内错角,根据“内错角相等,两直线平行”可知,
AB∥CD.
导引:
B
探索新知
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两条直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
总 结
典题精讲
下列图形中,由∠1=∠2能得到AB∥CD 的是( )
1
B
典题精讲
如图,在四边形ABCD 中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠4=∠5
2
D
探索新知
4
知识点
同旁内角互补,两直线平行
议一议
(2)同旁内角满足什么关系时,两直线平行?为什么
探索新知
两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
简称为:同旁内角互补,两直线平行.
归 纳
探索新知
判定方法3:两条直线被第三条直线所截,如果同旁内
角互补,那么这两条直线平行;
简称:同旁内角互补,两直线平行.
表达方式:
如图:
因为∠1+∠2=180°(已知),
所以a∥b (同旁内角互补,两直线平行).
探索新知
例4
如图,直线AE,CD 相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
由题意可知
∠1=∠AOD=70°,
又因为∠A=110°,
所以∠A+∠AOD=180°,
故AB∥CD.
导引:
探索新知
因为∠1=∠AOD (对顶角相等),
∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD (同旁内角互补,两直线平行).
解:
典题精讲
当图中各角分别满足下列条件时,你能指出哪两条直线平行吗?
(1)∠1=∠4;
(2)∠2=∠4;
(3)∠1+∠4=180°.
1
(1)a∥b.
(2)m∥l.
(3)l∥n.
解:
典题精讲
如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB 与CD 相交
2
C
典题精讲
如图,直线a,b 被直线c 所截,下列条件不能判定直线a 与b 平行的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠1=∠4
D.∠3=∠4
3
D
易错提醒
如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个 C.3个 D.4个
A
易错点:不能准确识别截线和被截线,从而误判两直线平行.
学以致用
小试牛刀
如图,直线a,b 被c 所截,则∠1与∠2是( )
A.同位角
B.内错角
C.同旁内角
D.邻补角
B
1
小试牛刀
如图,下列推理错误的是( )
A.若∠1=∠2,则c∥d
B.若∠3=∠4,则c∥d
C.若∠1=∠3,则a∥b
D.若∠1=∠4,则a∥b
2
C
小试牛刀
如图,点E 在BC 的延长线上,下列条件中能判定BC∥AD 的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
3
C
小试牛刀
4
如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(_____________).
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF (_________________________).
内错角相等,两直线平行
垂直的定义
小试牛刀
5
将下面的说明过程补充完整.
如图,已知直线NF 与直线AB,CD 分别交于点E,F,直线AM 与直线HB 交于点A,且∠1=∠4=105°,∠2=75°.
试说明:AM∥NF,AB∥CD.
小试牛刀
解:因为∠2=∠3(______________),
∠2=75°(已知),所以∠3=75°.
因为∠1=105°(已知),
所以∠MAB=180°-∠1=75°,
所以∠MAB=∠3.
所以AM∥NF (__________________________).
因为∠3=75°,∠4=105°,
所以∠3+∠4=180°.
所以AB∥CD (____________________________).
对顶角相等
内错角相等,两直线平行
同旁内角互补,两直线平行
小试牛刀
6
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(_______),
所以a∥b (___________________________).
因为∠3+∠4=180°(_______),
所以b∥c (____________________________).
所以a∥c (___________________________________
____________________________).
已知
内错角相等,两直线平行
已知
同旁内角互补,两直线平行
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
小试牛刀
7
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,
∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
小试牛刀
OA∥BC,OB∥AC.理由如下:
因为∠1=50°,∠2=50°,所以∠1=∠2.
所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°.
所以OA∥BC.
解:
小试牛刀
8
如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
如图,过点C 在AC 左侧作∠ACF=∠A,
所以AB∥CF.
又因为∠A+∠ACD+∠D=360°,
所以∠ACF+∠ACD+∠D=360°.
又因为∠ACF+∠ACD+∠DCF=360°,
所以∠DCF=∠D.所以CF∥DE.
所以AB∥DE.
解:
课堂小结
课堂小结
内部同侧
在两条被截直线内部,在截线的同侧
同旁内角
内部异侧
在两条被截直线内部,在截线的异侧(交错)
内错角
位置特征
角的名称
课堂小结
1.由“内错角相等”判定两直线平行:内错角相等,
两直线平行.
2.由“同旁内角”判定两直线平行:同旁内角互补,
两直线平行.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.2探索直线平行的条件
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
判断两直线平行的方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
新课精讲
探索新知
1
知识点
内错角
A
B
C
D
E
F
2
7
6
4
没有公共顶点的角的位置关系
内错角
1、它们在被截直线AB、
CD____________.
2、在截线EF 的
___________.
1
8
3
5
两侧(交错)
我们把具有∠3和∠5这种位置关系的角叫内错角.
∠4和∠6
之间(之内)
探索新知
例1
如图,试找出图中与∠2是同位角、内错角的角.
在AF 和AG 被DE 所截的这个基
本图形中,可以看出∠6和∠2
处于“同上,同左”,∠8和
∠2处于“同内,异侧”,因此,
∠2的同位角为∠6,∠2和∠8
是内错角.
导引:
∠2的同位角为∠6,∠2的内错角为∠8.
解:
探索新知
寻找一个角的同位角、内错角,首先应该把这个角放在一个“三线八角”的基本图形中,其次不管是同位角,还是内错角,它们具有一个共同特征,这两个角有一边在同一直线上,这条直线就是定义中的“第三条直线”,而这两个角剩下的两边所在的直线就是两条被截的直线 ;最后看这两个角的位置特征是否满足同位角、内错角的位置特征:三边成“F”“Z”形.
总 结
典题精讲
1 如图,两只手的食指和大拇指在同一个平面内,
它们构成的一对角可看成是__________.
内错角
典题精讲
2 在我们常见的英文字母中,也存在着同位角、内错
角、同旁内角,在下面几个字母中,含有内错角最
少的字母是( )
C
探索新知
2
知识点
同旁内角
A
B
C
D
E
F
2
7
6
没有公共顶点的角的位置关系
同旁内角
1、它们在两条被截直线AB、
CD_____________.
2、在截线EF 的
____________.
1
8
4
5
3
6
之间(之内)
同一旁(同侧)
我们把具有∠3和∠6这种位置关系的角叫同旁内角.
探索新知
例2
如图,下列说法错误的是( )
A.∠C 与∠1 是内错角
B.∠2与∠3是内错角
C.∠A与∠B 是同旁内角
D.∠A与∠3是同位角
选项A,C,D 分别符合内错角、同旁内角、同位
角的定义,而∠2 与∠3是一对补角.
导引:
B
探索新知
本题运用定义法. 识别同位角、内错角、同旁内角的关键是看两个角所涉及直线是否只有三条,并且有没有一条边在同一直线(截线)上,如果没有,就不是;如果有,再根据角的位置特征判断.
总 结
典题精讲
1 观察右图并填空:
(1)∠1与_______是同位角;
(2)∠5与_______是同旁内角;
(3)∠2与_______是内错角.
∠4
∠3
∠1
典题精讲
2 如图,直线AB,CD 被直线EF 所截,则∠3的同旁内角是( )
A.∠1
B.∠2
C.∠4
D.∠5
B
探索新知
3
知识点
内错角相等,两直线平行
议一议
(1)内错角满足什么关系时,两直线平行?为什么?
探索新知
两条直线被第三条直线所截,如果内错角相等,
那么这两条直线平行.
简称为:内错角相等,两直线平行.
归 纳
探索新知
例3
如图,∠AEF=∠EFC,则下列结论中正确的是( )
A.AD∥BC
B.AB∥CD
C.AD∥EF
D.EF∥BC
∠AEF 和∠EFC 是直线AB,CD 被直线EF 所截得到
的内错角,根据“内错角相等,两直线平行”可知,
AB∥CD.
导引:
B
探索新知
利用内错角相等来判定两直线平行的方法:
(1)看两角是不是两条直线被第三条直线截得的角;
(2)看两角是不是由上述直线形成的内错角,若是,看其是否相等.若相等,则两条直线平行.
总 结
典题精讲
下列图形中,由∠1=∠2能得到AB∥CD 的是( )
1
B
典题精讲
如图,在四边形ABCD 中,连接AC,BD,若要使AB∥CD,则需要添加的条件是( )
A.∠1=∠2
B.∠2=∠3
C.∠3=∠4
D.∠4=∠5
2
D
探索新知
4
知识点
同旁内角互补,两直线平行
议一议
(2)同旁内角满足什么关系时,两直线平行?为什么
探索新知
两条直线被第三条直线所截,如果同旁内角互补,
那么这两条直线平行.
简称为:同旁内角互补,两直线平行.
归 纳
探索新知
判定方法3:两条直线被第三条直线所截,如果同旁内
角互补,那么这两条直线平行;
简称:同旁内角互补,两直线平行.
表达方式:
如图:
因为∠1+∠2=180°(已知),
所以a∥b (同旁内角互补,两直线平行).
探索新知
例4
如图,直线AE,CD 相交于点O,如果∠A=110°,∠1=70°,就可以说明AB∥CD,这是为什么?
由题意可知
∠1=∠AOD=70°,
又因为∠A=110°,
所以∠A+∠AOD=180°,
故AB∥CD.
导引:
探索新知
因为∠1=∠AOD (对顶角相等),
∠1=70°,
所以∠AOD=70°.
又因为∠A=110°,
所以∠A+∠AOD=180°(等式的性质).
所以AB∥CD (同旁内角互补,两直线平行).
解:
典题精讲
当图中各角分别满足下列条件时,你能指出哪两条直线平行吗?
(1)∠1=∠4;
(2)∠2=∠4;
(3)∠1+∠4=180°.
1
(1)a∥b.
(2)m∥l.
(3)l∥n.
解:
典题精讲
如图,工人师傅在工程施工中需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC
B.BC∥CD
C.AB∥DC
D.AB 与CD 相交
2
C
典题精讲
如图,直线a,b 被直线c 所截,下列条件不能判定直线a 与b 平行的是( )
A.∠1=∠3
B.∠2+∠4=180°
C.∠1=∠4
D.∠3=∠4
3
D
易错提醒
如图,下列推理正确的有( )
①因为∠1=∠4,所以BC∥AD;
②因为∠2=∠3,所以AB∥CD;
③因为∠BCD+∠ADC=180°,所以AD∥BC;
④因为∠1+∠2+∠C=180°,所以BC∥AD.
A.1个 B.2个 C.3个 D.4个
A
易错点:不能准确识别截线和被截线,从而误判两直线平行.
学以致用
小试牛刀
如图,直线a,b 被c 所截,则∠1与∠2是( )
A.同位角
B.内错角
C.同旁内角
D.邻补角
B
1
小试牛刀
如图,下列推理错误的是( )
A.若∠1=∠2,则c∥d
B.若∠3=∠4,则c∥d
C.若∠1=∠3,则a∥b
D.若∠1=∠4,则a∥b
2
C
小试牛刀
如图,点E 在BC 的延长线上,下列条件中能判定BC∥AD 的是( )
A.∠1=∠2 B.∠DAB+∠D=180°
C.∠3=∠4 D.∠B=∠DCE
3
C
小试牛刀
4
如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(_____________).
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF (_________________________).
内错角相等,两直线平行
垂直的定义
小试牛刀
5
将下面的说明过程补充完整.
如图,已知直线NF 与直线AB,CD 分别交于点E,F,直线AM 与直线HB 交于点A,且∠1=∠4=105°,∠2=75°.
试说明:AM∥NF,AB∥CD.
小试牛刀
解:因为∠2=∠3(______________),
∠2=75°(已知),所以∠3=75°.
因为∠1=105°(已知),
所以∠MAB=180°-∠1=75°,
所以∠MAB=∠3.
所以AM∥NF (__________________________).
因为∠3=75°,∠4=105°,
所以∠3+∠4=180°.
所以AB∥CD (____________________________).
对顶角相等
内错角相等,两直线平行
同旁内角互补,两直线平行
小试牛刀
6
如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a 与c 平行吗?为什么?
解:a 与c 平行.
理由:因为∠1=∠2(_______),
所以a∥b (___________________________).
因为∠3+∠4=180°(_______),
所以b∥c (____________________________).
所以a∥c (___________________________________
____________________________).
已知
内错角相等,两直线平行
已知
同旁内角互补,两直线平行
如果两条直线都与第三条直线平行,
那么这两条直线也互相平行
小试牛刀
7
如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,
∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
小试牛刀
OA∥BC,OB∥AC.理由如下:
因为∠1=50°,∠2=50°,所以∠1=∠2.
所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°.
所以OA∥BC.
解:
小试牛刀
8
如图,已知∠A+∠ACD+∠D=360°,试说明:AB∥DE.
如图,过点C 在AC 左侧作∠ACF=∠A,
所以AB∥CF.
又因为∠A+∠ACD+∠D=360°,
所以∠ACF+∠ACD+∠D=360°.
又因为∠ACF+∠ACD+∠DCF=360°,
所以∠DCF=∠D.所以CF∥DE.
所以AB∥DE.
解:
课堂小结
课堂小结
内部同侧
在两条被截直线内部,在截线的同侧
同旁内角
内部异侧
在两条被截直线内部,在截线的异侧(交错)
内错角
位置特征
角的名称
课堂小结
1.由“内错角相等”判定两直线平行:内错角相等,
两直线平行.
2.由“同旁内角”判定两直线平行:同旁内角互补,
两直线平行.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
