【班海精品】北师大版(新)七下-3.3用图象表示的变量间关系 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-3.3用图象表示的变量间关系 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
3.3用图象表示的变量间关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
表示变量间的关系的方法有哪些?
复
习
回
顾
新课精讲
探索新知
1
知识点
用折线型图象表示变量间的关系
每一辆汽车上都有一个时速表用来指示汽车当
时的速度. 你知道现在汽车的速度是多少吗?
探索新知
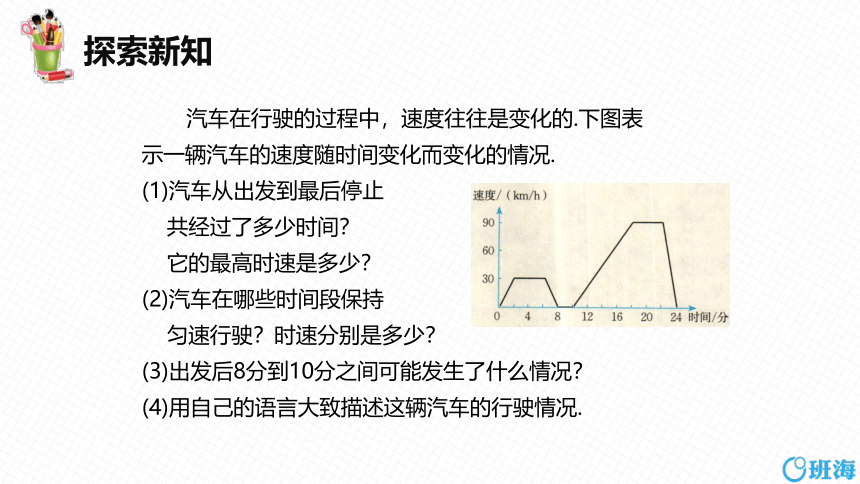
汽车在行驶的过程中,速度往往是变化的.下图表
示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止
共经过了多少时间?
它的最高时速是多少?
(2)汽车在哪些时间段保持
匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
探索新知
定义:在一个变化过程中,两个变量之间的关系不
是一成不变的,有时随着自变量的变化,因变量与
自变量之间的关系也会发生变化,反映在图象上就
是分段图象.
探索新知
例1
下图的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x (min)表示时间,y (km)表示小明离家的距离,小明家、超市、书店在同一条直线上.根据图象回答下列问题.
(1)超市离小明家有多远?
小明走到超市用了多少时间?
(2)超市离书店有多远?小明在
书店购书用了多少时间?
(3)书店离小明家有多远?小明从书店走回家的平均速
度是每分钟多少米?
探索新知
读懂分段图象所表示的实际意义是解决本题的关键.
导引:
解:
(1)由图象可以看出超市离小明家1.1 km,
小明走到超市用了15 min.
(2)超市离书店2-1.1=0.9(km),
小明在书店购书用了55-37=18(min).
(3)由图象可以看出书店离小明家2 km,
小明从书店走回家的平均速度是
探索新知
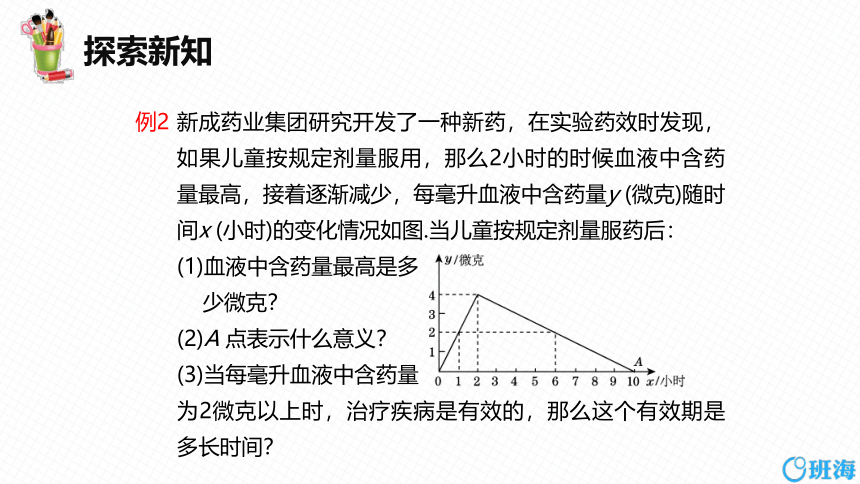
例2
新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2小时的时候血液中含药量最高,接着逐渐减少,每毫升血液中含药量y (微克)随时间x (小时)的变化情况如图.当儿童按规定剂量服药后:
(1)血液中含药量最高是多
少微克?
(2)A 点表示什么意义?
(3)当每毫升血液中含药量
为2微克以上时,治疗疾病是有效的,那么这个有效期是多长时间?
探索新知
(1)由于竖直方向的数轴表示的是因变量(含药量),当
含药量最高时,其在图象中对应的点也为最高,在图
象中找到最高的点,看该点所对应的因变量的取值;
(2)首先在图象中找到A 点的位置,看其对应的自变量
与因变量的值各是多少,结合两个变量的实际意义即
可得到答案;
(3)在图象中可以发现因变量为2对应的点有两个,从
图象中分别确定它们对应的自变量,即可确定有效期
的时间.
导引:
探索新知
(1)血液中含药量最高是4微克;
(2)由于A 点所对应的自变量的值为10,因变量的值
为0,所以A 点表示服药后10小时,血液中含药量
为0微克;
(3)由图象可知,当时间在1小时到6小时之间时,含
药量大于2 微克,所以,有效期的时间为:
6-1=5(小时).
解:
探索新知
运用数形结合思想解答此题.图象上任意一
点都对应了一个自变量的值和一个因变量的值.
总 结
典题精讲
1
小明和哥哥从家里出发去买书,从家出发走了20 min到一个离家1 000 m的书店,小明买了书后随即按原路返回;哥哥看了20 min书后,用15 min返回家.
下面的图象中哪
一个表示哥哥离
家时间与距离之
间的关系( )
D
典题精讲
2 星期六早晨蕊蕊妈妈从家里出发去
观山湖公园锻炼,她连续、匀速走了
60 min后回家,图中的折线段
OA—AB—BC 是她出发后所在位置离家的距离s (km)与行走时间t (min)之间的关系,
则下列图形中可以大致描述蕊蕊妈妈行走的路线的是( )
B
探索新知
2
知识点
从图象中读取变量间关系信息
根据图象读取信息时要把握三个方面:
(1)横轴和纵轴的意义.
(2)对于某个具体点,可向横、纵轴作垂线,从而求得
具体的值;
(3)在实际问题中,要注意图象与横、纵轴的交点代表
的实际意义.
探索新知
例3
某年初,我国西南部分省市遭遇了
严重干旱.某水库的蓄水量随着时
间的增加而减小,干旱持续时间 t
(天)与蓄水量V (万立方米)的变化情
况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t 取0至60天之间的任一值时,对应几个V 值?
(4)写出V 和t 之间的关系式?
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
探索新知
(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表示水库蓄水量,因此它表示的是干旱持
续时间与水库蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)通过分析图象信息可得出.
导引:
探索新知
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
(3)当t 取0至60天之间的任一值时,对应着一个V 值.
(4)根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,
所以V 和t 之间的关系式为
V=1 200- =-20t+1 200(0≤ t ≤60).
解:
干旱持续时间t/天2 0 10 20 30 40 50 60
蓄水量V/万立方米 1 200 1 000 800 600 400 200 0
探索新知
本例通过“形”,即图象中的信息,用列表及关系式这个“数”来表示说明,三种表示方法之间有互补性,是可以相互转化的,体现了数形结合思想的应用.
总 结
探索新知
例4
如图①,在长方形ABCD 中,动点E 从点B 出发,沿
B →A →D →C 方向运动至点C 处停止,设点E 运动的路程为x,三角形BCE 的面积为y,如果y 关于x 的变化关系图象如图②,则当x=7时,点E 应运动到( )
A.点C 处
B.点D 处
C.点B 处
D.点A 处
B
探索新知
x 是自变量,y 是因变量,点E 在运动的过程中,三角形
BCE 的底边BC 不变,而BC 边上的高有时在变化,当点E
在AB 上运动时,BC 边上的高变得越来越大,此时三角形BCE 的面积不断增大;当点E在AD上运动时,BC 边上的
高不变,此时三角形BCE 的面积不变;当点E 在DC 上运
动时,BC 边上的高不断减小,此时三角形BCE 的面积不
断减小.观察图②,可知当x=7时,所对应的点正处于
水平线段与下降线段的交界处,即点E 应运动到面积不发
生变化,若继续运动,面积随着变小的地方.结合图①,
可知点E 运动到了点D 处.
导引:
探索新知
运用数形结合思想来解答,认真观察图形与图象,
仔细分析问题情境中的变量间的变化关系与图象的对
应关系,特别要注意抓住关键点.
总 结
典题精讲
1 如图,折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )
A.4:00气温最低 B.6:00气温为24 ℃
C.14:00气温最高 D.气温是30 ℃的时刻为16:00
D
2 如图是本地区一种产品30天的销售图象,
图①是产品日销售量y (单位:件)与时间t (单位:天)的关
系图,图②是一件产品的销售利润z(单位:元)与时间t
(单位:天)的关系图,已知日销售利润=日销售量×每
件产品的销售利润.下列结论错误的是( )
A.第24天的销售量为200件
B.第20天销售一件产品的
利润是5元
C.第24天与第30天这两天
的日销售利润相等
D.第30天的日销售利润是750元
典题精讲
C
学以致用
小试牛刀
1
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4 s行驶的路程为48 m
B.在0~8 s内甲的速度每秒
增加4 m/s
C.两车到第3 s时行驶的路程相等
D.在4~8 s内甲的速度都大于乙的速度
C
小试牛刀
2
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h 与注水时间t 之间的变化情况的是( )
D
课堂小结
课堂小结
1、通过速度随时间变化的情境,经历从图象中分析
变量之间的过程,加深了对图象表示的理解.
2、不仅读懂了文字语言,而且还读懂图形语言.
3、 最关键是搞清楚自变量、因变量,并且明白了它
们的变化关系.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.3用图象表示的变量间关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
表示变量间的关系的方法有哪些?
复
习
回
顾
新课精讲
探索新知
1
知识点
用折线型图象表示变量间的关系
每一辆汽车上都有一个时速表用来指示汽车当
时的速度. 你知道现在汽车的速度是多少吗?
探索新知
汽车在行驶的过程中,速度往往是变化的.下图表
示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止
共经过了多少时间?
它的最高时速是多少?
(2)汽车在哪些时间段保持
匀速行驶?时速分别是多少?
(3)出发后8分到10分之间可能发生了什么情况?
(4)用自己的语言大致描述这辆汽车的行驶情况.
探索新知
定义:在一个变化过程中,两个变量之间的关系不
是一成不变的,有时随着自变量的变化,因变量与
自变量之间的关系也会发生变化,反映在图象上就
是分段图象.
探索新知
例1
下图的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家.其中x (min)表示时间,y (km)表示小明离家的距离,小明家、超市、书店在同一条直线上.根据图象回答下列问题.
(1)超市离小明家有多远?
小明走到超市用了多少时间?
(2)超市离书店有多远?小明在
书店购书用了多少时间?
(3)书店离小明家有多远?小明从书店走回家的平均速
度是每分钟多少米?
探索新知
读懂分段图象所表示的实际意义是解决本题的关键.
导引:
解:
(1)由图象可以看出超市离小明家1.1 km,
小明走到超市用了15 min.
(2)超市离书店2-1.1=0.9(km),
小明在书店购书用了55-37=18(min).
(3)由图象可以看出书店离小明家2 km,
小明从书店走回家的平均速度是
探索新知
例2
新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2小时的时候血液中含药量最高,接着逐渐减少,每毫升血液中含药量y (微克)随时间x (小时)的变化情况如图.当儿童按规定剂量服药后:
(1)血液中含药量最高是多
少微克?
(2)A 点表示什么意义?
(3)当每毫升血液中含药量
为2微克以上时,治疗疾病是有效的,那么这个有效期是多长时间?
探索新知
(1)由于竖直方向的数轴表示的是因变量(含药量),当
含药量最高时,其在图象中对应的点也为最高,在图
象中找到最高的点,看该点所对应的因变量的取值;
(2)首先在图象中找到A 点的位置,看其对应的自变量
与因变量的值各是多少,结合两个变量的实际意义即
可得到答案;
(3)在图象中可以发现因变量为2对应的点有两个,从
图象中分别确定它们对应的自变量,即可确定有效期
的时间.
导引:
探索新知
(1)血液中含药量最高是4微克;
(2)由于A 点所对应的自变量的值为10,因变量的值
为0,所以A 点表示服药后10小时,血液中含药量
为0微克;
(3)由图象可知,当时间在1小时到6小时之间时,含
药量大于2 微克,所以,有效期的时间为:
6-1=5(小时).
解:
探索新知
运用数形结合思想解答此题.图象上任意一
点都对应了一个自变量的值和一个因变量的值.
总 结
典题精讲
1
小明和哥哥从家里出发去买书,从家出发走了20 min到一个离家1 000 m的书店,小明买了书后随即按原路返回;哥哥看了20 min书后,用15 min返回家.
下面的图象中哪
一个表示哥哥离
家时间与距离之
间的关系( )
D
典题精讲
2 星期六早晨蕊蕊妈妈从家里出发去
观山湖公园锻炼,她连续、匀速走了
60 min后回家,图中的折线段
OA—AB—BC 是她出发后所在位置离家的距离s (km)与行走时间t (min)之间的关系,
则下列图形中可以大致描述蕊蕊妈妈行走的路线的是( )
B
探索新知
2
知识点
从图象中读取变量间关系信息
根据图象读取信息时要把握三个方面:
(1)横轴和纵轴的意义.
(2)对于某个具体点,可向横、纵轴作垂线,从而求得
具体的值;
(3)在实际问题中,要注意图象与横、纵轴的交点代表
的实际意义.
探索新知
例3
某年初,我国西南部分省市遭遇了
严重干旱.某水库的蓄水量随着时
间的增加而减小,干旱持续时间 t
(天)与蓄水量V (万立方米)的变化情
况如图,根据图象回答问题:
(1)这个图象反映了哪两个变量之间的关系?
(2)根据图象填表:
(3)当t 取0至60天之间的任一值时,对应几个V 值?
(4)写出V 和t 之间的关系式?
干旱持续时间t/天 0 10 20 30 40 50 60
蓄水量V/万立方米
探索新知
(1)通过读图可知,横坐标表示干旱持续时间,纵坐标表示水库蓄水量,因此它表示的是干旱持
续时间与水库蓄水量之间的关系;
(2)根据图象信息确定每个特殊点的坐标即可;
(3)观察图象可得;
(4)通过分析图象信息可得出.
导引:
探索新知
(1)图象反映了干旱持续时间与水库蓄水量之间的关系.
(2)填表如下:
(3)当t 取0至60天之间的任一值时,对应着一个V 值.
(4)根据图象可知,该水库初始蓄水量为1 200万立方米,
干旱每持续10天,蓄水量相应减少200万立方米,
所以V 和t 之间的关系式为
V=1 200- =-20t+1 200(0≤ t ≤60).
解:
干旱持续时间t/天2 0 10 20 30 40 50 60
蓄水量V/万立方米 1 200 1 000 800 600 400 200 0
探索新知
本例通过“形”,即图象中的信息,用列表及关系式这个“数”来表示说明,三种表示方法之间有互补性,是可以相互转化的,体现了数形结合思想的应用.
总 结
探索新知
例4
如图①,在长方形ABCD 中,动点E 从点B 出发,沿
B →A →D →C 方向运动至点C 处停止,设点E 运动的路程为x,三角形BCE 的面积为y,如果y 关于x 的变化关系图象如图②,则当x=7时,点E 应运动到( )
A.点C 处
B.点D 处
C.点B 处
D.点A 处
B
探索新知
x 是自变量,y 是因变量,点E 在运动的过程中,三角形
BCE 的底边BC 不变,而BC 边上的高有时在变化,当点E
在AB 上运动时,BC 边上的高变得越来越大,此时三角形BCE 的面积不断增大;当点E在AD上运动时,BC 边上的
高不变,此时三角形BCE 的面积不变;当点E 在DC 上运
动时,BC 边上的高不断减小,此时三角形BCE 的面积不
断减小.观察图②,可知当x=7时,所对应的点正处于
水平线段与下降线段的交界处,即点E 应运动到面积不发
生变化,若继续运动,面积随着变小的地方.结合图①,
可知点E 运动到了点D 处.
导引:
探索新知
运用数形结合思想来解答,认真观察图形与图象,
仔细分析问题情境中的变量间的变化关系与图象的对
应关系,特别要注意抓住关键点.
总 结
典题精讲
1 如图,折线图描述了某地某日的气温变化情况,根据图中信息,下列说法错误的是( )
A.4:00气温最低 B.6:00气温为24 ℃
C.14:00气温最高 D.气温是30 ℃的时刻为16:00
D
2 如图是本地区一种产品30天的销售图象,
图①是产品日销售量y (单位:件)与时间t (单位:天)的关
系图,图②是一件产品的销售利润z(单位:元)与时间t
(单位:天)的关系图,已知日销售利润=日销售量×每
件产品的销售利润.下列结论错误的是( )
A.第24天的销售量为200件
B.第20天销售一件产品的
利润是5元
C.第24天与第30天这两天
的日销售利润相等
D.第30天的日销售利润是750元
典题精讲
C
学以致用
小试牛刀
1
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4 s行驶的路程为48 m
B.在0~8 s内甲的速度每秒
增加4 m/s
C.两车到第3 s时行驶的路程相等
D.在4~8 s内甲的速度都大于乙的速度
C
小试牛刀
2
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h 与注水时间t 之间的变化情况的是( )
D
课堂小结
课堂小结
1、通过速度随时间变化的情境,经历从图象中分析
变量之间的过程,加深了对图象表示的理解.
2、不仅读懂了文字语言,而且还读懂图形语言.
3、 最关键是搞清楚自变量、因变量,并且明白了它
们的变化关系.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
