【班海精品】北师大版(新)七下-3.2用关系式表示的变量间关系【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-3.2用关系式表示的变量间关系【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
3.2用关系式表示的变量的关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
变量与常量的意义是什么?
什么是自变量、因变量?
复
习
回
顾
新课精讲
探索新知
1
知识点
用关系式表示的变量间的关系
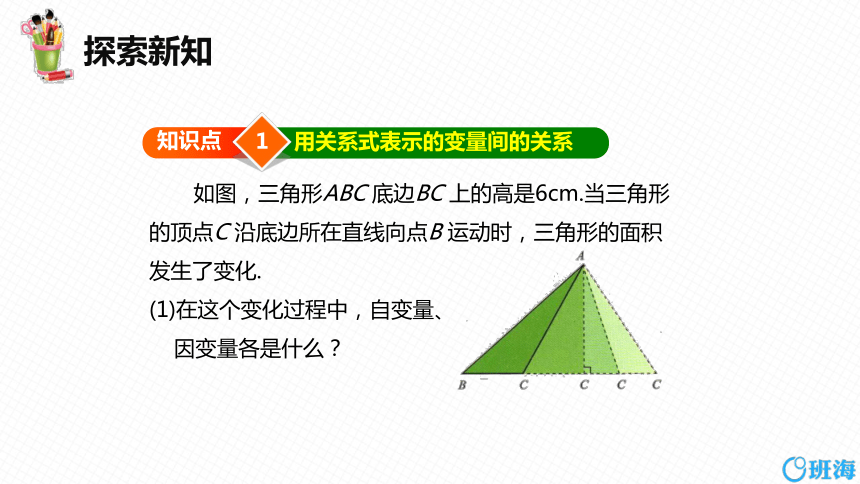
如图,三角形ABC 底边BC 上的高是6cm.当三角形
的顶点C 沿底边所在直线向点B 运动时,三角形的面积
发生了变化.
(1)在这个变化过程中,自变量、
因变量各是什么?
探索新知
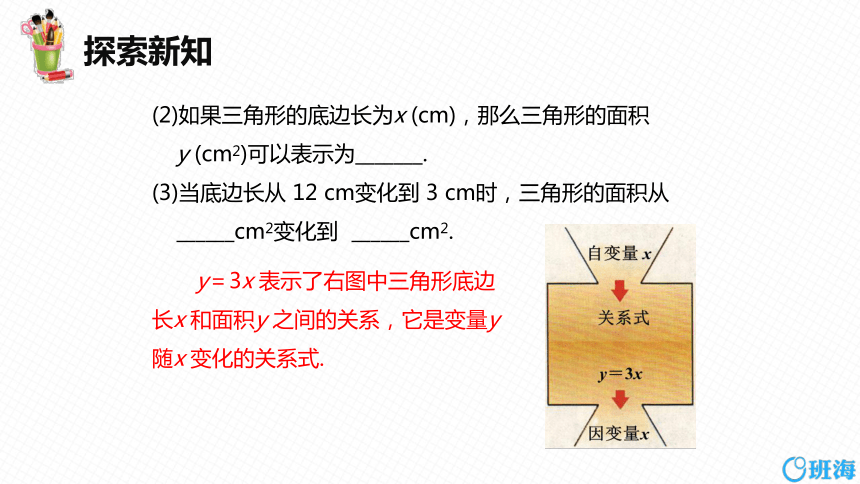
(2)如果三角形的底边长为x (cm),那么三角形的面积
y (cm2)可以表示为_______.
(3)当底边长从 12 cm变化到 3 cm时,三角形的面积从
______cm2变化到 ______cm2.
y=3x 表示了右图中三角形底边
长x 和面积y 之间的关系,它是变量y
随x 变化的关系式.
探索新知
关系式是我们表示变量之间关系的另一种方法.利
用关系式(如y=3x ),我们可以根据任何一个自变量的
值求出相应的因变量的值.
归 纳
做一做
如图,圆锥的高是4cm,当圆
锥的底面半径由小到大变化时,
圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、
因变量各是什么?
(2)如果圆锥底面半径为r (cm),那么圆锥的体积V (cm3)
与r 的关系式为________.
(3)当底面半径由1cm变化到10cm时,圆锥的体积由
________cm3变化到________cm3.
探索新知
探索新知
用来表示自变量和因变量之间关系的
等式叫做关系式.
探索新知
例1
长方形的周长为24 cm,其中一边长为x cm(x>0),面积为y cm2,则该长方形中y 与x 的关系可以写为( )
A.y=x 2 B.y=(12-x )2
C.y=(12-x )·x D.y=2(12-x )
因为长方形的周长为24 cm,其中一边长为x cm,
所以另一边长为(12-x ) cm,因为面积为y cm2,
所以该长方形中y 与x 的关系可以写为y=(12-x )·x.
导引:
C
探索新知
解决此类问题时,关键是要运用建模思想,先分
析题意,用两个不同的字母分别表示出两个变量,如
此题中用x 表示自变量,用y 表示因变量,然后根据问
题中所蕴含的等量关系列出等式,最后将等式转化为
用含自变量的代数式表示因变量的形式.
总 结
探索新知
例2
百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其销售量x (米)与售价y (元)如下表:
下列用销售量x (米)表示售价y (元)的关系式中,正确的是
( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
通过观察表格内x 与y 的关系,可知y 的值相对于x=1时是
成倍增长的,由此可得y=(8+0.3)x.
导引:
销售量x/米 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
B
探索新知
从表格中能直接得到自变量与因变量具体的对应
值,根据这些值能够归纳出两个变量之间的变化规律.
总 结
典题精讲
1
2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和2015年我省财政收入分别为a 亿元和b 亿元,则a,b 之间满足的关系式为( )
A.b=a (1+8.9%+9.5%)
B.b=a (1+8.9%×9.5%)
C.b=a (1+8.9%)(1+9.5%)
D.b=a (1+8.9%)2(1+9.5%)
C
典题精讲
2 某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了 .如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y 与x 之间的关系式和自变量取值范围分别是( )
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤ x ≤500
D.y=60-0.12x,0≤ x ≤500
D
下列用长度x 表示售价y 的关系式中,正确的是( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
典题精讲
3
百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x 与售价y 如下表:
B
长度x/m 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
探索新知
2
知识点
用关系式求值
议一议
你知道什么是“低碳生活”吗? “低碳生活”
是指人们生活中尽量减少所耗能量,从而降低碳(特
别是二氧化碳)的排放量的一种生活方式.
探索新知
(1)用字母表示家居用电的二氧
化碳排放量的公式为_____,
其中的字母表示_______.
(2)在上述关系式中,耗电量每
增加1 kW·h (kW·h是单位
“千瓦时”的符号),二氧化
碳排放量增加________.
当耗电量从1 kW·h增加到100 kW·h时,二氧化碳排放量
从________增加到________.
(3)小明家本月用电大约110 kW·h、天然气20 m3、自来水5 t、
耗油 75 L,请你计算一下小明家这几项的二氧化碳排放量.
探索新知
例3
某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y (万元)与年数x 之间的关系式为 __________;
(2)5年后的年产值是______万元.
(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x 年后增加2x 万元,所以年产值
y (万元)与年数x 之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
导引:
y=2x+15
25
探索新知
用变量之间的关系式来解决实际问题,主要分两
步来进行:第一步是根据实际问题里的等量关系列出
关系式,这一步是关键;第二步是利用关系式来解决
实际问题,其基本思路是将自变量(或因变量)的值代入
关系式中求值,如此题中,将x=5代入关系式中求得
y=25,即求得5年后的年产值为25万元.
总 结
探索新知
例4
观察图,回答问题.
(1)设图形的周长为L,梯形的个数为n,试写出L 与
n 之间的关系式;
(2)n=11时图形的周长是多少?
导引:
(1)由图可知,每增加一个梯形,就增加一个上底、
下底的和,据此可得L 与n 之间的关系式;
(2)将数值代入关系式即可求解.
探索新知
解:
(1)根据图形分析可得梯形的个数增加1个,周长L 增加3.
故L 与n 之间的关系式为
L=5+(n-1)×3=5+3n-3=3n+2.
(2)n=11时,代入关系式得L=3×11+2=35.
典题精讲
1
在地球某地,温度T (℃)与高度d (m)的关系可以近似地用T=10- 来表示. 根据这个关系式,当d 的值分别是0,200,400,600,800,1 000时,计算相应的T 值,并用表格表示所得结果.
解:用表格表示所得结果如下:
高度d/m 0 200 400 600 800 1000
温度T/℃ 10.0 8.7 7.3 6.0 4.7 3.3
典题精讲
2
仿照“议一议”中的(2),你能说一说家用自来水二氧化碳排放量随自来水使用吨数的变化而变化的情况吗?
自来水使用量每增加1 t,二氧化碳排放量增加0.91 kg.当自来水使用量从1 t增加到10 t时,二氧化碳排放量从0.91 kg增加到9.1 kg.
解:
典题精讲
3 变量y 与x 之间的关系式是y= x 2+1,当自变量x
=2时,因变量y 的值是( )
A.-2 B.-1 C.1 D.3
4 某地海拔高度h 与温度T 的关系可用T=21-6h 来表示
(其中温度单位为℃,海拔高度单位为km),则该地区某海拔高度为2 000 m的山顶上的温度为( )
A.15 ℃ B.9 ℃ C.3 ℃ D.7 ℃
D
B
典题精讲
5 一个长方体的体积为12 cm3,当底面积不变,高
增大时,长方体的体积发生变化,若底面积不变,
高变为原来的3倍,则体积变为( )
A.12 cm3 B.24 cm3
C.36 cm3 D.48 cm3
C
易错提醒
有一种粗细均匀的电线,为了确定其长度,从一捆上剪下1 m,称得它的质量是0.06 kg.
(1)写出这种电线长度与质量之间的关系式;
(2)如果一捆电线剪下1 m后的质量为b kg,请写出这捆电线的总长度.
易错点:混淆自变量与因变量导致关系式错误
(1)设电线的长度为l m,质量为m kg,则有l= .
(2)设这捆电线的总长度为L m,则L= +1,即这捆电线的总长度为 m.
解:
学以致用
小试牛刀
如图,下列各三角形中的三个数字之间均具有相同的规律,根据此规律,最后一个三角形中y 与n 之间的关系是( )
B
A.y=2n+1 B.y=2n+n
C.y=2n+1+n D.y=2n+n+1
1
小试牛刀
2 已知三角形ABC 的底边BC 上的高为8 cm,当底
边BC 从16 cm变化到5 cm时,三角形ABC 的面
积( )
A.从20 cm2变化到64 cm2
B.从64 cm2变化到20 cm2
C.从128 cm2变化到40 cm2
D.从40 cm2变化到128 cm2
B
小试牛刀
3
某市出租车车费标准如下:3 km以内(含3 km)收费8元;
超过3 km的部分每千米收费1.6元.
(1)写出应收费y (元)与出租车行驶路程x (km)之间的关系式
(其中x ≥3).
(2)小亮乘出租车行驶4 km,应付车费多少元?
(3)小波付车费16元,那么出租车行驶了多少千米?
小试牛刀
(1)根据题意,可得
y=8+(x-3)×1.6,
所以y=1.6x+3.2(x ≥3).
(2)当x=4时,y=1.6x+3.2=1.6×4+3.2=9.6.
答:应付车费9.6元.
(3)当y=16时,16=1.6x+3.2,
解得x=8.
答:出租车行驶了8 km.
解:
小试牛刀
4
如图,平行四边形ABCD 的底边BC上的高为6 cm,当边
DC 向右平移时,平行四边形的面积发生了变化.
(1)在这个变化过程中,自变量,因变量各是什么?
(2)如果底边BC 的长为x (cm),那么平行四边形的面积
y (cm2)可以表示为______________.
(3)当底边BC 的长从12 cm增加到20 cm时,平行四边形
ABCD 的面积增加了多少?
y=6x (x >0)
小试牛刀
(1)底边BC 的长是自变量,平行四边形的面积是因变量.
(3)当x=12时,y=6×12=72;
当x=20时,y=6×20=120.
所以平行四边形ABCD 的面积增加了120-72=48(cm2).
解:
小试牛刀
5
如图,自行车每节链条的长度为2.5 cm,交叉重叠部分
的圆的直径为0.8 cm.
(1)观察图形,填写下表:
链条的节数/节 2 3 4 …
链条的长度/cm …
4.2
5.9
7.6
小试牛刀
(2)如果x 节链条的长度为y cm,那么y 与x 之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
(2)y=2.5+(2.5-0.8)(x-1),即y=1.7x+0.8.
(3)当x=60时,y=1.7×60+0.8=102.8.
102.8-0.8=102(cm).
所以这辆自行车上的链条(安装后)总长度为102 cm.
解:
小试牛刀
6
某超市为方便顾客购买,将瓜子放入包装袋内出售,其质量x (kg)与售价y (元)之间的关系如下表(售价中的0.10元是包装袋的费用):
(1)观察表格,写出y 与x 之
间的关系式.
(2)买8 kg这种瓜子需花费
多少元?
(3)用100元去买这种瓜子,最多能买多少千克?
质量x/kg 售价y/元
1 15.00+0.10
2 30.00+0.10
3 45.00+0.10
4 60.00+0.10
…… ……
小试牛刀
(1)y=15x+0.1.
(2)当x=8时,y=15×8+0.1=120.1. 所以买8 kg这种瓜子需花费120.1元.
(3)当y=100时,15x+0.1=100,x=6.66.
所以用100元去买这种瓜子,最多能买6.66 kg.
解:
课堂小结
课堂小结
用关系式表示变量间的关系要明确“三点”:
(1)关系式是用含自变量的代数式表示因变量的等式.
(2)利用关系式表示变量之间的关系,最大的优点在于能比较
方便地求出自变量为取值范围内的任意一个值时,相对应
的因变量的值.利用表格表示变量之间的关系时,对于表
格中没有给出的对应值,在需要时往往只能估计,很难达
到足够的精确度,使用关系式则没有这样的缺点.
(3)利用关系式求因变量的值,实际上就是求代数式的值.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.2用关系式表示的变量的关系
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
变量与常量的意义是什么?
什么是自变量、因变量?
复
习
回
顾
新课精讲
探索新知
1
知识点
用关系式表示的变量间的关系
如图,三角形ABC 底边BC 上的高是6cm.当三角形
的顶点C 沿底边所在直线向点B 运动时,三角形的面积
发生了变化.
(1)在这个变化过程中,自变量、
因变量各是什么?
探索新知
(2)如果三角形的底边长为x (cm),那么三角形的面积
y (cm2)可以表示为_______.
(3)当底边长从 12 cm变化到 3 cm时,三角形的面积从
______cm2变化到 ______cm2.
y=3x 表示了右图中三角形底边
长x 和面积y 之间的关系,它是变量y
随x 变化的关系式.
探索新知
关系式是我们表示变量之间关系的另一种方法.利
用关系式(如y=3x ),我们可以根据任何一个自变量的
值求出相应的因变量的值.
归 纳
做一做
如图,圆锥的高是4cm,当圆
锥的底面半径由小到大变化时,
圆锥的体积也随之发生了变化.
(1)在这个变化过程中,自变量、
因变量各是什么?
(2)如果圆锥底面半径为r (cm),那么圆锥的体积V (cm3)
与r 的关系式为________.
(3)当底面半径由1cm变化到10cm时,圆锥的体积由
________cm3变化到________cm3.
探索新知
探索新知
用来表示自变量和因变量之间关系的
等式叫做关系式.
探索新知
例1
长方形的周长为24 cm,其中一边长为x cm(x>0),面积为y cm2,则该长方形中y 与x 的关系可以写为( )
A.y=x 2 B.y=(12-x )2
C.y=(12-x )·x D.y=2(12-x )
因为长方形的周长为24 cm,其中一边长为x cm,
所以另一边长为(12-x ) cm,因为面积为y cm2,
所以该长方形中y 与x 的关系可以写为y=(12-x )·x.
导引:
C
探索新知
解决此类问题时,关键是要运用建模思想,先分
析题意,用两个不同的字母分别表示出两个变量,如
此题中用x 表示自变量,用y 表示因变量,然后根据问
题中所蕴含的等量关系列出等式,最后将等式转化为
用含自变量的代数式表示因变量的形式.
总 结
探索新知
例2
百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其销售量x (米)与售价y (元)如下表:
下列用销售量x (米)表示售价y (元)的关系式中,正确的是
( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
通过观察表格内x 与y 的关系,可知y 的值相对于x=1时是
成倍增长的,由此可得y=(8+0.3)x.
导引:
销售量x/米 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
B
探索新知
从表格中能直接得到自变量与因变量具体的对应
值,根据这些值能够归纳出两个变量之间的变化规律.
总 结
典题精讲
1
2014年我省财政收入比2013年增长8.9%,2015年比2014年增长9.5%,若2013年和2015年我省财政收入分别为a 亿元和b 亿元,则a,b 之间满足的关系式为( )
A.b=a (1+8.9%+9.5%)
B.b=a (1+8.9%×9.5%)
C.b=a (1+8.9%)(1+9.5%)
D.b=a (1+8.9%)2(1+9.5%)
C
典题精讲
2 某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了 .如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y 与x 之间的关系式和自变量取值范围分别是( )
A.y=0.12x,x>0
B.y=60-0.12x,x>0
C.y=0.12x,0≤ x ≤500
D.y=60-0.12x,0≤ x ≤500
D
下列用长度x 表示售价y 的关系式中,正确的是( )
A.y=8x+0.3 B.y=(8+0.3)x
C.y=8+0.3x D.y=8+0.3+x
典题精讲
3
百货大楼进了一批花布,出售时要在进价(进货价格)的基础上加一定的利润,其长度x 与售价y 如下表:
B
长度x/m 1 2 3 4 …
售价y/元 8+0.3 16+0.6 24+0.9 32+1.2 …
探索新知
2
知识点
用关系式求值
议一议
你知道什么是“低碳生活”吗? “低碳生活”
是指人们生活中尽量减少所耗能量,从而降低碳(特
别是二氧化碳)的排放量的一种生活方式.
探索新知
(1)用字母表示家居用电的二氧
化碳排放量的公式为_____,
其中的字母表示_______.
(2)在上述关系式中,耗电量每
增加1 kW·h (kW·h是单位
“千瓦时”的符号),二氧化
碳排放量增加________.
当耗电量从1 kW·h增加到100 kW·h时,二氧化碳排放量
从________增加到________.
(3)小明家本月用电大约110 kW·h、天然气20 m3、自来水5 t、
耗油 75 L,请你计算一下小明家这几项的二氧化碳排放量.
探索新知
例3
某工厂现在年产值是15万元,计划今后每年增加2万元.
(1)年产值y (万元)与年数x 之间的关系式为 __________;
(2)5年后的年产值是______万元.
(1)根据题意可知,现在年产值是15万元,计划今后
每年增加2万元,x 年后增加2x 万元,所以年产值
y (万元)与年数x 之间的关系式为y=2x+15;
(2)将x=5代入关系式得:y=2x+15=2×5+15=25.
导引:
y=2x+15
25
探索新知
用变量之间的关系式来解决实际问题,主要分两
步来进行:第一步是根据实际问题里的等量关系列出
关系式,这一步是关键;第二步是利用关系式来解决
实际问题,其基本思路是将自变量(或因变量)的值代入
关系式中求值,如此题中,将x=5代入关系式中求得
y=25,即求得5年后的年产值为25万元.
总 结
探索新知
例4
观察图,回答问题.
(1)设图形的周长为L,梯形的个数为n,试写出L 与
n 之间的关系式;
(2)n=11时图形的周长是多少?
导引:
(1)由图可知,每增加一个梯形,就增加一个上底、
下底的和,据此可得L 与n 之间的关系式;
(2)将数值代入关系式即可求解.
探索新知
解:
(1)根据图形分析可得梯形的个数增加1个,周长L 增加3.
故L 与n 之间的关系式为
L=5+(n-1)×3=5+3n-3=3n+2.
(2)n=11时,代入关系式得L=3×11+2=35.
典题精讲
1
在地球某地,温度T (℃)与高度d (m)的关系可以近似地用T=10- 来表示. 根据这个关系式,当d 的值分别是0,200,400,600,800,1 000时,计算相应的T 值,并用表格表示所得结果.
解:用表格表示所得结果如下:
高度d/m 0 200 400 600 800 1000
温度T/℃ 10.0 8.7 7.3 6.0 4.7 3.3
典题精讲
2
仿照“议一议”中的(2),你能说一说家用自来水二氧化碳排放量随自来水使用吨数的变化而变化的情况吗?
自来水使用量每增加1 t,二氧化碳排放量增加0.91 kg.当自来水使用量从1 t增加到10 t时,二氧化碳排放量从0.91 kg增加到9.1 kg.
解:
典题精讲
3 变量y 与x 之间的关系式是y= x 2+1,当自变量x
=2时,因变量y 的值是( )
A.-2 B.-1 C.1 D.3
4 某地海拔高度h 与温度T 的关系可用T=21-6h 来表示
(其中温度单位为℃,海拔高度单位为km),则该地区某海拔高度为2 000 m的山顶上的温度为( )
A.15 ℃ B.9 ℃ C.3 ℃ D.7 ℃
D
B
典题精讲
5 一个长方体的体积为12 cm3,当底面积不变,高
增大时,长方体的体积发生变化,若底面积不变,
高变为原来的3倍,则体积变为( )
A.12 cm3 B.24 cm3
C.36 cm3 D.48 cm3
C
易错提醒
有一种粗细均匀的电线,为了确定其长度,从一捆上剪下1 m,称得它的质量是0.06 kg.
(1)写出这种电线长度与质量之间的关系式;
(2)如果一捆电线剪下1 m后的质量为b kg,请写出这捆电线的总长度.
易错点:混淆自变量与因变量导致关系式错误
(1)设电线的长度为l m,质量为m kg,则有l= .
(2)设这捆电线的总长度为L m,则L= +1,即这捆电线的总长度为 m.
解:
学以致用
小试牛刀
如图,下列各三角形中的三个数字之间均具有相同的规律,根据此规律,最后一个三角形中y 与n 之间的关系是( )
B
A.y=2n+1 B.y=2n+n
C.y=2n+1+n D.y=2n+n+1
1
小试牛刀
2 已知三角形ABC 的底边BC 上的高为8 cm,当底
边BC 从16 cm变化到5 cm时,三角形ABC 的面
积( )
A.从20 cm2变化到64 cm2
B.从64 cm2变化到20 cm2
C.从128 cm2变化到40 cm2
D.从40 cm2变化到128 cm2
B
小试牛刀
3
某市出租车车费标准如下:3 km以内(含3 km)收费8元;
超过3 km的部分每千米收费1.6元.
(1)写出应收费y (元)与出租车行驶路程x (km)之间的关系式
(其中x ≥3).
(2)小亮乘出租车行驶4 km,应付车费多少元?
(3)小波付车费16元,那么出租车行驶了多少千米?
小试牛刀
(1)根据题意,可得
y=8+(x-3)×1.6,
所以y=1.6x+3.2(x ≥3).
(2)当x=4时,y=1.6x+3.2=1.6×4+3.2=9.6.
答:应付车费9.6元.
(3)当y=16时,16=1.6x+3.2,
解得x=8.
答:出租车行驶了8 km.
解:
小试牛刀
4
如图,平行四边形ABCD 的底边BC上的高为6 cm,当边
DC 向右平移时,平行四边形的面积发生了变化.
(1)在这个变化过程中,自变量,因变量各是什么?
(2)如果底边BC 的长为x (cm),那么平行四边形的面积
y (cm2)可以表示为______________.
(3)当底边BC 的长从12 cm增加到20 cm时,平行四边形
ABCD 的面积增加了多少?
y=6x (x >0)
小试牛刀
(1)底边BC 的长是自变量,平行四边形的面积是因变量.
(3)当x=12时,y=6×12=72;
当x=20时,y=6×20=120.
所以平行四边形ABCD 的面积增加了120-72=48(cm2).
解:
小试牛刀
5
如图,自行车每节链条的长度为2.5 cm,交叉重叠部分
的圆的直径为0.8 cm.
(1)观察图形,填写下表:
链条的节数/节 2 3 4 …
链条的长度/cm …
4.2
5.9
7.6
小试牛刀
(2)如果x 节链条的长度为y cm,那么y 与x 之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?
(2)y=2.5+(2.5-0.8)(x-1),即y=1.7x+0.8.
(3)当x=60时,y=1.7×60+0.8=102.8.
102.8-0.8=102(cm).
所以这辆自行车上的链条(安装后)总长度为102 cm.
解:
小试牛刀
6
某超市为方便顾客购买,将瓜子放入包装袋内出售,其质量x (kg)与售价y (元)之间的关系如下表(售价中的0.10元是包装袋的费用):
(1)观察表格,写出y 与x 之
间的关系式.
(2)买8 kg这种瓜子需花费
多少元?
(3)用100元去买这种瓜子,最多能买多少千克?
质量x/kg 售价y/元
1 15.00+0.10
2 30.00+0.10
3 45.00+0.10
4 60.00+0.10
…… ……
小试牛刀
(1)y=15x+0.1.
(2)当x=8时,y=15×8+0.1=120.1. 所以买8 kg这种瓜子需花费120.1元.
(3)当y=100时,15x+0.1=100,x=6.66.
所以用100元去买这种瓜子,最多能买6.66 kg.
解:
课堂小结
课堂小结
用关系式表示变量间的关系要明确“三点”:
(1)关系式是用含自变量的代数式表示因变量的等式.
(2)利用关系式表示变量之间的关系,最大的优点在于能比较
方便地求出自变量为取值范围内的任意一个值时,相对应
的因变量的值.利用表格表示变量之间的关系时,对于表
格中没有给出的对应值,在需要时往往只能估计,很难达
到足够的精确度,使用关系式则没有这样的缺点.
(3)利用关系式求因变量的值,实际上就是求代数式的值.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
