【班海精品】北师大版(新)七下-4.1认识三角形 第四课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-4.1认识三角形 第四课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:28 | ||
图片预览







文档简介
(共41张PPT)
4.1认识三角形
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么是三角形的中线?什么是三角形的角平分线?
2.三角形的三条中线、角平分线相交于一点吗?
这一交点在三角形的内部还是外部?
复
习
回
顾
新课精讲
探索新知
知识点
三角形的高
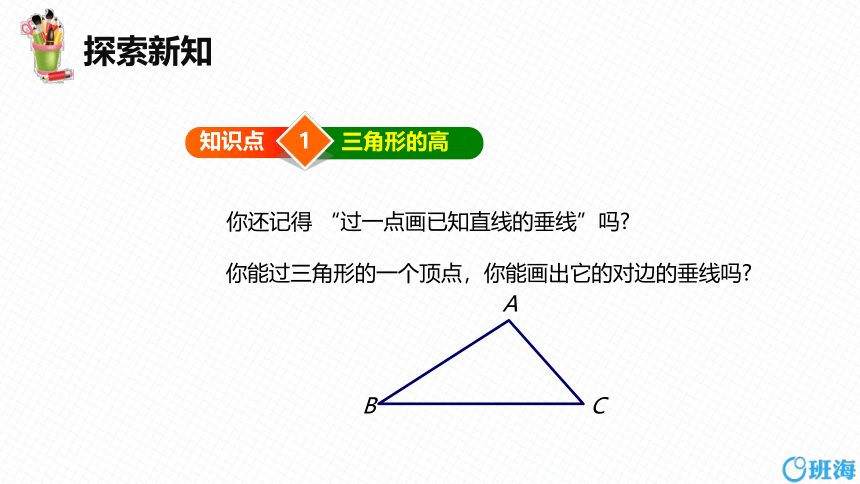
你能过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
你还记得 “过一点画已知直线的垂线”吗
1
探索新知
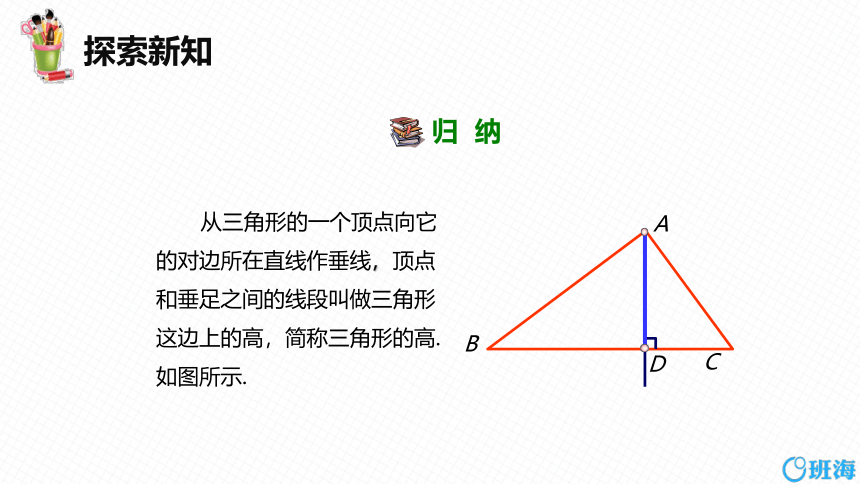
从三角形的一个顶点向它
的对边所在直线作垂线,顶点
和垂足之间的线段叫做三角形
这边上的高,简称三角形的高.
如图所示.
A
B
C
D
归 纳
探索新知
如图, 线段AD 是BC 边上的高.
A
B
C
注意:标明垂直的记号和垂足
的字母.
D
探索新知
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
O
锐角三角形的三条高是
在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
探索新知
直角三角形的三条高
在纸上画出一个直角三角形.
将你的结果与同伴进行交流.
A
B
C
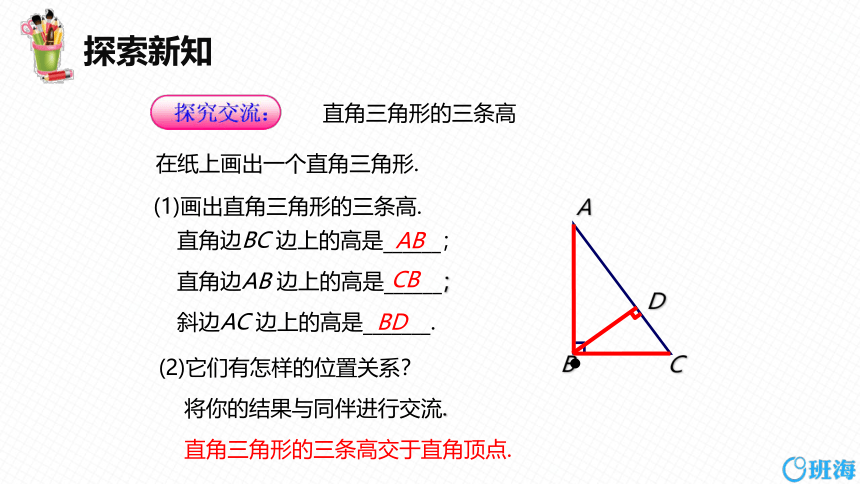
(1)画出直角三角形的三条高.
直角边BC 边上的高是______;
AB
直角边AB 边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC 边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
探索新知
A
B
C
D
E
F
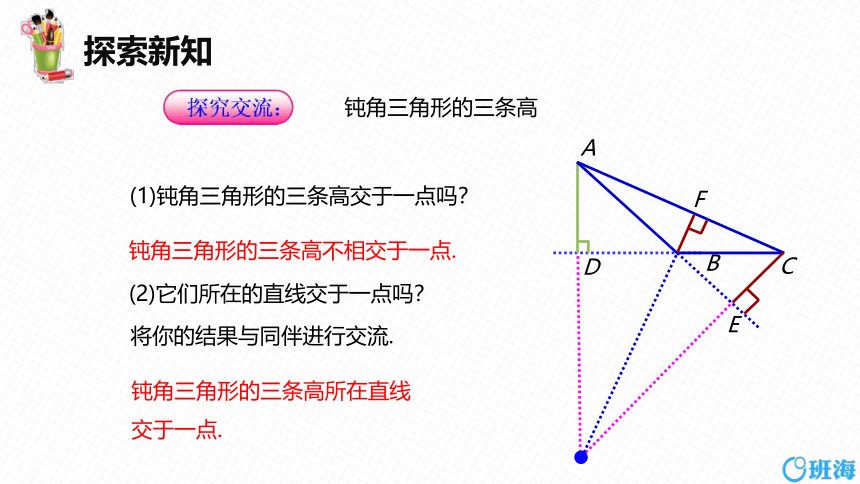
钝角三角形的三条高
(1)钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线
交于一点.
探索新知
_________________________叫做三角形这边上的高.
从三角形的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
归 纳
探索新知
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
探索新知
例1
画出下图中△ABC 的三条高.(要标明字母,不写画法)
“作一边上的高”,即可看成“过
一点(这边所对角的顶点)作已知直
线(这边所在的直线)的垂线.”按
照“过一点作已知直线的垂线”进
行作图,顶点与垂足之间的线段即为该边上的高;
需注意AB,BC 边上的高在三角形的外部,作高时
先延长AB 与CB.
导引:
探索新知
如图所示.
解:
探索新知
(1)作三角形的高时,找准顶点和对边是关键,作高的
步骤就是“过一点作已知直线的垂线”的步骤:
一靠(三角尺的一条直角边靠在要作高的边上)、
二找(移动三角尺使另一条直角边通过要作高的顶点)、
三画线(画垂线段),如图.
(2)注意:高是线段,垂线是直线.
总 结
典题精讲
1 如图,在△ABC 中,BC 边上的高是________;在△BCE 中,BE 边上的高是________;在△ACD 中,AC 边上的高是________.
AF
CE
CD
典题精讲
2 在△ABC 中,正确画出AC 边上的高的图形是( )
C
典题精讲
3 如图,△ABC 的面积为16,点D 是BC 边上一点,且BD= BC,点G 是AB上一点,点H 在△ABC 内部,且四边形BDHG 是平行四边形,则图中阴影部分的面积是( )
A.3
B.4
C.5
D.6
B
探索新知
知识点
知识点
三角形高的位置
做一做
每人准备一个锐角三角形纸片.
(1)你能画出这个三角形的三条高吗?你能用折纸的方
法得到它们吗
(2)这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
2
探索新知
知识点
议一议
在纸上画出一个直角三角形和一个钝角三角形.
(1)画出直角三角形的三条高,它们有怎样的位置关系?(2)你能折出钝角三角形的三条高吗?你能画出它们吗?
(3)钝角三角形的三条高交于一点吗?它们所在的直线
交于一点吗?将你的结果与同伴进行交流.
探索新知
知识点
三角形的三条高所在的直线交于一点.
归 纳
探索新知
知识点
位置图例:
(1)三个角都是锐角的三角形:三条高都在
三角形的内部,其交点也在三角形的内
部(如图①);
(2)有一个直角的三角形:一条高在三角形
的内部,其余两条高在三角形边上;其
交点为直角顶点(如图②);
(3)有一个钝角的三角形:一条高在三角形
的内部,其余两条高在三角形的外部,
其所在直线的交点在三角形的外部(如图③).
探索新知
知识点
例2
如图,在△ABC 中,BC 边上的高AD=4cm,
BC=4cm,AC=5cm.
(1)试求△ABC 的面积及AC 边上的高BE 的长;
(2)试求AD∶BE 的值.
利用三角形面积公式及面
积法求解.
导引:
探索新知
知识点
(1)S△ABC= BC · AD= ×4×4=8(cm2),
因为S△ABC= AC · BE= ×5×BE=8(cm2),
所以BE= cm.
(2)AD∶BE=4∶ =
解:
探索新知
知识点
求三角形的面积联想三角形的高,求三角形的
高联想三角形的面积是解三角形问题中常用的思想
方法之一,而用同一个三角形不同的面积表达式建
立求线段长度的等量关系,是一种很重要的数学方
法:面积法.
总 结
探索新知
知识点
例3
如图,已知△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.试说明:BG=DE+DF.
要说明线段的和、差关系,需将它
们转化为三角形的高的和、差关系,
再利用面积的和、差关系来解决.
其中只有BG 是△ABC 的高.
DE,DF 要想成为高,很自然地联想
到要连接AD.
导引:
探索新知
知识点
如图,连接AD,因为S△ABC=S△ABD+S△ADC,
所以 AC·BG= AB·DE+ AC·DF.
又因为AB=AC,
所以BG=DE+DF.
解:
探索新知
知识点
“面积法”是数学中很重要的方法,而在涉及垂
直的线段的关系时,常将线段的关系转化为面积的
关系来解决.
总 结
典题精讲
1
下图中,△ABC 的BC 边上的高画得对吗?若不对,请改正.
解:(1)对.(2)不对.改正如图.
(1)
(2)
典题精讲
2
如果一个三角形的三条高的交点恰是三角形的一个顶点,
那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.都有可能
C
典题精讲
3
不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
C
典题精讲
4
下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
学以致用
小试牛刀
下列结论:①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③三角形的中线可能在三角形外部;
④三角形的高都在三角形内部.
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
A
1
小试牛刀
2
已知AD 是△ABC 的高,∠BAD=72°,∠CAD=21°,求∠BAC 的度数.
当高AD 在△ABC 的内部时,如图①所示,∠BAC=∠BAD+∠CAD=93°;
当高AD 在△ABC 的外部时,如图②所示,∠BAC=∠BAD-∠CAD=51°.
解:
小试牛刀
3
如图,已知在△ABC 中,AB=AC=4,P 是BC 边上任一点,PD⊥AB,PE⊥AC,D,E 为垂足.若△ABC 的面积为6,问:PD+PE 的值能否确定?若能确定,值是多少?请说明理由.
小试牛刀
PD+PE 的值能确定,且PD+PE=3.
理由:如图,连接AP.
由图可得S△ABC=S△ABP+S△ACP.
因为PD⊥AB,PE⊥AC,AB=AC=4,△ABC 的面积为6,
所以6= ×4×PD+ ×4×PE=2(PD+PE ).
所以PD+PE=3.
解:
课堂小结
课堂小结
三角形的高线:
(1)定义;
(2)高线的画法;
(3)三角形的三条高线所在的直线相交于一点,这
一点叫做三角形的垂心.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
4.1认识三角形
第4课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
1.什么是三角形的中线?什么是三角形的角平分线?
2.三角形的三条中线、角平分线相交于一点吗?
这一交点在三角形的内部还是外部?
复
习
回
顾
新课精讲
探索新知
知识点
三角形的高
你能过三角形的一个顶点,你能画出它的对边的垂线吗
B
A
C
你还记得 “过一点画已知直线的垂线”吗
1
探索新知
从三角形的一个顶点向它
的对边所在直线作垂线,顶点
和垂足之间的线段叫做三角形
这边上的高,简称三角形的高.
如图所示.
A
B
C
D
归 纳
探索新知
如图, 线段AD 是BC 边上的高.
A
B
C
注意:标明垂直的记号和垂足
的字母.
D
探索新知
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
O
锐角三角形的三条高是
在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
探索新知
直角三角形的三条高
在纸上画出一个直角三角形.
将你的结果与同伴进行交流.
A
B
C
(1)画出直角三角形的三条高.
直角边BC 边上的高是______;
AB
直角边AB 边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC 边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
探索新知
A
B
C
D
E
F
钝角三角形的三条高
(1)钝角三角形的三条高交于一点吗?
(2)它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
钝角三角形的三条高不相交于一点.
钝角三角形的三条高所在直线
交于一点.
探索新知
_________________________叫做三角形这边上的高.
从三角形的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
归 纳
探索新知
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
探索新知
例1
画出下图中△ABC 的三条高.(要标明字母,不写画法)
“作一边上的高”,即可看成“过
一点(这边所对角的顶点)作已知直
线(这边所在的直线)的垂线.”按
照“过一点作已知直线的垂线”进
行作图,顶点与垂足之间的线段即为该边上的高;
需注意AB,BC 边上的高在三角形的外部,作高时
先延长AB 与CB.
导引:
探索新知
如图所示.
解:
探索新知
(1)作三角形的高时,找准顶点和对边是关键,作高的
步骤就是“过一点作已知直线的垂线”的步骤:
一靠(三角尺的一条直角边靠在要作高的边上)、
二找(移动三角尺使另一条直角边通过要作高的顶点)、
三画线(画垂线段),如图.
(2)注意:高是线段,垂线是直线.
总 结
典题精讲
1 如图,在△ABC 中,BC 边上的高是________;在△BCE 中,BE 边上的高是________;在△ACD 中,AC 边上的高是________.
AF
CE
CD
典题精讲
2 在△ABC 中,正确画出AC 边上的高的图形是( )
C
典题精讲
3 如图,△ABC 的面积为16,点D 是BC 边上一点,且BD= BC,点G 是AB上一点,点H 在△ABC 内部,且四边形BDHG 是平行四边形,则图中阴影部分的面积是( )
A.3
B.4
C.5
D.6
B
探索新知
知识点
知识点
三角形高的位置
做一做
每人准备一个锐角三角形纸片.
(1)你能画出这个三角形的三条高吗?你能用折纸的方
法得到它们吗
(2)这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
2
探索新知
知识点
议一议
在纸上画出一个直角三角形和一个钝角三角形.
(1)画出直角三角形的三条高,它们有怎样的位置关系?(2)你能折出钝角三角形的三条高吗?你能画出它们吗?
(3)钝角三角形的三条高交于一点吗?它们所在的直线
交于一点吗?将你的结果与同伴进行交流.
探索新知
知识点
三角形的三条高所在的直线交于一点.
归 纳
探索新知
知识点
位置图例:
(1)三个角都是锐角的三角形:三条高都在
三角形的内部,其交点也在三角形的内
部(如图①);
(2)有一个直角的三角形:一条高在三角形
的内部,其余两条高在三角形边上;其
交点为直角顶点(如图②);
(3)有一个钝角的三角形:一条高在三角形
的内部,其余两条高在三角形的外部,
其所在直线的交点在三角形的外部(如图③).
探索新知
知识点
例2
如图,在△ABC 中,BC 边上的高AD=4cm,
BC=4cm,AC=5cm.
(1)试求△ABC 的面积及AC 边上的高BE 的长;
(2)试求AD∶BE 的值.
利用三角形面积公式及面
积法求解.
导引:
探索新知
知识点
(1)S△ABC= BC · AD= ×4×4=8(cm2),
因为S△ABC= AC · BE= ×5×BE=8(cm2),
所以BE= cm.
(2)AD∶BE=4∶ =
解:
探索新知
知识点
求三角形的面积联想三角形的高,求三角形的
高联想三角形的面积是解三角形问题中常用的思想
方法之一,而用同一个三角形不同的面积表达式建
立求线段长度的等量关系,是一种很重要的数学方
法:面积法.
总 结
探索新知
知识点
例3
如图,已知△ABC 中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC.试说明:BG=DE+DF.
要说明线段的和、差关系,需将它
们转化为三角形的高的和、差关系,
再利用面积的和、差关系来解决.
其中只有BG 是△ABC 的高.
DE,DF 要想成为高,很自然地联想
到要连接AD.
导引:
探索新知
知识点
如图,连接AD,因为S△ABC=S△ABD+S△ADC,
所以 AC·BG= AB·DE+ AC·DF.
又因为AB=AC,
所以BG=DE+DF.
解:
探索新知
知识点
“面积法”是数学中很重要的方法,而在涉及垂
直的线段的关系时,常将线段的关系转化为面积的
关系来解决.
总 结
典题精讲
1
下图中,△ABC 的BC 边上的高画得对吗?若不对,请改正.
解:(1)对.(2)不对.改正如图.
(1)
(2)
典题精讲
2
如果一个三角形的三条高的交点恰是三角形的一个顶点,
那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.都有可能
C
典题精讲
3
不一定在三角形内部的线段是( )
A.三角形的角平分线
B.三角形的中线
C.三角形的高
D.以上都不对
C
典题精讲
4
下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
学以致用
小试牛刀
下列结论:①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③三角形的中线可能在三角形外部;
④三角形的高都在三角形内部.
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
A
1
小试牛刀
2
已知AD 是△ABC 的高,∠BAD=72°,∠CAD=21°,求∠BAC 的度数.
当高AD 在△ABC 的内部时,如图①所示,∠BAC=∠BAD+∠CAD=93°;
当高AD 在△ABC 的外部时,如图②所示,∠BAC=∠BAD-∠CAD=51°.
解:
小试牛刀
3
如图,已知在△ABC 中,AB=AC=4,P 是BC 边上任一点,PD⊥AB,PE⊥AC,D,E 为垂足.若△ABC 的面积为6,问:PD+PE 的值能否确定?若能确定,值是多少?请说明理由.
小试牛刀
PD+PE 的值能确定,且PD+PE=3.
理由:如图,连接AP.
由图可得S△ABC=S△ABP+S△ACP.
因为PD⊥AB,PE⊥AC,AB=AC=4,△ABC 的面积为6,
所以6= ×4×PD+ ×4×PE=2(PD+PE ).
所以PD+PE=3.
解:
课堂小结
课堂小结
三角形的高线:
(1)定义;
(2)高线的画法;
(3)三角形的三条高线所在的直线相交于一点,这
一点叫做三角形的垂心.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
