【班海精品】北师大版(新)七下-5.3简单的轴对称图形 第三课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-5.3简单的轴对称图形 第三课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:22:28 | ||
图片预览







文档简介
(共40张PPT)
5.3简单的轴对称图形
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图5-16,将∠AOB 对折,你发现了什么
角是生活中常见的图形,角是轴对称图形吗
情景导入
角是轴对称图形,角平分线所在的直线是它的对称轴.
总 结
新课精讲
探索新知
1
知识点
角平分线的画法
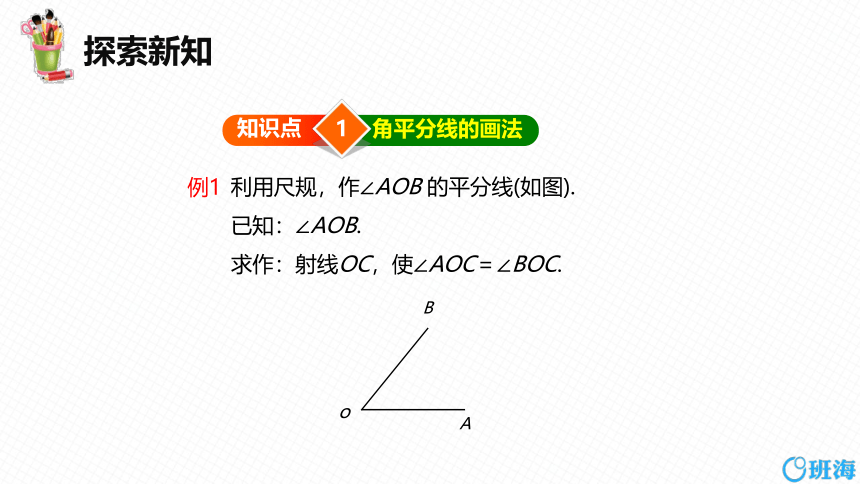
例1
利用尺规,作∠AOB 的平分线(如图).
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
A
B
o
探索新知
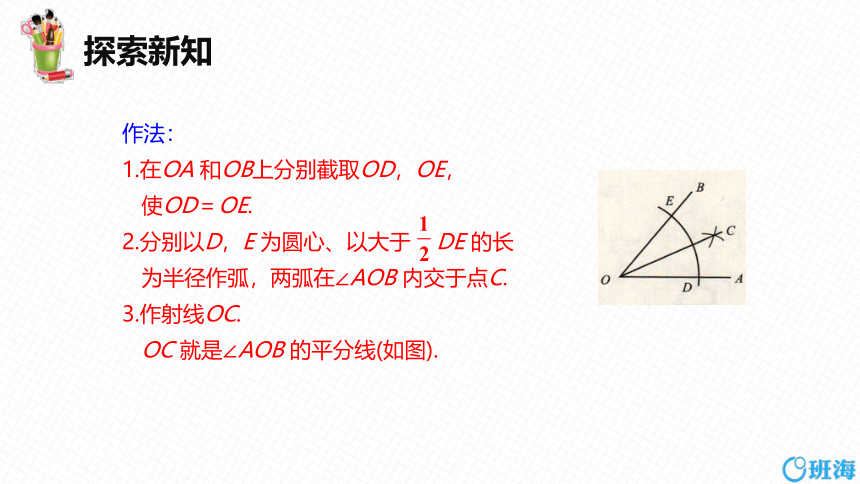
作法:
1.在OA 和OB上分别截取OD,OE,
使OD=OE.
2.分别以D,E 为圆心、以大于 DE 的长
为半径作弧,两弧在∠AOB 内交于点C.
3.作射线OC.
OC 就是∠AOB 的平分线(如图).
探索新知
例2
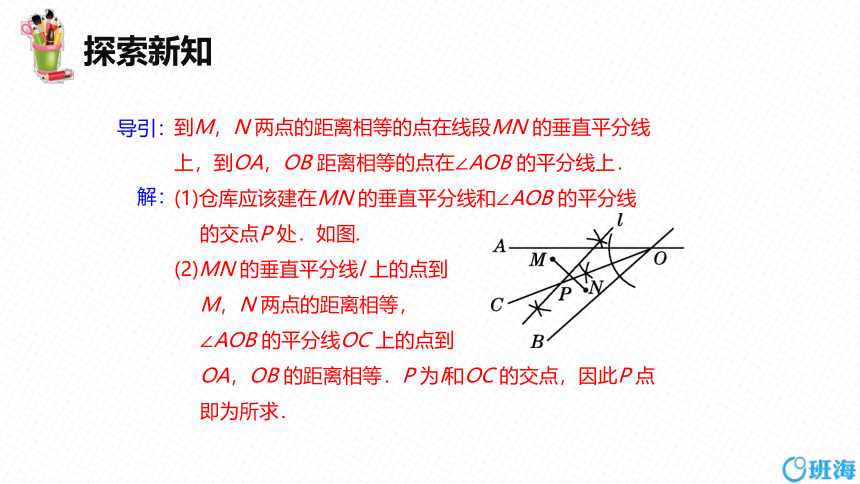
某地有两所大学和两条相交叉的公路,如图(点M,N 表示大学,AO,BO 表示公路).现计划在∠AOB 内修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形
中画出你的设计方案;
(2)阐述你的设计理由.
探索新知
到M,N 两点的距离相等的点在线段MN 的垂直平分线
上,到OA,OB 距离相等的点在∠AOB 的平分线上.
(1)仓库应该建在MN 的垂直平分线和∠AOB 的平分线
的交点P 处.如图.
(2)MN 的垂直平分线l 上的点到
M,N 两点的距离相等,
∠AOB 的平分线OC 上的点到
OA,OB 的距离相等.P 为l和OC 的交点,因此P 点
即为所求.
解:
导引:
典题精讲
1
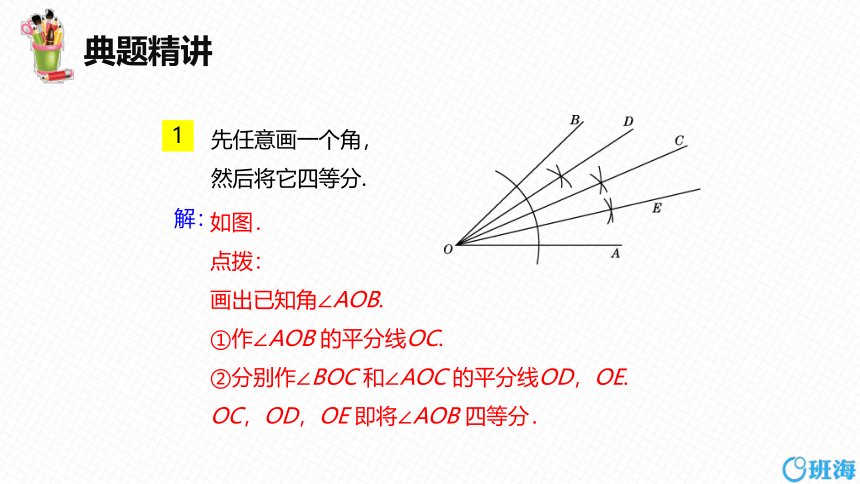
先任意画一个角,
然后将它四等分.
如图.
点拨:
画出已知角∠AOB.
①作∠AOB 的平分线OC.
②分别作∠BOC 和∠AOC 的平分线OD,OE. OC,OD,OE 即将∠AOB 四等分.
解:
典题精讲
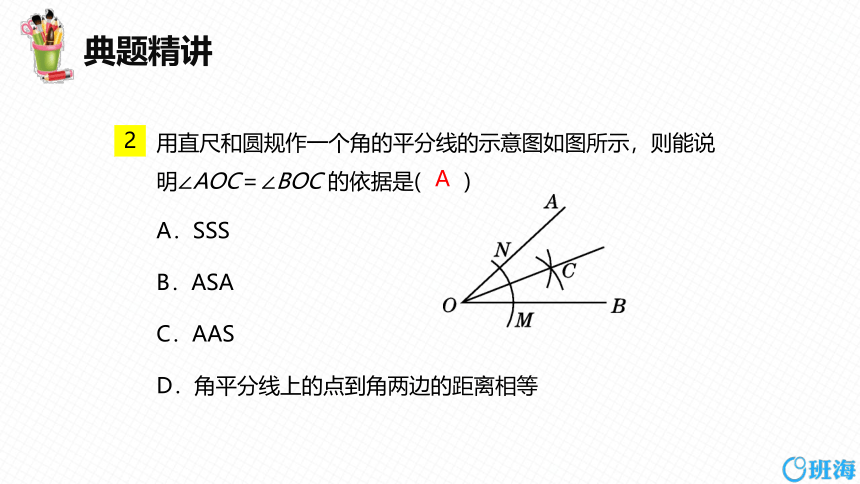
2
用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC 的依据是( )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
典题精讲
3
作∠AOB 的平分线时,以O 为圆心,某一长度为半径作弧,与OA,OB 分别相交于C,D,然后分别以C,D 为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A.大于 CD B.等于 CD
C.小于 CD D.以上都不对
A
探索新知
知识点
角平分线的性质
做一做
(1)在一张纸上任意画∠AOB,沿角的
两边将角剪下,将这个角对折,使
角的两边重合,折痕就是∠AOB 的
平分线.
(2)在∠AOB 的角平分线上任意取一点C,分别折出过点C
且与∠AOB 的两边垂直的直线,垂足分别为D,E,将
∠AOB 再次对折, 线段CD 与CE 能重合吗?
改变点C 的位置,线段CD 和CE 还相等吗
2
探索新知
1.角是轴对称图形,角平分线所在的直线是它的对称轴.
2.角平分线的性质:角平分线上的点到这个角的两边的距离相等.
探索新知
例3
如图,在△ABC 中,∠C=90°,AD 平分∠BAC,若BC=5 cm,BD=3 cm,则点D 到AB 的距离为_____.
点D 到AB 的距离就是过点D 作AB 的
垂线段的长度.过D 作DE⊥AB 于E.
因为∠C=90°,AD 平分∠BAC,
所以ED=CD=BC-BD=5-3=
2(cm).
导引:
2cm
探索新知
求角平分线上的点到角两边的距离时,应用角平
分线的性质将未知线段向已知线段转化.
总 结
探索新知
例4
如图,BD 是∠ABC 的平分线,BA=BC,点P 在BD上,PM⊥AD,PN⊥CD,垂足分别为M,N,试说明:PM=PN.
要说明PM=PN,由PM⊥AD,
PN⊥CD,可说明PMD ≌△PND
或者DP 平分∠ADC. 题目已知BD
平分∠ABC,所以用第二种方法
更简单些.
导引:
探索新知
因为BD 平分∠ABC,所以∠ABD=∠CBD.
因为BA=BC,BD=BD,
所以△ABD ≌△CBD (SAS),
所以∠ADB=∠CDB.
又因为PM⊥AD,PN⊥CD,所以PM=PN.
解:
探索新知
用角平分线的性质说明两条线段相等,就不用再说明两条线段所在的三角形全等.性质的具体运用是:一平分两垂直得相等.
总 结
典题精讲
1
如图,OP 为∠AOB 的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
B
典题精讲
2
如图,OP 平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO 平分∠APB
C.OA=OB
D.AB 垂直平分OP
D
典题精讲
3
如图,点P 是∠AOB 平分线OC 上一点,PD⊥OB,垂足为D,若PD=2,则点P 到边OA 的距离是( )
A.2
B.3
C.
D.4
A
典题精讲
4
如图,在△ABC 中,∠C=90°,AC=BC,AD 平分∠CAB交BC 于D,DE⊥AB 于E,若AB=6 cm,则△DBE 的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
易错提醒
如图,在△ABC 中,BD 平分∠ABC,交AC 于点D,BC 边上有一点E,连接DE,则AD 与DE 的关系为( )
A.AD >DE B.AD=DE
C.AD易错点:运用角的平分线的性质时,常因忽略“到角两边的距离”而导致错误
D
学以致用
小试牛刀
如图,在Rt△ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点M,N,再分别以点M,N 为圆心,大于 MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=4,AB=15,则△ABD 的面积是( )
A.15 B.30
C.45 D.60
D
1
小试牛刀
如图,AB∥CD,BP 和CP 分别平分∠ABC 和∠DCB,AD 过点P,且与AB 垂直.若AD=8,则点P 到BC 的距离是( )
A.8
B.6
C.4
D.2
C
2
小试牛刀
3
证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P 在OC上,_________________________________________.
求证:________.
请你补全已知和求证,并写出证明过程.
PD⊥OA,PE⊥OB,垂足分别为D,E
PD=PE
小试牛刀
因为PD⊥OA,PE⊥OB,
所以∠PDO=∠PEO=90°.
在△PDO 和△PEO 中,
所以△PDO ≌△PEO (AAS).所以PD=PE.
证明:
小试牛刀
4
如图,在四边形ABCD 中,∠B=90°,AB∥CD,M 为BC 边上的一点,且AM 平分∠BAD,DM 平分∠ADC.
试说明:
(1)AM⊥DM;
(2)M 为BC 的中点.
小试牛刀
(1)因为AB∥CD,
所以∠BAD+∠ADC=180°.
因为AM 平分∠BAD,DM 平分∠ADC,
所以∠BAD=2∠MAD,∠ADC=2∠ADM.
所以2∠MAD+2∠ADM=180°.
所以∠MAD+∠ADM=90°.
所以∠AMD=90°,即AM⊥DM.
解:
小试牛刀
(2)如图,作MN⊥AD 交AD 于N,
因为∠B=90°,AB∥CD,
所以BM⊥AB,CM⊥CD,
因为AM 平分∠BAD,DM 平分∠ADC,
所以MB=MN,MN=MC,
所以MB=MC,
即M 为BC 的中点.
小试牛刀
5
如图,在四边形ABCD 中,AC 为∠BAD 的平分线,AB=AD,点E,F 分别在AB,AD上,且AE=DF,请完整说明为何四边形AECF 的面积为四边形ABCD 面积的一半.
小试牛刀
如图,作CG⊥AB 于G,CH⊥AD 于H.
因为AC 为∠BAD 的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ADC= S四边形ABCD
又因为AE=DF,所以S△AEC=S△DFC
所以S四边形AECF=S△AEC+S△ACF=S△DFC+S△ACF=
S△ACD= S四边形ABCD,
即四边形AECF 的面积为四边形ABCD 面积的一半.
解:
小试牛刀
6
感知:如图①,AD 平分∠BAC,∠B+∠C=180°,∠B=90°.
易知:DB=DC.
探究:如图②,AD 平分∠BAC,∠ABD+∠ACD=180°,
∠ABD<90°.试说明:DB=DC.
小试牛刀
如图,过点D 分别作DE⊥AB 于E,DF⊥AC 交AC的延长线于F.
因为AD 平分∠BAC,DE⊥AB,DF⊥AC,
所以DE=DF.
因为∠B+∠ACD=180°,
∠ACD+∠FCD=180°,
所以∠B=∠FCD.
在△DFC 和△DEB 中,
所以△DFC ≌△DEB (AAS).所以DC=DB.
解:
课堂小结
角的平分线图形结构中的“两种数量关系”:
如图,OC 平分∠AOB,PD⊥OA于D,
PE⊥OB 于E,DE 交OC 于点F.
(1)角的相等关系:
①∠AOC=∠BOC=∠PDF=∠PEF;
②∠ODP=∠OEP=∠DFO=∠EFO=∠DFP=
∠EFP=90°;
③∠DPO=∠EPO=∠ODF=∠OEF.
(2)线段的相等关系:OD=OE,DP=EP,DF=EF.
课堂小结
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.3简单的轴对称图形
第3课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
如图5-16,将∠AOB 对折,你发现了什么
角是生活中常见的图形,角是轴对称图形吗
情景导入
角是轴对称图形,角平分线所在的直线是它的对称轴.
总 结
新课精讲
探索新知
1
知识点
角平分线的画法
例1
利用尺规,作∠AOB 的平分线(如图).
已知:∠AOB.
求作:射线OC,使∠AOC=∠BOC.
A
B
o
探索新知
作法:
1.在OA 和OB上分别截取OD,OE,
使OD=OE.
2.分别以D,E 为圆心、以大于 DE 的长
为半径作弧,两弧在∠AOB 内交于点C.
3.作射线OC.
OC 就是∠AOB 的平分线(如图).
探索新知
例2
某地有两所大学和两条相交叉的公路,如图(点M,N 表示大学,AO,BO 表示公路).现计划在∠AOB 内修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.
(1)你能确定仓库应该建在什么位置吗?在所给的图形
中画出你的设计方案;
(2)阐述你的设计理由.
探索新知
到M,N 两点的距离相等的点在线段MN 的垂直平分线
上,到OA,OB 距离相等的点在∠AOB 的平分线上.
(1)仓库应该建在MN 的垂直平分线和∠AOB 的平分线
的交点P 处.如图.
(2)MN 的垂直平分线l 上的点到
M,N 两点的距离相等,
∠AOB 的平分线OC 上的点到
OA,OB 的距离相等.P 为l和OC 的交点,因此P 点
即为所求.
解:
导引:
典题精讲
1
先任意画一个角,
然后将它四等分.
如图.
点拨:
画出已知角∠AOB.
①作∠AOB 的平分线OC.
②分别作∠BOC 和∠AOC 的平分线OD,OE. OC,OD,OE 即将∠AOB 四等分.
解:
典题精讲
2
用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC 的依据是( )
A.SSS
B.ASA
C.AAS
D.角平分线上的点到角两边的距离相等
A
典题精讲
3
作∠AOB 的平分线时,以O 为圆心,某一长度为半径作弧,与OA,OB 分别相交于C,D,然后分别以C,D 为圆心,适当的长度为半径作弧,使两弧相交于一点,则这个适当的长度为( )
A.大于 CD B.等于 CD
C.小于 CD D.以上都不对
A
探索新知
知识点
角平分线的性质
做一做
(1)在一张纸上任意画∠AOB,沿角的
两边将角剪下,将这个角对折,使
角的两边重合,折痕就是∠AOB 的
平分线.
(2)在∠AOB 的角平分线上任意取一点C,分别折出过点C
且与∠AOB 的两边垂直的直线,垂足分别为D,E,将
∠AOB 再次对折, 线段CD 与CE 能重合吗?
改变点C 的位置,线段CD 和CE 还相等吗
2
探索新知
1.角是轴对称图形,角平分线所在的直线是它的对称轴.
2.角平分线的性质:角平分线上的点到这个角的两边的距离相等.
探索新知
例3
如图,在△ABC 中,∠C=90°,AD 平分∠BAC,若BC=5 cm,BD=3 cm,则点D 到AB 的距离为_____.
点D 到AB 的距离就是过点D 作AB 的
垂线段的长度.过D 作DE⊥AB 于E.
因为∠C=90°,AD 平分∠BAC,
所以ED=CD=BC-BD=5-3=
2(cm).
导引:
2cm
探索新知
求角平分线上的点到角两边的距离时,应用角平
分线的性质将未知线段向已知线段转化.
总 结
探索新知
例4
如图,BD 是∠ABC 的平分线,BA=BC,点P 在BD上,PM⊥AD,PN⊥CD,垂足分别为M,N,试说明:PM=PN.
要说明PM=PN,由PM⊥AD,
PN⊥CD,可说明PMD ≌△PND
或者DP 平分∠ADC. 题目已知BD
平分∠ABC,所以用第二种方法
更简单些.
导引:
探索新知
因为BD 平分∠ABC,所以∠ABD=∠CBD.
因为BA=BC,BD=BD,
所以△ABD ≌△CBD (SAS),
所以∠ADB=∠CDB.
又因为PM⊥AD,PN⊥CD,所以PM=PN.
解:
探索新知
用角平分线的性质说明两条线段相等,就不用再说明两条线段所在的三角形全等.性质的具体运用是:一平分两垂直得相等.
总 结
典题精讲
1
如图,OP 为∠AOB 的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是( )
A.PC=PD
B.∠CPO=∠DOP
C.∠CPO=∠DPO
D.OC=OD
B
典题精讲
2
如图,OP 平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
A.PA=PB
B.PO 平分∠APB
C.OA=OB
D.AB 垂直平分OP
D
典题精讲
3
如图,点P 是∠AOB 平分线OC 上一点,PD⊥OB,垂足为D,若PD=2,则点P 到边OA 的距离是( )
A.2
B.3
C.
D.4
A
典题精讲
4
如图,在△ABC 中,∠C=90°,AC=BC,AD 平分∠CAB交BC 于D,DE⊥AB 于E,若AB=6 cm,则△DBE 的周长是( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
A
易错提醒
如图,在△ABC 中,BD 平分∠ABC,交AC 于点D,BC 边上有一点E,连接DE,则AD 与DE 的关系为( )
A.AD >DE B.AD=DE
C.AD
D
学以致用
小试牛刀
如图,在Rt△ABC 中,∠C=90°,以顶点A 为圆心,适当长为半径画弧,分别交AC,AB 于点M,N,再分别以点M,N 为圆心,大于 MN 的长为半径画弧,两弧交于点P,作射线AP 交边BC 于点D,若CD=4,AB=15,则△ABD 的面积是( )
A.15 B.30
C.45 D.60
D
1
小试牛刀
如图,AB∥CD,BP 和CP 分别平分∠ABC 和∠DCB,AD 过点P,且与AB 垂直.若AD=8,则点P 到BC 的距离是( )
A.8
B.6
C.4
D.2
C
2
小试牛刀
3
证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P 在OC上,_________________________________________.
求证:________.
请你补全已知和求证,并写出证明过程.
PD⊥OA,PE⊥OB,垂足分别为D,E
PD=PE
小试牛刀
因为PD⊥OA,PE⊥OB,
所以∠PDO=∠PEO=90°.
在△PDO 和△PEO 中,
所以△PDO ≌△PEO (AAS).所以PD=PE.
证明:
小试牛刀
4
如图,在四边形ABCD 中,∠B=90°,AB∥CD,M 为BC 边上的一点,且AM 平分∠BAD,DM 平分∠ADC.
试说明:
(1)AM⊥DM;
(2)M 为BC 的中点.
小试牛刀
(1)因为AB∥CD,
所以∠BAD+∠ADC=180°.
因为AM 平分∠BAD,DM 平分∠ADC,
所以∠BAD=2∠MAD,∠ADC=2∠ADM.
所以2∠MAD+2∠ADM=180°.
所以∠MAD+∠ADM=90°.
所以∠AMD=90°,即AM⊥DM.
解:
小试牛刀
(2)如图,作MN⊥AD 交AD 于N,
因为∠B=90°,AB∥CD,
所以BM⊥AB,CM⊥CD,
因为AM 平分∠BAD,DM 平分∠ADC,
所以MB=MN,MN=MC,
所以MB=MC,
即M 为BC 的中点.
小试牛刀
5
如图,在四边形ABCD 中,AC 为∠BAD 的平分线,AB=AD,点E,F 分别在AB,AD上,且AE=DF,请完整说明为何四边形AECF 的面积为四边形ABCD 面积的一半.
小试牛刀
如图,作CG⊥AB 于G,CH⊥AD 于H.
因为AC 为∠BAD 的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ADC= S四边形ABCD
又因为AE=DF,所以S△AEC=S△DFC
所以S四边形AECF=S△AEC+S△ACF=S△DFC+S△ACF=
S△ACD= S四边形ABCD,
即四边形AECF 的面积为四边形ABCD 面积的一半.
解:
小试牛刀
6
感知:如图①,AD 平分∠BAC,∠B+∠C=180°,∠B=90°.
易知:DB=DC.
探究:如图②,AD 平分∠BAC,∠ABD+∠ACD=180°,
∠ABD<90°.试说明:DB=DC.
小试牛刀
如图,过点D 分别作DE⊥AB 于E,DF⊥AC 交AC的延长线于F.
因为AD 平分∠BAC,DE⊥AB,DF⊥AC,
所以DE=DF.
因为∠B+∠ACD=180°,
∠ACD+∠FCD=180°,
所以∠B=∠FCD.
在△DFC 和△DEB 中,
所以△DFC ≌△DEB (AAS).所以DC=DB.
解:
课堂小结
角的平分线图形结构中的“两种数量关系”:
如图,OC 平分∠AOB,PD⊥OA于D,
PE⊥OB 于E,DE 交OC 于点F.
(1)角的相等关系:
①∠AOC=∠BOC=∠PDF=∠PEF;
②∠ODP=∠OEP=∠DFO=∠EFO=∠DFP=
∠EFP=90°;
③∠DPO=∠EPO=∠ODF=∠OEF.
(2)线段的相等关系:OD=OE,DP=EP,DF=EF.
课堂小结
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
