【班海精品】北师大版(新)七下-5.4利用轴对称进行设计【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-5.4利用轴对称进行设计【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览











文档简介
(共32张PPT)
5.4利用轴对称
进行设计
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
剪纸在生活中经常见到,你知道它是利用图形的
轴对称性进行设计的吗?
新课精讲
探索新知
1
知识点
剪纸中的轴对称
做一做
1.取一张长30 cm、宽6 cm的纸条,将它每3 cm一段,
一反一正像“手风琴”那样折叠起来.在折叠好的纸上画
出字母E,并用小刀把画出的字母E挖去. 拉开“手风琴”
纸条,你就可以得到一条以字母E为图案的花边.
探索新知
在上面的活动中,如果先把纸条纵向对折,再折成“手风琴”,然后继续上面的步骤,此时会得到怎样的花边?它是轴对称图形吗?先猜一猜,再做 一做.
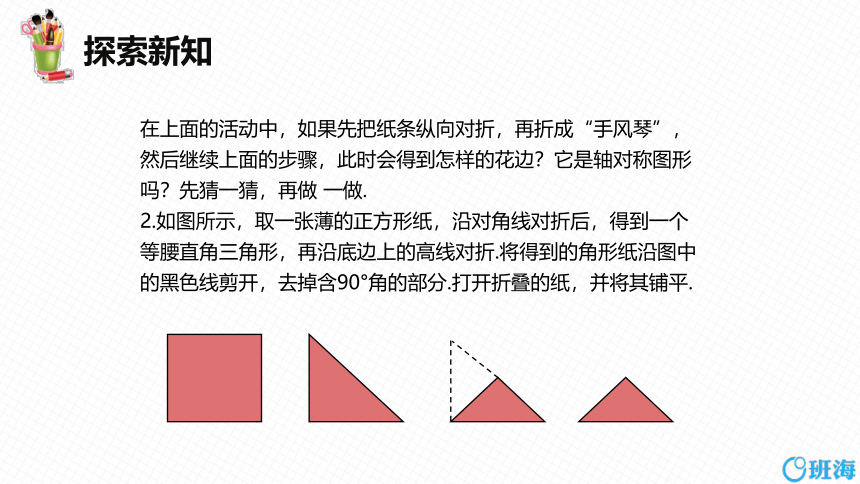
2.如图所示,取一张薄的正方形纸,沿对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折.将得到的角形纸沿图中的黑色线剪开,去掉含90°角的部分.打开折叠的纸,并将其铺平.
探索新知
(1)你会得到怎样的图案?先猜一猜,再做一做.
(2)你能说明为什么会得到这样的图案吗?应用学过的
轴对称知识试一试.
(3)如果将正方形纸按上面方式对折3
次(如图所示),然后沿圆弧剪开,
去掉较小部分,展开后结果又会
怎样?为什么?
(4)当纸对折2次后,剪出的图案至少有几条对称轴?
3次呢?
1. 已知轴对称图形,求作它的对称轴,先确定图形的
两个对应点,再作以这两个对应点为端点的线段的
垂直平分线,这条直线就是它的对称轴.
2.已知一点A 和对称轴l,求作点A 关于l 的对称点,可
按如下步骤进行:
(1)过点A 作直线l 的垂线段,垂足为B;
(2)延长AB 到A′,使BA′=AB.
点A′就是点A 关于l 的对称点.
如图.
探索新知
探索新知
3.剪纸的原理是轴对称和轴对称图形的性质的应用,
纸上的折痕所在的直线就是相邻两个图案的对称
轴.剪纸的步骤是:折—画—剪—展.
探索新知
剪纸是中国的民间艺术,剪纸方法很多,如图所示是一种剪纸方法的图示(先将纸折叠两次后剪去右下角,然后再展开即得到图案).
下列的四个图案中,不能用上述方法剪出的是( )
C
根据题意知按该方法折叠剪出的图案应是轴对称图形,而
四个选项中只有C不是轴对称图形,故不能剪出C.
导引:
例1
探索新知
本题应用排除法,C不是轴对称图形.
总 结
探索新知
例2
仔细观察下图的折纸、剪纸过程,并探索其规律.
探索新知
(1)要得到一个六角星,那么在第二步的折纸过程中需折
几次?得到的六角星有几条对称轴?剪一剪,试一试;
(2)要得到有8条对称轴的多角星,那么在第二步的折纸过
程中需折几次?得到几角星?
(1)要得到一个六角星,那么在第二步的折纸过程中需
折5次,得到的六角星有6条对称轴.
(2)要得到有8条对称轴的多角星,那么在第二步的折纸
过程中需折7次,得到八角星.
解:
探索新知
本题在对剪纸理解的基础上可用归纳法总结出规律,然后再进行验证.
总 结
典题精讲
1
用一张正方形的红纸沿对角线对折后,得到一个等腰直角三角形,再沿斜边上的高对折,得到的又是等腰直角三角形,在此三角形上剪出一些花纹,然后打开折叠的纸,将它铺平,小明一下子就猜出了这个图案至少有( )条对称轴.
A.0 B.2
C.4 D.6
B
典题精讲
2 剪纸是中国的民间艺术,剪纸的方法有很多,下面是一种剪纸的方法.如图,先将纸折叠,然后剪出图形,再展开,即可得到图案.
下面四个图案中,不能用上述方法剪出的是( )
C
探索新知
2
知识点
设计轴对称图案
做一做
生活中有很多具有轴对称性质的图案,例如:
你知道这些图案的含义吗?自己设计一个轴对称
图案,并说明你的设计意图.
探索新知
例3
取一张长18 cm,宽5 cm的纸条,将它每3 cm一段,一反一正像“手风琴”那样折叠起来,并在折叠好的纸上画出字母S,用小刀把画出的字母S挖去,拉“手风琴”,你就可以得到一条以字母S为图案的花边,如图.
(1)在你所得的花边中,相邻两个图案有什么关系?说说你的理由.
(2)如果以相邻两个图案为一组,每组图案之间有什么关系?三个图案为一组呢?为什么?
探索新知
(1)相邻两个图案成轴对称,因为相邻两个S间有一条折痕,这条折痕所在直线就是对称轴;
(2)以相邻两个图案为一组,每组图案之间成轴对称;三个图案为一组,每组图案之间成轴对称,因为在这两组图案之间都能找到折叠过程中的折叠痕迹.
解:
探索新知
经过折叠、剪切后得到的图案都是轴对称图形,
折痕所在直线是相邻两个图形的对称轴.
总 结
探索新知
例4
以给出的图形“○○,△△,===”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
探索新知
能;答案不唯一,如图.
解:
典题精讲
1 如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
A.4个 B.3个
C.2个 D.1个
A
典题精讲
2 如图,在3×3的正方形网格中已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的办法有( )种.
A.3
B.4
C.5
D.6
C
学以致用
小试牛刀
如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
A.①② B.①③ C.①④ D.③⑤
B
1
小试牛刀
2
将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
小试牛刀
能;答案不唯一,如图.
解:
课堂小结
课堂小结
1.在设计图案时需要注意“三点”:
(1)图案是由哪些基本图形组成的;
(2)是不是轴对称图形.如果是轴对称图形,要先确定它的对称轴;
(3)设计轴对称性质的图案时,除图形对称外,有时颜色也要“对称”.
2.把一张卡纸经过一次或多次折叠完全重合后,卡纸展开得到的图案显然是轴对称图案.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
5.4利用轴对称
进行设计
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
剪纸在生活中经常见到,你知道它是利用图形的
轴对称性进行设计的吗?
新课精讲
探索新知
1
知识点
剪纸中的轴对称
做一做
1.取一张长30 cm、宽6 cm的纸条,将它每3 cm一段,
一反一正像“手风琴”那样折叠起来.在折叠好的纸上画
出字母E,并用小刀把画出的字母E挖去. 拉开“手风琴”
纸条,你就可以得到一条以字母E为图案的花边.
探索新知
在上面的活动中,如果先把纸条纵向对折,再折成“手风琴”,然后继续上面的步骤,此时会得到怎样的花边?它是轴对称图形吗?先猜一猜,再做 一做.
2.如图所示,取一张薄的正方形纸,沿对角线对折后,得到一个等腰直角三角形,再沿底边上的高线对折.将得到的角形纸沿图中的黑色线剪开,去掉含90°角的部分.打开折叠的纸,并将其铺平.
探索新知
(1)你会得到怎样的图案?先猜一猜,再做一做.
(2)你能说明为什么会得到这样的图案吗?应用学过的
轴对称知识试一试.
(3)如果将正方形纸按上面方式对折3
次(如图所示),然后沿圆弧剪开,
去掉较小部分,展开后结果又会
怎样?为什么?
(4)当纸对折2次后,剪出的图案至少有几条对称轴?
3次呢?
1. 已知轴对称图形,求作它的对称轴,先确定图形的
两个对应点,再作以这两个对应点为端点的线段的
垂直平分线,这条直线就是它的对称轴.
2.已知一点A 和对称轴l,求作点A 关于l 的对称点,可
按如下步骤进行:
(1)过点A 作直线l 的垂线段,垂足为B;
(2)延长AB 到A′,使BA′=AB.
点A′就是点A 关于l 的对称点.
如图.
探索新知
探索新知
3.剪纸的原理是轴对称和轴对称图形的性质的应用,
纸上的折痕所在的直线就是相邻两个图案的对称
轴.剪纸的步骤是:折—画—剪—展.
探索新知
剪纸是中国的民间艺术,剪纸方法很多,如图所示是一种剪纸方法的图示(先将纸折叠两次后剪去右下角,然后再展开即得到图案).
下列的四个图案中,不能用上述方法剪出的是( )
C
根据题意知按该方法折叠剪出的图案应是轴对称图形,而
四个选项中只有C不是轴对称图形,故不能剪出C.
导引:
例1
探索新知
本题应用排除法,C不是轴对称图形.
总 结
探索新知
例2
仔细观察下图的折纸、剪纸过程,并探索其规律.
探索新知
(1)要得到一个六角星,那么在第二步的折纸过程中需折
几次?得到的六角星有几条对称轴?剪一剪,试一试;
(2)要得到有8条对称轴的多角星,那么在第二步的折纸过
程中需折几次?得到几角星?
(1)要得到一个六角星,那么在第二步的折纸过程中需
折5次,得到的六角星有6条对称轴.
(2)要得到有8条对称轴的多角星,那么在第二步的折纸
过程中需折7次,得到八角星.
解:
探索新知
本题在对剪纸理解的基础上可用归纳法总结出规律,然后再进行验证.
总 结
典题精讲
1
用一张正方形的红纸沿对角线对折后,得到一个等腰直角三角形,再沿斜边上的高对折,得到的又是等腰直角三角形,在此三角形上剪出一些花纹,然后打开折叠的纸,将它铺平,小明一下子就猜出了这个图案至少有( )条对称轴.
A.0 B.2
C.4 D.6
B
典题精讲
2 剪纸是中国的民间艺术,剪纸的方法有很多,下面是一种剪纸的方法.如图,先将纸折叠,然后剪出图形,再展开,即可得到图案.
下面四个图案中,不能用上述方法剪出的是( )
C
探索新知
2
知识点
设计轴对称图案
做一做
生活中有很多具有轴对称性质的图案,例如:
你知道这些图案的含义吗?自己设计一个轴对称
图案,并说明你的设计意图.
探索新知
例3
取一张长18 cm,宽5 cm的纸条,将它每3 cm一段,一反一正像“手风琴”那样折叠起来,并在折叠好的纸上画出字母S,用小刀把画出的字母S挖去,拉“手风琴”,你就可以得到一条以字母S为图案的花边,如图.
(1)在你所得的花边中,相邻两个图案有什么关系?说说你的理由.
(2)如果以相邻两个图案为一组,每组图案之间有什么关系?三个图案为一组呢?为什么?
探索新知
(1)相邻两个图案成轴对称,因为相邻两个S间有一条折痕,这条折痕所在直线就是对称轴;
(2)以相邻两个图案为一组,每组图案之间成轴对称;三个图案为一组,每组图案之间成轴对称,因为在这两组图案之间都能找到折叠过程中的折叠痕迹.
解:
探索新知
经过折叠、剪切后得到的图案都是轴对称图形,
折痕所在直线是相邻两个图形的对称轴.
总 结
探索新知
例4
以给出的图形“○○,△△,===”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗?请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
探索新知
能;答案不唯一,如图.
解:
典题精讲
1 如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有( )
A.4个 B.3个
C.2个 D.1个
A
典题精讲
2 如图,在3×3的正方形网格中已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的办法有( )种.
A.3
B.4
C.5
D.6
C
学以致用
小试牛刀
如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是( )
A.①② B.①③ C.①④ D.③⑤
B
1
小试牛刀
2
将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
小试牛刀
能;答案不唯一,如图.
解:
课堂小结
课堂小结
1.在设计图案时需要注意“三点”:
(1)图案是由哪些基本图形组成的;
(2)是不是轴对称图形.如果是轴对称图形,要先确定它的对称轴;
(3)设计轴对称性质的图案时,除图形对称外,有时颜色也要“对称”.
2.把一张卡纸经过一次或多次折叠完全重合后,卡纸展开得到的图案显然是轴对称图案.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
