【班海精品】北师大版(新)七下-6.2频率的稳定性 第一课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-6.2频率的稳定性 第一课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览










文档简介
(共44张PPT)
6.2频率的稳定性
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
掷一枚图钉,落地后会出现两种情况:
你认为钉尖朝上和钉尖朝下的可能性一样大吗
新课精讲
探索新知
1
知识点
频 率
探索新知
(1)两人一组做20次掷图钉的游戏,并将数据记录在下表中:
试验总次数
钉尖朝上的次数
钉尖朝下的次数
钉尖朝上的频率
钉尖朝下的频率
探索新知
定义:在n 次重复试验中,不确定事件A 发生了m 次,则比值 称为事件A 发生的频率.
探索新知
例1
在一个不透明的盒子中装有n 个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n 大约是________.
10
探索新知
例2
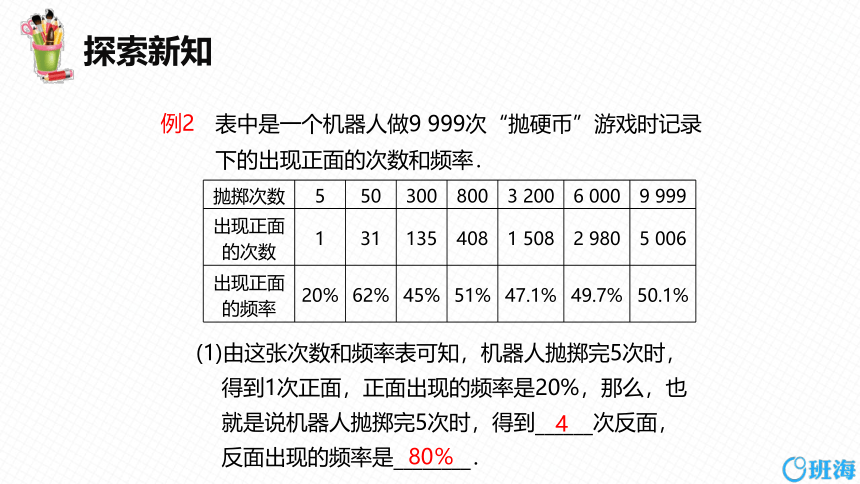
表中是一个机器人做9 999次“抛硬币”游戏时记录下的出现正面的次数和频率.
抛掷次数 5 50 300 800 3 200 6 000 9 999
出现正面 的次数 1 31 135 408 1 508 2 980 5 006
出现正面 的频率 20% 62% 45% 51% 47.1% 49.7% 50.1%
(1)由这张次数和频率表可知,机器人抛掷完5次时,
得到1次正面,正面出现的频率是20%,那么,也
就是说机器人抛掷完5次时,得到______次反面,
反面出现的频率是________.
4
80%
探索新知
(2)由这张次数和频率表可知,机器人抛掷完9 999次时,
得到________次正面,正面出现的频率约是_______.
那么,也就是说机器人抛掷完9 999次时,得到_________
次反面,反面出现的频率约是________.
50.1%
5006
4 993
49.9%
探索新知
利用表中给出的数据进行分析、计算.
(1)抛掷5次,正面次数为1,那么反面次数就是4,
出现反面的频率为 =80%,
也可以用1-20%=80%计算.
(2)抛掷完9 999次,得到5 006次正面,
正面出现的频率约为50.1%,
得到反面就是9 999-5 006=4 993(次),
反面出现的频率约为1-50.1%=49.9%.
导引:
典题精讲
1 小胡将一枚质地均匀的硬币抛掷了10次,正面朝上的情况出现了6次,若用A 表示正面朝上这一事件,则事件A 发生的( )
A.频率是0.4
B.频率是0.6
C.频率是6
D.频率接近0.6
B
典题精讲
2 小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
则通话时间不超过15 min的频率为( )
A.0.1 B.0.4
C.0.5 D.0.9
通话时间 x/min 0<x≤ 5 5<x≤ 10 10<x≤ 15 15<x≤ 20
频数 (通话次数) 20 16 9 5
D
典题精讲
3
体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( ) A.16%
B.24%
C.30%
D.40%
D
探索新知
知识点
2
知识点
频率的稳定性
(1)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数n 20 40 80 120 160 200 240 280 320 360 400
钉尖朝上的次数m
钉尖朝上的频率
探索新知
知识点
(2)根据上表,完成图6-1的折线统计图:
(3)观察图6-1的折线统计图,钉尖朝上的频率的变化有什么规律?
探索新知
知识点
在试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
归 纳
探索新知
知识点
例3
在对某次试验数据整理过程中,某个事件出现的频率随试验次数变化的折线图如图,这个图中折线变化的特点是________,试举一个大致符合这个特点的某事件试验的例子(指出关注的结果)________.
探索新知
知识点
随着试验次数的增多,频率逐渐稳定在50%;
在掷硬币的试验当中,正面向上的频率有何变
化?(答案不唯一)
答案:
探索新知
知识点
随机事件发生的频率具有稳定性,试验次数越多,稳定性越明显,频率就越接近于一个常数.
总 结
探索新知
知识点
例4
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
球的颜色 无记号 有记号 红色 黄色 红色 黄色
摸到的次数 18 28 2 2
探索新知
知识点
(1)由题意可知,50次摸球试验中,出现红球20次,
黄球30次,
所以红球占总球数的百分比约为20÷50=40%,
黄球占总球数的百分比约为30÷50=60%.
所以红球约占40%,黄球约占60%.
(2)由题意可知,50次摸球试验中,出现有记号的球
4次,所以总球数约有8÷ =100(个).
所以红球约有100×40%=40(个).
解:
典题精讲
1
(1)完成上表;
某射击运动员在同一条件下进行射击,结果如下表所示:
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 9 16 41 88 168 429 861
击中靶心的频率
0.9
0.8
0.82
0.88
0.84
0.858
0.861
典题精讲
(2)根据上表,画出该运动员击中靶心的频率的折
线统计图;
(3)观察画出的折线统计图,击中靶心的频率的变
化有什么规律
(2)略.
(3)随着射击总次数的增加,击中靶心的频率越来
越接近0.86,且趋于稳定.
解:
典题精讲
2
黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客.某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800 kg.由此估计该果农今年的“优质蓝莓”产量约是________kg.
560
典题精讲
3 某人在做掷硬币试验时,投掷m 次,正面朝上有n 次(即正面朝上的频率是P= ). 则下列说法中正确的是( )
A.P 一定等于
B.P 一定不等于
C.多投一次,P 更接近
D.随投掷次数逐渐增加,P 在 附近摆动
D
典题精讲
4
在一个不透明的盒子里装着若干个白球,小明想估计其中的白球数,于是他放入10个黑球(除颜色外,其他均与白球相同),搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,得到如下数据:
摸球的 次数n 20 40 60 80 120 160 200
摸到白球 的次数m 15 33 49 63 97 128 158
摸到白球 的频率 0.75 0.83 0.82 0.79 0.81 0.80 0.79
估计盒子里白球的个数为( )
A.8 B.40 C.80 D.无法估计
B
5 甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一结果的试验可能是( )
A.掷一枚质地均匀的骰子,
出现1点朝上的频率
B.任意写一个正整数,它
能被3整除的频率
C.抛一枚硬币,出现正面朝上的频率
D.从一个装有2个白球和1个红球的袋子中任取一球,取到白
球的频率
典题精讲
B
学以致用
小试牛刀
1
一个不透明袋子中有1个红球、1个绿球和n 个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n 的值.
小试牛刀
(1)当n=1时,袋中红球数量和白球数量相同,故摸到两种颜色的球的可能性相同.
(2)由题意得0.25= ,
即(2+n )×0.25=1,所以n=2.
解:
小试牛刀
2
为响应习总书记足球进校园的号召,某学校积极开展与足球有关的宣传与实践活动.学生会体育部为了解本校学生对足球运动的态度,随机抽取了部分学生进行调查,并绘制了如下的统计表和如图所示的统计图(部分信息未给出).
态度 频数(人数) 频率
非常喜欢 5 0.05
喜欢 0.35
一般 50 n
不喜欢 10
合计 m 1
小试牛刀
(1)在上面的统计表中m=________,n=________;
(2)请你将条形统计图补充完整;
(3)该校共有学生1 200人,根据统计信息,估计爱好足球运动(包括喜欢和非常喜欢)的学生有多少人?
100
0.5
小试牛刀
(2)“喜欢”的人数=100-5-50-10=35.
所以补充条形统计图如图:
(3)(35+5)÷100×1 200=480(人).
答:估计爱好足球运动的学生有480人.
解:
小试牛刀
3
达州市图书馆4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图所示不完整的统计图表.
八年级(1)班学生去新图书馆的次数统计表
去新图书馆的次数 0次 1次 2次 3次 4次及以上
人数 8 12 a 10 4
请你根据统计图表中的信息,解答下列问题:
(1)填空:a=________,b=________;
16
20
小试牛刀
(2)求扇形统计图中“0次”的扇形所占圆心角的度数;
(3)从全班去过该图书馆的同学中随机抽取1人,谈谈对新图书馆的印象和感受,求恰好抽中去过“4次及以上”的同学的频率.
小试牛刀
(2)扇形统计图中“0次”的扇形所占圆心角的度数
为360°× ×100%=57.6°.
(3)从全班去过该图书馆的同学中随机抽取1人,有50-8=42种结果,其中恰好抽中去过“4次及以上”的同学有4种结果,故恰好抽中去过“4次及以上”的同学的频率为 .
解:
小试牛刀
4
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖与同学们做摸球试验,摸球方法是:将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,累计同学们摸球结果,记录的数据如下表所示:
小试牛刀
(1)把表中的数据补充完整(结果精确到0.01),并根据统计表画出折线统计图;
(2)估计任意摸出一个球是白色的频率(结果精确到0.1).
试验次数 100 200 300 400 500 600 700 800 900 1 000
摸到白球 的次数 70 105 198 235 288 375 408 490 540 599
摸到白球 的频率
小试牛刀
(1)0.70;0.53;0.66;0.59;0.58;0.63;0.58;0.61;0.60;0.60
画出的折线统计图如图所示.
(2)任意摸出一个球是白色的频率约为0.6.
解:
课堂小结
课堂小结
1.频率的定义:在n 次重复试验中,不确定事件A 发生
了m 次,则比值 称为事件A 发生的频率.
2.频率的稳定性:
(1)在大量重复试验的情况下,事件的频率会呈现稳定
性,即频率在一个“常数”附近摆动.随着试验次
数的增加,摆动的幅度将越来越小.
(2)频率是一个比值, 没有单位.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.2频率的稳定性
第1课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
掷一枚图钉,落地后会出现两种情况:
你认为钉尖朝上和钉尖朝下的可能性一样大吗
新课精讲
探索新知
1
知识点
频 率
探索新知
(1)两人一组做20次掷图钉的游戏,并将数据记录在下表中:
试验总次数
钉尖朝上的次数
钉尖朝下的次数
钉尖朝上的频率
钉尖朝下的频率
探索新知
定义:在n 次重复试验中,不确定事件A 发生了m 次,则比值 称为事件A 发生的频率.
探索新知
例1
在一个不透明的盒子中装有n 个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n 大约是________.
10
探索新知
例2
表中是一个机器人做9 999次“抛硬币”游戏时记录下的出现正面的次数和频率.
抛掷次数 5 50 300 800 3 200 6 000 9 999
出现正面 的次数 1 31 135 408 1 508 2 980 5 006
出现正面 的频率 20% 62% 45% 51% 47.1% 49.7% 50.1%
(1)由这张次数和频率表可知,机器人抛掷完5次时,
得到1次正面,正面出现的频率是20%,那么,也
就是说机器人抛掷完5次时,得到______次反面,
反面出现的频率是________.
4
80%
探索新知
(2)由这张次数和频率表可知,机器人抛掷完9 999次时,
得到________次正面,正面出现的频率约是_______.
那么,也就是说机器人抛掷完9 999次时,得到_________
次反面,反面出现的频率约是________.
50.1%
5006
4 993
49.9%
探索新知
利用表中给出的数据进行分析、计算.
(1)抛掷5次,正面次数为1,那么反面次数就是4,
出现反面的频率为 =80%,
也可以用1-20%=80%计算.
(2)抛掷完9 999次,得到5 006次正面,
正面出现的频率约为50.1%,
得到反面就是9 999-5 006=4 993(次),
反面出现的频率约为1-50.1%=49.9%.
导引:
典题精讲
1 小胡将一枚质地均匀的硬币抛掷了10次,正面朝上的情况出现了6次,若用A 表示正面朝上这一事件,则事件A 发生的( )
A.频率是0.4
B.频率是0.6
C.频率是6
D.频率接近0.6
B
典题精讲
2 小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
则通话时间不超过15 min的频率为( )
A.0.1 B.0.4
C.0.5 D.0.9
通话时间 x/min 0<x≤ 5 5<x≤ 10 10<x≤ 15 15<x≤ 20
频数 (通话次数) 20 16 9 5
D
典题精讲
3
体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( ) A.16%
B.24%
C.30%
D.40%
D
探索新知
知识点
2
知识点
频率的稳定性
(1)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数n 20 40 80 120 160 200 240 280 320 360 400
钉尖朝上的次数m
钉尖朝上的频率
探索新知
知识点
(2)根据上表,完成图6-1的折线统计图:
(3)观察图6-1的折线统计图,钉尖朝上的频率的变化有什么规律?
探索新知
知识点
在试验次数很大时,钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
归 纳
探索新知
知识点
例3
在对某次试验数据整理过程中,某个事件出现的频率随试验次数变化的折线图如图,这个图中折线变化的特点是________,试举一个大致符合这个特点的某事件试验的例子(指出关注的结果)________.
探索新知
知识点
随着试验次数的增多,频率逐渐稳定在50%;
在掷硬币的试验当中,正面向上的频率有何变
化?(答案不唯一)
答案:
探索新知
知识点
随机事件发生的频率具有稳定性,试验次数越多,稳定性越明显,频率就越接近于一个常数.
总 结
探索新知
知识点
例4
研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球.怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球试验.摸球试验的要求:先搅拌均匀,每次随机摸出一个球,放回盒中,再继续.
活动结果:摸球试验一共做了50次,统计结果如下表:
推测计算.由上述的摸球试验可推算:
(1)盒中红球、黄球各占总球数的百分比是多少?
(2)盒中有红球多少个?
球的颜色 无记号 有记号 红色 黄色 红色 黄色
摸到的次数 18 28 2 2
探索新知
知识点
(1)由题意可知,50次摸球试验中,出现红球20次,
黄球30次,
所以红球占总球数的百分比约为20÷50=40%,
黄球占总球数的百分比约为30÷50=60%.
所以红球约占40%,黄球约占60%.
(2)由题意可知,50次摸球试验中,出现有记号的球
4次,所以总球数约有8÷ =100(个).
所以红球约有100×40%=40(个).
解:
典题精讲
1
(1)完成上表;
某射击运动员在同一条件下进行射击,结果如下表所示:
射击总次数n 10 20 50 100 200 500 1000
击中靶心的次数m 9 16 41 88 168 429 861
击中靶心的频率
0.9
0.8
0.82
0.88
0.84
0.858
0.861
典题精讲
(2)根据上表,画出该运动员击中靶心的频率的折
线统计图;
(3)观察画出的折线统计图,击中靶心的频率的变
化有什么规律
(2)略.
(3)随着射击总次数的增加,击中靶心的频率越来
越接近0.86,且趋于稳定.
解:
典题精讲
2
黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客.某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800 kg.由此估计该果农今年的“优质蓝莓”产量约是________kg.
560
典题精讲
3 某人在做掷硬币试验时,投掷m 次,正面朝上有n 次(即正面朝上的频率是P= ). 则下列说法中正确的是( )
A.P 一定等于
B.P 一定不等于
C.多投一次,P 更接近
D.随投掷次数逐渐增加,P 在 附近摆动
D
典题精讲
4
在一个不透明的盒子里装着若干个白球,小明想估计其中的白球数,于是他放入10个黑球(除颜色外,其他均与白球相同),搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,得到如下数据:
摸球的 次数n 20 40 60 80 120 160 200
摸到白球 的次数m 15 33 49 63 97 128 158
摸到白球 的频率 0.75 0.83 0.82 0.79 0.81 0.80 0.79
估计盒子里白球的个数为( )
A.8 B.40 C.80 D.无法估计
B
5 甲、乙两名同学在一次大量重复试验中,统计了某一结果出现的频率,绘制出的统计图如图所示,符合这一结果的试验可能是( )
A.掷一枚质地均匀的骰子,
出现1点朝上的频率
B.任意写一个正整数,它
能被3整除的频率
C.抛一枚硬币,出现正面朝上的频率
D.从一个装有2个白球和1个红球的袋子中任取一球,取到白
球的频率
典题精讲
B
学以致用
小试牛刀
1
一个不透明袋子中有1个红球、1个绿球和n 个白球,这些球除颜色外无其他差别.
(1)当n=1时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该试验,发现摸到绿球的频率稳定于0.25,求n 的值.
小试牛刀
(1)当n=1时,袋中红球数量和白球数量相同,故摸到两种颜色的球的可能性相同.
(2)由题意得0.25= ,
即(2+n )×0.25=1,所以n=2.
解:
小试牛刀
2
为响应习总书记足球进校园的号召,某学校积极开展与足球有关的宣传与实践活动.学生会体育部为了解本校学生对足球运动的态度,随机抽取了部分学生进行调查,并绘制了如下的统计表和如图所示的统计图(部分信息未给出).
态度 频数(人数) 频率
非常喜欢 5 0.05
喜欢 0.35
一般 50 n
不喜欢 10
合计 m 1
小试牛刀
(1)在上面的统计表中m=________,n=________;
(2)请你将条形统计图补充完整;
(3)该校共有学生1 200人,根据统计信息,估计爱好足球运动(包括喜欢和非常喜欢)的学生有多少人?
100
0.5
小试牛刀
(2)“喜欢”的人数=100-5-50-10=35.
所以补充条形统计图如图:
(3)(35+5)÷100×1 200=480(人).
答:估计爱好足球运动的学生有480人.
解:
小试牛刀
3
达州市图书馆4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图所示不完整的统计图表.
八年级(1)班学生去新图书馆的次数统计表
去新图书馆的次数 0次 1次 2次 3次 4次及以上
人数 8 12 a 10 4
请你根据统计图表中的信息,解答下列问题:
(1)填空:a=________,b=________;
16
20
小试牛刀
(2)求扇形统计图中“0次”的扇形所占圆心角的度数;
(3)从全班去过该图书馆的同学中随机抽取1人,谈谈对新图书馆的印象和感受,求恰好抽中去过“4次及以上”的同学的频率.
小试牛刀
(2)扇形统计图中“0次”的扇形所占圆心角的度数
为360°× ×100%=57.6°.
(3)从全班去过该图书馆的同学中随机抽取1人,有50-8=42种结果,其中恰好抽中去过“4次及以上”的同学有4种结果,故恰好抽中去过“4次及以上”的同学的频率为 .
解:
小试牛刀
4
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖与同学们做摸球试验,摸球方法是:将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,累计同学们摸球结果,记录的数据如下表所示:
小试牛刀
(1)把表中的数据补充完整(结果精确到0.01),并根据统计表画出折线统计图;
(2)估计任意摸出一个球是白色的频率(结果精确到0.1).
试验次数 100 200 300 400 500 600 700 800 900 1 000
摸到白球 的次数 70 105 198 235 288 375 408 490 540 599
摸到白球 的频率
小试牛刀
(1)0.70;0.53;0.66;0.59;0.58;0.63;0.58;0.61;0.60;0.60
画出的折线统计图如图所示.
(2)任意摸出一个球是白色的频率约为0.6.
解:
课堂小结
课堂小结
1.频率的定义:在n 次重复试验中,不确定事件A 发生
了m 次,则比值 称为事件A 发生的频率.
2.频率的稳定性:
(1)在大量重复试验的情况下,事件的频率会呈现稳定
性,即频率在一个“常数”附近摆动.随着试验次
数的增加,摆动的幅度将越来越小.
(2)频率是一个比值, 没有单位.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
