【班海精品】北师大版(新)七下-6.2频率的稳定性 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-6.2频率的稳定性 第二课时【优质课件】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:21:36 | ||
图片预览










文档简介
(共46张PPT)
6.2频率的稳定性
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
你认为正面朝上和正面朝下的可能性相同吗?
新课精讲
探索新知
1
知识点
概 率
做一做
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
探索新知
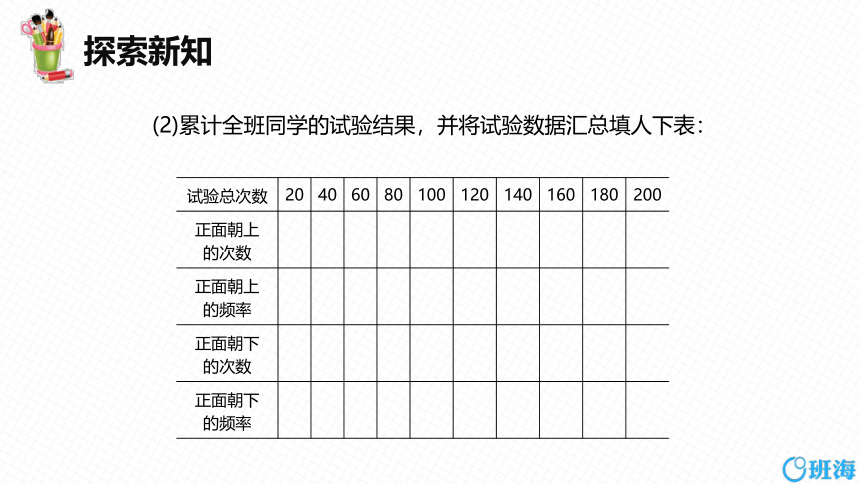
(2)累计全班同学的试验结果,并将试验数据汇总填人下表:
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上 的次数
正面朝上 的频率
正面朝下 的次数
正面朝下 的频率
探索新知
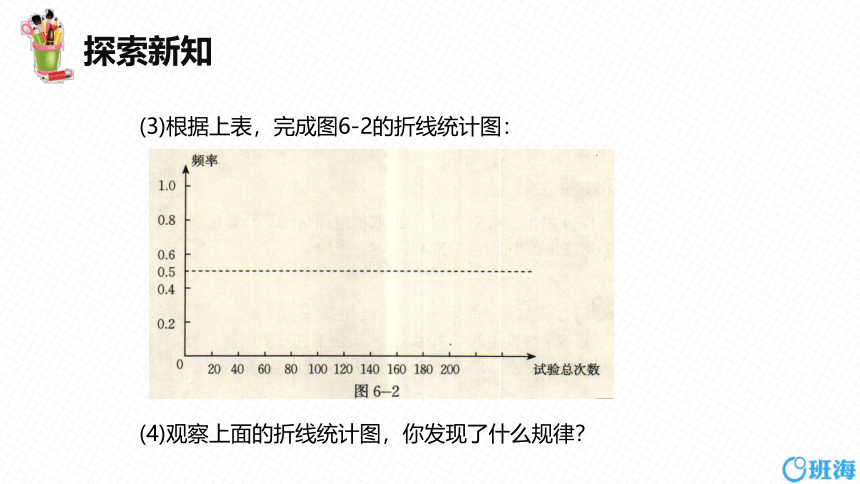
(3)根据上表,完成图6-2的折线统计图:
(4)观察上面的折线统计图,你发现了什么规律?
探索新知
(5)下表列出了一些历史上的数学家所做的掷硬币试验的数据:
试验者 试验总 次数n 正面朝上 的次数m 正面朝上
的频率
布丰 4 040 2 048 0.506 9
德·摩根 4 092 2 048 0.500 5
费勒 10 000 4 979 0.497 9
皮尔逊 12 000 6 019 0.501 6
皮尔逊 24 000 12 012 0.500 5
维尼 30 000 14 994 0.499 8
罗曼诺夫斯基 80 640 39 699 0.492 3
表中的数据支持你发现的规律吗?
探索新知
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A 发生的频率,表示该事件发生的频繁程度,频率越大,事件A 发生越频繁,这就意味着事件A 发生的可能性也越大,因而,我们就用这个常数来表示事件A 发生的可能性的大小.我们把刻画事件A 发生的可能性大小的数值,称为事件A 发生的概率(probability),记为P (A ).
归 纳
探索新知
把刻画事件A 发生的可能性大小的数值,称为事
件A 发生的概率.一般地,大量重复的试验中,我们
常用不确定事件A 发生的频率来估计事件A 发生的概
率,概率是一个理论值,是一个用来刻画事件发生的
可能性大小的量,必然事件发生的概率为1,不可能
事件发生的概率为0,0<不确定事件发生的概率<1.
探索新知
例1
在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色……如此大量摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定在30%.②若从中随机摸出一球,该球是黑球的概率最大.③再摸球100次,必有20次摸出的是红球.其中正确的是( )
A.①②③ B.①②
C.①③ D.②③
B
探索新知
在同一个事件中,几种情况的频率之和等于1,故①
正确;用频率估计概率.可知摸出黑球的概率最大,
故②正确;③概率反映的是可能性的大小,不是绝
对的,故③错误.
导引:
探索新知
例2
一个不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有任何其他区别,将口袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是
(1)估计取出白球的概率是多少?
(2)如果口袋中的白球有18个,那么口袋中的红球约
有多少个?
(1)对于非A 即B 的两个事件,其概率之和为1;
(2)列出方程求解.
导引:
探索新知
(1)因为取出红球的频率是
所以取出红球的概率约是
所以估计取出白球的概率约为1-
(2)设口袋中的红球有x 个,根据题意,得
≈
解得x ≈6.所以口袋中的红球约有6个.
解:
探索新知
(1)对于非A 即B 的两个事件,其概率之和为1;
(2)解答本题运用了方程思想,即根据概率定义列出方程求解.
总 结
典题精讲
1
小凡做了5次掷均匀硬币的试验,其中有3次正面朝上,2次正面朝下,因此他认为正面朝上的概率大约为 ,朝下的概率约为 ,你同意他的观点吗?你认为再多做一些试验,结果还是这样吗?
不同意.试验次数增加到足够多时,结果会发生改变.
解:
典题精讲
2
小明练习射击,共射击600次,其中有380次击中靶子,由此可估计,小明射击一次击中靶子的概率是( )
A.38% B.60%
C.63% D.无法确定
C
典题精讲
3 某收费站在2小时内对经过该站的机动车统计如下表:
若有一辆机动车经过这个收费站,利用上面的统计表估计它是轿车的概率为( )
A. B. C. D.
类型 轿车 货车 客车 其他
数量/辆 36 24 8 12
B
典题精讲
4
下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1
个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有
10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那
么,买这种彩票1 000张,一定会中奖
D.连续掷一枚质地均匀硬币,若5次都是正面朝上,
则第六次仍然可能正面朝上
D
典题精讲
5 下列说法正确的是( )
A.“任意画一个三角形,其内角和为360°”是随机事件
B.已知某篮球运动员投篮投中的概率为0.6,则他投10次可投中6次
C.抽样调查选取样本时,所选样本可按自己的喜好选取
D.检测某城市的空气质量,采用抽样调查法
D
探索新知
知识点
2
知识点
用频率估计概率
频率与概率的联系与区别:
联系:频率和概率是研究不确定事件发生的可能性大小的特征量,当试验次数很大时,可以发现一个不确定事件发生的频率总是在某个常数附近摆动,也就是频率呈现稳定性,随着次数的不断增加,摆动的幅度将会越来越小,在大量的重复试验中,某个事件发生的频率将接近于某个常数,则称此常数为该不确定事件的概率.
区别:频率是变化的,概率是不变的,虽然多次试验的频率逐渐接近于概率,但无论试验多少次,频率仍然是概率的一个近似值,而不能等同于概率.
探索新知
知识点
例3
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他均相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则估计摸到红球的概率是________.
当多次试验后,事件发生的频率会稳定在相应的事件
发生的概率附近,摸到红球的频率稳定在25%附近,
所以估计摸到红球的概率为25%.
导引:
25%
探索新知
知识点
例4
不透明的袋中有4个大小相同的小球,其中2个为白色,1个为红色,1个为绿色,每次从袋中摸出一个球,然后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球次数 1 5 10 15 20 25 30 40 50 60 70 80 90
出现红球的次数 1 2 4 6 9 14 15 17 21 21 22
出现红球的频率 40.0% 32.0%
摸球次数 100 110 120 130 140 150 160 170 180 190 200
出现红球的次数 30 32 36 40 41 45 49 51 54
出现红球的频率 26.0% 25.4%
探索新知
(1)请将表中数据补充完整;
(2)摸球5次和摸球10次所得频率相差多少?25次和30
次之间呢?30次和40次之间,90次和100次之间,
190次和200次之间呢?从中你发现了什么规律?
(3)根据以上数据你能估计红球出现的概率吗?是多少呢?
(4)你能估计白球出现的概率吗?你能估计绿球出现
的概率吗?试一试.
探索新知
知识点
(1)“出现红球的次数”依次填6,8,26,33;
出现红球的频率依次填100.0%,40.0%,40.0%,30.0%,
30.0%,35.0%,30.0%,28.3%,30.0%,26.3%,24.4%,
27.3%,26.7%,25.7%,26.7%,25.6%,26.5%,27.2%,
26.8%,27.0%.
(2)相差分别为0%,2%,5%,1.6%,0.2%;
规律:随着试验次数的增加,红球出现的频率逐渐稳定.
(3)估计红球出现的概率是
(4)估计白球出现的概率是 绿球出现的概率是
解:
典题精讲
1
掷一枚质地均匀的硬币,正面朝上的概率为 ,
那么,掷100次硬币,你能保证恰好50次正面朝上吗?与同伴进行交流.
不能.
解:
典题精讲
2
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
典题精讲
3
一个不透明的盒子里有n 个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n 为( )
A.20 B.24
C.28 D.30
D
典题精讲
4
用频率估计概率时,可以发现:抛掷硬币“正面朝上”的概率为0.5,这是指( )
A.连续掷2次,结果一定是“正面朝上”和“反
面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和
“反面朝上”各50次
C.抛掷2n 次,恰好有n 次“正面朝上”
D.抛掷n 次,当n 越来越大时,正面朝上的频率
会越来越稳定于0.5
D
典题精讲
5
如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
典题精讲
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟试验,则当投掷次数为1 000时,“钉尖向上”的频率一定是0.620. 其中合理的是( )
A.① B.②
C.①② D.①③
B
学以致用
小试牛刀
1
某种玉米种子在相同条件下的发芽试验结果如下表:
(1)计算并完成表格(结果精确到0.01);
(2)请估计,当n 很大时,频率将接近________;
(3)这种玉米种子的发芽概率的估计值是多少?请简要说明理由.
试验的种子粒数n 100 150 200 500 800 1 000
发芽的粒数m 65 111 136 345 560 700
发芽的频率 0.65 0.74 0.68 0.69
0.70
小试牛刀
这种玉米种子的发芽概率的估计值是0.70.
理由:在相同条件下,多次试验,某一事件的发生的频率近似等于概率.
解:
小试牛刀
2
王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n 100 150 200 500 800 1 000
摸到黑球的次数m 23 31 60 130 203 251
摸到黑球的频率 0.23 0.21 0.30 0.26 0.25 _____
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(结果精确到0.01);
(2)估计袋中白球的个数.
0.25
0.25
小试牛刀
(2)设袋中白球为x 个,根据题意得
=0.25,
x=3.
所以估计袋中有3个白球.
解:
小试牛刀
3
在不透明的袋子中有三个大小相同的小球,其中白球2个,红球1个.每次从袋子里摸出一个球,然后放回搅匀再摸,在摸球试验中得到下列部分数据:
(1)请将数据补充完整(结果精确到0.01);
摸球次数 40 80 120 160 200 240 280 320 360 400
出现红 球的次数 14 23 38 52 67 86 97 111 120 133
出现红 球的频率
0.33
0.33
0.33
0.35
0.35
0.35
0.29
0.32
0.34
0.36
小试牛刀
(2)根据表格在图中画出折线统计图;
(3)根据统计表及折线统计图可知:随着摸球次数的增多,出现红球的频率的稳定值是________;
(4)估计出现红球的概率为________.
0.33
0.33
小试牛刀
(2)绘制折线统计图如图所示:
解:
小试牛刀
4
某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上(含100元)就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
小试牛刀
转动转盘的次数n 100 200 400 500 800 1 000
落在“可乐”区域 的次数m 60 122 240 298 604
落在“可乐” 区域的频率 0.60 0.61 0.60 0.59 0.60
(1)计算并完成上述表格;
(2)请估计当n 很大时,频率将会接近________;假如你去转动该转盘一次,你获得“可乐”的概率约是________(结果精确到0.1);
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
472
0.60
0.6
0.6
小试牛刀
(3)由(2)可知落在“车模”区域的概率约是0.4,
从而得到表示“车模”区域的扇形的圆心角的度数约是360°×0.4=144°.
解:
课堂小结
课堂小结
(1)频率是从试验中得出的,而概率是大量重复试验中
某事件发生的频率的结果的归纳,是频率的稳定值.
(2)概率可以看作是频率在理论上的期望值,它在数量
上反映了随机事件发生的可能性的大小,频率在大
量重复试验的前提下可近似地作为这个事件的概率.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
6.2频率的稳定性
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
掷一枚质地均匀的硬币,硬币落下后,会出现两种情况:
你认为正面朝上和正面朝下的可能性相同吗?
新课精讲
探索新知
1
知识点
概 率
做一做
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
探索新知
(2)累计全班同学的试验结果,并将试验数据汇总填人下表:
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上 的次数
正面朝上 的频率
正面朝下 的次数
正面朝下 的频率
探索新知
(3)根据上表,完成图6-2的折线统计图:
(4)观察上面的折线统计图,你发现了什么规律?
探索新知
(5)下表列出了一些历史上的数学家所做的掷硬币试验的数据:
试验者 试验总 次数n 正面朝上 的次数m 正面朝上
的频率
布丰 4 040 2 048 0.506 9
德·摩根 4 092 2 048 0.500 5
费勒 10 000 4 979 0.497 9
皮尔逊 12 000 6 019 0.501 6
皮尔逊 24 000 12 012 0.500 5
维尼 30 000 14 994 0.499 8
罗曼诺夫斯基 80 640 39 699 0.492 3
表中的数据支持你发现的规律吗?
探索新知
无论是掷质地均匀的硬币还是掷图钉,在试验次数很大时正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A 发生的频率,表示该事件发生的频繁程度,频率越大,事件A 发生越频繁,这就意味着事件A 发生的可能性也越大,因而,我们就用这个常数来表示事件A 发生的可能性的大小.我们把刻画事件A 发生的可能性大小的数值,称为事件A 发生的概率(probability),记为P (A ).
归 纳
探索新知
把刻画事件A 发生的可能性大小的数值,称为事
件A 发生的概率.一般地,大量重复的试验中,我们
常用不确定事件A 发生的频率来估计事件A 发生的概
率,概率是一个理论值,是一个用来刻画事件发生的
可能性大小的量,必然事件发生的概率为1,不可能
事件发生的概率为0,0<不确定事件发生的概率<1.
探索新知
例1
在一个不透明的布袋中,红球、黑球、白球共有若干个,除颜色外,形状、大小、质地等完全相同,小新从布袋中随机摸出一球,记下颜色后放回布袋中,摇匀后再随机摸出一球,记下颜色……如此大量摸球试验后,小新发现其中摸出红球的频率稳定于20%,摸出黑球的频率稳定于50%.对此试验,他总结出下列结论:①若进行大量的摸球试验,摸出白球的频率应稳定在30%.②若从中随机摸出一球,该球是黑球的概率最大.③再摸球100次,必有20次摸出的是红球.其中正确的是( )
A.①②③ B.①②
C.①③ D.②③
B
探索新知
在同一个事件中,几种情况的频率之和等于1,故①
正确;用频率估计概率.可知摸出黑球的概率最大,
故②正确;③概率反映的是可能性的大小,不是绝
对的,故③错误.
导引:
探索新知
例2
一个不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有任何其他区别,将口袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是
(1)估计取出白球的概率是多少?
(2)如果口袋中的白球有18个,那么口袋中的红球约
有多少个?
(1)对于非A 即B 的两个事件,其概率之和为1;
(2)列出方程求解.
导引:
探索新知
(1)因为取出红球的频率是
所以取出红球的概率约是
所以估计取出白球的概率约为1-
(2)设口袋中的红球有x 个,根据题意,得
≈
解得x ≈6.所以口袋中的红球约有6个.
解:
探索新知
(1)对于非A 即B 的两个事件,其概率之和为1;
(2)解答本题运用了方程思想,即根据概率定义列出方程求解.
总 结
典题精讲
1
小凡做了5次掷均匀硬币的试验,其中有3次正面朝上,2次正面朝下,因此他认为正面朝上的概率大约为 ,朝下的概率约为 ,你同意他的观点吗?你认为再多做一些试验,结果还是这样吗?
不同意.试验次数增加到足够多时,结果会发生改变.
解:
典题精讲
2
小明练习射击,共射击600次,其中有380次击中靶子,由此可估计,小明射击一次击中靶子的概率是( )
A.38% B.60%
C.63% D.无法确定
C
典题精讲
3 某收费站在2小时内对经过该站的机动车统计如下表:
若有一辆机动车经过这个收费站,利用上面的统计表估计它是轿车的概率为( )
A. B. C. D.
类型 轿车 货车 客车 其他
数量/辆 36 24 8 12
B
典题精讲
4
下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1
个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有
10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那
么,买这种彩票1 000张,一定会中奖
D.连续掷一枚质地均匀硬币,若5次都是正面朝上,
则第六次仍然可能正面朝上
D
典题精讲
5 下列说法正确的是( )
A.“任意画一个三角形,其内角和为360°”是随机事件
B.已知某篮球运动员投篮投中的概率为0.6,则他投10次可投中6次
C.抽样调查选取样本时,所选样本可按自己的喜好选取
D.检测某城市的空气质量,采用抽样调查法
D
探索新知
知识点
2
知识点
用频率估计概率
频率与概率的联系与区别:
联系:频率和概率是研究不确定事件发生的可能性大小的特征量,当试验次数很大时,可以发现一个不确定事件发生的频率总是在某个常数附近摆动,也就是频率呈现稳定性,随着次数的不断增加,摆动的幅度将会越来越小,在大量的重复试验中,某个事件发生的频率将接近于某个常数,则称此常数为该不确定事件的概率.
区别:频率是变化的,概率是不变的,虽然多次试验的频率逐渐接近于概率,但无论试验多少次,频率仍然是概率的一个近似值,而不能等同于概率.
探索新知
知识点
例3
在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他均相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则估计摸到红球的概率是________.
当多次试验后,事件发生的频率会稳定在相应的事件
发生的概率附近,摸到红球的频率稳定在25%附近,
所以估计摸到红球的概率为25%.
导引:
25%
探索新知
知识点
例4
不透明的袋中有4个大小相同的小球,其中2个为白色,1个为红色,1个为绿色,每次从袋中摸出一个球,然后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球次数 1 5 10 15 20 25 30 40 50 60 70 80 90
出现红球的次数 1 2 4 6 9 14 15 17 21 21 22
出现红球的频率 40.0% 32.0%
摸球次数 100 110 120 130 140 150 160 170 180 190 200
出现红球的次数 30 32 36 40 41 45 49 51 54
出现红球的频率 26.0% 25.4%
探索新知
(1)请将表中数据补充完整;
(2)摸球5次和摸球10次所得频率相差多少?25次和30
次之间呢?30次和40次之间,90次和100次之间,
190次和200次之间呢?从中你发现了什么规律?
(3)根据以上数据你能估计红球出现的概率吗?是多少呢?
(4)你能估计白球出现的概率吗?你能估计绿球出现
的概率吗?试一试.
探索新知
知识点
(1)“出现红球的次数”依次填6,8,26,33;
出现红球的频率依次填100.0%,40.0%,40.0%,30.0%,
30.0%,35.0%,30.0%,28.3%,30.0%,26.3%,24.4%,
27.3%,26.7%,25.7%,26.7%,25.6%,26.5%,27.2%,
26.8%,27.0%.
(2)相差分别为0%,2%,5%,1.6%,0.2%;
规律:随着试验次数的增加,红球出现的频率逐渐稳定.
(3)估计红球出现的概率是
(4)估计白球出现的概率是 绿球出现的概率是
解:
典题精讲
1
掷一枚质地均匀的硬币,正面朝上的概率为 ,
那么,掷100次硬币,你能保证恰好50次正面朝上吗?与同伴进行交流.
不能.
解:
典题精讲
2
在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是( )
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
D
典题精讲
3
一个不透明的盒子里有n 个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n 为( )
A.20 B.24
C.28 D.30
D
典题精讲
4
用频率估计概率时,可以发现:抛掷硬币“正面朝上”的概率为0.5,这是指( )
A.连续掷2次,结果一定是“正面朝上”和“反
面朝上”各1次
B.连续抛掷100次,结果一定是“正面朝上”和
“反面朝上”各50次
C.抛掷2n 次,恰好有n 次“正面朝上”
D.抛掷n 次,当n 越来越大时,正面朝上的频率
会越来越稳定于0.5
D
典题精讲
5
如图显示了用计算机模拟随机投掷一枚图钉的某次试验的结果.
典题精讲
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;②随着试验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;③若再次用计算机模拟试验,则当投掷次数为1 000时,“钉尖向上”的频率一定是0.620. 其中合理的是( )
A.① B.②
C.①② D.①③
B
学以致用
小试牛刀
1
某种玉米种子在相同条件下的发芽试验结果如下表:
(1)计算并完成表格(结果精确到0.01);
(2)请估计,当n 很大时,频率将接近________;
(3)这种玉米种子的发芽概率的估计值是多少?请简要说明理由.
试验的种子粒数n 100 150 200 500 800 1 000
发芽的粒数m 65 111 136 345 560 700
发芽的频率 0.65 0.74 0.68 0.69
0.70
小试牛刀
这种玉米种子的发芽概率的估计值是0.70.
理由:在相同条件下,多次试验,某一事件的发生的频率近似等于概率.
解:
小试牛刀
2
王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n 100 150 200 500 800 1 000
摸到黑球的次数m 23 31 60 130 203 251
摸到黑球的频率 0.23 0.21 0.30 0.26 0.25 _____
(1)补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(结果精确到0.01);
(2)估计袋中白球的个数.
0.25
0.25
小试牛刀
(2)设袋中白球为x 个,根据题意得
=0.25,
x=3.
所以估计袋中有3个白球.
解:
小试牛刀
3
在不透明的袋子中有三个大小相同的小球,其中白球2个,红球1个.每次从袋子里摸出一个球,然后放回搅匀再摸,在摸球试验中得到下列部分数据:
(1)请将数据补充完整(结果精确到0.01);
摸球次数 40 80 120 160 200 240 280 320 360 400
出现红 球的次数 14 23 38 52 67 86 97 111 120 133
出现红 球的频率
0.33
0.33
0.33
0.35
0.35
0.35
0.29
0.32
0.34
0.36
小试牛刀
(2)根据表格在图中画出折线统计图;
(3)根据统计表及折线统计图可知:随着摸球次数的增多,出现红球的频率的稳定值是________;
(4)估计出现红球的概率为________.
0.33
0.33
小试牛刀
(2)绘制折线统计图如图所示:
解:
小试牛刀
4
某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上(含100元)就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
小试牛刀
转动转盘的次数n 100 200 400 500 800 1 000
落在“可乐”区域 的次数m 60 122 240 298 604
落在“可乐” 区域的频率 0.60 0.61 0.60 0.59 0.60
(1)计算并完成上述表格;
(2)请估计当n 很大时,频率将会接近________;假如你去转动该转盘一次,你获得“可乐”的概率约是________(结果精确到0.1);
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
472
0.60
0.6
0.6
小试牛刀
(3)由(2)可知落在“车模”区域的概率约是0.4,
从而得到表示“车模”区域的扇形的圆心角的度数约是360°×0.4=144°.
解:
课堂小结
课堂小结
(1)频率是从试验中得出的,而概率是大量重复试验中
某事件发生的频率的结果的归纳,是频率的稳定值.
(2)概率可以看作是频率在理论上的期望值,它在数量
上反映了随机事件发生的可能性的大小,频率在大
量重复试验的前提下可近似地作为这个事件的概率.
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
