【班海精品】北师大版(新)七下-3.3用图象表示的变量间关系 【优质教案】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-3.3用图象表示的变量间关系 【优质教案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 443.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览




文档简介
班海数学精批——一本可精细批改的教辅
3.3用图象表示的变量间关系
曲线型图象表示变量之间的关系
教材与学情分析
1、本节教材"温度的变化"从学生所熟悉的情境人手,从图像中获取两变量之间的关系的信息,经历从数学的角度体会变量和变量之间相互依赖的关系,体会图像在表达两变量间变化关系的直观性,感受数学的应用价值。本节教材能使学生初步感受函数思想,能更好地发展学生有条理地进行思考和表达的能力,为以后顺利过渡到函数学习打下基础。
2、学生通过观察现实生活,对用图像来反映两变量之间的关系有了一定的体验,积累有了一些生活的经验;具有初步的搜集信息的能力。通过本节的学习,培养了学生的观察能力、思维表达能力等。
教学目标
知识与技能目标:
1、了解两个变量之间的对应关系,初步形成函数的思想.
2、结合具体情境理解图象上的点所表示的意义.
3、发展从图象中获得信息的能力及有条理地进行语言表达的能力.
4、理解用数学的方法描述变量之间的关系,感受数学的价值.
过程与方法目标:经历从图象中分析变量之间的关系的过程,进一步体会变量之间的关系,在具体情境中培养学生对变量之间关系的认识和语言描述的合理性,培养学生从图象中获取信息的广泛性和准确性.
情感与态度目标:从解决大量实际问题和学生感兴趣的问题中提高学生用数学的意识,体验数学所蕴含的数学美.
教学重点
把实际问题转化为数学图像,再根据图像来研究实际问题,使学生获得对图象反映变量之间关系的体验.
教学难点
从图像中获得一些信息与在现实情景下用语言进行描述之间的等价转化;用图像法来反映两变量之间关系,解决自己身边的一些实际问题,根据图像的特点来研究实际问题.
教学过程设计:
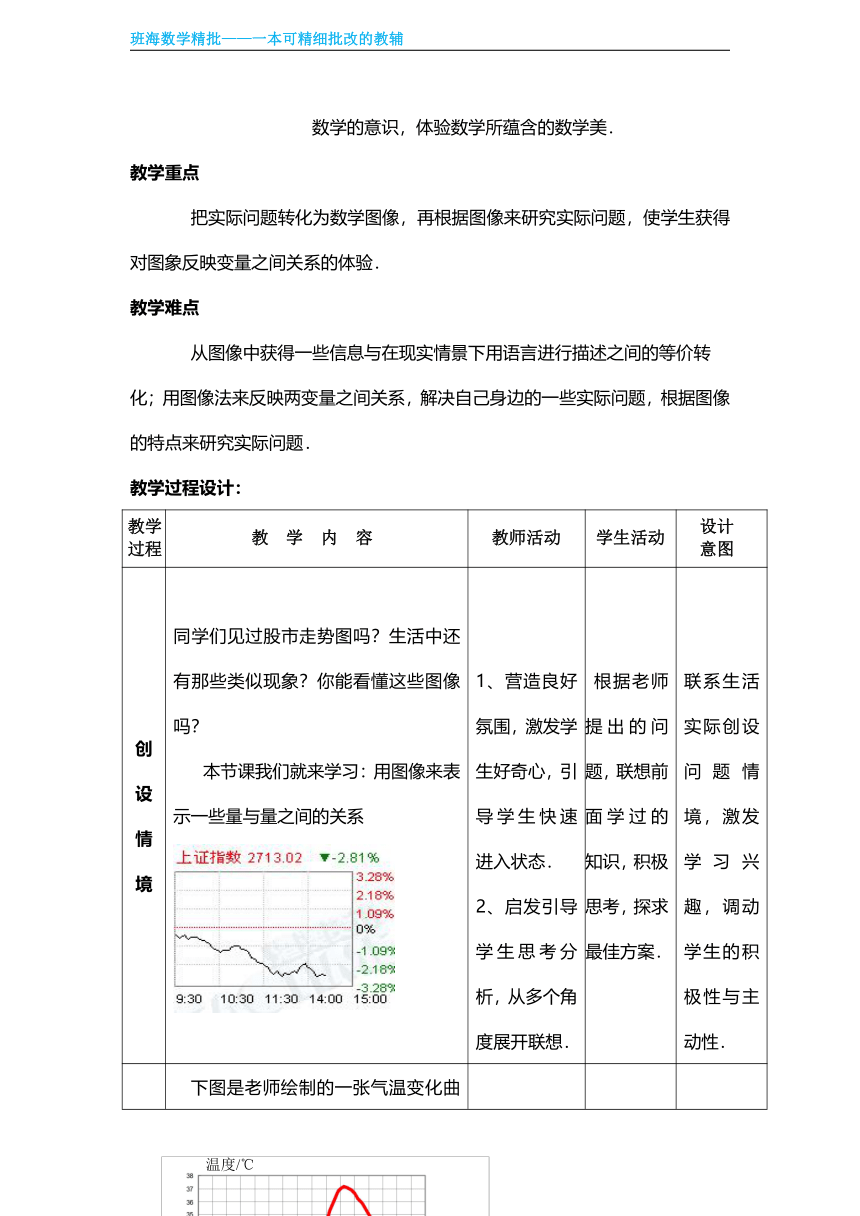
创设情境 同学们见过股市走势图吗?生活中还有那些类似现象?你能看懂这些图像吗?本节课我们就来学习:用图像来表示一些量与量之间的关系 1、营造良好氛围,激发学生好奇心,引导学生快速进入状态.2、启发引导学生思考分析,从多个角度展开联想. 根据老师提出的问题,联想前面学过的知识,积极思考,探求最佳方案. 联系生活实际创设问题情境,激发学习兴趣,调动学生的积极性与主动性.
发现探究 下图是老师绘制的一张气温变化曲线图,直观形象地表达了温度随时间的变化而变化的情况,你能根据下图回答下列问题吗?(1)上午9时的温度是多少?12时呢?(2)这一天的最高温度是多少?是在几时达到的?最低温度呢?(3)这一天的温差是多少?从最低温度到最高温度经过了多少时间?(4)在什么时间范围内温度在上升?在什么时间范围内温度在下降?(5)图中的A点表示的是什么?B点呢? 1、让学生展示自己的分析过程.2、引导学生将新旧知识联系起来,发现新问题,利用所学知识解决新问题,引导学生进行自主探究,获得新知. 1、学生根据自己的生活经验积极寻求最佳表述方式.2、学生展示自己的分析与解决过程.3、在老师的引导下分组讨论.4、与同桌进行交流.5、总结. 通过对层层推进的问题串的形式逐步引导学生获得图象所传达的信息,熟悉图象语言,培养学生自主探索的意识和能力,使学生在探索的过程中形成自己的观点,让学生体会成功的喜悦.
发散探究 就上述温度随时间变化而变化的图象特征,请同学们再想一想,我们还可以得出哪些看法?变量之间的关系还可以怎样表示?(学生分组讨论)教师小结:图象是我们表示变量之间关系的又一种方法,它的特点是非常直观。 在用图象表示变量之间关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量。 巡视各组讨论情况,并参与一些小组的讨论,组织学生交流,鼓励创新的见解. 根据老师所提问题,先独立思考,然后小组交流讨论,并派代表发言. 设计、观察、讨论、交流等有效的活动是学习数学的重要方式.
迁移创新 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.1.一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?2.从16时到24时,骆驼的体温下降了多少?3.在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?4.你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其他时刻呢?5.A点表示的是什么?还有几时的温度与A点所表示的温度相同? 1、多媒体展示.2、巡视、点拨.3、评价、分析、总结学生的解题方法. 1、在老师的引导下积极思考并回答问题.2、学生独立思考,自主解答.3、小组内交流、讨论. 通过对骆驼体温变化这一有趣问题的讨论,学生进一步学习根据图象大致分析变量之间的关系.培养学生迁移创新的意识与能力.
实践操作 海水受太阳和月亮的引力而产生潮汐现象,早晨海水上涨的现象叫做潮,黄昏上涨叫做汐,合称潮汐.下图是某港口从0时到12时的水深情况. 请每位同学根据这个图表自己设计一个问题,再在小组内每人充当一次小老师,请其他同学回答. 根据前面的经验,学会设计问题串,提出尽量多的问题,分组讨论,互问互答. 以研究人员的身分对图象进行分析,主动提出问题,培养学生发现问题、分析问题的能力.
小结与反思 通过本节课的学习与交流,你有什么新的收获与体会?愿意与全班同学交流吗?本节课从图象中分析了两个变量之间的关系,结合温度变化直观而形象地从图中获得了变量之间的有关信息,用图象来直观地反映变量之间的关系是表格法、关系式法所无法代替的. 引导学生进行小结与反思,体会数学在生活的用途,明白生活中处处有数学,建立应用数学的意识. 在学习内容、方式及分析图象的技巧上谈个人的收获,再一次体会探究数学问题的乐趣. 培养学生分析、归纳和总结问题的能力;并起到画龙点睛的作用.
练习反馈 某市一周平均气温(℃)如图所示, 2、 在夏天一杯开水放在桌面上,其水温T下列说法不正确的是( ) 与放置时间 t 的关系大致图象为( )星期二的平均气温最高; 星期四到星期日天气逐渐转暖;这一周最高气温与最低气温相差4℃; 星期四的平均气温最低.
实践研究 1、你能从图中获得哪些信息?2、你能预测5月7日的旅游人数吗 3、你会选择这7天中的哪一天出游?
作业设计板书设计 习题12.3课题变量的表示方法3:图像法在用图象表示变量之间关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量。
折线型图象表示的变量间关系
1.理解分段图象的意义,掌握分段图象各个部分的含义;
2.复习巩固运用图象表示变量间关系的方法,能够运用其解决实际问题.(重点,难点)
一、情境导入
小强和爷爷经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分钟)的关系(从小强开始爬山时计时).
问:图中的横轴(x轴)和纵轴(y轴)各表示什么?
答:横轴(x轴)表示两人爬山所用时间,纵轴(y轴)表示两人离开山脚的距离.
问:如图,线段上有一点P,则P的坐标是多少?表示的实际意义是什么?
答:P的坐标是(3,90).表示小强爬山3分钟时,离开山脚的距离是90米.
我们能否从图象中看出其他信息呢?
二、合作探究
探究点:用折线型图象表示变量间关系
【类型一】用折线型图象表示两个变量间的关系
小明放学后从学校乘轻轨回家,他从学校出发,先匀速步行至轻轨车站,等了一会儿,小明搭轻轨回到家,下面能反映在此过程中小明与家的距离y与时间x的关系的大致图象是( )
解析:根据从学校回家,可得与家的距离是越来越近.根据步行的速度慢,可得离家的距离变化小,根据搭轻轨的速度快,可得离家的距离变化大.A.随着时间的变化,离家的距离越来越远,故A、B错误;C.随着时间的变化,步行离家的距离变化快,搭轻轨的距离变化慢,不符合题意,故C错误;D.随着时间的变化,步行离家的距离变化慢,搭轻轨的距离变化快,符合题意,故D正确.故选D.
方法总结:路程问题中,在不同的时间内,速度可以发生变化,要掌握这类问题,就要对图像中各个线段的意义正确理解.
变式训练:见《学练优》本课时练习“课堂达标训练”第1题
【类型二】利用折线型图象解决图形问题
用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为折线),这个容器的形状是图中( )
解析:由图象可得容器形状不是粗细均匀的物体.相比较而言,前一个阶段,用时较多,高度增加较慢,那么下面的物体应较粗.故选C.
变式训练:见《学练优》本课时练习“课堂达标训练”第2题
【类型三】通过折线型图象获取信息
星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速是多少?
(4)玲玲全程骑车的平均速度是多少?
解析:(1)利用图中的点的横坐标表示时间,纵坐标表示离家的距离,进而得出答案;(2)休息是路程不随时间的增加而增加;(3)用距离除以所用时间求出速度,再比较大小即可;(4)用玲玲全程所行的路程除以所用的时间即可.
解:观察图象可知:(1)玲玲到离家最远的地方需要3小时,此时离家30千米;
(2)10点半时开始第一次休息,休息了半小时;
(3)玲玲郊游过程中,各时间段的速度分别为:9时~10时,速度为10÷(10-9)=10(千米/时);10时~10时30分,速度约为(17.5-10)÷(10.5-10)=(15千米/时);10时30分~11时,速度为0;11时~12时,速度为(30-17.5)÷(12-11)=12.5(千米/时);12时~13时,速度为0;13时~15时,在返回的途中,速度为30÷(15-13)=15(千米/时);可见骑行最快有两段时间:10时~10时30分;13时~15时.两段时间的速度都是15千米/时;
(4)玲玲全程骑车的平均速度为(30+30)÷(15-9)=10(千米/时).
答:玲玲全程骑车的平均速度是10千米/时. 方法总结:准确理解图象上的点所表示的意义是解决问题的关键,解题时可通过仔细观察图象,从中整理出解题时所需的相关信息.
变式训练:见《学练优》本课时练习“课堂达标训练”第4题
【类型四】双图象问题
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的图象如图所示,请你根据图象,回答下列问题:
(1)这次龙舟赛的全程是多少米?哪队先到达终点?
(2)求乙与甲相遇时乙的速度.
解析:(1)根据图象的纵坐标,可得比赛的路程.根据图象的横坐标,可得比赛的结果;(2)根据乙加速后行驶的路程除以加速后的时间,可得答案.
解:(1)由纵坐标看出,这次龙舟赛的全程是1000米;由横坐标看出,乙队先到达终点;
(2)由图象看出,相遇是在乙加速后,加速后的路程是1000-400=600(米),加速后用的时间是3.8-2.2=1.6(分钟),乙与甲相遇时乙的速度600÷1.6=375(米/分钟).
方法总结:解决双图象问题时,正确识别图象,弄清楚两图象所代表的意义,从中挖掘有用的信息,明确实际意义.
课后训练:
三、板书设计
1.用折线型图象表示变量间关系
2.根据折线型图象获取信息解决问题
经历一般规律的探索过程,培养学生的抽象思维能力,经历从实际问题中得到关系式这一过程,提升学生的数学应用能力,使学生在探索过程中体验成功的喜悦,树立学习的自信心.体验生活中数学的应用价值,感受数学与人类生活的密切联系,激发学生学数学、用数学的兴趣
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
教学
过程
教 学 内 容
教师活动
学生活动
设计
意图
温度/℃
A
B
时间/时
水深/米
时间/时
2.2
2.0
1.0
1.2
1.4
1.6
1.8
0
1
2
3
4
5
6
7
时间/天
人数/万
5月1日至5月6日柘林湖旅游人数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
3.3用图象表示的变量间关系
曲线型图象表示变量之间的关系
教材与学情分析
1、本节教材"温度的变化"从学生所熟悉的情境人手,从图像中获取两变量之间的关系的信息,经历从数学的角度体会变量和变量之间相互依赖的关系,体会图像在表达两变量间变化关系的直观性,感受数学的应用价值。本节教材能使学生初步感受函数思想,能更好地发展学生有条理地进行思考和表达的能力,为以后顺利过渡到函数学习打下基础。
2、学生通过观察现实生活,对用图像来反映两变量之间的关系有了一定的体验,积累有了一些生活的经验;具有初步的搜集信息的能力。通过本节的学习,培养了学生的观察能力、思维表达能力等。
教学目标
知识与技能目标:
1、了解两个变量之间的对应关系,初步形成函数的思想.
2、结合具体情境理解图象上的点所表示的意义.
3、发展从图象中获得信息的能力及有条理地进行语言表达的能力.
4、理解用数学的方法描述变量之间的关系,感受数学的价值.
过程与方法目标:经历从图象中分析变量之间的关系的过程,进一步体会变量之间的关系,在具体情境中培养学生对变量之间关系的认识和语言描述的合理性,培养学生从图象中获取信息的广泛性和准确性.
情感与态度目标:从解决大量实际问题和学生感兴趣的问题中提高学生用数学的意识,体验数学所蕴含的数学美.
教学重点
把实际问题转化为数学图像,再根据图像来研究实际问题,使学生获得对图象反映变量之间关系的体验.
教学难点
从图像中获得一些信息与在现实情景下用语言进行描述之间的等价转化;用图像法来反映两变量之间关系,解决自己身边的一些实际问题,根据图像的特点来研究实际问题.
教学过程设计:
创设情境 同学们见过股市走势图吗?生活中还有那些类似现象?你能看懂这些图像吗?本节课我们就来学习:用图像来表示一些量与量之间的关系 1、营造良好氛围,激发学生好奇心,引导学生快速进入状态.2、启发引导学生思考分析,从多个角度展开联想. 根据老师提出的问题,联想前面学过的知识,积极思考,探求最佳方案. 联系生活实际创设问题情境,激发学习兴趣,调动学生的积极性与主动性.
发现探究 下图是老师绘制的一张气温变化曲线图,直观形象地表达了温度随时间的变化而变化的情况,你能根据下图回答下列问题吗?(1)上午9时的温度是多少?12时呢?(2)这一天的最高温度是多少?是在几时达到的?最低温度呢?(3)这一天的温差是多少?从最低温度到最高温度经过了多少时间?(4)在什么时间范围内温度在上升?在什么时间范围内温度在下降?(5)图中的A点表示的是什么?B点呢? 1、让学生展示自己的分析过程.2、引导学生将新旧知识联系起来,发现新问题,利用所学知识解决新问题,引导学生进行自主探究,获得新知. 1、学生根据自己的生活经验积极寻求最佳表述方式.2、学生展示自己的分析与解决过程.3、在老师的引导下分组讨论.4、与同桌进行交流.5、总结. 通过对层层推进的问题串的形式逐步引导学生获得图象所传达的信息,熟悉图象语言,培养学生自主探索的意识和能力,使学生在探索的过程中形成自己的观点,让学生体会成功的喜悦.
发散探究 就上述温度随时间变化而变化的图象特征,请同学们再想一想,我们还可以得出哪些看法?变量之间的关系还可以怎样表示?(学生分组讨论)教师小结:图象是我们表示变量之间关系的又一种方法,它的特点是非常直观。 在用图象表示变量之间关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量。 巡视各组讨论情况,并参与一些小组的讨论,组织学生交流,鼓励创新的见解. 根据老师所提问题,先独立思考,然后小组交流讨论,并派代表发言. 设计、观察、讨论、交流等有效的活动是学习数学的重要方式.
迁移创新 骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大的变化.1.一天中,骆驼体温的变化范围是什么?它的体温从最低上升到最高需要多少时间?2.从16时到24时,骆驼的体温下降了多少?3.在什么时间范围内骆驼的体温在上升?在什么时间范围内骆驼的体温在下降?4.你能看出第二天8时骆驼的体温与第一天8时有什么关系吗?其他时刻呢?5.A点表示的是什么?还有几时的温度与A点所表示的温度相同? 1、多媒体展示.2、巡视、点拨.3、评价、分析、总结学生的解题方法. 1、在老师的引导下积极思考并回答问题.2、学生独立思考,自主解答.3、小组内交流、讨论. 通过对骆驼体温变化这一有趣问题的讨论,学生进一步学习根据图象大致分析变量之间的关系.培养学生迁移创新的意识与能力.
实践操作 海水受太阳和月亮的引力而产生潮汐现象,早晨海水上涨的现象叫做潮,黄昏上涨叫做汐,合称潮汐.下图是某港口从0时到12时的水深情况. 请每位同学根据这个图表自己设计一个问题,再在小组内每人充当一次小老师,请其他同学回答. 根据前面的经验,学会设计问题串,提出尽量多的问题,分组讨论,互问互答. 以研究人员的身分对图象进行分析,主动提出问题,培养学生发现问题、分析问题的能力.
小结与反思 通过本节课的学习与交流,你有什么新的收获与体会?愿意与全班同学交流吗?本节课从图象中分析了两个变量之间的关系,结合温度变化直观而形象地从图中获得了变量之间的有关信息,用图象来直观地反映变量之间的关系是表格法、关系式法所无法代替的. 引导学生进行小结与反思,体会数学在生活的用途,明白生活中处处有数学,建立应用数学的意识. 在学习内容、方式及分析图象的技巧上谈个人的收获,再一次体会探究数学问题的乐趣. 培养学生分析、归纳和总结问题的能力;并起到画龙点睛的作用.
练习反馈 某市一周平均气温(℃)如图所示, 2、 在夏天一杯开水放在桌面上,其水温T下列说法不正确的是( ) 与放置时间 t 的关系大致图象为( )星期二的平均气温最高; 星期四到星期日天气逐渐转暖;这一周最高气温与最低气温相差4℃; 星期四的平均气温最低.
实践研究 1、你能从图中获得哪些信息?2、你能预测5月7日的旅游人数吗 3、你会选择这7天中的哪一天出游?
作业设计板书设计 习题12.3课题变量的表示方法3:图像法在用图象表示变量之间关系时,通常用水平方向的数轴(称为横轴)上的点表示自变量,用竖直方向的数轴(称为纵轴)上的点表示因变量。
折线型图象表示的变量间关系
1.理解分段图象的意义,掌握分段图象各个部分的含义;
2.复习巩固运用图象表示变量间关系的方法,能够运用其解决实际问题.(重点,难点)
一、情境导入
小强和爷爷经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分钟)的关系(从小强开始爬山时计时).
问:图中的横轴(x轴)和纵轴(y轴)各表示什么?
答:横轴(x轴)表示两人爬山所用时间,纵轴(y轴)表示两人离开山脚的距离.
问:如图,线段上有一点P,则P的坐标是多少?表示的实际意义是什么?
答:P的坐标是(3,90).表示小强爬山3分钟时,离开山脚的距离是90米.
我们能否从图象中看出其他信息呢?
二、合作探究
探究点:用折线型图象表示变量间关系
【类型一】用折线型图象表示两个变量间的关系
小明放学后从学校乘轻轨回家,他从学校出发,先匀速步行至轻轨车站,等了一会儿,小明搭轻轨回到家,下面能反映在此过程中小明与家的距离y与时间x的关系的大致图象是( )
解析:根据从学校回家,可得与家的距离是越来越近.根据步行的速度慢,可得离家的距离变化小,根据搭轻轨的速度快,可得离家的距离变化大.A.随着时间的变化,离家的距离越来越远,故A、B错误;C.随着时间的变化,步行离家的距离变化快,搭轻轨的距离变化慢,不符合题意,故C错误;D.随着时间的变化,步行离家的距离变化慢,搭轻轨的距离变化快,符合题意,故D正确.故选D.
方法总结:路程问题中,在不同的时间内,速度可以发生变化,要掌握这类问题,就要对图像中各个线段的意义正确理解.
变式训练:见《学练优》本课时练习“课堂达标训练”第1题
【类型二】利用折线型图象解决图形问题
用均匀的速度向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OAB为折线),这个容器的形状是图中( )
解析:由图象可得容器形状不是粗细均匀的物体.相比较而言,前一个阶段,用时较多,高度增加较慢,那么下面的物体应较粗.故选C.
变式训练:见《学练优》本课时练习“课堂达标训练”第2题
【类型三】通过折线型图象获取信息
星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题.
(1)玲玲到达离家最远的地方是什么时间?离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)她骑车速度最快是在什么时候?车速是多少?
(4)玲玲全程骑车的平均速度是多少?
解析:(1)利用图中的点的横坐标表示时间,纵坐标表示离家的距离,进而得出答案;(2)休息是路程不随时间的增加而增加;(3)用距离除以所用时间求出速度,再比较大小即可;(4)用玲玲全程所行的路程除以所用的时间即可.
解:观察图象可知:(1)玲玲到离家最远的地方需要3小时,此时离家30千米;
(2)10点半时开始第一次休息,休息了半小时;
(3)玲玲郊游过程中,各时间段的速度分别为:9时~10时,速度为10÷(10-9)=10(千米/时);10时~10时30分,速度约为(17.5-10)÷(10.5-10)=(15千米/时);10时30分~11时,速度为0;11时~12时,速度为(30-17.5)÷(12-11)=12.5(千米/时);12时~13时,速度为0;13时~15时,在返回的途中,速度为30÷(15-13)=15(千米/时);可见骑行最快有两段时间:10时~10时30分;13时~15时.两段时间的速度都是15千米/时;
(4)玲玲全程骑车的平均速度为(30+30)÷(15-9)=10(千米/时).
答:玲玲全程骑车的平均速度是10千米/时. 方法总结:准确理解图象上的点所表示的意义是解决问题的关键,解题时可通过仔细观察图象,从中整理出解题时所需的相关信息.
变式训练:见《学练优》本课时练习“课堂达标训练”第4题
【类型四】双图象问题
端午节至,甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程s(米)与时间t(分钟)之间的图象如图所示,请你根据图象,回答下列问题:
(1)这次龙舟赛的全程是多少米?哪队先到达终点?
(2)求乙与甲相遇时乙的速度.
解析:(1)根据图象的纵坐标,可得比赛的路程.根据图象的横坐标,可得比赛的结果;(2)根据乙加速后行驶的路程除以加速后的时间,可得答案.
解:(1)由纵坐标看出,这次龙舟赛的全程是1000米;由横坐标看出,乙队先到达终点;
(2)由图象看出,相遇是在乙加速后,加速后的路程是1000-400=600(米),加速后用的时间是3.8-2.2=1.6(分钟),乙与甲相遇时乙的速度600÷1.6=375(米/分钟).
方法总结:解决双图象问题时,正确识别图象,弄清楚两图象所代表的意义,从中挖掘有用的信息,明确实际意义.
课后训练:
三、板书设计
1.用折线型图象表示变量间关系
2.根据折线型图象获取信息解决问题
经历一般规律的探索过程,培养学生的抽象思维能力,经历从实际问题中得到关系式这一过程,提升学生的数学应用能力,使学生在探索过程中体验成功的喜悦,树立学习的自信心.体验生活中数学的应用价值,感受数学与人类生活的密切联系,激发学生学数学、用数学的兴趣
感谢您下载使用【班海】教学资源。班海——老师们都在免费用的数学作业精细批改微信小程序!
教学
过程
教 学 内 容
教师活动
学生活动
设计
意图
温度/℃
A
B
时间/时
水深/米
时间/时
2.2
2.0
1.0
1.2
1.4
1.6
1.8
0
1
2
3
4
5
6
7
时间/天
人数/万
5月1日至5月6日柘林湖旅游人数
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
