【班海精品】北师大版(新)七下-2.1两条直线的位置关系 第二课时【优质课件】
文档属性
| 名称 | 【班海精品】北师大版(新)七下-2.1两条直线的位置关系 第二课时【优质课件】 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 10:21:36 | ||
图片预览











文档简介
(共49张PPT)
2.1两条直线的
位置关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平面内,两条直线有哪些位置关系?
复
习
回
顾
新课精讲
探索新知
1
知识点
垂直的定义
观察思考
当转动一木条的位置时,什么也随着发生了变化?
探索新知
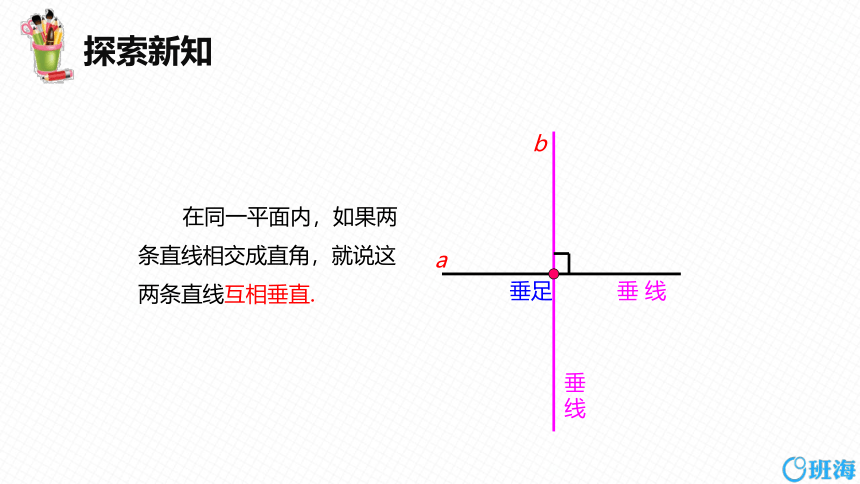
a
b
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂 线
垂
线
探索新知
定义:在两条直线AB 和CD 相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直;记作“AB⊥CD ”,读作“AB 垂直于CD ”;其中一条直线叫做另一条直线的垂线,它们的交点O 叫做垂足.如图.
探索新知
导引:要判断OE,OF 是什么位置关系,其实质是说明OE,OF 是否垂直,即要看∠EOF 是否为90°;要让∠EOF=90°,需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,这样就把问题转化为说明∠AOE=∠COF (已知)了.
例1 如图,CO⊥AB 于点O,∠AOE=∠COF,则射
线OE,OF 是什么位置关系?请说明理由.
探索新知
解:射线OE,OF 互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE 与OF 互相垂直(垂直定义).
探索新知
总 结
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
典题精讲
1
分别找出下列图中互相垂直的线段.
(1)AO⊥OC,OB⊥OD.
(2)DC⊥BC,DC⊥CE,DC⊥BE;AC⊥BC,
AC⊥CE,AC⊥BE;DA⊥BC,DA⊥CE,
DA⊥BE.
解:
典题精讲
如图,已知点O 在直线AB上,CO⊥DO 于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
2
C
典题精讲
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
3
B
典题精讲
如图,点O 在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB 的大小为( )
A.36°
B.54°
C.55°
D.44°
4
B
典题精讲
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD 的度数是( )
A.117°
B.127°
C.153°
D.163°
5
C
典题精讲
如图,直线AB,CD 相交于点O,射线OM 平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON 的度数为( )
A.35°
B.45°
C.55°
D.65°
6
C
探索新知
2
知识点
垂线的画法
做一做
(1)你能借助三角尺在一张白纸上
画出两条互相垂直的直线吗?
(2)如果只有直尺,你能在右图方格
纸上画出两条互相垂直的直线吗?
(3)你能用折纸的方法折出互相垂直的直线吗?试试看!
探索新知
1.垂线的画法:
经过一点(已知直线上或直线外),画已知直线的垂线,步骤如下:
(1)靠线:让直角三角板的一条直角边与已知直线重合;
(2)过点:沿直线移动,使直角三角板的另一条直角边经过已知点;
(3)画线:沿直角边画线,则这条直线就是经过这个点的已知直线的垂线.如图.
探索新知
例2
如图,M 是三角形ABC 中BC 边上的任意一点,请你按照下列要求画图:
(1)过M 点画直线AB 的垂线m;
(2)过M 点画直线BC 的垂线n;
(3)过M 点画直线AC 的垂线p.
观察图形不难看出,(1)(3)属于过直线外一点画已知
直线的垂线,(2)属于过直线上一点画已知直线的垂线,
所以按照“一靠、二过、三画”的方法画图即可.
导引:
探索新知
画出的直线m,n,p 如图.
解:
探索新知
过已知点画已知直线的垂线,实际上就是过已
知点画一条直线,使所画直线与已知直线相交所成
的角是90°.
总 结
典题精讲
1
画一条直线 l,在直线 l,上取一点A,在直线 l,外取一点B,分别经过点A,B 用三角尺或量角器画直线l 的垂线.
如图.
解:
典题精讲
2
下列选项中,过点P 画AB 的垂线,三角尺放法正确的是( )
C
典题精讲
过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
3
D
探索新知
3
知识点
垂线的性质
想一想
(1)如图,点A 在直线l 上,过点A 画直线l 的垂线,你能
画出多少条?如果点A 在直线l 外呢?
A
l
A
l
探索新知
平面内,过一点有且只有一条直线与已知直线垂直.
归 纳
探索新知
例3 如图,已知直线AB,CB,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
C
探索新知
导引:根据题意可知,过点B 有AB,CB 都与直线l 垂直,
由垂线的性质可知,在同一平面内,过一点有且
只有一条直线与已知直线垂直,所以A、B、C 三
点在一条直线上.
探索新知
总 结
利用直线的性质解答题目,要注意直线性质满足的条件:
1. 在平面内;
2. 过一点,点的位置可以在直线上也可以在直线外;
3. 相交所成的角必须是直角,以上三条缺一不可.
典题精讲
在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
1
C
典题精讲
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON 重合(即O,M,N 三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只
有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有
一条直线与已知直线垂直
D.两点之间,线段最短
2
C
易错提醒
(1)在图①中,过AB 外一点M 作AB 的垂线;
(2)在图②中,过点A,B 分别作OB,OA 的垂线.
易错点:误认为垂足一定要在线段或射线上而导致错误.
易错提醒
解:
(1)如图①所示.
(2)如图②所示.
学以致用
小试牛刀
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个 B.1个 C.2个 D.3个
D
1
小试牛刀
2
在直线AB上任取一点O,过点O 作射线OC,OD,
使OC⊥OD,当∠AOC=30°时,∠BOD 的度数是多少?
小试牛刀
解:
如图①,当OC,OD 在AB 同侧时,
因为OC⊥OD,
所以∠COD=90°.
因为∠AOC=30°,
所以∠BOD=180°-∠COD-∠AOC=60°.
如图②,当OC,OD 在AB 异侧时,
因为OC⊥OD,所以∠COD=90°.
因为∠AOC=30°,所以∠AOD=90°-∠AOC=60°.所以∠BOD=180°-∠AOD=120°.
小试牛刀
3
如图,直线AB 与CD 交于点O,OE⊥AB 于点O,
∠EOD∶∠DOB=3∶1,求∠COE 的度数.
小试牛刀
因为OE⊥AB,所以∠EOB=∠EOA=90°.
因为∠EOD∶∠DOB=3∶1,
所以∠DOB=90°× =22.5°.
因为∠AOC=∠DOB=22.5°,
所以∠COE=∠EOA+∠AOC
=90°+22.5°=112.5°.
解:
小试牛刀
4
已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD 的度数.
(2)如图②,若∠BOC=60°,求∠AOD 的度数.
(3)根据(1)(2)结果猜想∠AOD 与∠BOC 有怎样的关系?并
根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=
7∶29,求∠BOC 和∠AOD 的度数.
小试牛刀
(1)因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB - ∠ BOC = 90°-50°=40°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=360°-∠AOB-∠BOC-∠COD=360°-90°-60°-90°=120°.
解:
小试牛刀
(3)∠AOD 与∠BOC 互补.理由:因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-∠BOC.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互补.
(4)已知∠BOC+∠AOD=180°,又因为∠BOC :
∠AOD=7:29,所以∠BOC=35°,∠AOD=145°.
小试牛刀
5
(1)在图①中以P 为顶点画∠P,使∠P 的两边分别和∠1
的两边垂直;
(2)量一量∠P 和∠1的度数,它们之间的数量关系是
________________;
小试牛刀
(3)同样在图②和图③中以P 为顶点作∠APB,使∠APB 的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB 和∠1之间的数量关系(不要求写出理由).
图②:________________________________,
图③:________________________________;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角________(不要求写出理由).
小试牛刀
(1)如图①.
(2)量一量略;∠1+∠P=180°
(3)如图②,图③.
∠1=∠APB;
∠1=∠APB 或∠1+∠APB=180°
(4)相等或互补.
解:
课堂小结
课堂小结
以下几个方面由学生自己总结:
1.垂线的定义及垂直的符号表示;
2.垂线的有关性质;
3.过一点作已知直线的垂线的方法;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
2.1两条直线的
位置关系
第2课时
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
目录
课前导入
新课精讲
学以致用
课堂小结
课前导入
情景导入
平面内,两条直线有哪些位置关系?
复
习
回
顾
新课精讲
探索新知
1
知识点
垂直的定义
观察思考
当转动一木条的位置时,什么也随着发生了变化?
探索新知
a
b
在同一平面内,如果两条直线相交成直角,就说这两条直线互相垂直.
垂足
垂 线
垂
线
探索新知
定义:在两条直线AB 和CD 相交所成的4个角中,如果有一个角是直角,就说这两条直线互相垂直;记作“AB⊥CD ”,读作“AB 垂直于CD ”;其中一条直线叫做另一条直线的垂线,它们的交点O 叫做垂足.如图.
探索新知
导引:要判断OE,OF 是什么位置关系,其实质是说明OE,OF 是否垂直,即要看∠EOF 是否为90°;要让∠EOF=90°,需说明∠EOF=∠AOC 或∠EOF=∠BOC 都可,这样就把问题转化为说明∠AOE=∠COF (已知)了.
例1 如图,CO⊥AB 于点O,∠AOE=∠COF,则射
线OE,OF 是什么位置关系?请说明理由.
探索新知
解:射线OE,OF 互相垂直.理由如下:
因为CO⊥AB,所以∠AOC=90°.
又因为∠AOE=∠COF,
所以∠AOE+∠COE=∠COF+∠COE,
即∠AOC=∠EOF=90°.
所以OE 与OF 互相垂直(垂直定义).
探索新知
总 结
判断两直线(线段、射线所在直线)互相垂直,主要
依据是垂直定义,只要说明两条相交直线所构成的四
个角中有一个角是直角即可.
典题精讲
1
分别找出下列图中互相垂直的线段.
(1)AO⊥OC,OB⊥OD.
(2)DC⊥BC,DC⊥CE,DC⊥BE;AC⊥BC,
AC⊥CE,AC⊥BE;DA⊥BC,DA⊥CE,
DA⊥BE.
解:
典题精讲
如图,已知点O 在直线AB上,CO⊥DO 于点O,若∠1=145°,则∠3的度数为( )
A.35°
B.45°
C.55°
D.65°
2
C
典题精讲
如图,三条直线相交于点O,若CO⊥AB,∠1=56°,则∠2等于( )
A.30°
B.34°
C.45°
D.56°
3
B
典题精讲
如图,点O 在直线AB上,且OC⊥OD,若∠COA=36°,则∠DOB 的大小为( )
A.36°
B.54°
C.55°
D.44°
4
B
典题精讲
如图,已知OA⊥OB,OC⊥OD,∠AOC=27°,则∠BOD 的度数是( )
A.117°
B.127°
C.153°
D.163°
5
C
典题精讲
如图,直线AB,CD 相交于点O,射线OM 平分∠AOC,ON⊥OM.若∠AOM=35°,则∠CON 的度数为( )
A.35°
B.45°
C.55°
D.65°
6
C
探索新知
2
知识点
垂线的画法
做一做
(1)你能借助三角尺在一张白纸上
画出两条互相垂直的直线吗?
(2)如果只有直尺,你能在右图方格
纸上画出两条互相垂直的直线吗?
(3)你能用折纸的方法折出互相垂直的直线吗?试试看!
探索新知
1.垂线的画法:
经过一点(已知直线上或直线外),画已知直线的垂线,步骤如下:
(1)靠线:让直角三角板的一条直角边与已知直线重合;
(2)过点:沿直线移动,使直角三角板的另一条直角边经过已知点;
(3)画线:沿直角边画线,则这条直线就是经过这个点的已知直线的垂线.如图.
探索新知
例2
如图,M 是三角形ABC 中BC 边上的任意一点,请你按照下列要求画图:
(1)过M 点画直线AB 的垂线m;
(2)过M 点画直线BC 的垂线n;
(3)过M 点画直线AC 的垂线p.
观察图形不难看出,(1)(3)属于过直线外一点画已知
直线的垂线,(2)属于过直线上一点画已知直线的垂线,
所以按照“一靠、二过、三画”的方法画图即可.
导引:
探索新知
画出的直线m,n,p 如图.
解:
探索新知
过已知点画已知直线的垂线,实际上就是过已
知点画一条直线,使所画直线与已知直线相交所成
的角是90°.
总 结
典题精讲
1
画一条直线 l,在直线 l,上取一点A,在直线 l,外取一点B,分别经过点A,B 用三角尺或量角器画直线l 的垂线.
如图.
解:
典题精讲
2
下列选项中,过点P 画AB 的垂线,三角尺放法正确的是( )
C
典题精讲
过一条线段外一点,作这条线段的垂线,垂足在( )
A.这条线段上
B.这条线段的端点处
C.这条线段的延长线上
D.以上都有可能
3
D
探索新知
3
知识点
垂线的性质
想一想
(1)如图,点A 在直线l 上,过点A 画直线l 的垂线,你能
画出多少条?如果点A 在直线l 外呢?
A
l
A
l
探索新知
平面内,过一点有且只有一条直线与已知直线垂直.
归 纳
探索新知
例3 如图,已知直线AB,CB,l 在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
C
探索新知
导引:根据题意可知,过点B 有AB,CB 都与直线l 垂直,
由垂线的性质可知,在同一平面内,过一点有且
只有一条直线与已知直线垂直,所以A、B、C 三
点在一条直线上.
探索新知
总 结
利用直线的性质解答题目,要注意直线性质满足的条件:
1. 在平面内;
2. 过一点,点的位置可以在直线上也可以在直线外;
3. 相交所成的角必须是直角,以上三条缺一不可.
典题精讲
在同一平面内,下列语句正确的是( )
A.过一点有无数条直线与已知直线垂直
B.和一条直线垂直的直线有两条
C.过一点有且只有一条直线与已知直线垂直
D.若两直线相交,则它们一定垂直
1
C
典题精讲
如图,如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON 重合(即O,M,N 三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只
有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有
一条直线与已知直线垂直
D.两点之间,线段最短
2
C
易错提醒
(1)在图①中,过AB 外一点M 作AB 的垂线;
(2)在图②中,过点A,B 分别作OB,OA 的垂线.
易错点:误认为垂足一定要在线段或射线上而导致错误.
易错提醒
解:
(1)如图①所示.
(2)如图②所示.
学以致用
小试牛刀
已知在同一平面内:
①两条直线相交成直角;
②两条直线互相垂直;
③一条直线是另一条直线的垂线.
那么下列因果关系:①→②③;②→①③;③→①②中,正确的有( )
A.0个 B.1个 C.2个 D.3个
D
1
小试牛刀
2
在直线AB上任取一点O,过点O 作射线OC,OD,
使OC⊥OD,当∠AOC=30°时,∠BOD 的度数是多少?
小试牛刀
解:
如图①,当OC,OD 在AB 同侧时,
因为OC⊥OD,
所以∠COD=90°.
因为∠AOC=30°,
所以∠BOD=180°-∠COD-∠AOC=60°.
如图②,当OC,OD 在AB 异侧时,
因为OC⊥OD,所以∠COD=90°.
因为∠AOC=30°,所以∠AOD=90°-∠AOC=60°.所以∠BOD=180°-∠AOD=120°.
小试牛刀
3
如图,直线AB 与CD 交于点O,OE⊥AB 于点O,
∠EOD∶∠DOB=3∶1,求∠COE 的度数.
小试牛刀
因为OE⊥AB,所以∠EOB=∠EOA=90°.
因为∠EOD∶∠DOB=3∶1,
所以∠DOB=90°× =22.5°.
因为∠AOC=∠DOB=22.5°,
所以∠COE=∠EOA+∠AOC
=90°+22.5°=112.5°.
解:
小试牛刀
4
已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD 的度数.
(2)如图②,若∠BOC=60°,求∠AOD 的度数.
(3)根据(1)(2)结果猜想∠AOD 与∠BOC 有怎样的关系?并
根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=
7∶29,求∠BOC 和∠AOD 的度数.
小试牛刀
(1)因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB - ∠ BOC = 90°-50°=40°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)因为OA⊥OB,所以∠AOB=90°.因为OC⊥OD,所以∠COD=90°,所以∠AOD=360°-∠AOB-∠BOC-∠COD=360°-90°-60°-90°=120°.
解:
小试牛刀
(3)∠AOD 与∠BOC 互补.理由:因为OA⊥OB,所以∠AOB=90°,所以∠AOC=∠AOB-∠BOC=90°-∠BOC.因为OC⊥OD,所以∠COD=90°,所以∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC,所以∠AOD+∠BOC=180°,即∠AOD 与∠BOC 互补.
(4)已知∠BOC+∠AOD=180°,又因为∠BOC :
∠AOD=7:29,所以∠BOC=35°,∠AOD=145°.
小试牛刀
5
(1)在图①中以P 为顶点画∠P,使∠P 的两边分别和∠1
的两边垂直;
(2)量一量∠P 和∠1的度数,它们之间的数量关系是
________________;
小试牛刀
(3)同样在图②和图③中以P 为顶点作∠APB,使∠APB 的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB 和∠1之间的数量关系(不要求写出理由).
图②:________________________________,
图③:________________________________;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角________(不要求写出理由).
小试牛刀
(1)如图①.
(2)量一量略;∠1+∠P=180°
(3)如图②,图③.
∠1=∠APB;
∠1=∠APB 或∠1+∠APB=180°
(4)相等或互补.
解:
课堂小结
课堂小结
以下几个方面由学生自己总结:
1.垂线的定义及垂直的符号表示;
2.垂线的有关性质;
3.过一点作已知直线的垂线的方法;
同学们,
下节课见!
一键发布配套作业 & AI智能精细批改
(任务-发布任务-选择章节)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
