【新课标】24.1.1图形的旋转 课件(共31张PPT)
文档属性
| 名称 | 【新课标】24.1.1图形的旋转 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
24.1.1图形的旋转
沪科版 九年级下
教学内容分析
掌握旋转的有关概念,学会判断在图形旋转过程中的对应点、对应线段、对应角、旋转中心、旋转角。本节重点是旋转的性质。
教学目标
1.掌握旋转的有关概念,理解旋转变换也是基本图形变换之一;
2.探索和发现旋转与旋转中心、旋转角度有关,会找出旋转前后图形中的对应元素,旋转中心、旋转角;(重点)
3.根据旋转的性质,作出旋转后的图形.(难点)
核心素养分析
本节学习旋转的有关概念,在图形旋转过程中,找出对应点、对应线段、对应角、旋转中心、旋转角,学习旋转的性质,培养了学生的几何直观的核心素养,感受图形旋转的数学美。
新知导入
下面的图形用到的图形变换有哪些?
平移、轴对称
新知讲解
生活中,旋转现象普遍存在,如各种车轮子的转动,
风力发电机风叶的转动等,如图24-1.
图24-1
汽车的轮子
风力发电机的风叶
O
A'
B'
C'
A
B
C
A
B
A
B
C
θ
旋转中心
旋转角
图24-2
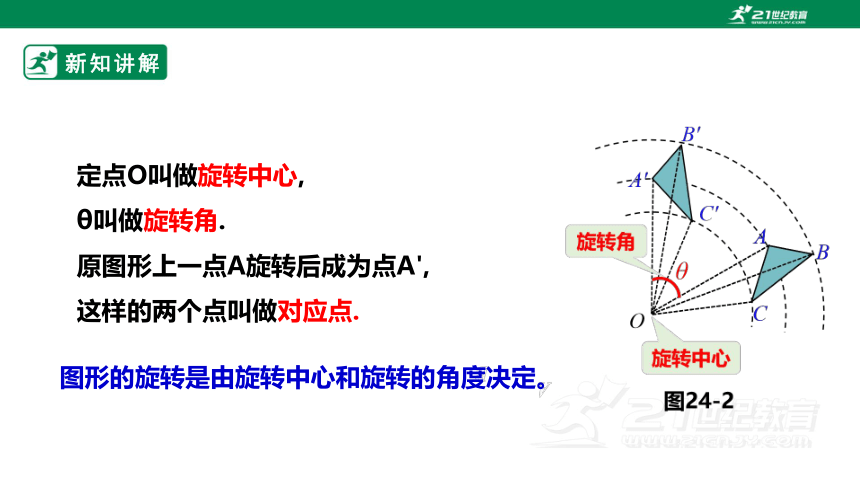
在平面内,一个图形绕着一个定点(如点O) ,旋转一定的角度(如θ),得到另一个图形的变换,叫做旋转.
新知讲解
新知讲解
定点О叫做旋转中心,
θ叫做旋转角.
原图形上一点A旋转后成为点A',
这样的两个点叫做对应点.
图形的旋转是由旋转中心和旋转的角度决定。
新知讲解
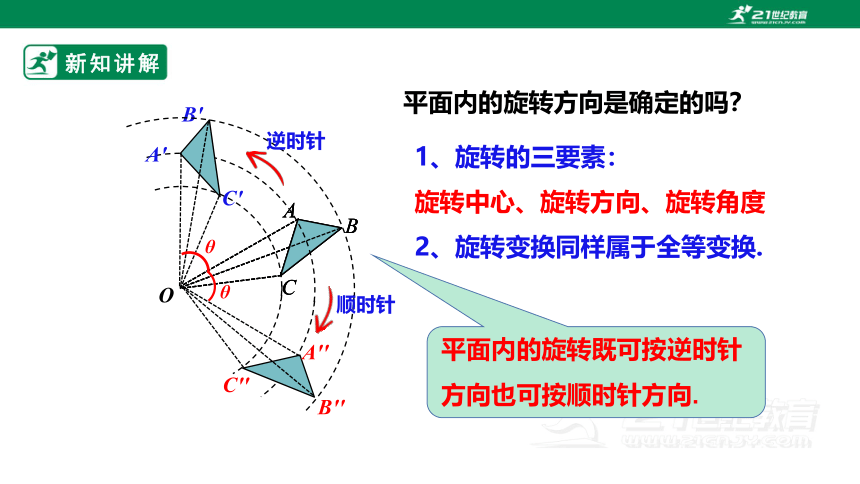
平面内的旋转既可按逆时针方向也可按顺时针方向.
A
B
C
A
B
C
A
B
C
O
A'
B'
C'
θ
A''
B''
C''
逆时针
顺时针
θ
平面内的旋转方向是确定的吗?
1、旋转的三要素:
旋转中心、旋转方向、旋转角度
2、旋转变换同样属于全等变换.
新知讲解
如图,△ABC绕着旋转中心О按逆时针方向旋转θ后,得到△A'B'C'.
(1)连接OA,OB,OC,OA',OB',OC',那么OA与OA'的长度有何关系 OB与OB’.OC与OC'也有这样的关系吗
由△ABC≌△A'B'C',△A'O'B'≌△AOB,
可得,OA=OA',OB=OB’,OC=OC'
新知讲解
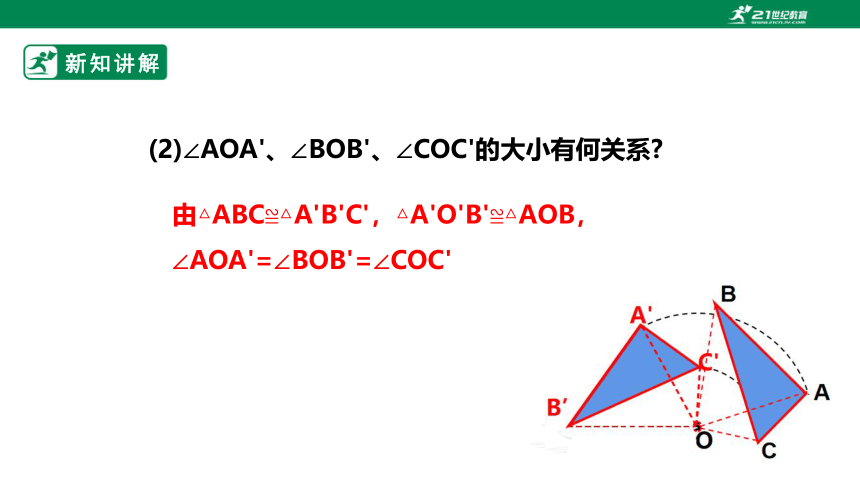
(2)∠AOA'、∠BOB'、∠COC'的大小有何关系
由△ABC≌△A'B'C',△A'O'B'≌△AOB,∠AOA'=∠BOB'=∠COC'
新知讲解
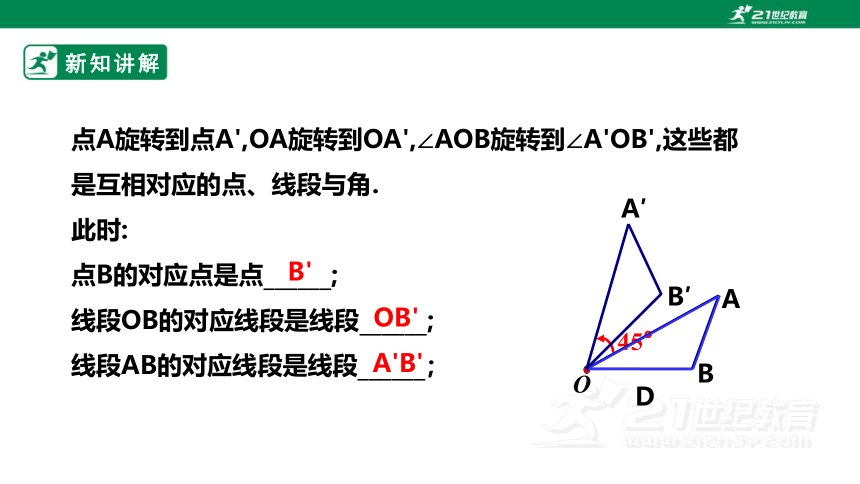
点A旋转到点A',OA旋转到OA',∠AOB旋转到∠A'OB',这些都是互相对应的点、线段与角.
此时:
点B的对应点是点______;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
45°
A′
B′
O
A
B
D
B'
OB'
A'B'
新知讲解
∠A的对应角是______;
∠B的对应角是______;
旋转中心是点_________;
旋转的角度是___________
45°
A′
B′
O
A
B
D
∠A'
∠B'
O
∠AOA'
新知讲解
在一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等;
两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
旋转中心是唯一不动的点.
新知讲解
旋转性质:
1、旋转前、后的图形全等;
2、对应点到旋转中心的距离相等;
3、每一对对应点与旋转中心的连线所成的角彼此相等。
新知讲解
在平面内,一个图形绕着一个定点旋转一定的角度θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
O
旋转中心
新知讲解
图24-3中的图形绕旋转中心旋转180°,与原图形重合;
图24-4中的图形绕旋转中心旋转120°或240°,也与原图形重合。
图24-3和图24-4中的图形都是旋转对称图形。
图24-3
图24-4
一个图形
新知讲解
45°
A′
B′
O
A
B
旋转
旋转对称图形
两个图形的变化关系
旋转和旋转对称图形有啥区别呢?
新知讲解
45°
A′
B′
O
A
B
旋转
我们学习完了平移、轴对称、旋转,它们有什么区别呢?
平移
轴对称
新知讲解
形状
大小
方向
平移
轴对称
旋转
不变
不变
不变
不变
不变
改变
不变
不变
改变
1、如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是 ( )
A. 点A与点D是对应点; B. BO=EO;
C. ∠ACB=∠FED; D. AB // DE
课堂练习
C
解:根据旋转的性质可知,
点A与点D是对应点,
BO=EO,
AB//DE,
∠ACB=∠DFE≠∠FDE.
课堂练习
课堂练习
2.如图,△ABC中,∠ACB=36°,AC=BC,将△ABC绕点A旋转到△ADE处,使DE恰好过点B,则∠CBD等于( )
A. 72° B. 60° C. 36° D. 30°
C
课堂练习
解:∵∠ACB=36°,AC=BC,
∴∠CAB=∠CBA=72°,
∵将△ABC绕点A旋转到△ADE处,
∴AB=AE,∠ABC=∠E=72°,
∴∠ABE=∠E=72°,
∴∠CBD=180°-∠ABC-∠ABE=36°,故选:C.
课堂练习
3.关于这一图案,下列说法正确的是 ( )
A. 图案乙是由甲绕BC的中点旋转180°得到的
B. 图案乙是由甲绕点C旋转108°得到的
C. 图案乙是由甲沿AB方向平移3个边长的距离得到的
D. 图案乙是由甲沿直线BC翻转180°得到的
A
课堂练习
解:如图所示:可得图案乙是由甲绕BC的中点旋转180°得到的.
故选:A.
课堂总结
旋转的性质
旋转对称图形
图形的旋转
1、旋转前、后的图形全等.
2、对应点到旋转中心的距离相等
3、每一对对应点与旋转中心的连线所成的角彼此相等.
在平面内,一个图形绕着一个定点旋转一定的角度θ (0°< θ < 360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心
板书设计
24.1.1 图形的旋转
1.旋转定义
2.旋转对称图形
作业布置
必做题:课本P3的第1~2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.1.1图形的旋转
沪科版 九年级下
教学内容分析
掌握旋转的有关概念,学会判断在图形旋转过程中的对应点、对应线段、对应角、旋转中心、旋转角。本节重点是旋转的性质。
教学目标
1.掌握旋转的有关概念,理解旋转变换也是基本图形变换之一;
2.探索和发现旋转与旋转中心、旋转角度有关,会找出旋转前后图形中的对应元素,旋转中心、旋转角;(重点)
3.根据旋转的性质,作出旋转后的图形.(难点)
核心素养分析
本节学习旋转的有关概念,在图形旋转过程中,找出对应点、对应线段、对应角、旋转中心、旋转角,学习旋转的性质,培养了学生的几何直观的核心素养,感受图形旋转的数学美。
新知导入
下面的图形用到的图形变换有哪些?
平移、轴对称
新知讲解
生活中,旋转现象普遍存在,如各种车轮子的转动,
风力发电机风叶的转动等,如图24-1.
图24-1
汽车的轮子
风力发电机的风叶
O
A'
B'
C'
A
B
C
A
B
A
B
C
θ
旋转中心
旋转角
图24-2
在平面内,一个图形绕着一个定点(如点O) ,旋转一定的角度(如θ),得到另一个图形的变换,叫做旋转.
新知讲解
新知讲解
定点О叫做旋转中心,
θ叫做旋转角.
原图形上一点A旋转后成为点A',
这样的两个点叫做对应点.
图形的旋转是由旋转中心和旋转的角度决定。
新知讲解
平面内的旋转既可按逆时针方向也可按顺时针方向.
A
B
C
A
B
C
A
B
C
O
A'
B'
C'
θ
A''
B''
C''
逆时针
顺时针
θ
平面内的旋转方向是确定的吗?
1、旋转的三要素:
旋转中心、旋转方向、旋转角度
2、旋转变换同样属于全等变换.
新知讲解
如图,△ABC绕着旋转中心О按逆时针方向旋转θ后,得到△A'B'C'.
(1)连接OA,OB,OC,OA',OB',OC',那么OA与OA'的长度有何关系 OB与OB’.OC与OC'也有这样的关系吗
由△ABC≌△A'B'C',△A'O'B'≌△AOB,
可得,OA=OA',OB=OB’,OC=OC'
新知讲解
(2)∠AOA'、∠BOB'、∠COC'的大小有何关系
由△ABC≌△A'B'C',△A'O'B'≌△AOB,∠AOA'=∠BOB'=∠COC'
新知讲解
点A旋转到点A',OA旋转到OA',∠AOB旋转到∠A'OB',这些都是互相对应的点、线段与角.
此时:
点B的对应点是点______;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
45°
A′
B′
O
A
B
D
B'
OB'
A'B'
新知讲解
∠A的对应角是______;
∠B的对应角是______;
旋转中心是点_________;
旋转的角度是___________
45°
A′
B′
O
A
B
D
∠A'
∠B'
O
∠AOA'
新知讲解
在一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等;
两组对应点分别与旋转中心的连线所成的角相等,都等于旋转角;
旋转中心是唯一不动的点.
新知讲解
旋转性质:
1、旋转前、后的图形全等;
2、对应点到旋转中心的距离相等;
3、每一对对应点与旋转中心的连线所成的角彼此相等。
新知讲解
在平面内,一个图形绕着一个定点旋转一定的角度θ(0°<θ<360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
O
旋转中心
新知讲解
图24-3中的图形绕旋转中心旋转180°,与原图形重合;
图24-4中的图形绕旋转中心旋转120°或240°,也与原图形重合。
图24-3和图24-4中的图形都是旋转对称图形。
图24-3
图24-4
一个图形
新知讲解
45°
A′
B′
O
A
B
旋转
旋转对称图形
两个图形的变化关系
旋转和旋转对称图形有啥区别呢?
新知讲解
45°
A′
B′
O
A
B
旋转
我们学习完了平移、轴对称、旋转,它们有什么区别呢?
平移
轴对称
新知讲解
形状
大小
方向
平移
轴对称
旋转
不变
不变
不变
不变
不变
改变
不变
不变
改变
1、如图,△DEF是由△ABC绕点O旋转180°得到的,则下列结论不成立的是 ( )
A. 点A与点D是对应点; B. BO=EO;
C. ∠ACB=∠FED; D. AB // DE
课堂练习
C
解:根据旋转的性质可知,
点A与点D是对应点,
BO=EO,
AB//DE,
∠ACB=∠DFE≠∠FDE.
课堂练习
课堂练习
2.如图,△ABC中,∠ACB=36°,AC=BC,将△ABC绕点A旋转到△ADE处,使DE恰好过点B,则∠CBD等于( )
A. 72° B. 60° C. 36° D. 30°
C
课堂练习
解:∵∠ACB=36°,AC=BC,
∴∠CAB=∠CBA=72°,
∵将△ABC绕点A旋转到△ADE处,
∴AB=AE,∠ABC=∠E=72°,
∴∠ABE=∠E=72°,
∴∠CBD=180°-∠ABC-∠ABE=36°,故选:C.
课堂练习
3.关于这一图案,下列说法正确的是 ( )
A. 图案乙是由甲绕BC的中点旋转180°得到的
B. 图案乙是由甲绕点C旋转108°得到的
C. 图案乙是由甲沿AB方向平移3个边长的距离得到的
D. 图案乙是由甲沿直线BC翻转180°得到的
A
课堂练习
解:如图所示:可得图案乙是由甲绕BC的中点旋转180°得到的.
故选:A.
课堂总结
旋转的性质
旋转对称图形
图形的旋转
1、旋转前、后的图形全等.
2、对应点到旋转中心的距离相等
3、每一对对应点与旋转中心的连线所成的角彼此相等.
在平面内,一个图形绕着一个定点旋转一定的角度θ (0°< θ < 360°)后,能够与原图形重合,这样的图形叫做旋转对称图形,这个定点就是旋转中心
板书设计
24.1.1 图形的旋转
1.旋转定义
2.旋转对称图形
作业布置
必做题:课本P3的第1~2题
选做题:练习册本课时的习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
