专项训练 正方形中的“三垂直”模型(含答案)
文档属性
| 名称 | 专项训练 正方形中的“三垂直”模型(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专项训练
正方形中的“三垂直”模型
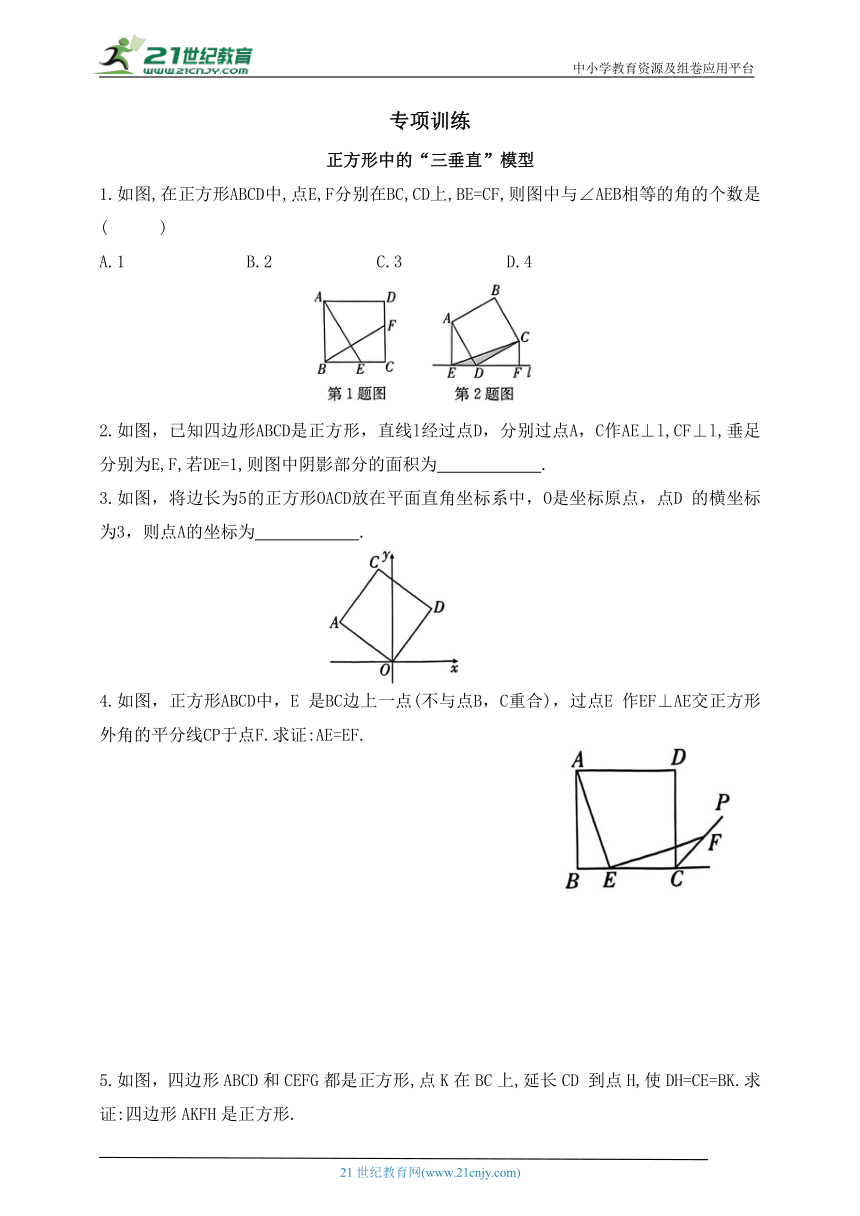
1.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
2.如图,已知四边形ABCD是正方形,直线l经过点D,分别过点A,C作AE⊥l,CF⊥l,垂足分别为E,F,若DE=1,则图中阴影部分的面积为 .
3.如图,将边长为5的正方形OACD放在平面直角坐标系中,O是坐标原点,点D 的横坐标为3,则点A的坐标为 .
4.如图,正方形ABCD中,E 是BC边上一点(不与点B,C重合),过点E 作EF⊥AE交正方形外角的平分线CP于点F.求证:AE=EF.
5.如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD 到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
6.如图,四边形ABCD是正方形,点E是边AB 上一点,延长AD至点F,使DF=BE,连接CF.
(1)求证:∠BCE=∠DCF.
(2)连接CE,过点E,F分别作CF,CE的平行线交于点G,判断四边形CEGF是什么特殊四边形,并证明.
参考答案
3.( -4,3)
4.证明:在AB上取一点G,使AG=EC,连接GE,则AB-AG=BC-EC,即BG=BE,∴∠BGE=45°,
∴∠AGE=135°.
∵CP是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AGE=∠ECF.
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,且AG=EC,∠AGE=∠ECF,
∴△AGE ≌△ECF(ASA),∴AE=EF.
5.证明:∵四边形ABCD和CEFG都是正方形,∴AB=AD =DC=BC,GC=EC=FG=EF.
∵DH=CE=BK,∴HG=EK=BC=AD=AB.
在△ADH和△ABK中,
∴∠HAD =∠BAK.
∵ ∠BAK + ∠KAD = 90°,∴∠HAD+∠KAD=90°,即∠HAK=90°.
同理可得△HGF≌△KEF≌△ABK≌△ADH,∴HF=KF=AK =AH,∴四边形AKFH是菱形.又∵∠HAK=90°,∴四边形AKFH是正方形.
6.(1)证明:∵四边形ABCD是正方形,∴∠B=∠ADC=∠BCD=90°,BC=CD,
∴∠B=∠CDF=90°.
在△BCE与△DCF中
∴∠BCE=∠DCF.
(2)解:四边形CEGF是正方形.
证明:∵EG∥CF,FG∥CE,∴四边形CEGF是平行四边形.
∵△BCE≌△DCF,∴CE=CF,∴四边形CEGF是菱形.
∵∠BCE=∠DCF,∴∠ECF=∠BCD=90°,∴四边形CEGF是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
正方形中的“三垂直”模型
1.如图,在正方形ABCD中,点E,F分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( )
A.1 B.2 C.3 D.4
2.如图,已知四边形ABCD是正方形,直线l经过点D,分别过点A,C作AE⊥l,CF⊥l,垂足分别为E,F,若DE=1,则图中阴影部分的面积为 .
3.如图,将边长为5的正方形OACD放在平面直角坐标系中,O是坐标原点,点D 的横坐标为3,则点A的坐标为 .
4.如图,正方形ABCD中,E 是BC边上一点(不与点B,C重合),过点E 作EF⊥AE交正方形外角的平分线CP于点F.求证:AE=EF.
5.如图,四边形ABCD和CEFG都是正方形,点K在BC上,延长CD 到点H,使DH=CE=BK.求证:四边形AKFH是正方形.
6.如图,四边形ABCD是正方形,点E是边AB 上一点,延长AD至点F,使DF=BE,连接CF.
(1)求证:∠BCE=∠DCF.
(2)连接CE,过点E,F分别作CF,CE的平行线交于点G,判断四边形CEGF是什么特殊四边形,并证明.
参考答案
3.( -4,3)
4.证明:在AB上取一点G,使AG=EC,连接GE,则AB-AG=BC-EC,即BG=BE,∴∠BGE=45°,
∴∠AGE=135°.
∵CP是外角平分线,∴∠DCF=45°,∴∠ECF=135°,∴∠AGE=∠ECF.
∵∠AEB+∠BAE=90°,∠AEB+∠CEF=90°,∴∠BAE=∠CEF,且AG=EC,∠AGE=∠ECF,
∴△AGE ≌△ECF(ASA),∴AE=EF.
5.证明:∵四边形ABCD和CEFG都是正方形,∴AB=AD =DC=BC,GC=EC=FG=EF.
∵DH=CE=BK,∴HG=EK=BC=AD=AB.
在△ADH和△ABK中,
∴∠HAD =∠BAK.
∵ ∠BAK + ∠KAD = 90°,∴∠HAD+∠KAD=90°,即∠HAK=90°.
同理可得△HGF≌△KEF≌△ABK≌△ADH,∴HF=KF=AK =AH,∴四边形AKFH是菱形.又∵∠HAK=90°,∴四边形AKFH是正方形.
6.(1)证明:∵四边形ABCD是正方形,∴∠B=∠ADC=∠BCD=90°,BC=CD,
∴∠B=∠CDF=90°.
在△BCE与△DCF中
∴∠BCE=∠DCF.
(2)解:四边形CEGF是正方形.
证明:∵EG∥CF,FG∥CE,∴四边形CEGF是平行四边形.
∵△BCE≌△DCF,∴CE=CF,∴四边形CEGF是菱形.
∵∠BCE=∠DCF,∴∠ECF=∠BCD=90°,∴四边形CEGF是正方形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
