专项训练 特殊四边形中的折叠问题(含答案)
文档属性
| 名称 | 专项训练 特殊四边形中的折叠问题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 12:46:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
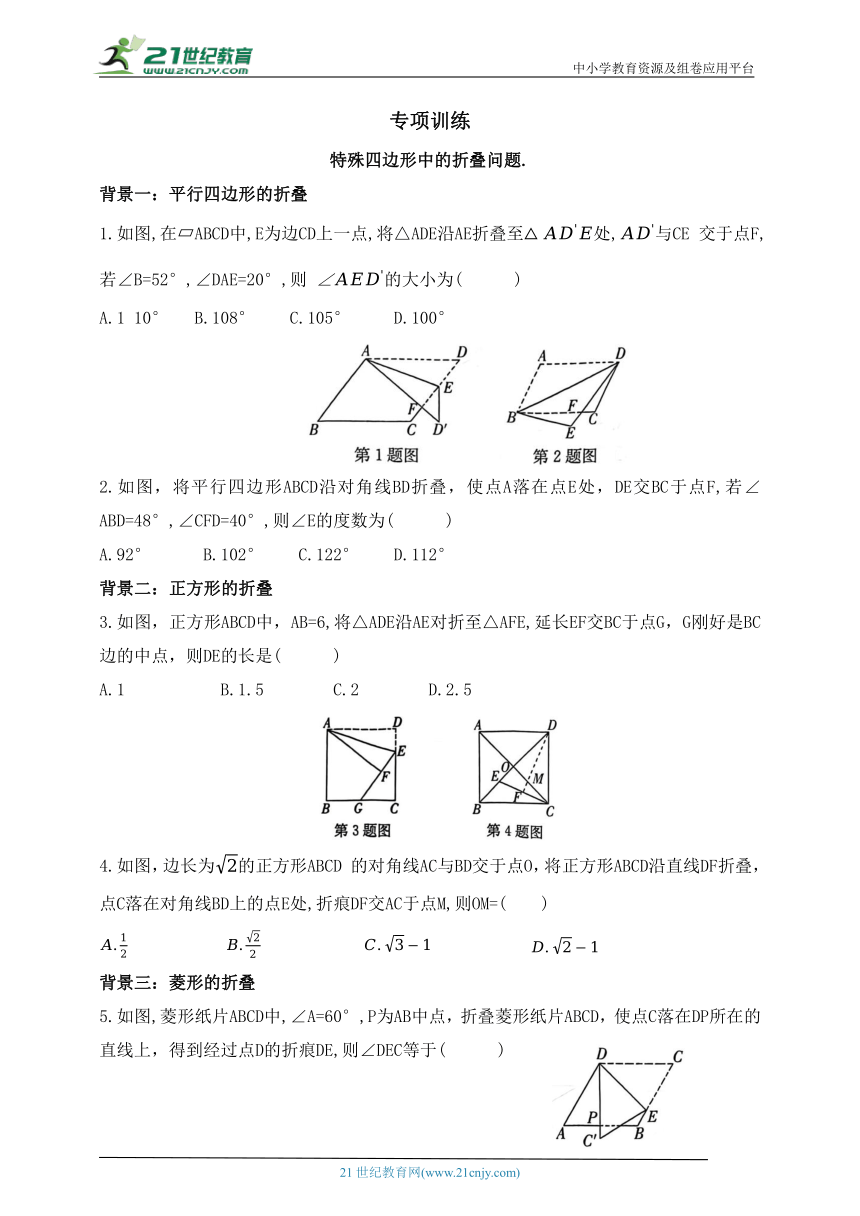
特殊四边形中的折叠问题.
背景一:平行四边形的折叠
1.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至处,与CE 交于点F,若∠B=52°,∠DAE=20°,则 的大小为( )
A.1 10° B.108° C.105° D.100°
2.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,DE交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E的度数为( )
A.92° B.102° C.122° D.112°
背景二:正方形的折叠
3.如图,正方形ABCD中,AB=6,将△ADE沿AE对折至△AFE,延长EF交BC于点G,G刚好是BC边的中点,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
4.如图,边长为的正方形ABCD 的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM=( )
背景三:菱形的折叠
5.如图,菱形纸片ABCD中,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于( )
A.60° B.65° C.75° D.80°
背景四:矩形的折叠
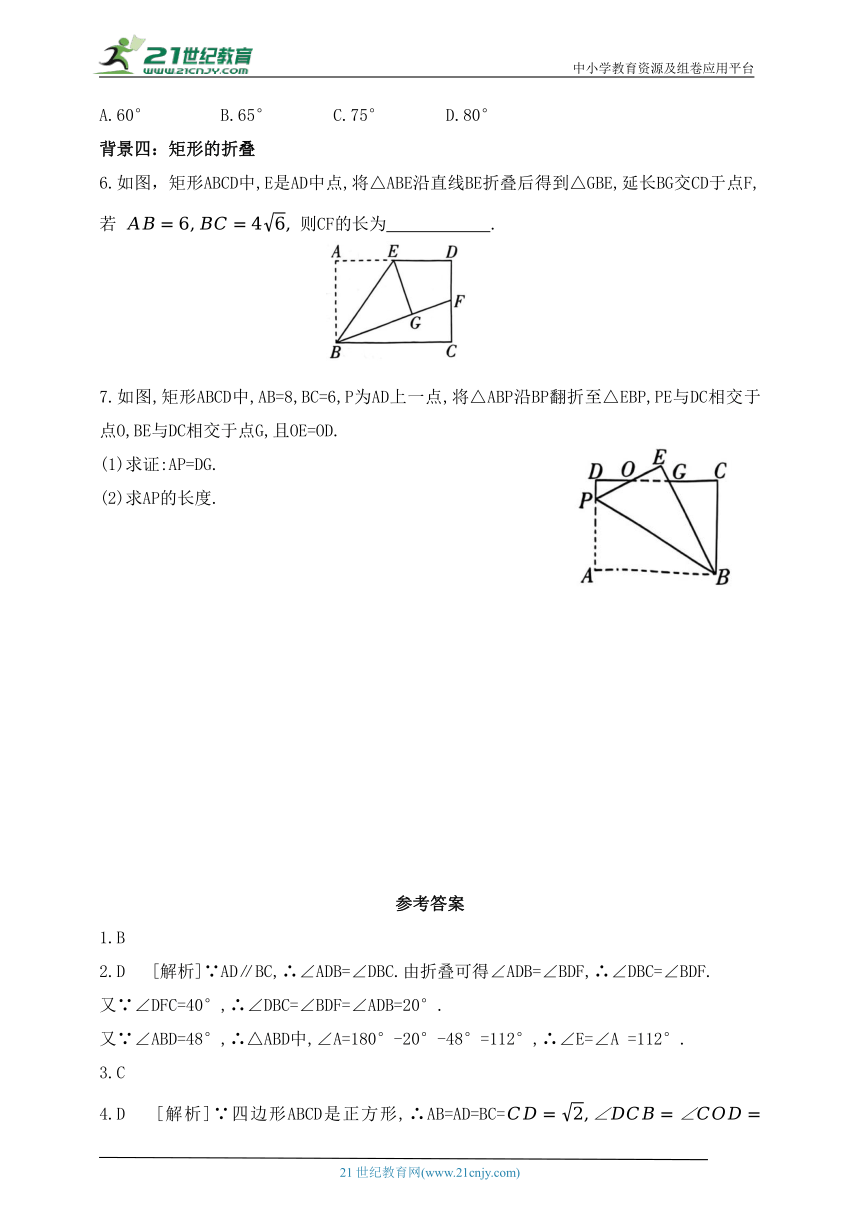
6.如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若 则CF的长为 .
7.如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与DC相交于点O,BE与DC相交于点G,且OE=OD.
(1)求证:AP=DG.
(2)求AP的长度.
参考答案
1.B
2.D [解析]∵AD∥BC,∴∠ADB=∠DBC.由折叠可得∠ADB=∠BDF,∴∠DBC=∠BDF.
又∵∠DFC=40°,∴∠DBC=∠BDF=∠ADB=20°.
又∵∠ABD=48°,∴△ABD中,∠A=180°-20°-48°=112°,∴∠E=∠A =112°.
3.C
4.D [解析]∵四边形ABCD是正方形,∴AB=AD=BC=
∵将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,
∠FED=∠ECO+∠OEC=90°,
∴∠ODM=∠OCE.
在△OEC与△OMD中
5.C [解析]连接BD.
∵四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°.
∵P 为AB的中点,∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
∴在△DEC中,∠DEC=180°-(∠CDE+∠C)=75°.
6.2 [解析]连接EF.∵E是AD的中点,∴AE=DE.
∵△ABE沿BE折叠后得到△GBE,∴AE=EG,AB=
∵在矩形ABCD中,∠A=∠D=90°,∴∠EGF=90°.∵ED=EG,EF=EF,
∴Rt△EDF ≌Rt△EGF(HL),∴DF=FG.
设DF=x,则BF=6+x,CF=6-x.
在Rt△BCF中, 解得x=4,∴CF=2.
7.(1)证明:∵四边形ABCD是矩形,∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.
根据题意得△ABP≌△EBP,∴EP=AP,∠E=∠A=90°,BE=AB=8,∴∠E=∠D.
∵OE=OD,∠GOE=∠POD,∴△ODP≌△OEG(ASA),∴PD=GE,OP=OG.
∵OE=OD,∴OE +OP=OD+OG,即EP=DG,∴AP=DG.
(2)解:由(1)得△ODP≌△OEG,∴PD=GE.
又∵DG=EP,∴设AP=EP=x,则PD=GE=6-x,DG=x,∴CG=8-x,BG=8-(6-x)=2+x.
在Rt△BCG中,根据勾股定理得BC +CG =BG ,
即6 +(8-x) =(x+2) , 解得x =4.8,∴AP=4.8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
特殊四边形中的折叠问题.
背景一:平行四边形的折叠
1.如图,在 ABCD中,E为边CD上一点,将△ADE沿AE折叠至处,与CE 交于点F,若∠B=52°,∠DAE=20°,则 的大小为( )
A.1 10° B.108° C.105° D.100°
2.如图,将平行四边形ABCD沿对角线BD折叠,使点A落在点E处,DE交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E的度数为( )
A.92° B.102° C.122° D.112°
背景二:正方形的折叠
3.如图,正方形ABCD中,AB=6,将△ADE沿AE对折至△AFE,延长EF交BC于点G,G刚好是BC边的中点,则DE的长是( )
A.1 B.1.5 C.2 D.2.5
4.如图,边长为的正方形ABCD 的对角线AC与BD交于点O,将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM=( )
背景三:菱形的折叠
5.如图,菱形纸片ABCD中,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于( )
A.60° B.65° C.75° D.80°
背景四:矩形的折叠
6.如图,矩形ABCD中,E是AD中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F,若 则CF的长为 .
7.如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与DC相交于点O,BE与DC相交于点G,且OE=OD.
(1)求证:AP=DG.
(2)求AP的长度.
参考答案
1.B
2.D [解析]∵AD∥BC,∴∠ADB=∠DBC.由折叠可得∠ADB=∠BDF,∴∠DBC=∠BDF.
又∵∠DFC=40°,∴∠DBC=∠BDF=∠ADB=20°.
又∵∠ABD=48°,∴△ABD中,∠A=180°-20°-48°=112°,∴∠E=∠A =112°.
3.C
4.D [解析]∵四边形ABCD是正方形,∴AB=AD=BC=
∵将正方形ABCD沿直线DF折叠,点C落在对角线BD上的点E处,
∠FED=∠ECO+∠OEC=90°,
∴∠ODM=∠OCE.
在△OEC与△OMD中
5.C [解析]连接BD.
∵四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°.
∵P 为AB的中点,∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,∴∠PDC=90°,
∴由折叠的性质得到∠CDE=∠PDE=45°,
∴在△DEC中,∠DEC=180°-(∠CDE+∠C)=75°.
6.2 [解析]连接EF.∵E是AD的中点,∴AE=DE.
∵△ABE沿BE折叠后得到△GBE,∴AE=EG,AB=
∵在矩形ABCD中,∠A=∠D=90°,∴∠EGF=90°.∵ED=EG,EF=EF,
∴Rt△EDF ≌Rt△EGF(HL),∴DF=FG.
设DF=x,则BF=6+x,CF=6-x.
在Rt△BCF中, 解得x=4,∴CF=2.
7.(1)证明:∵四边形ABCD是矩形,∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8.
根据题意得△ABP≌△EBP,∴EP=AP,∠E=∠A=90°,BE=AB=8,∴∠E=∠D.
∵OE=OD,∠GOE=∠POD,∴△ODP≌△OEG(ASA),∴PD=GE,OP=OG.
∵OE=OD,∴OE +OP=OD+OG,即EP=DG,∴AP=DG.
(2)解:由(1)得△ODP≌△OEG,∴PD=GE.
又∵DG=EP,∴设AP=EP=x,则PD=GE=6-x,DG=x,∴CG=8-x,BG=8-(6-x)=2+x.
在Rt△BCG中,根据勾股定理得BC +CG =BG ,
即6 +(8-x) =(x+2) , 解得x =4.8,∴AP=4.8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
