第六章 特殊平行四边形 章末复习(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 章末复习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
章末复习
考点整合
考点一:菱形的性质与判定
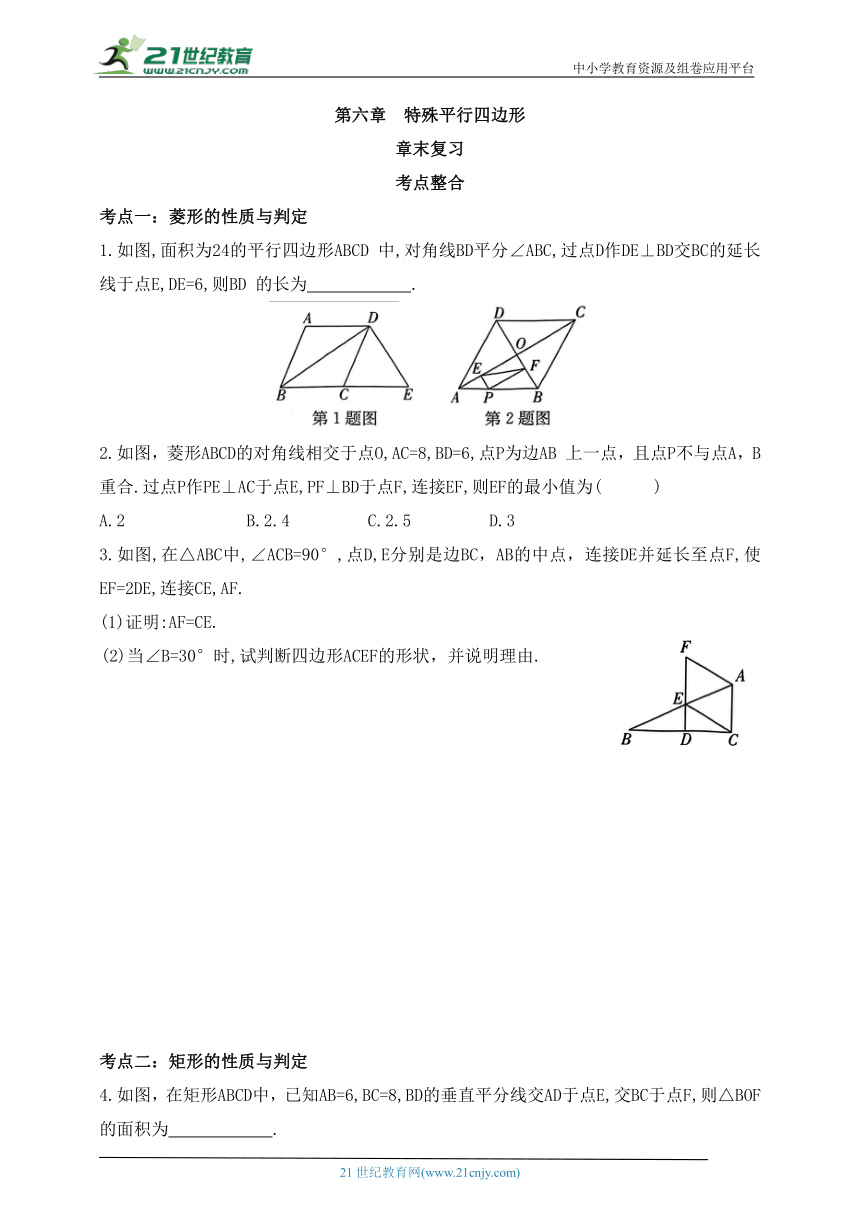
1.如图,面积为24的平行四边形ABCD 中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则BD 的长为 .
2.如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,点P为边AB 上一点,且点P不与点A,B重合.过点P作PE⊥AC于点E,PF⊥BD于点F,连接EF,则EF的最小值为( )
A.2 B.2.4 C.2.5 D.3
3.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.
(1)证明:AF=CE.
(2)当∠B=30°时,试判断四边形ACEF的形状,并说明理由.
考点二:矩形的性质与判定
4.如图,在矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则△BOF的面积为 .
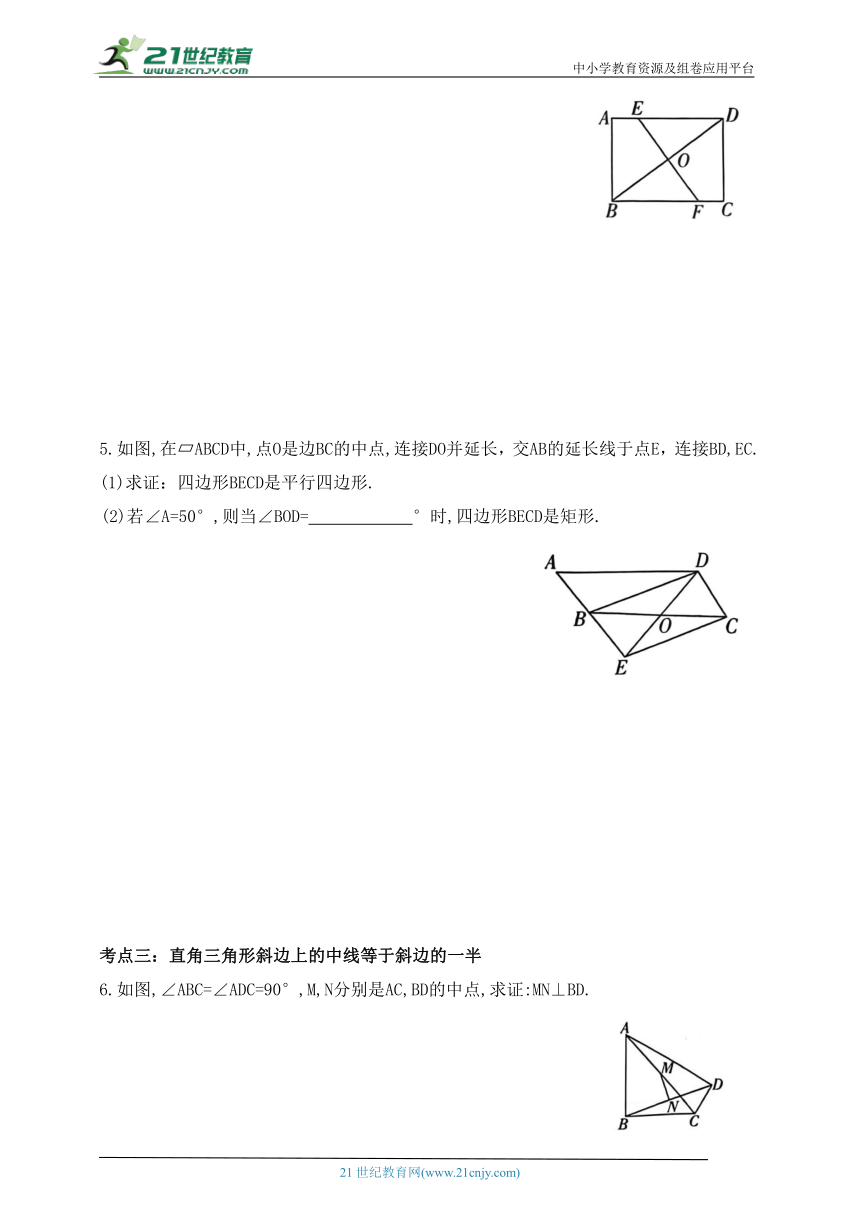
5.如图,在 ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形.
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.
考点三:直角三角形斜边上的中线等于斜边的一半
6.如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,求证:MN⊥BD.
考点四:正方形的性质与判定
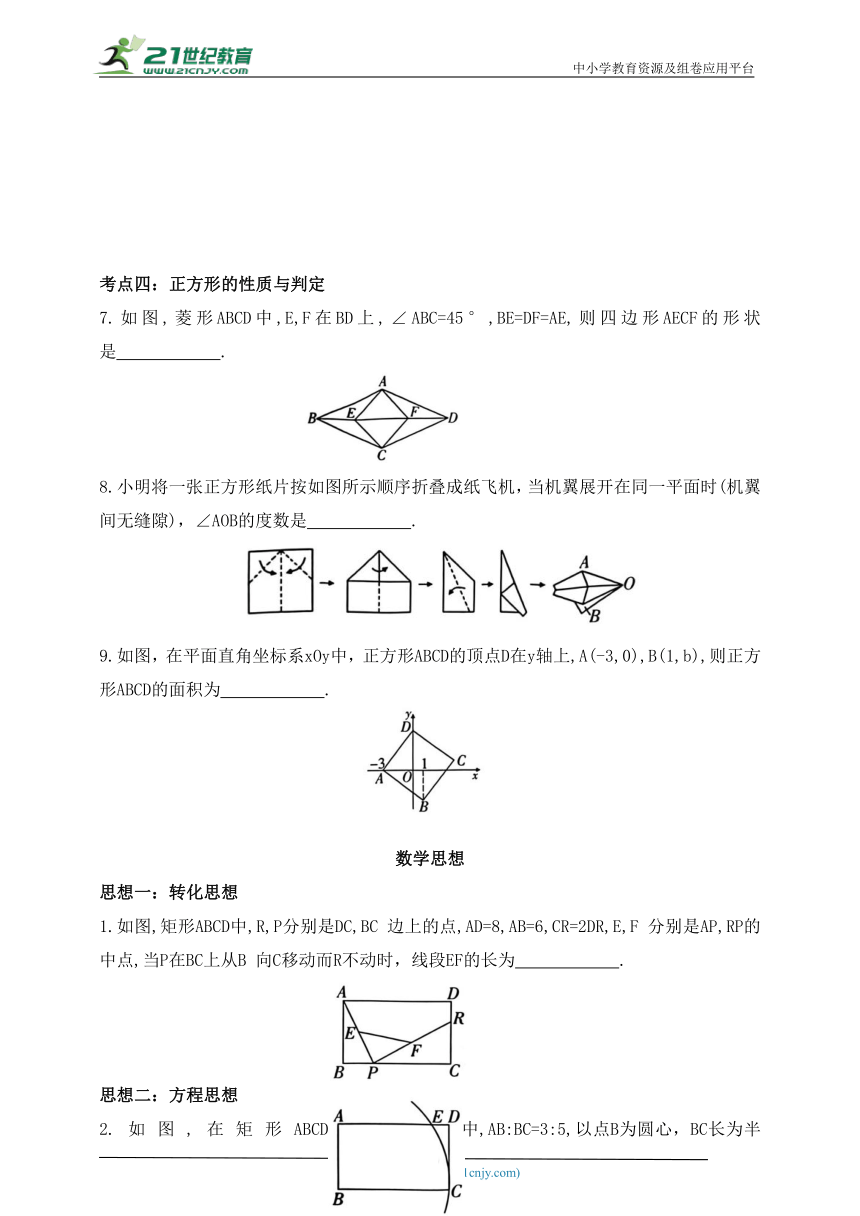
7.如图,菱形ABCD中,E,F在BD上,∠ABC=45°,BE=DF=AE,则四边形AECF的形状是 .
8.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是 .
9.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(-3,0),B(1,b),则正方形ABCD的面积为 .
数学思想
思想一:转化思想
1.如图,矩形ABCD中,R,P分别是DC,BC 边上的点,AD=8,AB=6,CR=2DR,E,F 分别是AP,RP的中点,当P在BC上从B 向C移动而R不动时,线段EF的长为 .
思想二:方程思想
2.如图,在矩形ABCD中,AB:BC=3:5,以点B为圆心,BC长为半径作圆弧,与边AD 交于点E,则
思想三:分类讨论思想
3.如图,在矩形ABCD中,AB=3,BC=4.M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN.
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
参考答案
考点整合
1.8 2.B
3.(1)证明:∵点D,E分别是边BC,AB的中点,∴DE∥AC,AC=2DE.∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE.
(2)解:当∠B=30°时,四边形ACEF是菱形.
理由:∵∠ACB=90°,∠B= 是等边三角形,
∴AC=CE.
又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.
5.(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC,AB =CD,∴∠OEB=∠ODC.
又∵O为BC的中点,∴BO=CO.
在△BOE和△COD中 ≌△COD(AAS),
∴OE=OD,∴四边形BECD是平行四边形.
(2)100
6.证明:如图,连接BM,DM.
∵∠ABC=∠ADC=90°,M是AC的中点,
∵点N是BD的中点,∴MN⊥BD.
7.正方形 8.45° 9.25
数学思想
3.(1)证明:∵四边形ABCD是矩形,∴AB=CD,AB∥CD,∴∠MAB= ∠NCD.
在△ABM 和△CDN 中,
(2)解:如图,连接EF,交AC于点O.
∵四边形ABCD是矩形,∴AD∥BC,∴∠EAO=∠FCO.
在△AEO和△CFO中 =FO,AO=CO,
∴O为EF,AC的中点.
∵∠EGF=90°,
∴在Rt△ABC中,
或AG=OA+OG=4,∴AG的长为1或4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
章末复习
考点整合
考点一:菱形的性质与判定
1.如图,面积为24的平行四边形ABCD 中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则BD 的长为 .
2.如图,菱形ABCD的对角线相交于点O,AC=8,BD=6,点P为边AB 上一点,且点P不与点A,B重合.过点P作PE⊥AC于点E,PF⊥BD于点F,连接EF,则EF的最小值为( )
A.2 B.2.4 C.2.5 D.3
3.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB的中点,连接DE并延长至点F,使EF=2DE,连接CE,AF.
(1)证明:AF=CE.
(2)当∠B=30°时,试判断四边形ACEF的形状,并说明理由.
考点二:矩形的性质与判定
4.如图,在矩形ABCD中,已知AB=6,BC=8,BD的垂直平分线交AD于点E,交BC于点F,则△BOF的面积为 .
5.如图,在 ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形.
(2)若∠A=50°,则当∠BOD= °时,四边形BECD是矩形.
考点三:直角三角形斜边上的中线等于斜边的一半
6.如图,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点,求证:MN⊥BD.
考点四:正方形的性质与判定
7.如图,菱形ABCD中,E,F在BD上,∠ABC=45°,BE=DF=AE,则四边形AECF的形状是 .
8.小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙),∠AOB的度数是 .
9.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,A(-3,0),B(1,b),则正方形ABCD的面积为 .
数学思想
思想一:转化思想
1.如图,矩形ABCD中,R,P分别是DC,BC 边上的点,AD=8,AB=6,CR=2DR,E,F 分别是AP,RP的中点,当P在BC上从B 向C移动而R不动时,线段EF的长为 .
思想二:方程思想
2.如图,在矩形ABCD中,AB:BC=3:5,以点B为圆心,BC长为半径作圆弧,与边AD 交于点E,则
思想三:分类讨论思想
3.如图,在矩形ABCD中,AB=3,BC=4.M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN.
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
参考答案
考点整合
1.8 2.B
3.(1)证明:∵点D,E分别是边BC,AB的中点,∴DE∥AC,AC=2DE.∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE.
(2)解:当∠B=30°时,四边形ACEF是菱形.
理由:∵∠ACB=90°,∠B= 是等边三角形,
∴AC=CE.
又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.
5.(1)证明:∵四边形ABCD为平行四边形,∴AB∥DC,AB =CD,∴∠OEB=∠ODC.
又∵O为BC的中点,∴BO=CO.
在△BOE和△COD中 ≌△COD(AAS),
∴OE=OD,∴四边形BECD是平行四边形.
(2)100
6.证明:如图,连接BM,DM.
∵∠ABC=∠ADC=90°,M是AC的中点,
∵点N是BD的中点,∴MN⊥BD.
7.正方形 8.45° 9.25
数学思想
3.(1)证明:∵四边形ABCD是矩形,∴AB=CD,AB∥CD,∴∠MAB= ∠NCD.
在△ABM 和△CDN 中,
(2)解:如图,连接EF,交AC于点O.
∵四边形ABCD是矩形,∴AD∥BC,∴∠EAO=∠FCO.
在△AEO和△CFO中 =FO,AO=CO,
∴O为EF,AC的中点.
∵∠EGF=90°,
∴在Rt△ABC中,
或AG=OA+OG=4,∴AG的长为1或4.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
